新高考新理念 新题型新视野——结构不良试题的研究

姜竹岭 (西安交通大学苏州附属中学 215000)

江苏高考2008方案走过了12年的历程，于2020年画上了句号．2021年起江苏高考将进入新高考模式．本文将对新高考2020年山东数学卷的新题型进行讨论，为江苏同行的高三数学复习提供参考．

1 新高考题型的变化及价值

在2020年新高考的山东卷中，出现如下的试题(10分)：

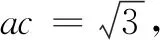
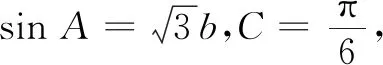
此题虽然难度不大，但与以往的考题却大不相同．以往的考题都是初始、目标状态和算子都非常明确的试题，这里的算子是指解决问题的途径和方法．也就是说传统的考试试题都是结构良好的封闭题．而新高考山东卷的第17题，题目的条件需要考生自己补充完善，题目的结论需要自己探究．这是一种新的题型，也是贯彻课标理念的一种尝试．

《普通高中数学课程标准(2017年版)》提出了“四基四能”，其中的“四能”是发现、提出、分析、解决问题的能力．2020年山东卷第17题要求学生自己补充条件，然后再解决自己提出的问题，这是贯彻“四能”的一种尝试，标志着新高考将紧贴课标理念，凸显素养的考查，从传统的能力立意转向素养导向．

与传统的结构良好的封闭题不同，我们把初始状态、目标状态和算子这三者中至少有一个没有明确界定的问题称为结构不良问题．[1]

2 结构不良题的讨论及其教育价值

结构不良问题最早来自于认知心理学，早在1965年，Reitman就从认知心理学的角度区分了结构良好问题和结构不良问题．其实生活中的很多问题，包括历史上一些有趣的问题，都是结构不良问题．譬如古印度有这样一个问题：

古印度有一位老人，临终前留下遗嘱，要把11头牛分给三个儿子，老大分得总数的二分之一，老二分得总数的四分之一，老三分得总数的六分之一．按印度的教规，牛被视为神灵，不能宰杀，只能整头分，三兄弟一筹莫展，你能帮助他们解决问题吗？

2020年山东高考数学第17题和上述定义的结构不良题相比也不完全相同．第17题是在限定的三个条件中选一个，补充题目的条件，原题就变成一个结构良好的封闭题．这种题型有一定的开放性，但开放度非常有限．所以我们把这种题称为半结构不良题更为合适．

值得指出的是，即使是以这样的半结构不良题作为试题，也是高考历史上的一大突破．虽然此题难度不大，但要求学生通盘考虑所给的三个条件，对给出的三个条件进行预判，选出最利于解决问题的那个条件．这种要求学生先分析后选择的试题，考查了学生对数学本质的理解和对数学问题的洞察力，从而真正考查了学生内在的数学素养．因此，这种结构不良的试题对学生的要求更高，要求学生有扎实的数学基础、严谨的科学思维及科学的探究能力．

在学生已有的学习生涯中，几乎所有的试题都是结构良好的，其条件不多不少，问题明确，思路和解法规范，学生已经适应这种类型的试题．而结构不良试题由于其条件模糊、解决问题的思路和方案多样、试题结果开放等特点，在学生解决问题的过程中，能有效地激发学生学习的求知欲，帮助学生从多个方面去把握问题的本质，追求试题知识蕴含的价值，有效形成跨学科综合解决问题的能力．因此，结构不良试题对促进学生的素养养成和学习能力的提升具有重要意义．

3 结构不良试题的编制

综合目前高考试题和各个地方的模考题，数学学科的结构不良试题主要体现在以下几个方面：(1)题目的条件缺失或多选一；(2)题目的问题目标不明确；(3)题目的解决方法或途径具有多样性；(4)题目中所涉及的概念和原理等不明确；(5)问题解决方法的评价标准具有多样性．

本文从题目的条件缺失或多选一这一方面对结构不良试题进行研究，探究如何把传统的结构良好试题改编为结构不良试题及结构不良试题中的条件形成的来龙去脉，帮助学生揭开结构不良试题的神秘面纱，打消对结构不良试题的恐慌．

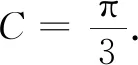
本题结构完整，属于常规题，学生对题目较熟悉，只需把题目所给的每一个条件加以理解和转化，解决起来比较容易．而新高考对于结构不良试题的考查要求之一是题目的条件缺失或者冗余，因此需要对题目的条件加以变动，使题目变得开放起来，这也有助于学生的发散性思维和探究能力的培养．因此，在改编本题时，可以对题目的某一个条件加以改动，从不同的知识层面对其进行转化，得到多个等价的条件，再从等价的条件中任选三个出来，便可呈现出一道开放性的试题．

·利用正、余弦定理进行转化

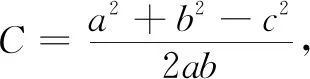
·利用角的函数值进行转化

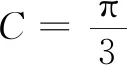
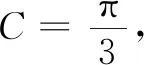
对于2cosC=1，若两边同时乘以sinA，得到2sinAcosC=sinA，两边同时加上2cosAsinC，则得到2sinAcosC+2cosAsinC=sinA+2cosAsinC，即2sin(A+C)=sinA+2cosAsinC，即2sinB=sinA+2cosAsinC．若进一步再用正弦定理，则得到2b-a=2ccosA．

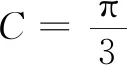
·利用三角形中的射影定理进行转化

在△ABC中，记角A,B,C所对的边分别为a,b,c，过C作边AB的垂线，垂足为D．在△ACD中，AD=bcosA．在△BCD中，BD=acosB，则c=AD+BD=acosB+bcosA．此时在2cosC=1的两边同时乘以c得到2ccosC=c，即得到2ccosC=acosB+bcosA．同理得到2bcosC=acosC+ccosA和2acosC=ccosB+bcosC．

·利用向量的数量积和三角形面积进行转化

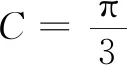
4 试题呈现

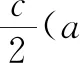
已知△ABC的内角A,B,C所对的边分别为a,b,c，且．

(1)求角C；

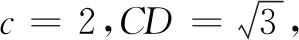
(注：如果选择多个条件分别解答，按第一个解答计分)

5 结语

中国高考正在实现从能力立意到素养导向的历史性转变，而结构不良试题的出现正体现着素养导向的高考数学命题方向，需要学生根据具体的问题情境，多层面多角度地对试题进行分析，考虑可能出现的多种情况，寻找不同的解题思路，给出不同的解决方法．这要求学生对题中给出的条件有预判能力，选出最合适的条件，短时间内给出准确的答案，以此考查学生数学思维的发散性、灵活性、创造性、严谨性．在目前的高考中，结构不良试题可能会涉及解三角形、数列、立体几何等内容，教师应在原有的结构良好试题的基础上，组织学生一起对试题进行学习和探究，领会试题所蕴含的知识，对试题中的条件和问题进行多角度多层面的转化，尝试改编成一些结构不良的试题．学生在对知识理解掌握的同时，也会收获成功改编试题的喜悦，提升学习数学的兴趣.这一尝试同时也有助于培养学生数学探究的能力和严谨的科学态度，实现立德树人的教育目标．