Robust Optimization-Based Iterative Learning Control for Nonlinear Systems With Nonrepetitive Uncertainties
2021-04-13DeyuanMengSeniorMemberIEEEandJingyaoZhang
Deyuan Meng, Senior Member, IEEE and Jingyao Zhang
Abstract—This paper aims to solve the robust iterative learning control (ILC) problems for nonlinear time-varying systems in the presence of nonrepetitive uncertainties. A new optimization-based method is proposed to design and analyze adaptive ILC, for which robust convergence analysis via a contraction mapping approach is realized by leveraging properties of substochastic matrices. It is shown that robust tracking tasks can be realized for optimization-based adaptive ILC, where the boundedness of system trajectories and estimated parameters can be ensured,regardless of unknown time-varying nonlinearities and nonrepetitive uncertainties. Two simulation tests, especially implemented for an injection molding process, demonstrate the effectiveness of our robust optimization-based ILC results.
I. INTRODUCTION
INTELLIGENT control has generated considerable research interest in both theories and applications of linear/nonlinear systems, where of particular note are the learning-based design methods (see, e.g., [1]–[5]). As a class of effective intelligent control methods with the specific focus on realizing the perfect tracking tasks for the systems that are repetitively executed, iterative learning control (ILC) has been considered as one of the most practically important learning-based design methods in many application fields, see, e.g., [6] for multiaxis robots, [7] for micro aerial vehicles, [8] for linear motor positioning systems, [9] for high-speed trains, and [10] for Chylla-Haase reactors. The readers are referred to the detailed explanations that have been introduced for characteristics and applications of ILC in the surveys of, e.g., [11]–[13]. In particular, ILC has been regarded as one of the most famous and applicable data-driven control methods [14]–[18] that may be alternatively called the model-free control methods[19]–[21], where the accurate models are generally not needed for the ILC algorithm design as well as convergence analysis.Typically, this class of data-driven ILC methods are explored based on an optimization issue that focuses directly on nonlinear systems, regardless of unknown nonlinearities.
In addition to the tight relation to optimization-based design, the data-driven ILC employs a dynamical linearization approach to overcome unknown nonlinearities and an adaptive approach to estimate linearization parameters [15]–[21]. This yields a class of optimization-based adaptive ILC methods that are capable of accommodating unknown dynamics in both nonlinear systems and their dynamical linearization models.For the convergence analysis, optimization-based adaptive ILC adopts a contraction mapping (CM)-based approach that is usually implemented via the eigenvalue analysis. Though it is popularly applied in ILC, the eigenvalue-based CM approach requires ILC processes to have iteration-independent parameters from the perspective of standard linear system theory [22], [23].
It is worth emphasizing that for nonlinear control plants, the dynamical linearization inevitably leads to iteration-dependent model parameters [15]–[21]. This renders the eigenvaluebased CM approach no longer effective in implementing convergence analysis of optimization-based adaptive ILC.Another issue left to settle for optimization-based adaptive ILC is robustness with regard to iteration-dependent uncertainties that are considered to be practically important for ILC [24]–[31]. Actually, the robust issue has not been well studied for optimization-based adaptive ILC (see, e.g.,[15]–[21]). It is mainly due to that the iteration-dependent uncertainties may bring challenging difficulties into ILC convergence in the presence of nonrepetitiveness created by iteration-dependent model parameters. To accommodate the effects arising from nonrepetitiveness, new design and analysis approaches for ILC usually need to be explored, see,e.g., [18] for an extended state observer-based design approach and [24], [28] for a double-dynamics analysis(DDA) approach. Despite these new approaches, the eigenvalue analysis is still leveraged in [18], and linear systems are only considered in [24], [28].
In this paper, we are devoted to exploring the robust problem of optimization-based adaptive ILC that is subject to unknown time-varying nonlinearities and nonrepetitive uncertainties due to iteration-dependent initial shifts and disturbances. The main contributions of our established design and analysis results are specified as follows.
1) We propose a new optimization-based design method for adaptive ILC. This new design method makes it feasible to directly apply the CM-based analysis approach of ILC to develop the boundedness of estimated parameters that are used in our adaptive updating law for the estimation of unknown time-varying nonlinearities.
2) We introduce a new robust convergence analysis method for optimization-based adaptive ILC by implementing a DDA approach and resorting to the use of the properties of the substochastic matrices. This makes it possible to not only accomplish the robust convergence analysis of optimizationbased adaptive ILC, but also guarantee the boundedness of all the system trajectories.
3) Our design methods and analysis results of optimizationbased adaptive ILC can effectively work, regardless of the presence of nonrepetitive uncertainties. This particularly helps to overcome the drawbacks of those methods and results for optimization-based adaptive ILC established through applying the eigenvalue-based CM approach in, e.g., [16], [17].
In addition, we demonstrate the robust performance of our proposed optimization-based adaptive ILC with two simulation examples, regardless of the initial shifts and disturbances that are varying with respect to both iteration and time.
The rest of our paper is organized as follows. In Section II,a robust tracking problem of optimization-based ILC is given.In Section III, an optimization-based adaptive ILC is accordingly proposed, and the main design and analysis results are derived. Simulation tests and concluding remarks are made in Sections IV and V, respectively.



III. MAIN RESULTS
A. Design of Optimization-Based Adaptive ILC
We design optimization-based adaptive ILC to overcome the effect of unknown nonlinear time-varying dynamics on seeking output tracking objectives for (1), regardless of the presence of nonrepetitive uncertainties. Towards this end, we establish the following lemma to derive an extended dynamical linearization for the unknown nonlinear timevarying dynamics of (1).
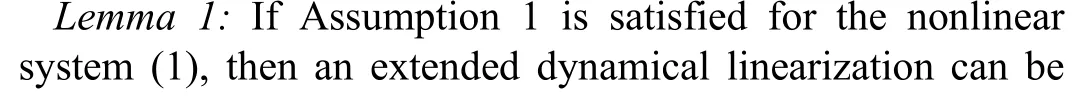



B. Robust Convergence Analyses of ILC

Next, the robust convergence analysis of optimization-based adaptive ILC for the nonlinear system (1) is explored.Towards this end, the dynamics of the tracking error are considered, and by combining (15) with (14), it can be verified that analysis not applicable any longer for developing the ILC convergence based on (20). By such observation, we leverage the properties of substochastic matrices to develop a CMbased approach for the ILC convergence analysis, together with combining a DDA approach to the optimization-based adaptive ILC.










IV. SIMULATION TESTS
To illustrate the effectiveness of the proposed optimizationbased adaptive ILC, we perform simulation tests by considering a numerical example and an injection molding process.
Example 1: Consider the nonlinear system (1) with


TABLE I PARAMETERS USED IN (15), S1) AND S2)

Example 2: Consider an injection molding process, devoting to the dynamics between the nozzle pressure and the hydraulic control valve opening, described by (see also [32])

where uk(t) and yk(t) now represent the hydraulic control valve opening and the nozzle pressure, respectively, andwk(t)results from the external disturbances and/or unmodeled uncertainties. Let the nozzle pressure control process be subject to nonrepetitive uncertainties arising from the initial shifts and the external disturbances in the form of

Fig. 1. Example 1: The input evolution versus iteration.

Fig. 2. Example 1: The convergence performance of the tracking error over the first 1000 iterations.

Fig. 3. Example 1: The tracking performance between the output learned after the 400th iteration and the desired reference.
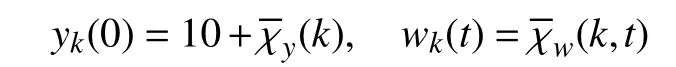

and our optimization-based adaptive ILC, which is comprised of the updating law (15) and the adaptive updating schemes S1) and S2), is applied by adopting the same parameters as shown in Table I and the same initial settings as used in Example 1. It can be validated that the needed robust convergence conditions of ILC in Theorems 1 and 2 are satisfied.
Similarly to Figs. 1–3, Figs. 4–6 are depicted to demonstrate the system performance of the injection molding process when operating with the use of our optimization-based adaptive ILC. The input evolution versus iteration is depicted in Fig. 4,which illustrates the boundedness of system trajectories. In Fig. 5, the robust convergence performance is illustrated for the optimization-based adaptive ILC by describing the evolution of the tracking error versus iteration. The highprecision tracking performance is demonstrated in Fig. 6 that describes the output learned with our optimization-based adaptive ILC after the 100th iteration, as well as the desired reference trajectory. It can be obviously seen that the illustrations of Figs. 4–6 coincide with our robust optimization-based adaptive ILC results of nonlinear systems.

Fig. 4. Example 2: The bounded evolution of the input versus iteration.
Discussions: The simulation tests performed in Examples 1 and 2 validate the robustness and effectiveness of our presented optimization-based adaptive ILC for nonlinear systems in spite of unknown nonlinearities and nonrepetitive uncertainties. Due to the limited use of model information,they also demonstrate that our optimization-based adaptive ILC results may provide a feasible way to the design and analysis of data-driven methods. In particular, the illustrations of Figs. 3 and 6 can disclose that our design method of optimization-based adaptive ILC works effectively for accomplishing the high-precision tracking tasks of nonlinear systems subject to the nonrepetitive uncertainties, especially in comparison with those methods proposed in, e.g., [16], [17].
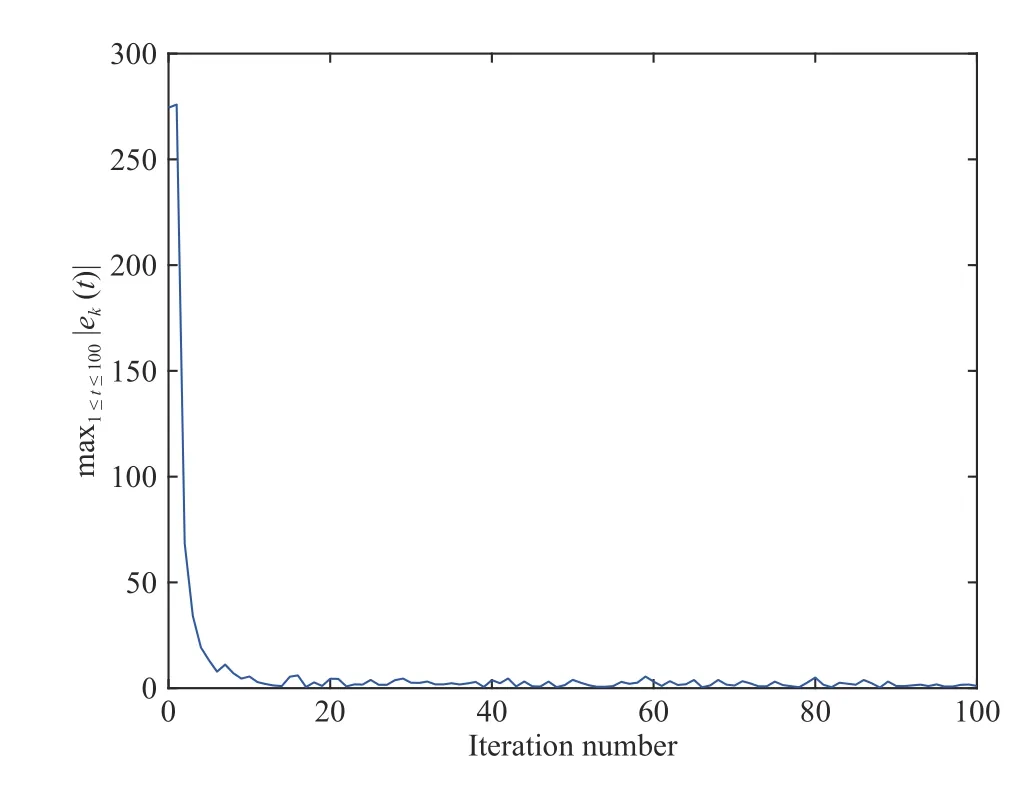
Fig. 5. Example 2: The robust convergence performance of the tracking error for the first 100 iterations.

Fig. 6. Example 2: The high-precision tracking performance between the output learned after the 100th iteration and the desired reference trajectory.
V. CONCLUSIONS
In this paper, robust convergence problems for the optimization-based adaptive ILC of nonlinear time-varying systems subject to iteration-dependent initial shifts and disturbances have been discussed. A new design method has been introduced to bridge the gap between optimization-based and CM-based approaches for ILC. By incorporating properties of substochastic matrices, a DDA approach integrated with CM-based analyses has been explored to establish robust convergence results of ILC, which avoids performing the eigenvalue analysis to gain convergence of iterative processes subject to iteration-dependent parameters.These advantages make our design and analysis methods for the optimization-based adaptive ILC effective and robust in spite of nonrepetitive uncertainties. In addition, the simulation tests implemented through a numerical example and for an injection molding process have demonstrated the validity of our robust optimization-based adaptive ILC results.


杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Review of Research and Development of Supernumerary Robotic Limbs
- Control of Non-Deterministic Systems With μ-Calculus Specifications Using Quotienting
- Decentralized Dynamic Event-Triggered Communication and Active Suspension Control of In-Wheel Motor Driven Electric Vehicles with Dynamic Damping
- ST-Trader: A Spatial-Temporal Deep Neural Network for Modeling Stock Market Movement
- Total Variation Constrained Non-Negative Matrix Factorization for Medical Image Registration
- Sampled-Data Asynchronous Fuzzy Output Feedback Control for Active Suspension Systems in Restricted Frequency Domain
