Sampled-Data Asynchronous Fuzzy Output Feedback Control for Active Suspension Systems in Restricted Frequency Domain
2021-04-13WenfengLiZhengchaoXieYucongCaoPakKinWongandJingZhao
Wenfeng Li, Zhengchao Xie, Yucong Cao, Pak Kin Wong, and Jing Zhao
Abstract—This paper proposes a novel sampled-data asynchronous fuzzy output feedback control approach for active suspension systems in restricted frequency domain. In order to better investigate uncertain suspension dynamics, the sampleddata Takagi-Sugeno (T-S) fuzzy half-car active suspension(HCAS) system is considered, which is further modelled as a continuous system with an input delay. Firstly, considering that the fuzzy system and the fuzzy controller cannot share the identical premises due to the existence of input delay, a reconstructed method is employed to synchronize the time scales of membership functions between the fuzzy controller and the fuzzy system. Secondly, since external disturbances often belong to a restricted frequency range, a finite frequency control criterion is presented for control synthesis to reduce conservatism.Thirdly, given a full information of state variables is hardly available in practical suspension systems, a two-stage method is proposed to calculate the static output feedback control gains.Moreover, an iterative algorithm is proposed to compute the optimum solution. Finally, numerical simulations verify the effectiveness of the proposed controllers.
I. INTRODUCTION
WITH the widespread application of vehicles, it is of great significance to improve the ride quality and driving safety of vehicles [1]–[8]. As an essential component of the vehicle chassis, suspension systems generally consist of three key components: linkages, spring elements and vibration absorbers, which play a critical role in the enhancement of ride comfort and handling stability [9]. In recent years, active suspension systems have been gaining an increasing research attention because of their excellent potentials to improve the three main performance requirements simultaneously, i.e., ride comfort, handling stability and road holding capability [10]. In the open literatures, much research effort has been devoted to the control synthesis of active suspension systems, such as disturbance-observer-based control [11], preview control [12],adaptive control [13], [14], fault tolerant control [15], eventtriggered control [16] and so on. To effectively address the uncertainties and nonlinearities encountered in active suspension systems and other engineering systems, Takagi-Sugeno (T-S) fuzzy-model-based control methods have drawn much attention owing to their capability of approximating any smooth nonlinear dynamic systems to any specified accuracy from the viewpoint of theory [15]–[23]. For instance, the authors in [15] presented a reliable fuzzy controller design method for active suspension systems with taking actuator delay and fault into account. A fuzzy control method was presented for uncertain vehicle suspension systems subject to the random incomplete communication links in [17]. The authors in [21] presented a fuzzy control approach for nonlinear electrohydraulic active suspension systems with consideration of input constraints. The authors in [19]presented a fuzzy dynamic sliding mode control method for active suspension systems. However, few of reported T-S fuzzy control methods were presented for the half-car active suspension (HCAS) model. To better investigate suspension dynamics, this work focuses on the T-S fuzzy control of HCAS systems.
With the rapid development of digital devices, most continuous-time systems are controlled via a high-speed digital computer, which are called as the sampled-data control systems [24]. Considering that the latest sampling signals are unchanged until the occurrence of next sampling, a lot of investigations have presented for the analysis and synthesis of sampled-data control systems, such as discrete-time system approach [25], [26], hybrid discrete/continuous-time approach[27] and input-delay approach [28], [29]. Among the above three main approaches, the input-delay approach has been widely adopted to analyze and synthesize the sampled-data control system, especially in the context of non-uniform sampling interval [24]. In this approach, an input delay is employed to represent the digital control law between two sampling instants. Based on the time-delay approach, a robust sampled-data H∞control method was presented for vehicle active suspension systems in [30]. The problem of fuzzy sampled-data control of the uncertain active suspension system was investigated in [29]. However, the premise variables of the fuzzy system and the fuzzy controller were assumed as identical in the above fuzzy control method. As pointed out in[20], [31], the fuzzy system and the fuzzy controller cannot share the same identical premise variables anymore due to the introduction of time delay. Hence, the asynchronous constraint needs careful treatments in the sampled-data control strategy, which is considered in this work.
It should be noted that the above sampled-data control methods are considered in the entire frequency range. In other words, the above methods ignore an important fact that external disturbances always belong to a certain frequency range. Under the finite frequency external disturbances, the above entire frequency control approaches are much conservative because of overdesign [32]. Moreover, according to ISO-2631, the vertical vibration between 4–8 Hz may cause a serious injury to human’s organs due to resonance.Regarding to finite frequency control, as a consequence,numerous fruitful results have been presented in recent years.As a milestone in the road of finite frequency control, the generalized Kalman-Yakubovich-Popov (KYP) lemma was developed in [33], [34], which is powerful to transform a frequency domain inequality into an equivalent linear matrix inequality (LMI). Based on the generalized KYP lemma, the authors in [35]–[39] carried out various studies on the robust state-feedback control of active suspension systems in restricted frequency range. However, a full knowledge of state variables is hardly available in practical suspension systems.To guarantee the feasibility of finite frequency control methods, the dynamic output feedback control strategy was investigated in [40]. Taking advantages of simple structure and convenient implementation, the finite frequency static output feedback control strategy was investigated in[41]–[45]. However, no above output feedback control method was focused on sampled-data T-S fuzzy HCAS systems with asynchronous constraints. That is still an open and challenging problem and motivates this work.
Motivated by above discussions, this paper proposes a sampled-data fuzzy static output feedback control approach for HCAS systems with asynchronous constraints in restricted frequency domain. The main contributions of this paper are as follows:
1) A reconstructed method is employed to synchronize the membership functions of the fuzzy controller and the fuzzy system, which is effective to address the asynchronous premise variables for sampled-data T-S fuzzy HCAS systems.
2) A new finite frequency controller design method is proposed for the concerned sampled-data asynchronous T-S fuzzy HCAS systems, which is effective to reduce conservatism under external disturbances over the concerned frequency range compared with the entire frequency controller presented in [29].
3) An iterative algorithm is proposed to compute the optimum fuzzy static output feedback controller for T-S fuzzy sampled-data HCAS systems in restricted frequency domain,which contributes significantly to maintain the feasibility of the controller.
The rest of this paper is organized as follows. Section II formulates the problem. The main results of control synthesis are given in Section III. Section IV verifies the performances of the proposed controllers via numerical simulations, and Section V concludes the research. Four useful lemmas,namely Lemmas 1 to 4, are presented in Appendix.
Notations: For a matrix P , PTand P−1denote its transpose and inverse, respectively. [P]sdenotes P + PT. * is used to represent a term that is induced by symmetry in symmetric block matrices or complex matrix expressions. A blockdiagonal matrix is denoted by diag{·}. Rndenotes the ndimensional Euclidean space. For matrices P and Q, the Kronecker product is denoted by P⊗Q.
II. PROBLEM FORMULATION AND PRELIMINARIES
A. T-S Fuzzy Model of Uncertain HCASs
For a better investigation into suspension dynamics, a typical uncertain HCAS model as shown in Fig. 1 is considered in this paper [20], [29]. The definitions of all symbols are listed in Table I. Assuming the pitch angle as a small one, the dynamic equations of the uncertain HCAS model can be obtained as follows:
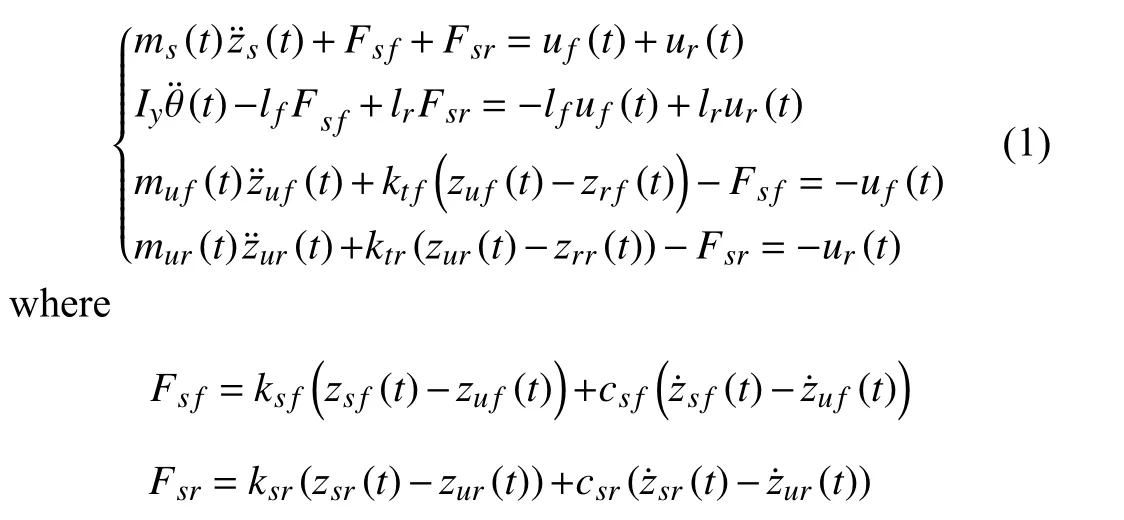
Fig. 1. Uncertain HCAS model.

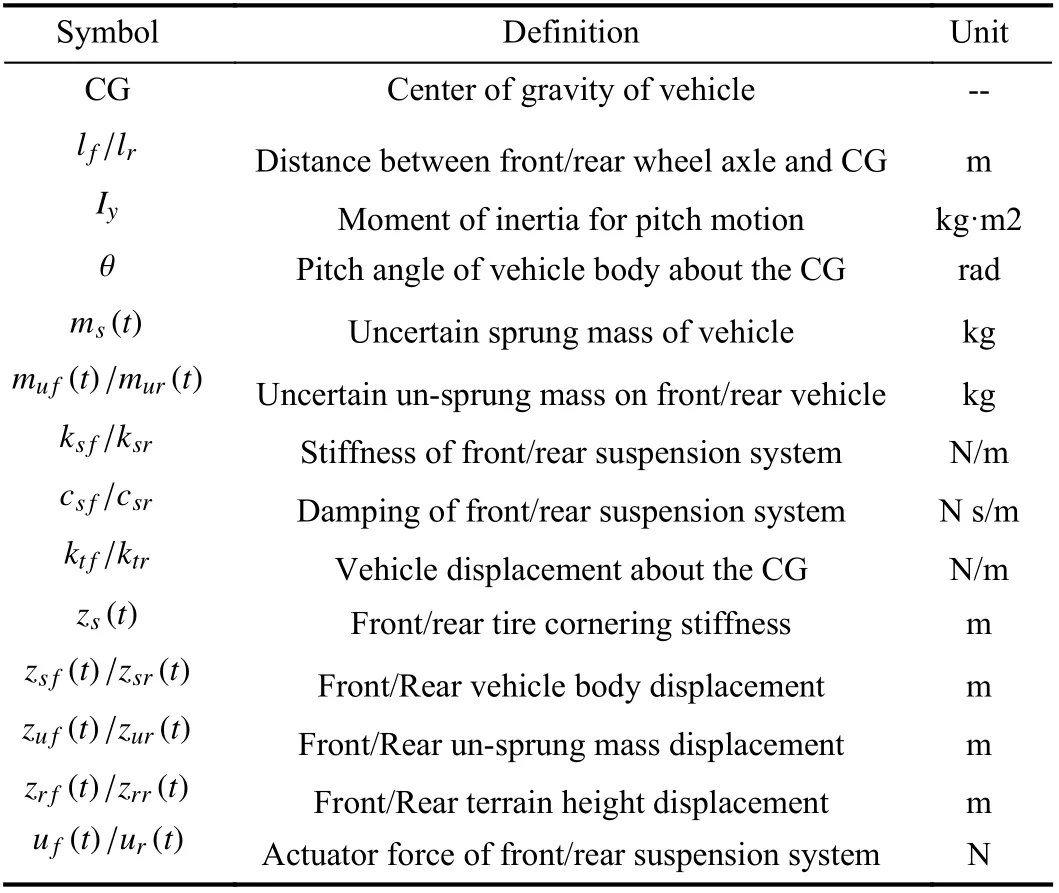
TABLE I SYMBOL DEFINITIONS OF HCAS MODEL


B. Sampled-data Fuzzy Output Feedback Control

C. Asynchronous Constraints and Problem Formulation
The overall structure of the sampled-data fuzzy control for HCAS systems is shown in Fig. 2. It is obvious that the premise variables of the fuzzy system and the fuzzy controller are unmatched. In other words, the asynchronous constraints of membership functions are of significance to be considered,which can be described as follows [16], [31]:

Fig. 2. Schematic diagram of sampled-data fuzzy control for HCAS systems.


III. MAIN RESULTS
In this section,a sampled-data fuzzy output feedback control algorithm is proposed for the T-S fuzzy HCAS system.
A. Problem Analysis


B. Parameterization of Controller


Similarly to the proof of Lemma 4, the inequalities (34) and(35) can be guaranteed by (29) and (30), respectively. Based on (27), (34) and (35), Theorem 2 can be obtained. ■
Remark 4: To deal with the problem of static output feedback controller design, a two-stage method was presented in [41], [42], [45]. However, the above literatures were focused on linear systems without consideration of time delay.Motivated by the two-stage method, Theorem 2 generalizes this idea to address the problem of sampled-data output feedback control in restricted frequency domain for T-S fuzzy HCAS systems with asynchronous constraints and transmission delay.
Remark 5: It should be noted that the inequalities in(29)–(31) are no longer LMIs because of the existence of KsTLj, where both Ksand Ljare unknown matrices.Nevertheless, if Ksis a priori known matrix, (29)–(31)become a set of LMIs, which are feasible to seek an optimal solution. Inspired by [42], [45], Kscan be fixed as a set of local control gains of a sampled-data fuzzy state feedback controller in finite frequency domain, i.e.Ksj=Ksjf,j=1,2,...,8(that is Stage 1). Therefore, the local sampled-data output feedback control gains can be obtained by solving Theorem 2 (that is Stage 2). As a special case, if defining Cy=I, a set of new local state feedback control gains can be obtained by solving Theorem 2, which is effective to update the initial state feedback control gains.
C. Computation of Controller
Note that a set of local state feedback control gains can be obtained by solving Lemma 4, hence, the following optimization problem is feasible to find a set of local output feedback control gains with an optimal performance index:
x111=0,x112=1;x121=0,x122=1;x131=1,x132=0;x211=1,x212=0;x221=1,x222=0;

Remark 6: Recalling Remark 5, if setting Cy=I, a set of updated state feedback gains can be obtained by solving (36).That contributes greatly to the iteration to search a set of local output feedback control gains with a smaller performance index. Based on above discussions, an iterative algorithm with implementation details is proposed to search a set of optimal local output feedback control gains, which is summarized in Algorithm 1.

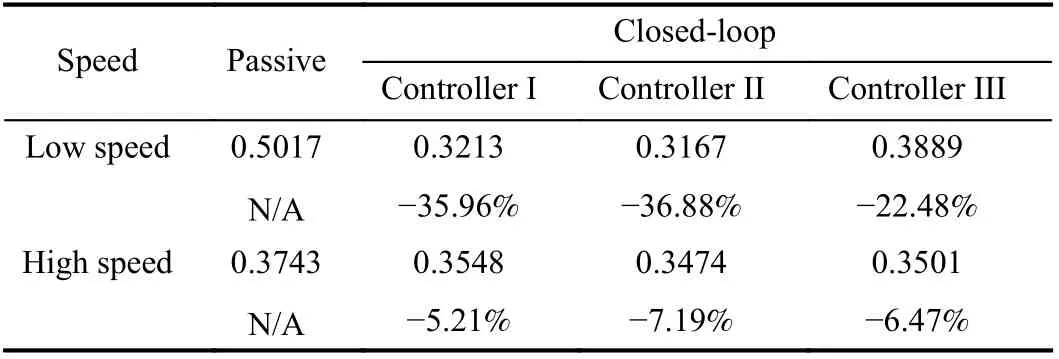
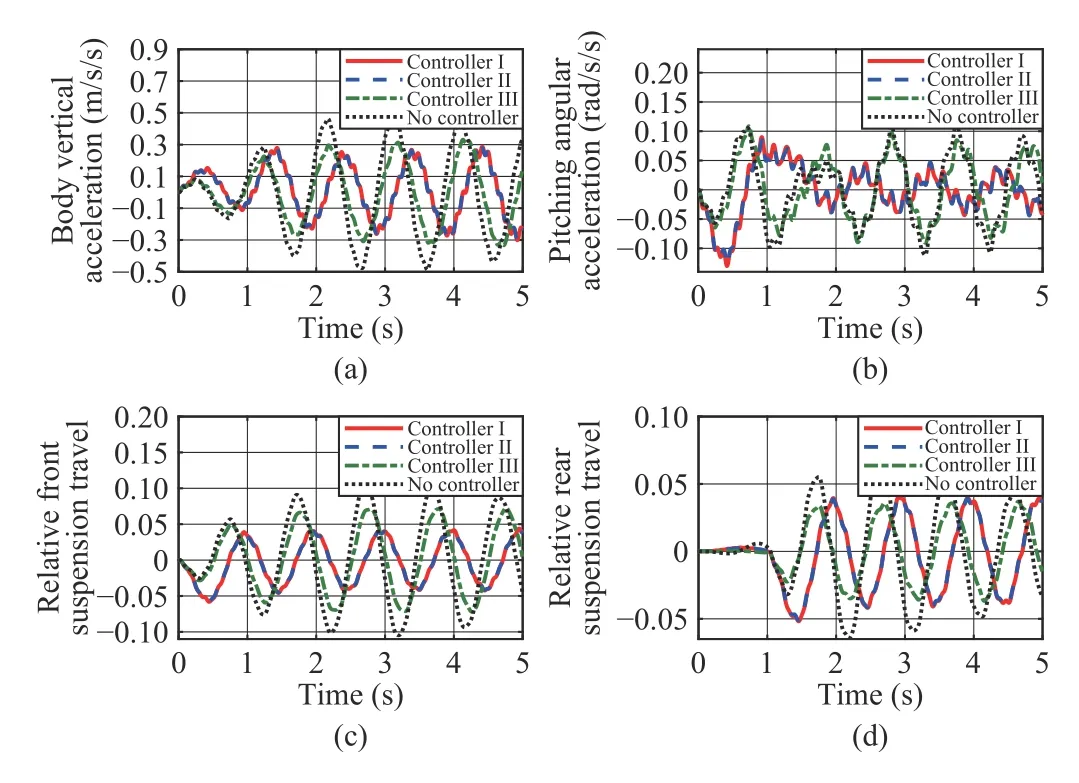
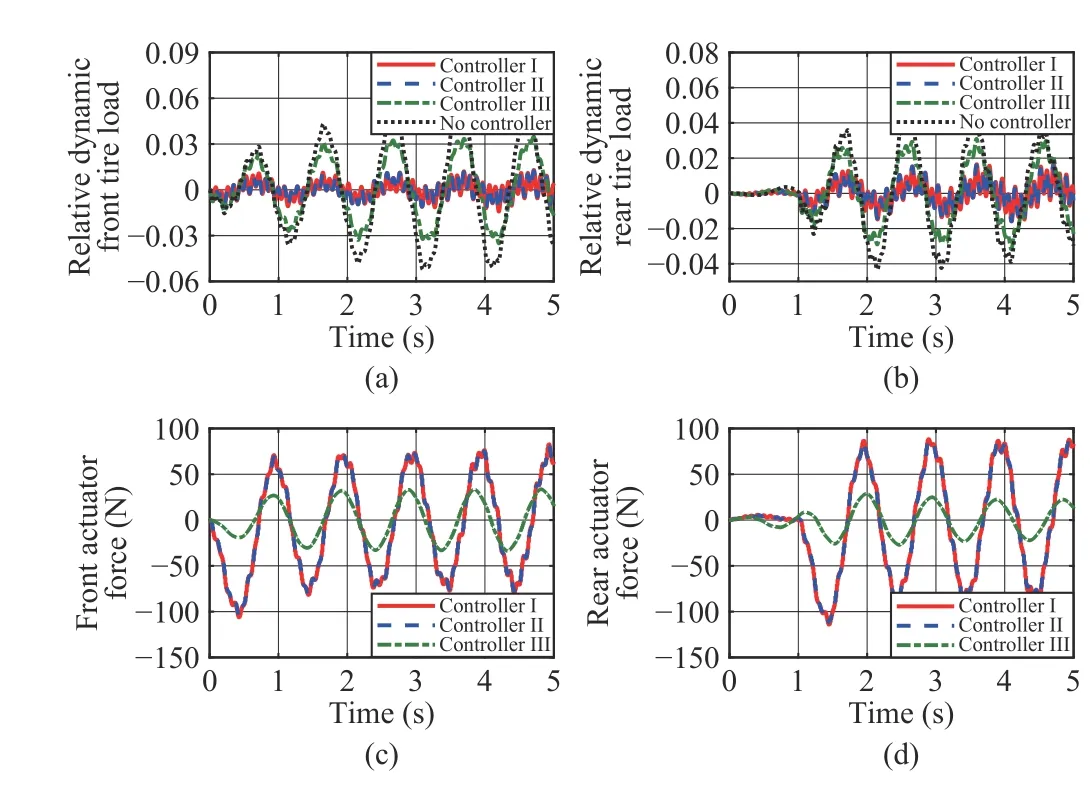
Algorithm 1 η∗ N∗Step 1: Input scalars T, ρ, λ1, λ2, α and , and choose the concerned frequency range.Step 2: Compute the initial local state feedback control gains via Lemma 4. Set i=1.Ksf(1)j Ksof(1)Step 3: Compute the initial local output feedback control gains and the corresponding performance index γ1 via the j Ks=Ksf(1)optimization in (36) with .Step 4:j i TABLE II PARAMETERS AND VALUES OF HALF-CAR SUSPENSION MODEL Fig. 3. Frequency response results for: (a) from z˙sf to z¨s, (b) from z˙sr to z¨s,(c) from z ˙sf to θ¨ and (d) from z ˙sf to θ¨. For description in brevity, the fuzzy output feedback controller is denoted as Controller II hereafter. To better highlight the effectiveness of the proposed controllers, another fuzzy sampled-data state feedback controller presented in [29]is adopted for comparative purpose, which is designed over the entire frequency range. The compared fuzzy sampled-data state feedback controller is denoted as Controller III and the control gains were presented in [29]. In this subsection, the results of frequency response are shown in Fig. 3. It should be noted that the uncertain parameters are fixed as ms=690 kg, muf=40 kg and mur=45 kgand the system is simplified as a continuous system. In all simulation results, the responses of the HCAS systems with Controllers I–III and no controller are denoted by red solid line, blue double-dashed line, green dash-dotted line and black dotted line, respectively. Fig. 3 shows that all the three controllers yield smaller gain values than that produced by the passive suspension system, which illustrates the effectiveness of the three controllers. It can also be observed from Fig. 3 that the gain values generated by Controllers I and II are smaller than that generated by Controller III, which indicates that the proposed Controllers I and II are more effective to improve ride comfort than Controller III. Moreover, Fig. 3 shows Controllers I and II have similar gain values, which illustrates the proposed Algorithm1 can derive a less conservative counterpart in static output feedback control. In a word, the frequency response results verify the performance of the proposed sampled-data fuzzy output feedback control algorithm. In this subsection, a typical bumped road profile is applied for simulation analyses, which is formulated as follows: Fig. 4. Bump response results at low speed for: (a) body vertical acceleration, (b) pitching angular acceleration, (c) relative front suspension travel and (d) relative rear suspension travel. Fig. 5. Bump response results at low speed for: (a) relative dynamic front tire load, (b) relative dynamic rear tire load, (c) front actuator force and (d)rear actuator force. Furthermore, Figs. 6 and 7 give the bump response results at high speed. Similarly to the case of low speed, it can be observed from Figs. 6 and 7 that all controllers yield a better ride quality than the passive suspension and guarantee the suspension hard constraints. Besides, Figs. 6 and 7 verify the advantages of the proposed controllers in comparison with Controller III. In addition, the root mean square (RMS) values of body vertical acceleration and pitching angular acceleration are listed in Tables III and IV. At low speed, the RMS values of body vertical acceleration and pitching angular acceleration can be reduced by 41.05% and 35.96% with Controller I,41.93% and 36.88% with Controller II and 37.42% and 22.48% with Controller III, respectively. At high speed, the RMS values of body vertical acceleration and pitching angular acceleration can be reduced by 30.89% and 5.21% with Controller I, 31.85% and 7.19% with Controller II and 21.45% and 6.47% with Controller III, respectively.Moreover, as shown in Tables III and IV, with the increase of velocity, a degradation of control performance is emerged,especially for pitching angular acceleration, which means the proposed controllers possess a limitation at high speed. Fig. 6. Bump response results at high speed for: (a) body vertical acceleration, (b) pitching angular acceleration, (c) relative front suspension travel and (d) relative rear suspension travel. Fig. 7. Bump response results at high speed for: (a) relative dynamic front tire load, (b) relative dynamic rear tire load, (c) front actuator force and (d)rear actuator force. TABLE III¨zs RMS VALUES OF UNDER BUMP ROAD DISTURBANCE TABLE IV RMS VALUES OF θ ¨ UNDER BUMP ROAD DISTURBANCE In a word, the bump response results verify the effectiveness of the proposed sampled-data fuzzy output feedback control algorithm. The following rough road is further considered to evaluate the performances of the proposed controllers, which is similar to the vehicle body resonance frequency with a highfrequency disturbance added to simulate the rough road surface [21], [46]: where zrr(t) is the same as zrf(t) but with a time delay of(lf+lr)/V and the velocity is chosen as V =10 km/h. Fig. 8. Rough response results for: (a) body vertical acceleration, (b)pitching angular acceleration, (c) relative front suspension travel and (d)relative rear suspension travel. Fig. 9. Rough response results for: (a) relative dynamic front tire load, (b)relative dynamic rear tire load, (c) front actuator force and (d) rear actuator force. The rough response results are plotted in Figs. 8 and 9. As shown in Fig. 8(a) and (b), the proposed controllers can reduce body vertical acceleration and pitching angular acceleration significantly compared with Controller III and the passive suspension. Figs. 8(c) and (d) shows both front and rear suspension travels lie in a feasible range. Figs. 9(a) and(b) reveals that the relative tire loads of both front and rear tires are less than one, which means an acceptable road holding property is achieved. Figs. 9(c) and (d) gives the front and rear actuator forces, respectively, which are less than the maximum actuator force. In a word, the rough response results verify the effectiveness and advantages of the proposed sampled-data fuzzy output feedback control algorithm. Remark 7: As for the implementation of the fuzzy controller, the estimation of sprung mass and un-sprung mass is necessary, which is a potential limit simultaneously. In practical vehicles, various estimation methods were presented for vehicle inertial parameters. For instance, the authors in[47] presented a dual unscented Kalman filter to estimate vehicle inertial parameters. The authors in [48] constructed an online state-parameter observer to estimate road irregularities and vehicle mass for suspension systems. Actually, the unsprung mass may be used as the nominal value to calculate weighting factors because the change in the un-sprung mass is small enough to be ignored [46]. This paper proposes a novel sampled-data fuzzy output feedback control algorithm for T-S fuzzy HCAS systems, in which the issues of asynchronous premises variables,uncertain sprung and un-sprung masses are considered. First,by the input delay approach, the sampled-data T-S fuzzy HCAS system is modeled as a continuous T-S fuzzy system with a time delay. Then the asynchronous premise variables are synchronized via a reconstructed method, which facilitates the controller design. Second, a two-stage method is applied to calculate finite frequency static output feedback control gains. Moreover, an iterative algorithm is proposed to search an optimum finite frequency output feedback controller.Numerical simulations on an uncertain HCAS model illustrate the advantages of the proposed fuzzy sampled-data output feedback control algorithm as compared with the previous entire frequency control method [29] and the passive suspension. The nonlinearities of components in suspension systems are ignored in this paper, which will be studied in the future work to improve the feasibility of the controller in real suspension systems. Moreover, the control performance at high speed should be further improved at the future work. APPENDIx Lemma 1 [49]: The sampled-data T-S fuzzy HCAS system in (20) is asymptotically stable for any time delayτ(t)satisfying 0 ≤τ(t)≤T, if there exist symmetric matrices P1>0, R1>0 and S1>0 such that the following inequality holds:IV. SIMULATION RESULTS






A. Frequency Response
B. Bump Response


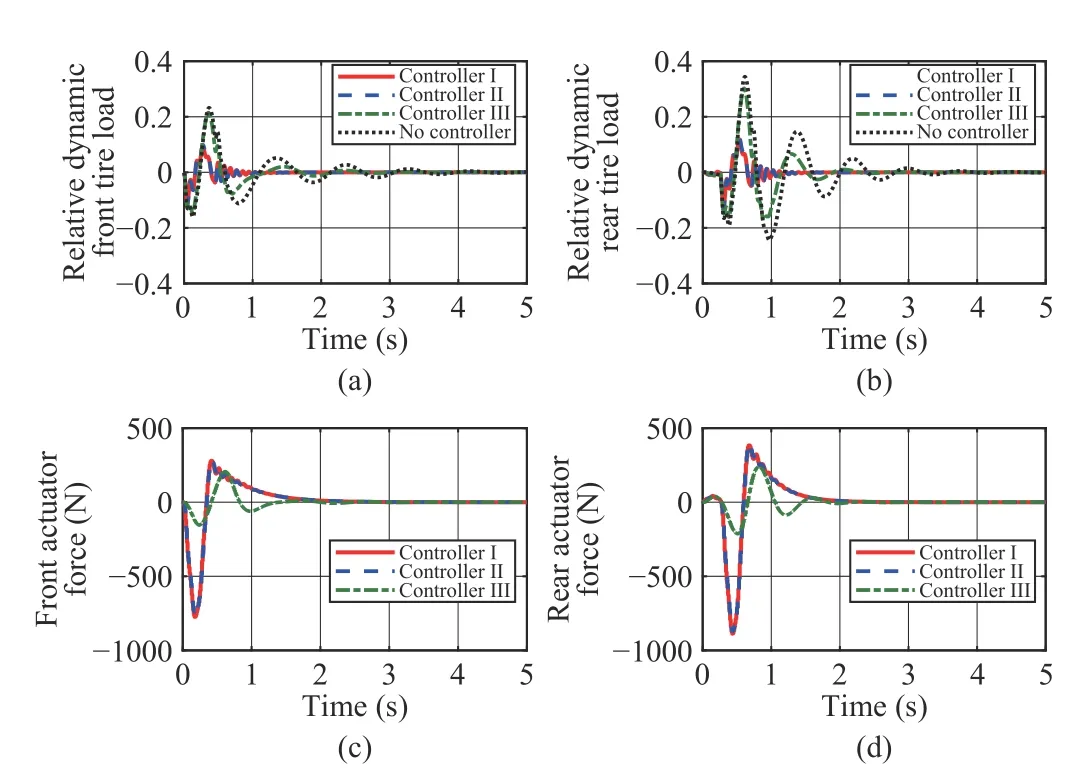



C. Rough Road Response

V. CONCLUSIONS




杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Review of Research and Development of Supernumerary Robotic Limbs
- Control of Non-Deterministic Systems With μ-Calculus Specifications Using Quotienting
- Decentralized Dynamic Event-Triggered Communication and Active Suspension Control of In-Wheel Motor Driven Electric Vehicles with Dynamic Damping
- ST-Trader: A Spatial-Temporal Deep Neural Network for Modeling Stock Market Movement
- Total Variation Constrained Non-Negative Matrix Factorization for Medical Image Registration
- Predicting Lung Cancers Using Epidemiological Data: A Generative-Discriminative Framework
