Total Variation Constrained Non-Negative Matrix Factorization for Medical Image Registration

Chengcai Leng, Hai Zhang, Guorong Cai, Zhen Chen, and Anup Basu, Senior Member, IEEE

Abstract—This paper presents a novel medical image registration algorithm named total variation constrained graphregularization for non-negative matrix factorization (TV-GNMF).The method utilizes non-negative matrix factorization by total variation constraint and graph regularization. The main contributions of our work are the following. First, total variation is incorporated into NMF to control the diffusion speed. The purpose is to denoise in smooth regions and preserve features or details of the data in edge regions by using a diffusion coefficient based on gradient information. Second, we add graph regularization into NMF to reveal intrinsic geometry and structure information of features to enhance the discrimination power. Third, the multiplicative update rules and proof of convergence of the TV-GNMF algorithm are given. Experiments conducted on datasets show that the proposed TV-GNMF method outperforms other state-of-the-art algorithms.

I. INTRODUCTION

IMAGE registration is an important research topic for aligning two or more images of the same scene taken at different times, viewpoints, or sensors [1]. Registration is widely used in computer vision and medical image processing, including multimodal image fusion, medical image reconstruction, and the monitoring of tumors. For example, the fusion of multimodal information can be realized by registering two images, which provides better visualization of anatomical structures and functional changes to facilitate diagnosis and treatment [2]. Area-based registration methods[3] mainly uses gray level information to optimize the maximum similarity measure, including mutual information(MI), by adapting optimization algorithms for registration [4].Gong et al. [5] proposed a novel image registration method including the pre-registration and a fine-tuning process based on scale-invariant feature transform (SIFT) and MI. Woo et al.[6] presented a novel registration method based on MI by incorporating geometric and spatial context to compute the MI cost function in large spatial variation regions for multimodal image registration. However, these methods are very sensitive to intensity variations and suffer from noise interference.Feature-based methods for image registration directly detect salient features and construct feature descriptors, which are robust and invariant to noise, illumination, and distortion.SIFT [7] is one of the most popular methods invariant to rotation, scale, translation, and illumination changes. Rister et al.[8] extended SIFT to arbitrary dimensions by adjusting the orientation assignment and gradient histogram of key points.

We can often treat the feature matching problem as a graph matching problem in image registration, since spectral graph theory [9] is widely used for image segmentation [10], [11],graph matching [12]–[15], and image registration [16]–[21].In order to make many algorithms practical in several real-life applications, dimensionality reduction is necessary. In order to avoid the curse of dimensionality, some dimensionality reduction matching or registration methods have been introduced [22]–[24]. Xu et al. [24] proposed such a method for high-dimensional data sets using the Cramer-Rao lower bounds to estimate the transformation parameters and achieve data set registration. In addition, some manifold learning methods [25] have also been presented, such as ISOMAP[26], locally linear embedding (LLE) [27], and Laplacian Eigenmap [28]. However, many of these algorithms have high computational complexity, and deal poorly with large data sets [29]. Liu et al. [30] proposed the text detection method based on morphological component analysis and Laplacian dictionary, which can reduce the adverse effects of complex backgrounds and improve the discrimination power of dictionaries.

Recently, some low-rank matrix factorization methods have been introduced in data representation [31]. Among these methods, non-negative matrix factorization (NMF) [32]achieves a part-based representation for non-negative data sets with applications in data clustering [33], [34] and data or image analysis [35], [36]. Some researchers, such as [37]−[40], also incorporated manifold learning information into NMF. Li et al.[39] proposed a graph regularized non-negative low-rank matrix factorization (NLMF) method by adding graph regularization into NLMF to exploit the manifold structure information and utilizing robust principal components analysis(PCA). Shang et al. [40] proposed a novel feature selection method by adding sparse regression and dual-graph regularization to NMF to improve the feature selection ability.Ghaffari and Fatemizadeh [41] presented a new image registration method by introducing correlation into the low rank matrix theory based on rank-regularized sum-of-squareddifferences (SSD) to improve the similarity measures. In addition, there are still very few NMF based methods used for image matching or image registration. Luo et al. have also published several papers [42]–[46] using non-negative latent factor models for high-dimensional and sparse matrices, which can be widely used in industrial applications and highly accurate web service QoS predictions. We will introduce a special sparse matrix factorization method for image registration called total variation constrained graphregularization for non-negative matrix factorization (TVGNMF).

Rudin et al. [47] first proposed the total variation (TV)method, which is effective for image denoising and can enhance the boundary features of large data sets. It can be used for various pattern recognition tasks, such as hyperspectral unmixing [48]–[50], data clustering [51], image restoration or image fusion [52]–[54], and face recognition[55], [56]. Thus, TV regularization is incorporated into NMF to enhance the details or features of the data. Graph regularization can also be added to NMF, which can discover the intrinsic geometric and structural information of the data.In the differential form of TV regularization, a diffusion coefficient is used to control the diffusion speed. This coefficient can denoise in smooth regions and preserve details in edges regions based on the gradient information. Therefore,our approach is a good part-based data representation that improves the data discrimination ability for clustering big data sets. We exploit this part-based data representation method to find better feature point matches for image registration.

In this paper, we propose a special part-based matrix factorization method, called TV-GNMF, which extends our previous work in [57]. The manifold graph regularization enhances and efficiently reveals the intrinsic geometric and structural information of the data, and the TV regularization denoises and preserves the sharp edges or boundaries to enhance the features of an image. We now explain why we incorporate TV regularization into TV-GNMF. In the TV regularization terms, the diffusion coefficient 1/|∇ H| is used to control the diffusion speed, which can denoise and enhance the edges or details based on the gradient information. If |∇ H|has a large value in the neighborhood of a point, this point is considered to be an edge and the diffusion speed is lowered to preserve the edges. Otherwise, if |∇ H| has a small value in the neighborhood of a point, and the diffusion is strong, it helps remove noise. We develop novel iterative update rules, prove the convergence of our optimization technique and give a matching algorithm based on TV-GNMF. Experimental results demonstrate the discrimination ability and better performance of our algorithm.

The remaining sections are organized as follows:Background work is introduced in Section II. Section III proposes the TV-GNMF method, detailed multiplicative update rules and proof of convergence of our optimization method. Section IV presents the image matching algorithm based on TV-GNMF. Experimental results are presented in Section V, before the conclusions in Section VI.

II. PRELIMINARIES

A. Symbols

First, we list some necessary symbols used in this paper in Table I.

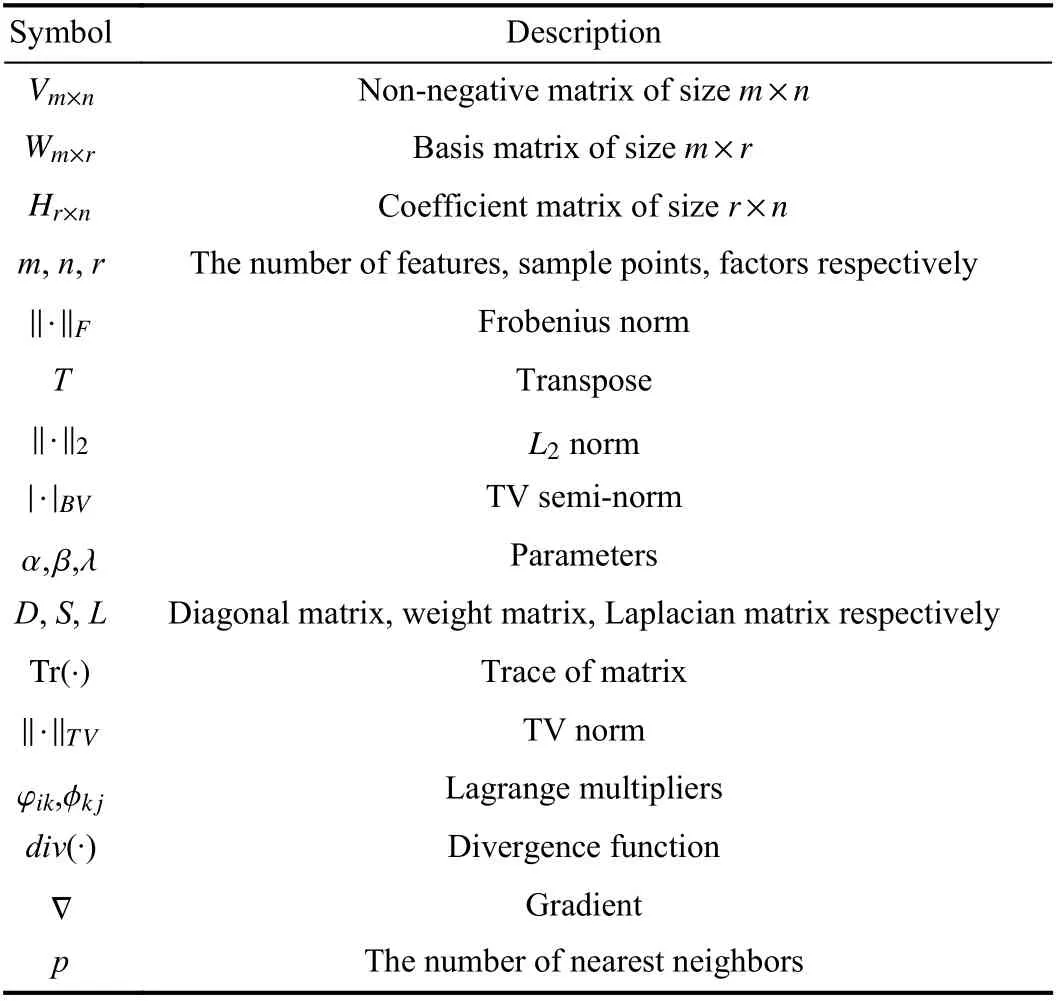
TABLE I SOME NECESSARY SYMBOLS

B. NMF

C. TV-NMF

Yin and Liu [56] proposed a new NMF model with bounded

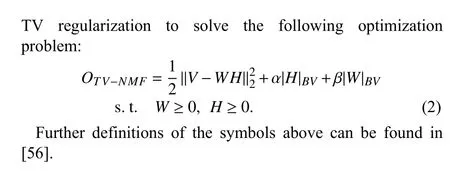
D. GNMF

Graph regularization is introduced into NMF, i.e., GNMF,to reveal the geometric information of the data [37], as follows:

III. TV-GNMF

In this section, we outline the idea behind the total variation method for enhancing or preserving edge features of data sets(images). The TV method is a form of anisotropic diffusion,which smoothens by selectively using diffusion coefficients based on the gradient information to retain image features while eliminating noise. Therefore, TV regularization and graph regularization are integrated with the NMF model to preserve edge features of the intrinsic geometry and structure information of the data. The proposed novel model called TVGNMF can enhance the intrinsic geometry and preserve edge characteristics of the data to improve discrimination ability for data clustering and image matching.

A. Total Variation

In order to enhance the edge features of the data, we introduce TV [47] regularization in this paper, defined as

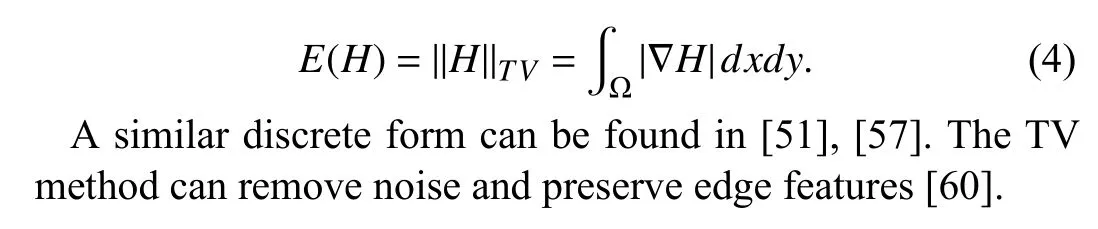
B. Multiplicative Update Rules

Based on TV regularization and graph regularization, the TV-GNMF model with TV regularization is given by

where λ, β ≥0 are parameters that can balance the

Algorithm 1 TV-GNMF Algorithm V ∈Rm×n S 1 ≤r ≤min{m,n}Input: , D, and .Initialization: , , , and .k=0,1...W0 H0λ β k=0 For until convergence or maximum iteration.Update according to Hk+1=Hk Hk+1(WT V+λHS+βdiv( ∇H ))k|∇H|(WT WH+λHD)k Wk+1 Update according to Wk+1=Wk (VHT)k(WHHT)k k=k+1 End W ∈Rm×r H ∈Rr×n Output: , .

We will describe a theorem related to the above iterative update rules along with the detailed proof of convergence.

TABLE II COMPUTATIONAL OPERATION COUNTS FOR EACH ITERATION FOR DIFFERENT METHODS

C. Proof of Convergence

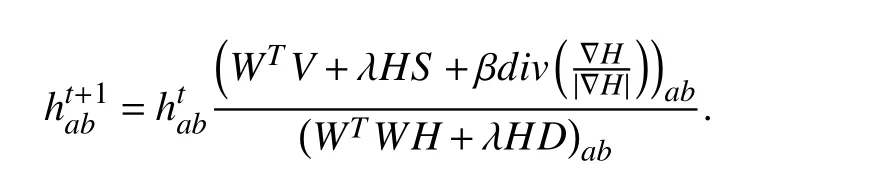
Theorem 1 guarantees convergence under the update rules based on (12) and (13). ■

D. Complexity Analysis

The computational complexity of the TV-GNMF method will be discussed and compared with the NMF and GNMF methods. Since Cai et al. gave the arithmetic operations of NMF and GNMF for each iteration in [37], we follow their results as shown in Table II. The main difference between TV-GNMF and GNMF is the component of TV norm.Specifically, to generate the divergence function of the discrete gradient matrix H, we need to calculate the first and second derivatives of each element, which results in 9 floating-point additions and 3 floating-point divisions.Moreover, the update rule of the divergence function of each element needs 3 floating-point additions, 7 floating-point multiplications, and one floating-point division. In general,compared to GNMF, our method adds 12 floating-point additions, 7 floating-point multiplications, and 4 floating-point divisions for each iteration. Note that m denotes the rows of an input image, whose scale is much larger than 12. Therefore,the overall complexity of our TV-GNMF is also O(mnr).Details of the complexity analysis are summarized in Table II.

In Table II, Fladd, Flmlt, Fldiv denote the number of floating-point additions, floating-point multiplications, and floating-point divisions, respectively; n represents the number of sample points; m is the number of features; and, r and p stand for the number of factors and the number of the nearest neighbors, respectively.

IV. IMAGE MATCHING ALGORITHM BASED ON TV-GNMF

To avoid confusion, the first part tests clustering performance of the data sets directly represented by the matrix V to compute matrices W and H based on (12) and (13),without using the following image registration algorithm. The data sets include images with many features or details and TV regularization can denoise and preserve details or edges of features to improve clustering performance.

The second part evaluates matching performance on medical images. We construct the non-negative matrix, not images, by exploiting geometric positions of feature points.TV regularization can enhance and characterize the intrinsic relationship of feature points based on diffusion depending on the gradient information of points. Further details on the matching algorithm of TV-GNMF can be found in [57].

V. ExPERIMENTAL RESULTS AND DISCUSSIONS

In this section, we provide some experimental evaluation of the proposed TV-GNMF method for image clustering and registration. There are two aspects in this study. We commence with an analysis of image data sets to demonstrate the clustering performance based on multiplicative update rules. The image matching performance is tested in the second part to show that the dimensionality reduction method has better discrimination ability for medical image registration.The clustering performance is evaluated in the first part.

A. Data Sets

The important statistics of the data sets used to evaluate the clustering performance are summarized in Table III. Further details can be found in [35], [37], [51].

TABLE III INFORMATION ON THE DATA SETS

B. Performance Evaluation and Comparisons

Performance is tested by comparing the labels obtained for each sample with the labels provided by the data sets. One metric is accuracy (AC), used to measure the percentage of correct labels obtained. The second metric is the normalized mutual information metric (NMI), used to measure how similar the two sets of clusters are. Detailed definitions of AC and NMI can be found in [33], [62].

In order to demonstrate our method’s performance on the above data sets, we compared TV-GNMF with two other related methods, i.e., the NMF [32] and GNMF [37] methods.The Frobenius norm is used to measure the similarity for the above three methods. We construct the weight matrix S of (3)and (5) using the 0-1 weighting based on the p-nearest neighbor graph, with p=5 for the GNMF and TV-GNMF methods. In addition, the regularization parameter λ is set to 100 for the GNMF method [37]; and the TV regularization parameter β is given and tested in the experiments for the TVGNMF method.

Table IV gives the data clustering results on the above four normalized datasets. In the experiments, the different cluster numbers are given on the Columbia University Image Library(COIL20) and Olivetti Research Laboratory (ORL) datasets for 100 iterations, and on the NIST Topic Detection and Tracking (TDT2) corpus dataset for 50 iterations. The regularization parameter β is set to 2 for the above three datasets in our TV-GNMF method. The number of iterations is set to 50 on the Pose, Illumination and Expression (PIE)face dataset for testing, and the parameter β is set to 0.2 in our TV-GNMF method. The GNMF method outperforms NMF,indicating that GNMF preserves or reveals the geometric structure of the data in learning under varying angles on the COIL20 dataset and different lighting and illumination conditions on the PIE dataset. Surprisingly, the average of AC and NMI of the GNMF method is lower than the NMF method for the ORL dataset. The GNMF method does not reveal the geometric information because the ORL database consists of 40 distinct subjects with varying lighting, different facial expressions, and details. Our TV-GNMF method has high accuracy and normalized mutual information. The TV-GNMF method improves clustering performance because it combines the merits of graphs and TV regularization to discover the geometric structure information and enhances feature details.The best results are highlighted in bold. In most cases, our TV-GNMF method has the best performance. However, in a few situations, GNMF has higher AC and NMI than ours for the underlined cases, such as when k=30 for PIE. Our method cannot preserve the sharp edges or boundaries to enhance the feature details because the PIE dataset consists of 68 distinct subjects with different lighting and illumination conditions. In addition, the parameter β also affects the clustering performance. Overall, our TV-GNMF method outperforms NMF and GNMF, and has better performance.Our TV-GNMF method preserves geometric structure information and enhances the edge features of the data as demonstrated in Table IV. Note that our method outperforms others in most cases, including every instance of the COIL20,ORL, and TDT2 datasets in Table IV. Even for the few situations where our method does not have the best score, we are within 2% of the top score. However, our model has two parameters, λ and β, which we need to choose adaptively or empirically.

In addition, we use the ORL dataset as an example to test the effectiveness of our method. We add Gaussian noise with mean 0, and variance 0.09, based on the NMF, TV-NMF,GNMF, and TV-GNMF methods under the same conditions,with parameter β=2, and 50 iterations, for different cluster numbers. We can see that TV-GNMF has the best clustering results as shown in Table V. This happens because TV regularization can remove noise and preserve the details or features of the data, and graph regularization can discover the intrinsic geometric and structural information of the data while removing noise and enhancing features. TV-NMF has better results than NMF and GNMF, because GNMF cannot discover or reveal the intrinsic geometric and structural information of the data well in the presence of noise.

C. Parameter Evaluation

In this section, stability is tested based on our TV-GNMF method for various parameter settings. Our model has two important regularization parameters: λ and β. The GNMF method produces the best results when λ is set to 100. In our model, λ is also set to 100, and we vary the regularization parameter β to test stability. The performance of TV-GNMF varies with the β on COIL20 and PIE datasets as shown in Fig.1, which shows that TV-GNMF is very stable with respect to β. Fig. 1(a)−1(c) give the clustering performance when the regularization parameter β varies from 0.1 to 20 for different classes; such as 8, 13, and 18 on the COIL20 dataset. Fig. 1(d)−1(f) also present the clustering performance when the parameter β varies from 0.1 to 35 under different classes,such as 20, 35, and 50 on the PIE dataset. For a big range of the regularization parameter on the two data sets, TV-GNMFhas consistently good and stable performance. For the COIL20 dataset, our method produces relatively big clustering results based on parameter evaluation when β=5. The reason is that the randomness of the initial values of W and H affect the clustering performance. The initial values are randomly generated by non-negative constraints when we execute TVGNMF with β varying from 0.1 to 20 for different numbers of clusters, which can only ensure convergence to a local optima as they are updated iteratively. However, from the second experimental results, the range of the regularization parameter is larger than the first and has higher accuracy.

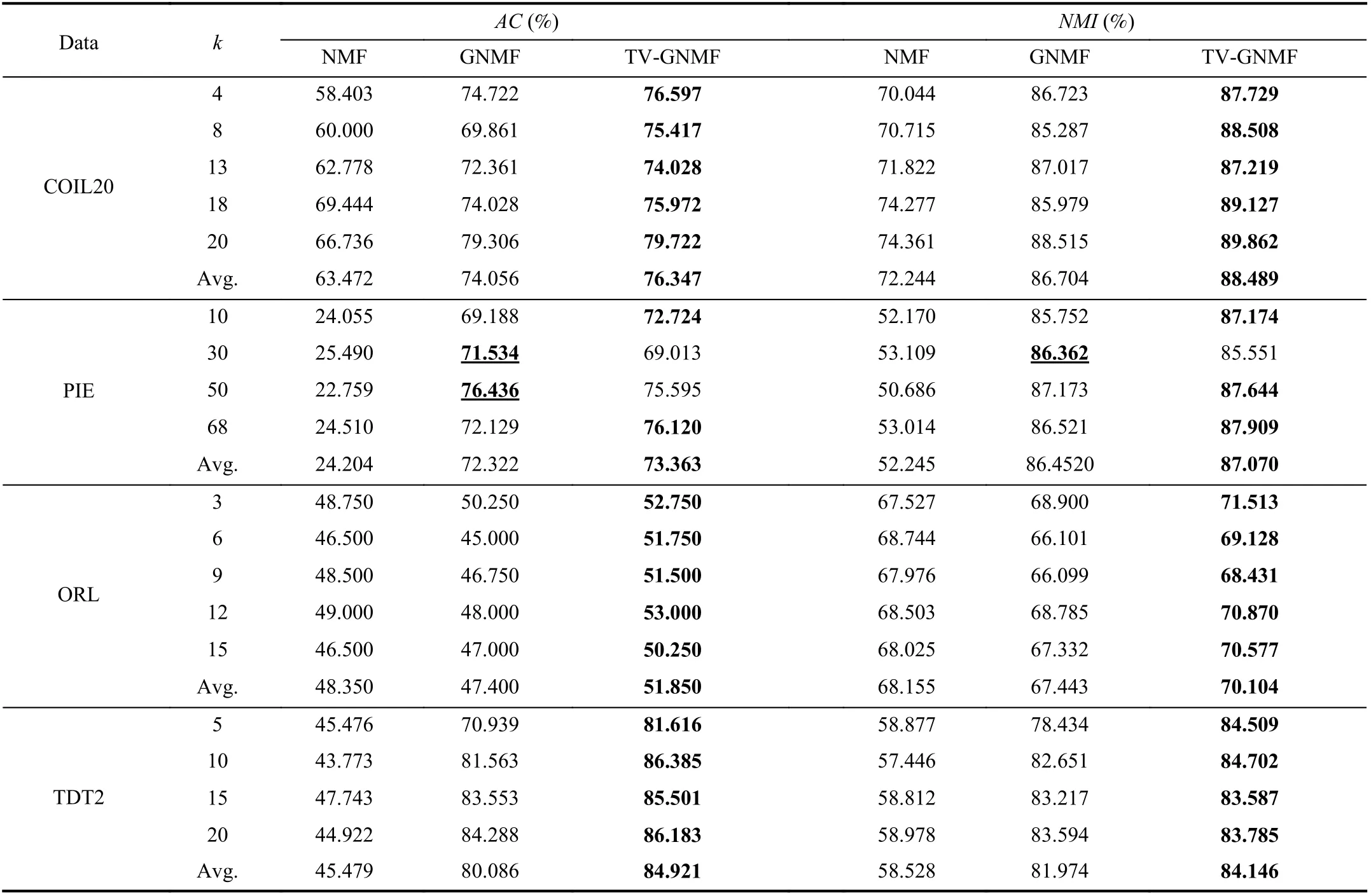
TABLE IV COMPARISONS ON COIL20, PIE, ORL AND TDT2 DATASETS

TABLE V COMPARISONS ON ORL DATASET WITH NOISE

In addition, we also use the ORL dataset as an example to test the effectiveness of our method with different p based on the GNMF and TV-GNMF methods under the same conditions with λ=100 and 50 iterations, cluster number set to 16 classes and β set to 2 in the TV-GNMF method. As we have seen, GNMF and TV-GNMF use a p-nearest neighbor graph to capture the local geometric structure information on a scatter of data points. GNMF and TV-GNMF have better clustering performance based on the assumption that two neighboring data points share the same label. When there are more nearest neighbors p, this assumption is more likely to fail. This is the reason why the performance of GNMF and TV-GNMF declines, and TV-GNMF is still superior to GNMF as p increases, as shown in Table VI and in Fig. 2.

D. Medical Image Registration Performance

Fig. 1. Performance of TV-GNMF for varying regularization parameter β on COIL20 and PIE datasets.

Fig. 2. The performance of GNMF and TV-GNMF decreases as p increases on ORL dataset.

TABLE VI COMPARISONS ON ORL DATASET WITH THE DIFFERENT p

In this section, a novel low-rank preserving technique is proposed by matching feature points to verify the discrimination ability to achieve one-to-one correspondences.We must emphasize that feature point detection or feature point description is not our research focus. The key issue is how our TV-GNMF method exhibits discriminating power to capture the intrinsic geometry and structure information and finds one-to-one correspondences between feature points. In order to test the matching performance, we applied it to medical images demonstrating that the proposed method has the discriminating power to achieve stable one-to-one feature correspondences. Furthermore, we compare the results of our TV-GNMF method with the projection clustering matching method (Caelli’s method) [23] and Zass’ method [63] in terms of matching.

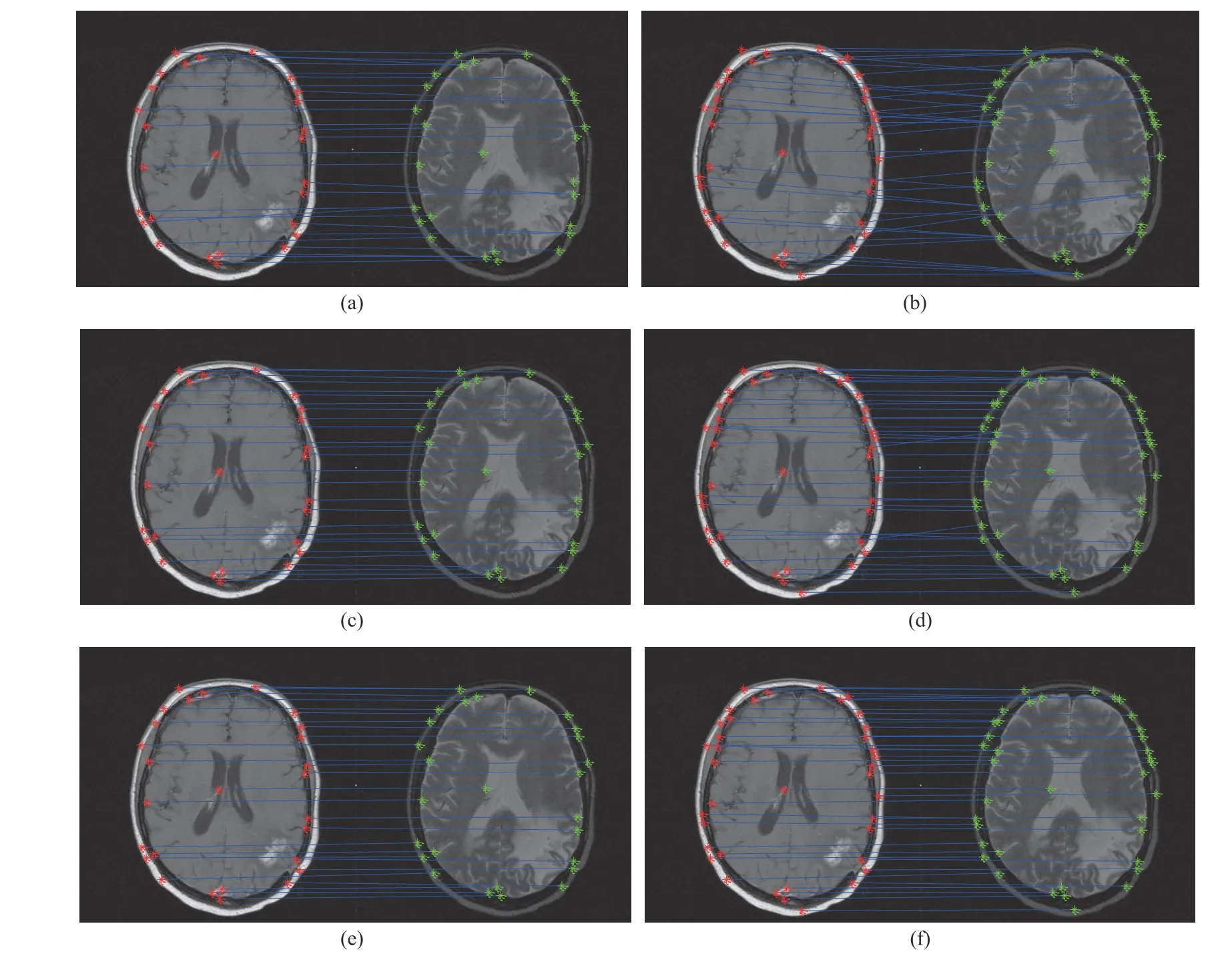
Fig. 3. Matching results: (a) and (b) Caelli’s method; (c) and (d) Zass’ method; (e) and (f) Our TV-GNMF method.

The 32nd slice of T1 and T2 of a magnetic resonance imaging (MRI) sequence is used to test, and the image matching results are given in Fig. 3. T1 denotes prominent tissue T1 relaxation (longitudinal relaxation) difference,which is used to observe anatomical structures. T2 denotes prominent tissue T2 relaxation (transverse relaxation)difference, which is used to show tissue lesions. We use the Harris Corner Detector [64] to extract 27 feature points and 38 feature points from Figs. 3(a), 3(c), and 3(e), and Figs. 3(b),3(d), and 3(f), respectively. Obviously, Fig. 3(a) produces some two-to-one mismatches. Zass’ and our methods achieve one-to-one correspondences in Figs. 3(c) and 3(e),respectively. In addition, some feature points are added as shown in Figs. 3(b), 3(d), and 3(f). More many-to-one correspondences are produced by Caelli’s method in Fig. 3(b)when the number of feature points is increased. The reason is that if the distances between some of the extracted points are very close to each other, they are more likely to be in the same class. Thus, more many-to-one correspondences are produced.Zass’ method is better than Caelli’s method because the matching problem utilizes a probabilistic framework based on hypergraphs. However, this method also produces some mismatches as shown in Fig. 3(d). Despite some feature points being very close to each other, our method can still find oneto-one correspondences, as seen in Fig. 3(f). This result indicates that our method has better discrimination ability to improve matching performance, thereby achieving robust image registration. We also utilize the computation time to evaluate the quantitative analysis, and the computation time for the entire matching process, including feature point extraction, in Table VII. This table indicates that our method needs less computation time. Please see [57] for additional details.

In addition, we also use our method to test the matching ability compared to a more classical and effective method called the coherent point drift (CPD) method [65]. We use the Harris Corner Detector to extract 156 feature points in T1 (red “*”) and T2 (blue “o”) of the 24th slice of an MRIsequence. The test experiment is intended to show the effectiveness of our method. We execute the CPD algorithm and our matching algorithm on the feature point sets. Both methods have good matching performance based on the experimental matching results shown in Fig. 4. However, our method takes 0.481 s less than the 0.990 s needed by the CPD method. This indicates that we have introduced an effective matching method that is also computationally more efficient.

TABLE VII COMPARISON OF THE COMPUTATION TIME (s)AS SHOwN IN FIG. 3

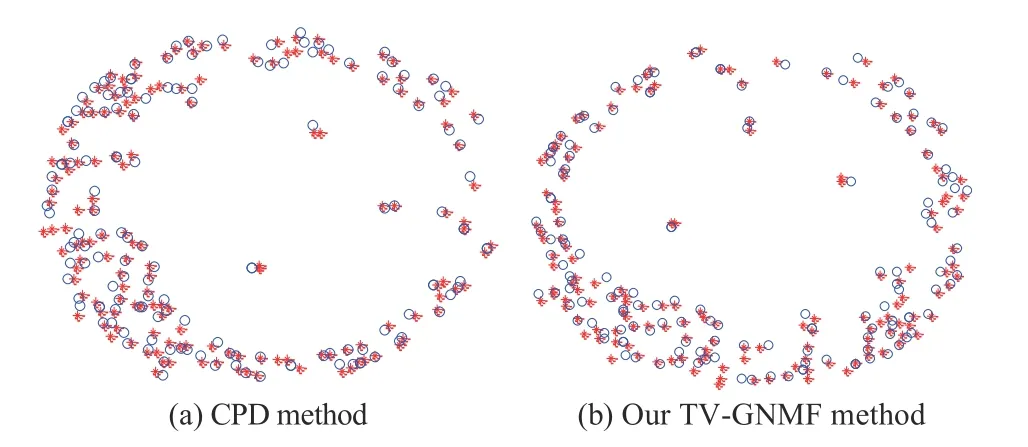
Fig. 4. Matching results for a feature point set.

To test the accuracy of registration, the root mean squareerror (RMSE) is used to evaluate the accuracy. Detailed results can be found in [57].

TABLE VIII COMPARISON OF COMPUTATION TIME AND ACCURACY FOR DIFFERENT IMAGE MODALITIES

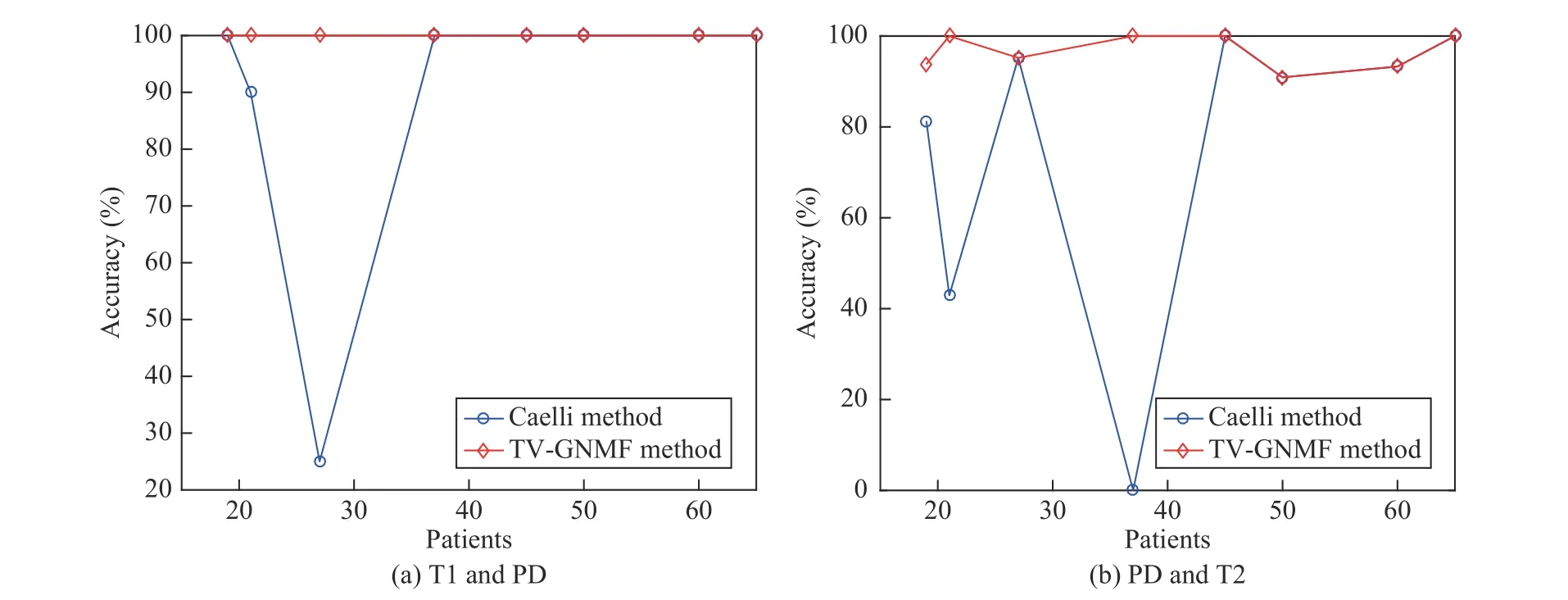
Fig. 5. Plot of accuracy considering different slices for the different patients of Table VIII.

Finally, to verify the discrimination ability and robustness under different medical image modalities, we give the accuracy which is defined as Nc/N, where Ncdenotes the number of correct matches and N denotes the total number of feature points. Table VIII summarizes eight experiments including different patients, with each patient repeated twice.It also shows the computation time and accuracy for different patients from the brain datasets [66], and is compared with Caelli’s method. These experiments show that the proposed method has better discrimination ability in finding one-to-one correspondences and has good matching results. The reason for large fluctuation in accuracy in Caelli’s method for different patients is that if the distances between feature points are extracted very close to each other, it is more likely that these points are in the same class. This produces many-to-one correspondences to create a large fluctuation in accuracy. Fig. 5 shows the matching performance for different patients in Table VIII. For this figure, the y-axis represents the accuracy and the x-axis denotes the patients. The different numbers of feature points are obtained by using the Harris Corner Detector under the same condition for different patients, and the number of feature points detected is relatively small.Therefore, the computation time is less than 1.0 s and the time difference is not big. However, the results (in bold) are not as good for some patients based on Caelli’s method, as shown in Table VIII and Fig. 5. Thus, the experimental results indicate that our method is robust and has more discrimination ability than Caelli’s.

Fig. 6. Discrimination and robustness considering the same patient for different number of feature points. (a) Feature point extraction results of reference and sensed images; (b)−(d) Caelli’s method; (e)−(g) TV-NMF method; (h)−(j) GNMF method; (k)−(m) TV-GNMF method.

Fig. 6 also shows the discrimination ability and robustness on the 65th patient of PD and T2 by increasing the number of feature points. PD reflects the difference in hydrogen proton content for different tissues, i.e., comparison of hydrogen proton density in prominent tissues. Fig. 6 compares the matching results based on Caelli’s method, TV-NMF method,GNMF method, and our method. We can see that the matching results, whether correct or incorrect, more clearly,when there are relatively few feature points and matching lines. For example, for Figs. 6(d), 6(g), 6(j), and 6(m), the matching results have many matching lines used to connect the reference and sensed images. This makes it difficult to see the texture of images due to many mismatches, as shown in Fig. 6(d). In order to avoid this problem, we show decomposition results with the feature points of the reference image (left) and the sensed image (right); which are first extracted as shown in Fig. 6(a). Then, these points are used for image matching as shown in Figs. 6(d), 6(g), 6(j), and 6(m).For these experimental results considering more feature points, our method still has better matching results, as shown in Fig. 6(m), than the TV-NMF method (Fig. 6(g)) and the GNMF method (Fig. 6(j)). However, Caelli’s method has completely different results, as shown in Fig. 6(b)−6(d), for different number of feature points. This indicates that our method has good discrimination ability and robustness, and achieves one-to-one correspondences regardless of the number of feature points.

E. Summary

Based on the theory and empirical studies, we summarize that:

1) The proposed TV-GNMF model is able to accurately achieve data clustering and image registration in a low dimensional feature space. Hence, TV-GNMF outperforms other state-of-the-art algorithms in accuracy of clustering,registration, and time efficiency.

2) Total variation constraint and graph regularization can control the diffusion speed to denoise and preserve the features or details of the data. This is achieved by a diffusion coefficient based on the gradient information to reveal intrinsic geometric and structural information of features to enhance the discriminating power.

3) Iterative update rules are developed and a proof of convergence for the TV-GNMF algorithm is given.

VI. CONCLUSIONS

In this paper, we proposed a novel matrix factorization method called TV-GNMF, which can effectively remove noise and preserve the data features utilizing total variation.Our method can also reveal the intrinsic geometric and structural information of the data well to improve discrimination ability. Experimental results on data sets and images indicate that TV-GNMF is a better low-rank representation method for data clustering and image registration. There are two parameters, λ and β, that play a key role in our model. How to adaptively choose the values of λ and β will be investigated in our future work.

ACKNOwLEDGMENT

The authors would like to thank Prof. D. Cai, in the College of Computer Science at Zhejiang University, China, for providing his code for implementing GNMF.