基于飞行实测的直升机操纵与载荷特性

2021-04-13李永寿

科学技术与工程 2021年7期

李永寿

(中国飞行试验研究院，西安 710089)

直升机稳态飞行时的操纵和载荷特性研究的主要目是获取直升机4个操纵量、2个姿态角和结构载荷随前飞速度等的变化规律。这是分析研究直升机飞行力学、结构动力学、操纵品质以及振动、噪声、疲劳载荷学科的重要基础，其正确与否不仅影响对直升机飞行操纵品质的分析，也会影响对直升机振动载荷的分析。

常规的综合气弹分析方法[1-2]预估直升机的操纵与载荷特性，普遍采用升力线理论或查表法等气动模型，很难捕捉细致的流场特性，无法满足直升机稳态飞行时操纵量与振动载荷的计算精度要求[3-4]。近些年，随着计算流体力学(computational fluid dynamics，CFD)技术的发展，国外学者首先将CFD 气动模型引入传统气动弹性模型，目的是将CFD 计算的气动载荷传递给结构模块，而结构模块又将计算的结果反馈给CFD模块，这就诞生了一种基于“CFD/CSD”耦合的计算方法，该方法克服了传统综合气弹分析方法中气动模型精度不足的缺陷，提升了对直升机的操纵和载荷特性的预估精度。比如2015年，Lim[5]耦合了基于Navier-Stokes方程的OVERFLOW2和CAMARADⅡ软件，考虑多段桨尖影响，对旋翼载荷特性和气动特性尝试了优化设计并取得了初步结果。目前，中国都是通过利用国外的样例直升机动力学模型和飞行试验数据开展CFD/CSD耦合方法研究，但起步较晚，仍处于发展阶段。其中南京航空航天大学研究得比较多，比如王松[6]、余智豪等[7]、马砾等[8]、黄道博[9]、李建东[10]、王俊毅等[11]、吴少杰等[12]、吴杰等[13]在近年来先后开展了CFD/CSD耦合方法在直升机桨叶振动载荷、配平预估上的应用研究，取得了一定成果。尽管CFD/CSD耦合方法相比传统的综合气弹分析方法，在气动模型上更加保真，能够保证一定的计算精度，但与真实飞行试验结果对比后仍然存在不小差距，比如在振动载荷的高频成分与相位预估上误差较大、在低速段的配平操纵量预估上不尽理想、桨叶模型和气动模型等对预估结果的影响较大，同时对尾桨、垂尾、旋翼轴等关键结构载荷鲜有涉及等诸多问题。

综上可见，无论是综合气弹分析方法还是CFD/CSD耦合方法，都需在直升机操纵与载荷特性的预估精度上不断改进和完善，方能投入到真正工程应用上。而要实现这一目标的最有效的技术途径就是利用大量的飞行试验实测结果来进行模型与方法的修正与完善，进而达到预测结果与飞行实测结果的尽可能吻合，从而提升预估精度。但是由于中国在这方面研究工作起步较晚，一直以来尚未在直升机型号上专门开展此类的飞行试验工作。为此，现从直升机飞行试验角度出发，利用某型直升机开展直升机操纵与载荷特性的飞行实测方法研究，并给出最终实测结果，供相关研究机构和人员借鉴与参考。

1 试验准备

1.1 飞行状态参数确定

直升机稳态配平飞行时的操纵特性，是研究直升机操纵量和姿态角随前飞速度的变化规律。此时作用在直升机上的全部外力、外力矩合成为零，即处于平衡状态，其平衡方程是总距、横向周期变距、纵向周期变距、尾桨距、俯仰角和侧倾角的非线性方程组，可表示为

f(φ7,A1,B1,φT,θ,γ)=0

(1)

式(1)中：φ7为总距；A1为横向周期变距；B1为纵向周期变距；φT为尾桨距；θ、γ分别为直升机的俯仰角和侧倾角。

为此，飞行试验中需测量上述6个参数。除此之外，还需测量包括直升机的飞行高度、速度、发动机扭矩、航向角、总距操纵位移、横向操纵位移、纵向操纵位移、脚蹬操纵位移等参数以识别直升机不同飞行状态，如表1所示。其中，序号1～10的测试参数通过抽引直升机自带的测试信号数据获得；序号11～14的测试参数通过加装线位移传感器获得，飞行状态参数采样率一般情况取为16 Hz。

表1 飞行状态参数Table 1 The flight state parameters

1.2 载荷参数确定

直升机在稳态配平飞行时，由于受外界真实大气环境及操纵等影响，旋翼、尾桨和传动系统等旋转部件，在运转时会产生持续的周期性的交变载荷。其中旋翼、尾桨桨叶主要承受挥舞弯矩、摆振弯矩、扭矩；旋翼轴承受扭矩、弯矩、轴向力；变距拉杆承受轴向力，垂尾承受弯矩。图1～图5为旋翼桨叶、尾桨叶、变距拉杆、旋翼轴、垂尾等部件的测载剖面。

图1 桨叶测载剖面Fig.1 Load measurement section of rotor blade

图2 尾桨叶测载剖面Fig.2 Load measurement section of tail rotor blade

图3 变距拉杆测载剖面Fig.3 Load measurement section of pitch link

图4 旋翼轴测载剖面Fig.4 Load measurement section of rotor shaft

图5 垂尾测载剖面Fig.5 Load measurement section of vertical tail

上述载荷在飞行试验中是利用惠斯登电桥并通过电阻应变计予以测量。其测量原理是应变计将测点应变转换成应变计电阻的变化，并以电桥的输出电压表征出来，最后通过将输出电压与标定试验获得的载荷方程联立就能得到交变载荷。

为了确保飞行实测中对高频成分载荷的捕获，采样率一般不应低于最高阶载荷分析频率的8～12倍，并圆整归类到2n(n为正整数)。表2列出了载荷测量部件名称、载荷属性、组桥方式以及采样率。

表2 载荷测量的部件、组桥方式和采样率Table 2 Components,bridge combination and sampling rate of load measurement

图6为测量弯矩、轴向力和扭矩的惠斯登全桥电桥的组桥连线示意图。

BENDING为弯矩；TENSION为轴向力；TORSION为扭矩；P-、S-、P+、S+分别为惠斯登电桥的激励电压负极、输出电压负极、激励电压正极、输出电压正极图6 全桥连线示意图Fig.6 Schematic diagram of full bridge connection

1.3 试验流程

飞行实测前，需完成传感器标定、传感器和测试设备加改装、地面通电联试和测试检飞等一系列试验过程。待测试设备工作正常，试验数据正确有效后，方可开始飞行实测。图7为飞行试验流程图。

图7 飞行试验流程图Fig.7 Flow chart of flight test

首先，根据测试参数制订测试任务书，包括测试目的、测试原理、测试设备、测试状态、测试科目、测试程序、测试条件和测试要求等内容；其次，对传感器标定及加装；再次，将飞行状态测试参数和静部件载荷参数接入机载测试系统；旋翼载荷参数接入旋翼载荷测试设备与旋翼同步旋转，尾桨载荷参数接入尾桨载荷测试设备同尾桨一同旋转；上述3个测试设备均要求时间同步；最后，对测试参数记录、处理与分析，得到直升机操纵与载荷特性。

图8为测试设备的机上的位置示意图。

图8 测试设备机上位置示意图Fig.8 Schematic diagram of test equipment position on the helicopter

1.4 试飞方法

采用稳定悬停及稳定平飞法开展飞行试验，选取直升机在正常起飞重量、正常重心条件下，开展了稳定悬停及不同速度稳定直线平飞科目的飞行试验。

2 操纵量和姿态角实测结果及分析

2.1 俯仰角随前飞速度变化关系

为了便于对飞行实测操纵量及姿态角的理论分析，图9为直升机在稳态前飞时的力和姿态的关系[14]。本文所给的操纵量和实测结果均作了归一处理。

TPP为旋翼桨尖平面；S-S为旋翼桨毂平面；T为旋翼拉力；H为旋翼后向力，Fx,F为机身气动力在体轴系下x轴的分量，也称为机身阻力；Fy,H为平尾产生的垂向力在体轴系下y轴的分量；Mz,F为机体俯仰力矩在体轴系下z轴的分量；G为直升机重力；α1s为旋翼挥舞后倒角；α1s为旋翼迎角；δ为旋翼轴前倾角图9 直升机前飞时力及姿态的关系Fig.9 Realtionship between force and attitude of helicopter in forword flight

将图9各力投影到桨毂平面，略去小量，可求得旋翼迎角的表达式为

(2)

将式(2)与俯仰角和旋翼迎角的关系联立得到俯仰角的表达式为

(3)

由式(2)、式(3)可知，由于机身阻力与旋翼后向力均随前飞速度增加而增大且旋翼轴前倾角保持不变，所以旋翼迎角也在随速度增大。而旋翼迎角的增大使得直升机俯仰角更加前倾。

图10为飞行实测的俯仰角随前飞速度变化关系曲线(俯仰角抬头为正，低头为负)。从图10可看出，俯仰角随前飞速度的增加而更加前倾，可见实测结果是符合理论分析的。

图10 俯仰角随前飞速度变化关系曲线Fig.10 Relation curve of pitch angle with forward flight speed

2.2 侧倾角随前飞速度变化关系

图11为飞行实测的侧倾角随前飞速度的变化关系曲线(侧倾角左倾时为负，右倾时为正)。侧倾角呈现明显的随前飞速度增加先减小后增大的变化关系。

图11 侧倾角随前飞速度变化关系曲线Fig.11 Change curve of roll angle with forward flight speed

将图9各力投影到机体坐标系y轴上，则有

Fy,V+Fy,tr-Gcos(-θ)sinγ=0

(4)

因为γ为小量，所以旋翼侧倾角的表达式为

(5)

式(5)中：γ为旋翼侧倾角；Fy,V、Fy,tr分别为垂尾侧向力、尾桨拉力在体轴系y轴的分量。

由式(5)可知，影响侧倾角的主要是垂尾侧向力和尾桨拉力。图12可以看出，直升机起初向左倾斜，这是驾驶员为了保持直升机平衡，左压杆使直升机左倾斜以平衡尾桨拉力所引起的直升机右倾斜。随着前飞速度的增加，旋翼需用功率降低，平衡旋翼反扭矩的尾桨拉力也随之降低，当然侧倾角也应减小；随着前飞速度进一步增大，尾桨拉力和垂尾侧向力的快速增大，需要增大倾斜角以维持直升机的平衡，可见实测结果是符合理论分析的。

2.3 纵向周期变距随前飞速度变化关系

图12给出了飞行实测的纵向周期变距随前飞速度变化关系曲线。从图12可以看出，纵向周期变距随着前飞速度的增加而增大。

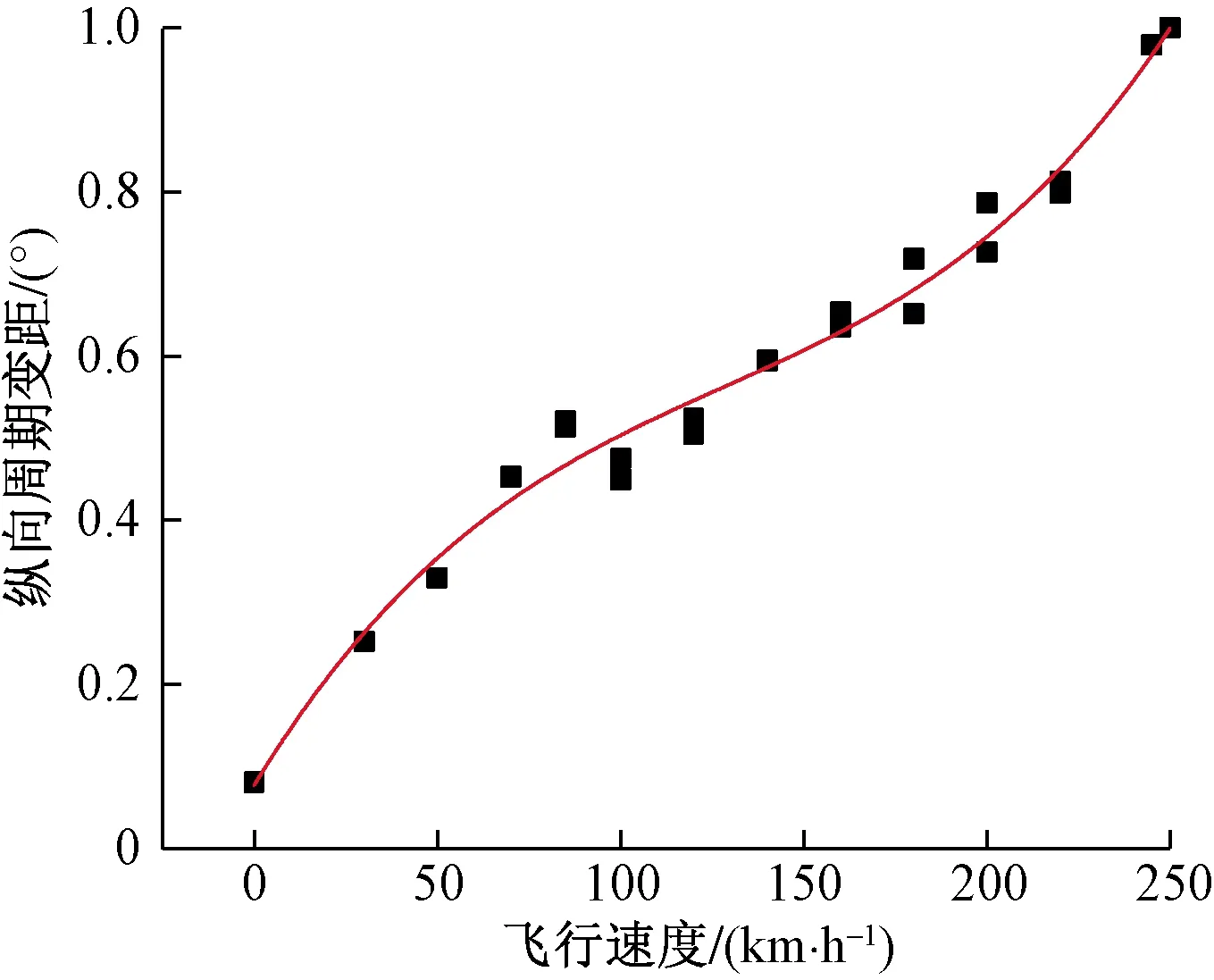
图12 纵向周期变距随前飞速度变化关系曲线Fig.12 Relation curve of longitudinal periodic pitch with forward flight speed

将图9中的各力投影到水平面，可得

T(-α1s-αs)=Fx,F

(6)

将α1s=α10-B1代入式(6)，则

T(B1-α10-αs)=Fx,F

(7)

式中：T为旋翼拉力；B1为纵向周期变距；α1s为旋翼挥舞后倒角；α10吹风引起的旋翼挥舞后倒角。

由于机身阻力和旋翼挥舞后倒角随前飞速度增加而增大，此时桨尖平面越来越后倒，产生越来越大的抬头力矩，为了克服阻力，保持平衡，这就要求驾驶员增大纵向周期变距，使自动倾斜器不断往前倾，以实现提升前飞速度。可见实测结果是符合理论分析的。

2.4 横向周期变距随前飞速度变化关系

图13为横向周期变距随前飞速度变化关系曲线。从图13可以看出，横向周期变距在小速度时，是增加的；在大速度时，是减小的。

图13 横向周期变距随前飞速度变化关系曲线Fig.13 Relation curve of lateral periodic pitch with forward flight speed

横向周期变距与旋翼的横向挥舞系数、尾桨拉力、垂尾侧向力等因素有关。由于在小速度范围内，直升机横向挥舞系数随速度的增大而增大，尽管尾桨拉力和垂尾侧向力由大变小，但此时横向挥舞系数占主导地位，所以横向周期变距是增大的。而在中间速度时，横向挥舞系数和尾桨拉力均在减小，此时横向周期变距缓慢减小；但随着前飞速度的进一步增大，尾桨拉力和平尾侧向力的剧增，需要使横向周期变距增大，以保持直升机平衡，可见实测结果是符合理论分析的。

2.5 总距随前飞速度的变化关系

图14为飞行实测的总距随前飞速度变化关系曲线。从图14可以看出，总距随前飞速度增加先减小后增大，呈马鞍形。

图14 总距随前飞速度变化关系曲线Fig.14 Relation curve of collective pitch with forward flight speed

总距φ7的表达式为

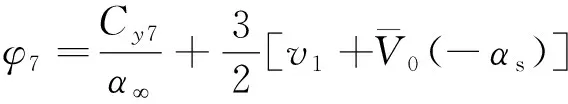
(10)

式(10)中：λ1为旋翼入流比；α为桨叶翼型升力系数；Cy7为桨叶0.7R处翼型升力系数，R为旋翼桨叶的半径；v1为诱导速度；为直升机质心处速度。式(10)的第一项近似为常数，那么，总距φ7随前飞速度的变化与诱导速度和前飞速度有关。

由于旋翼拉力不变时，随飞行速度的增加，诱导速度减小，桨叶典型剖面的来流角随之变小，为了保持一定拉力，迎角应保持不变，那么总距随之减小。当前飞速度大于久航速度后，由于直升机旋翼桨盘向前倾斜，使桨叶剖面来流角增大，为了保持拉力不变，必须增加旋翼总距，因此，总距随前飞速度的变化规律类似平飞需用功率随前飞速度的变化，呈马鞍形，可见实测结果是符合理论分析的。

2.6 尾桨距随前飞速度的变化关系

图15为尾桨距随前飞速度变化关系曲线。从图15可以看出，尾桨距随前飞速度的增加先减小后增大，呈马鞍形。

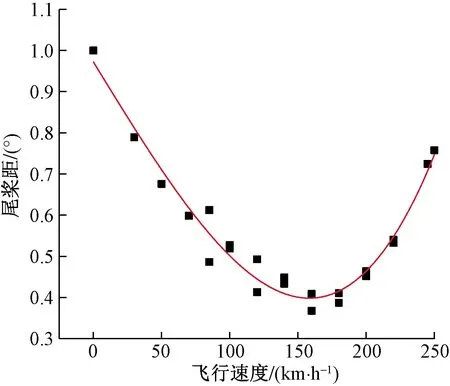
图15 尾桨距随前飞速度变化关系曲线Fig.15 Relation curve of tail rotor collective pitch with forward flight speed

尾桨通过其拉力平衡旋翼产生的反扭矩，旋翼的反扭矩随前飞速度变化呈马鞍形，这就要求尾桨拉力随速度的变化也要呈马鞍形。由于尾桨相当于垂直放置的旋翼，其入流速度的变化应与旋翼入流速度的变化相同，这样势必要求尾桨总距随前飞速度的变化关系呈现马鞍形。但是随着前飞速度的增加，垂尾产生的气动力可以帮助尾桨平衡旋翼的反扭矩，且速度越大，效果越明显，这时尾桨距在大速度时不像旋翼总距那样增加很快，可见实测结果是符合理论分析的。

3 载荷特性分析

3.1 旋翼载荷特性分析

3.1.1 随前飞速度变化关系

因旋翼桨叶6个剖面的挥舞弯矩、摆振弯矩飞行实测结果随前飞速度变化关系是一致的，这里仅以桨根剖面挥舞弯矩、摆振弯矩的动态分量随前飞速度的变化关系曲线为例予以说明，如图16所示。

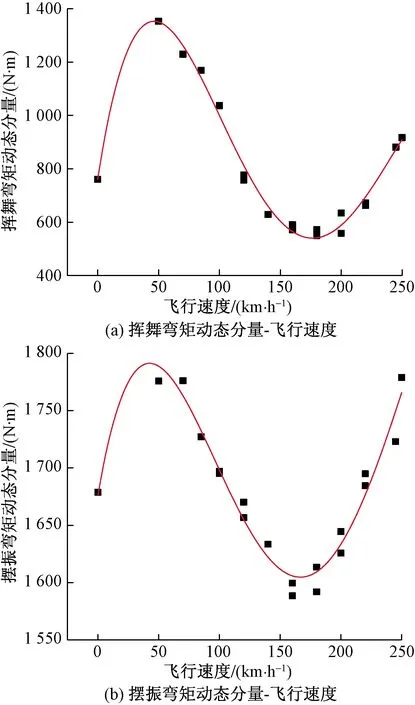
图16 挥舞弯矩、摆振弯矩动态分量随前飞速度变化关系曲线Fig.16 Relation curves of dynamic component of flap bending and lag bending moment with forward flight speed

从图16可以看出，挥舞弯矩与摆振弯矩的动态分量随前飞速度的变化关系曲线基本一致，都是随前飞速度增加是先增大后减小再增大。在小速度时，由于旋翼挥舞系数随前飞速度的增加是增大的，且旋翼自身的下洗流与机身之间的存在严重的气动干扰，这也是导致旋翼桨叶载荷增大的主要原因；但随着前飞速度继续增大直至久航速度区域时，由于旋翼诱导速度减小，旋翼需用功率减小而且此时旋翼流场与机身之间的干扰也在减弱，使得载荷动态分量相比小速度时有所减小；随着速度继续增大，旋翼左右气流不对称现象进一步加剧，旋翼需用功率和纵向周期变距的继续增大，导致桨叶挥舞、摆振弯矩随速度增加而增大。可见实测结果是符合理论分析的。

图17为旋翼桨叶剖面扭矩及变距拉杆轴向力的动态分量随前飞速度变化关系曲线。从图17可以看出二者变化规律是一致的。分析认为桨叶剖面扭矩是由变距拉杆轴向力经摇臂传递至桨叶产生，二者处在同一传力链路上，其变化规律同步的是符合理论分析的。

图17 扭矩和变距拉杆轴向力动态分量随前飞速度变化关系曲线Fig.17 Relation curve of dynamic component of torque blade and axial force of pitch link with forward flight speed

从图17还可以看出，二者变化曲线与总距变化曲线类似，呈马鞍形。这是因为总距的变化是通过变距拉杆来实现的，其在桨叶上以总距、扭矩变化来呈现，在变距拉杆上以轴向力变化来呈现。由于在小速度区域，受桨叶挥舞系数及气动干扰的影响，桨叶挥舞弯矩较大，引起桨叶剖面扭矩及变距拉杆在小速度区间载荷变大，而不是减小，这是桨叶挥舞运动与变距运动之间的耦合所造成的。

3.1.2 沿展向位置变化关系曲线

图18为旋翼桨叶挥舞弯矩、摆振弯矩动、静态分量沿桨叶展向位置变化关系曲线。由于挥舞弯矩、摆振弯矩与桨叶对应方向弹性挠曲变形是直接相关的，从图18可以看出，挥舞弯矩动态分量沿展向位置变化关系反映了桨叶挥舞方向前4阶固有振型变化特点，摆振弯矩动态分量沿展向位置变化关系反映了摆振方向前2阶振型变化特点。可见实测结果是符合理论分析的。

图18 挥舞弯矩和摆振弯矩动态分量沿展向位置变化关系曲线Fig.18 Relation curve of dynamic component of flap bending and lag bending moment along the spanwise position

3.1.3 沿方位角变化关系曲线

图19为3种速度下挥舞弯矩与摆振弯矩随方位角变化关系曲线。从图19可以看出，不同速度不同剖面挥舞弯矩、摆振弯矩沿方位角变化关系基本一致。大速度相比于小速度，挥舞弯矩、摆振弯矩沿方位角变化曲线比较“干净”。这是由于速度越小，旋翼尾流在斜后方(0°～270°)与机身之间的气动干扰越严重，给旋翼附加了周期的气动载荷，进而引起桨叶挥舞弯矩、摆振弯矩高频响应。但随着速度增加，旋翼尾流远离机身，这种高频成分逐渐就减弱了和消失了，曲线自然而然也就“干净”了。

图19 不同速度下的挥舞弯矩和摆振弯矩沿方位角变化关系曲线Fig.19 Relation curve of flap bending and lag bending moment along azimuth angle under different speed

由于挥舞弯矩都是由气动载荷和惯性载荷引起的，当气动载荷与惯性载荷同向时，出现波谷；反向时，出现波峰。在方位角0°时，气动载荷与惯性载荷同向(挥舞弯矩上挥为负)，由于弹性响应滞后于激励作用，因此在60°附近出现波谷；在180°由于气动力减弱且与惯性载荷反向，其波谷值减弱。90°附近的波谷与270°附近的峰值相对应，由于桨叶在这两个方位角处的惯性载荷是反向的，且90°时桨叶上挥与气动载荷同向，270°附近桨叶下挥与气动载荷反向，导致90°附近的挥舞弯矩大于270°附近的挥舞弯矩。

摆振运动是桨叶在离心力场中做挥舞运动产生的连带结果，尽管存在气动力及减摆器等因素的影响。但其整体呈现5次谐波的成分比较突出。这是由于摆振二阶频率即弹性一阶摆振频率比为5.5，因此5次谐波成分占优。

3.2 尾桨载荷特性分析

图20为尾桨叶挥舞弯矩、摆振弯矩、扭矩的动态分量随前飞速度变化关系曲线。从图20可以看出，在小速度时，尾桨载荷的动态分量随前飞速度增加而增大，随着速度增大至久航速度附近时，增长趋势减缓，随着速度进一步增大，增长趋势较快。分析认为这是由于在小速度时，尾桨挥舞系数较大，相比于悬停状态时，尾桨挥舞弯矩、摆振弯矩、扭矩有所增大是必然的。但随着速度继续增大，由于尾桨拉力在减小，导致尾桨挥舞弯矩、摆振弯矩、扭矩增长趋势减缓；随着前飞速度的进一步增大，尾桨需用功率的提高以及旋翼尾迹的影响，挥舞弯矩、摆振弯矩和扭矩快速增大，可见实测结果是符合理论分析的。

图20 挥舞弯矩、摆振弯矩和扭矩动态分量沿方位角变化关系曲线Fig.20 Relation curve of dynamic component of flap bending, lag bending and torque blade of section with forward flight speed

3.3 旋翼轴载荷特性分析

图21为旋翼轴扭矩随前飞速度变化关系曲线。从图21可以看出，旋翼轴扭矩变化关系与平飞需用功率曲线基本是一致的，呈马鞍形。分析认为：由于旋翼需用功率与旋翼轴扭矩成正比，且旋翼需用功率系数基本是一个常值。所以，旋翼轴扭矩与发动机输出功率随前飞速度的变化关系曲线应是一致的，呈马鞍形。可见实测结果是符合理论分析的。

图21 旋翼轴扭矩随前飞速度变化关系曲线Fig.21 Relation curve of rotor shaft torque with forward flight speed

3.4 垂尾弯矩特性分析

图22为垂尾弯矩随前飞速度变化关系曲线。从图22可以看出，垂尾弯矩随前飞速度增加是先减小后增大。分析认为：垂尾弯矩的产生主要由两部分力产生的，一个是尾桨拉力，一个是垂尾侧向力，由于在小速度时尾桨拉力是由大变小的，且垂尾的侧向力此时很小，所以在小速度时垂尾弯矩的变化趋势是减小的；但随着速度的增加，尾桨拉力及垂尾侧向力的增大，垂尾弯矩也会由减小趋势转为增大趋势，且随着速度的增加，增大得越快。可见实测结果是符合理论分析的。