改进天牛须搜索优化神经网络的港口货运量预测
2021-04-13廖列法欧阳宗英
廖列法, 欧阳宗英
(江西理工大学信息工程学院, 赣州 341000)
近年来中国进出口贸易加快发展,而港口作为贸易重要枢纽之一、全球贸易的重要设施以及国际物流链上的重要节点[1],其战略地位和作用不言而喻。作为全球资源配置的重要手段,港口物流大大加快经济全球化和贸易一体化的进程,并且极大地促进了港口腹地经济快速增长和腹地贸易扩张。港口货运量预测对港口的建设发展具有极其重要的意义。科学且有效地预测港口货运量,能为港口和其腹地城市经济的发展提供有利的决策信息,从而正确指导港口规划建设和引导其进一步发展转型。因此,对港口货运量进行精准预测成为中外学者的研究热点。
目前,中外学者对港口货运量预测进行了大量的研究,总结出了一系列有效的预测方法。文献[2]建立基于TEI@I方法论的港口物流货运量模型,对青岛港的集装箱吞吐量进行分析预测。文献[3]利用蝴蝶极限学习机(butterfly extreme learning machine,BELM)技术对从变分模式分解获得的每个组件进行建模和预测,建立基于训练误差序列的BELM预测模型,以预测随后的误差。文献[4]基于7种机器学习算法和小波分析建立了预测模型,对天津港货物吞吐量进行预测。
随着神经网络技术的大力发展,也有许多学者将神经网络技术带入货运量的预测中[5-7]。文献[8]建立了反向传播神经网络模型,来预测上海港和连云港港的集装箱吞吐量,并与灰色模型、三重指数平滑模型和多元线性回归模型进行对比。文献[9]把港口货物分成37种,结合神经网络对香港港的货物吞吐量进行精准预测。文献[10]用不同的方法构建并训练神经网络,对时间序列进行预测分析。文献[11]分别将ARIMAX(autoregressive integrated moving average with explanatory variable)模型和 Holt-Winters 模型与神经网络结合,应用于连续时间序列的预测。文献[12]建立了基于SARIMA(autoregressive integrated moving averages) 模型和人工神经网络的时间序列组合预测模型。文献[13]采用BP(back propagation)神经网络对货物吞吐量的子序列进行预测。文献[14]利用灰色模型和BP神经网络构建了灰色神经网络模型,提升了预测精度。文献[15]利用Elman神经网络来预测,并于BP与RBF(radical basis function)进行对比。文献[16]通过改进BP神经网络的网络结构来预测未来3年的吞吐量。
上述神经网络预测模型并未考虑众多内在、外在因素对货运量的影响。现针对受众多复杂因素影响的港口货运量,首先初步建立港口货运量预测评估体系,再提出一种基于天牛须搜索(beetle antennae search, BAS)算法改进的Elman神经网络预测模型。用该模型对港口货运量进行预测分析。
1 典型影响因素分析
随着经济全球化进程的进一步发展,影响港口货运量的因素也逐步增多,主要分为内在因素、外在因素以及技术因素[17]。内在因素主要有港口间的客户竞争、客户削减成本和追求高水平服务以及港口的内在发展等。外在因素有腹地经济发展、腹地工业发展水平、腹地居民消费水平以及腹地基础设施完善性等。技术因素为集装箱标准化运输和码头的智能化管理等。但中国对于港口货运量的典型影响因素的选取还未形成统一的体系。
1.1 港口货运量影响因素
针对腹地经济水平、腹地消费水平、腹地集疏运能力、腹地进出口贸易和港口货运能力5个方面,选取其中13个重要影响因素指标作为港口货运量X0的影响因素。13个指标如表1所示。

表1 重要影响因素指标Table 1 Important impact factor indicators
1.2 数据归一化和主成分分析
收集了上海1989—2018年X1~X13各30组数据,共计420条数据,其数据来源于《上海统计年鉴》[18]以及国家统计局《上海市年度数据》[19]。由于选取的影响因素较多且各数据量纲不一,为避免信息冗余,提升数据处理效率,统一量纲,对各项数据进行归一化处理和降维处理。具体步骤如下。
1.2.1 零-均值规范化
由于影响因素量纲不尽相同,所以首先对数据进行归一化处理,即
(1)

1.2.2 相关性检验
对归一化后的数据进行相关性检验,如表2所示。从表2中可以看出,各因素间的相关程度比较高。

表2 各因素相关性系数Table 2 Correlation factor
1.2.3 主成分分析
为了消除各因素之间的相关性,采取主成分分析法对数据进行分析。根据相关性检验所得的相关系数建立特征方程,求得特征值和特征向量,最后根据特征值和特征向量求得方差贡献率和累计方差贡献率。所求相关数据如表3所示。
1.2.4 主成分选取
为减小信息冗余对数据的干扰,一般选取累计方差贡献率>85%的且特征值大于1的前k个成分作为主成分,即保留前k个主成分就能充分反映原始变量的绝大多数信息。分析表3数据可得,选择影响因子累计方差贡献率93.86%且特征值为12.202的因素作为主成分。

表3 各因素特征值和方差贡献率Table 3 Eigenvalue and variance contribution rate of each factor
计算主成分荷载矩阵,计算结果如表4所示。表4显示GDP(X1)、第一产业增加值(X2)、第三产业增加值(X4)、居民消费水平(X6)、社会消费品零售总额(X7)、总货运量(X9)和港口万吨级泊位数(X13)占主成分的荷载较大,与主成分相关程度相对较高。最后取这7个与主成分相关程度高的影响因素作为输入变量,如表4中带“*”号数值。
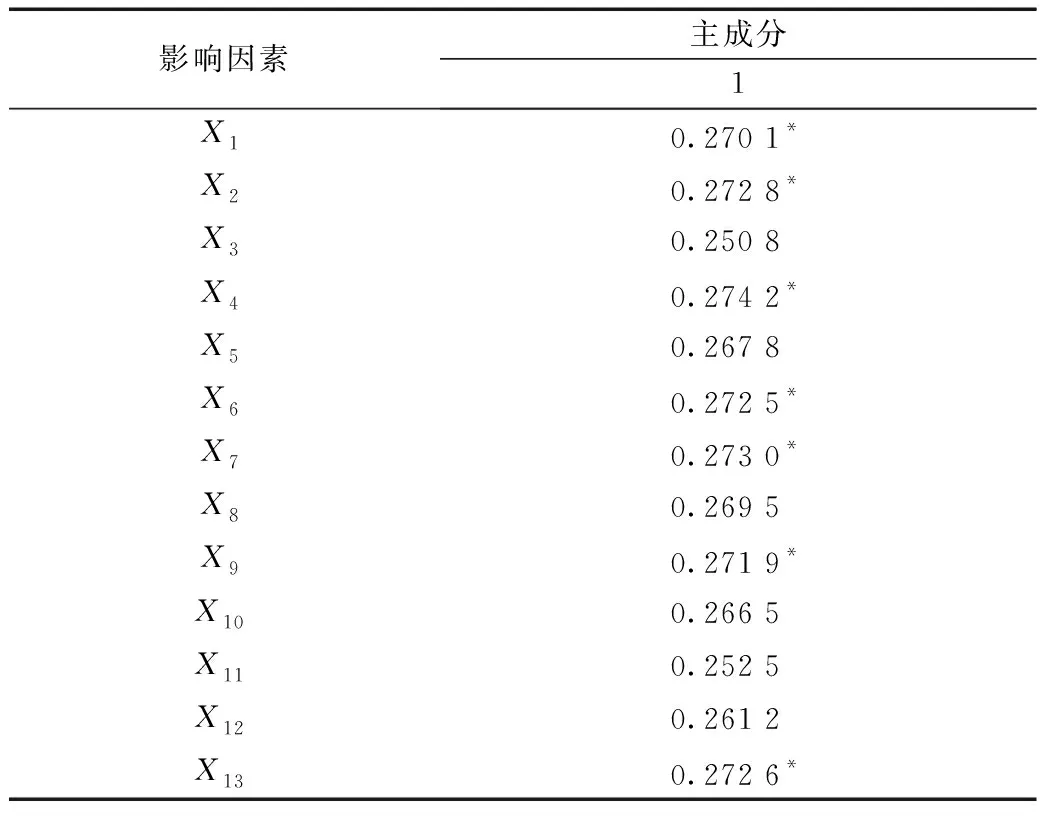
表4 主成分荷载矩阵Table 4 Principal component load matrix
2 算法分析
2.1 BAS算法
BAS[20-21]是2017年提出的仿天牛觅食行为的新型优化算法,该算法易理解,且运算量小、寻优速度快。其基本原理为:天牛在觅食时,不知道食物的位置,利用左右触须来分辨食物气味的浓度,如果左触须感受到的气味浓度高则天牛向左移动,反之向右移动,最后寻找的食物的位置即最优值。而天牛搜寻食物的过程就是天牛须算法的寻优过程。BAS与其他智能算法相比,只需单个个体,大大加快了搜索速度,也不需要具体函数和梯度信息,就能实现寻优过程。其主要步骤如下:
(1)天牛初始朝向创建:
(2)
式(2)中:rands(·)为随机函数;k为空间维度。
(2)建立天牛左右须坐标:
(3)
式(3)中:xleft表示左须的位置坐标;xright表示右须的位置坐标;xt表示迭代次数为t时天牛的质心坐标;d0为两触须之间长度,其值应足够大以覆盖适当的搜索区域,以便在开始时跳出局部最小点;n为总迭代次数;t为当前迭代次数。
适应度函数f(·)则用来判断左右须气味浓度,即f(xleft)和f(xright)的大小。f(·)根据实际需求定,对适应度函数的选取将在2.4节详细阐述。
(3)更新天牛的位置,比较左右触须的适应度大小,若f(xleft)>f(xright),天牛向左移动;反之,向右移动。其公式为
(4)
式(4)中:ξt表示t次迭代步长因子;sign(·)为符号函数。
2.2 算法改进
研究发现,天牛的初始朝向会对收敛速度产生一定的影响,因此引入Laplace分布来确定天牛的初始朝向。相比较均匀分布产生随机数的方法,使用 Laplace 分布产生随机数更有利于探索搜索空间,发现新的潜在解。Laplace分布概率密度函数为

(5)
其分布函数为
(6)
本文中r∈(-,+)是位置参数,s>0是尺度参数,x为空间维度。在多维空间中,天牛在当前位置根据评价函数来感应下一步的位置,此时容易陷入局部最优[22],因此引入模拟退火算法(simulate anneal,SA)。将SA的蒙特卡洛准则引入,使天牛跳出当前局部最优。具体步骤为
(7)
式(7)中:ρ为转移接受概率;f(xt)为当前位置的适应度值;f(xt-1)为前一位置的适应度值;T为当前温度,T随迭代次数不断递减,选取线性递减系数eeta=0.92。
2.3 Elman神经网络
Elman神经网络分为4层[23],除常见的输入层、隐含层和输出层外,还有1个特殊的承接层,其结构如图1所示。
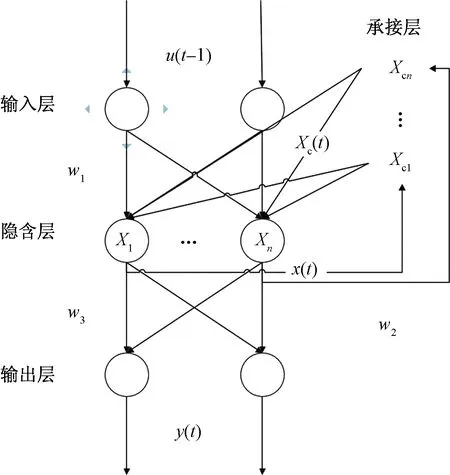
图1 Elman神经网络结构Fig.1 Elman neural network structure
由图1可看出,Elman神经网络比BP等前馈神经网络增加了承接层,主要作用是存储隐含层前一时间的输出数据,将其返回给该网络输入,以此来加强网络的动态信息处理能力。参照图1中Elman神经网络的结构模型,其输入、输出关系为
(8)
式(8)中:x为隐藏层向量;y为输出向量;u为输入向量;xc为承接层反馈向量;w1为输入层至隐含层连接权值;w2为承接层到隐含层的连接权值;w3为隐含层至输出层连接权值;g1(·)为隐含层传递函数;g2(·)为输出层传递函数;t为时刻。
2.4 LBAS-Elman神经网络模型建立
将改进的天牛须算法优化Elman神经网络的初始权值和阈值,并将其应用到已经设定好的网络中,从而构造出最终的训练模型。通过这种方法构造的模型能克服标准Elman神经网络收敛速度慢和预测精度低等问题。模型建立步骤如下。
(1)利用Laplace分布来创建天牛的朝向向量。利用式(5)、式(6)则可以得到天牛的初始位置朝向:
x=Laplace(k;r,s)
(9)
式(9)中:Laplace(k;r,s)为Laplace分布;k为空间维度;r∈(-,+)为位置参数;s>0,为尺度参数,函数h始终关于r对称,且在[0,r]上递增,[r,+]上递减。
(2)设置步长因子ξ。天牛的区域搜索能力由ξ决定,为了提高天牛的搜索范围,选取了较大初始步长,并线性方式递减步长,公式为
ξi+1=ξieeta,i=1,2,…,n
(10)
(3)评价指标的指定。选取式(11)作为该模型的评价函数。
(11)
式(11)中:dfi为第i个样本模型输出值;dvi为第i个样本实际值。
(4)更新天牛位置。根据式(4)来更新天牛下一步的位置。并采用式(7)加快算法跳出局部最优。
(5)更新解。根据天牛更新后的位置,求出该位置左右须的适应度函数,利用式(4)更新天牛的位置,即调整Elman神经网络的阈值和权值。再将当前位置适应度值与当前最优进行对比,若当前位置适应度值更优,则更新,反之,则不更新。
(6)最优解生成。当算法迭代停止时,最后得出的最优解即为整个训练的最优解。
综上所述,LBAS-Elman神经网络模型的流程如图2所示。
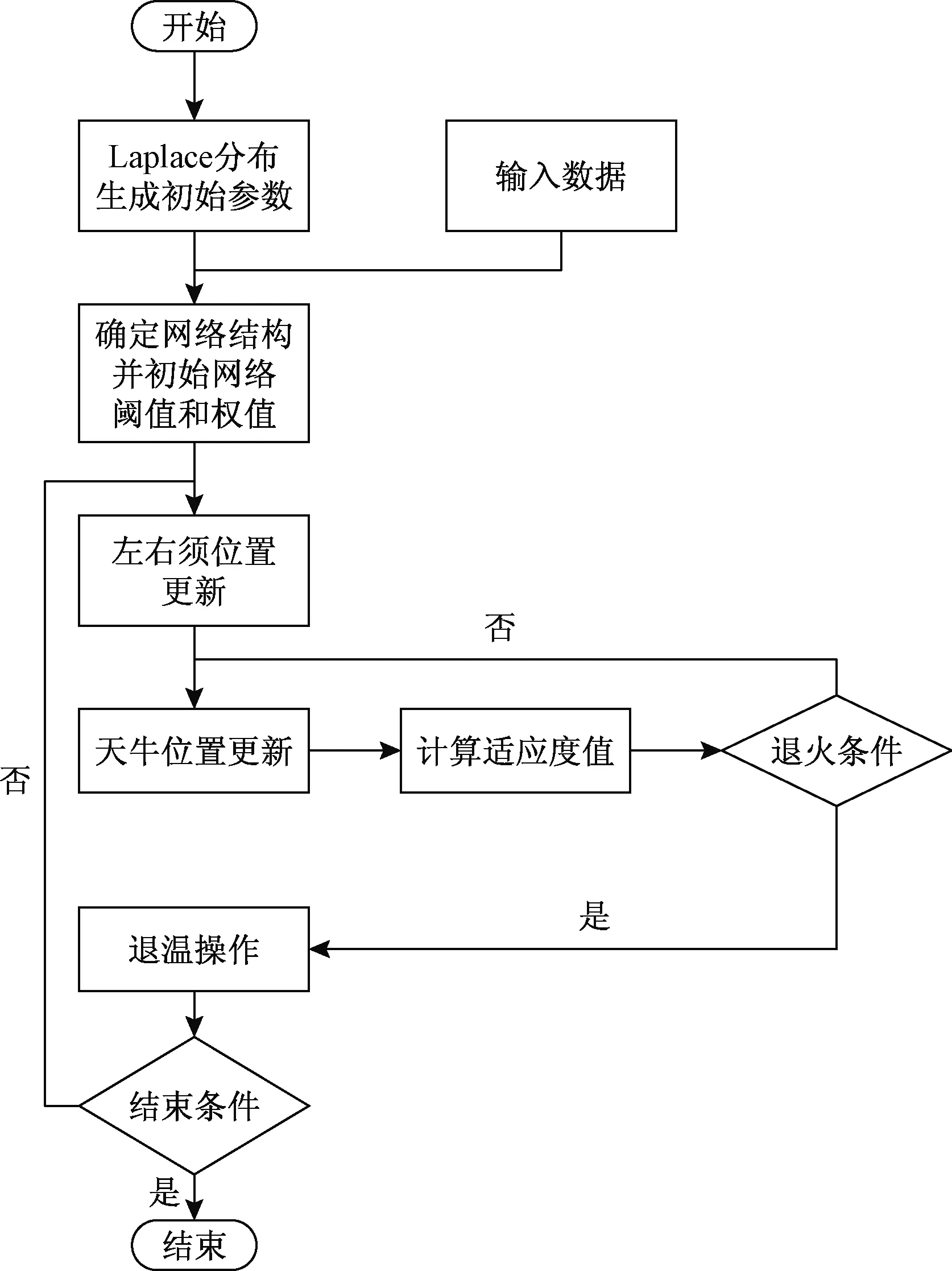
图2 LBAS-Elman神经网络模型流程Fig.2 LBAS-Elman neural network model flowchart
3 货运量预测
3.1 数据选取
港口吞吐量的决定因素有很多,经过分析得到典型影响因素有7项:GDP(X1)、第一产业增加值(X2)、第三产业增加值(X4)、居民消费水平(X6)、社会消费品零售总额(X7)、总货运量(X9)和港口万吨级泊位数(X13)。
自上海统计局和国家统计局收集了上海1989—2018年30年的7项典型因素数据以及港口吞吐量数据,共计30组数据。将此8项数据进行分析和整理,以前25组连续数据组成训练集,后5组连续数据组成测试集。以7项典型因素的数据作为输入数据,港口的吞吐量数据作为输出数据,以此构成数据样本表。2014—2018年的各项数据可以生成5组样本数据,如表5所示。

Sunrise reddens the sky in the morning, clouds impending and autumnwind will blow; sunset concentrated in a corner of sky, autumn-breed is on the horizon.”

表5 2014—2018年典型影响因素样本Table 5 Sample of typical influencing factors from 2014 to 2018
3.2 仿真实验
以MATLAB 2018a为平台,Elman神经网络则运用其自带神经网络工具箱。改进天牛须搜索算法的空间维度k=82,步长因子ξ=20,迭代次数n=100。
为检测LBAS-Elman神经网络模型预测的性能,选取相对误差E、相关系数R2作为评价指标来全方位地评价该模型的性能[24]。评价指标计算公式为
(12)
(13)
式中:n为迭代次数;N为训练集样本数量;dfi为第i个样本模型输出值;dvi为第i个样本实际值。且相对误差越小,说明模型性能越好;决定系数的范围在[0,1]内,如果R2愈接近于1,表明模型性能愈好,反之,R2愈趋近于0,表明模型性能愈差。
3.3 结果分析
为了测试天牛须算法与其他智能算法的优化效果,设计了Elman、PSO-Elman、GA-Elman模型、BAS-Elman模型、LBAS-Elman模型。经过反复多次试验,结果如图3、图4所示。图3所示为初始步长为20时,LBAS-Elman 模型的适应度值变化曲线。图4所示为不同优化算法优化Elman神经网络得到的适应度值变化曲线。由图3、图4可知,LBAS-Elman 模型在迭代次数为6时,就能找到适应度最优值,而BAS-Elman模型、PSO-Elman模型和GA-Elman 模型分别需要22、35、39次迭代才能找到最优值。由此可知提出的LBAS优化算法收敛速度较其他优化算法显著提高。
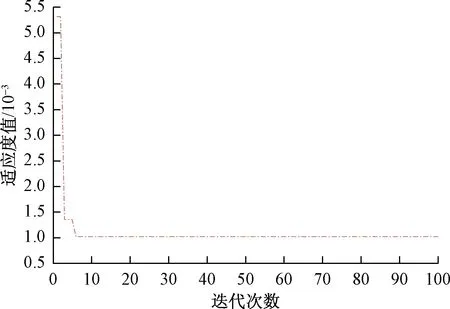
图3 LBAS-Elman神经网络模型适应度曲线Fig.3 Fitness curve of LBAS-Elman neural network model

图4 各优化算法网络模型适应度曲线对比Fig.4 Comparison chart of fitness curves of network models of various optimization algorithms
图5和图6分别为Elman神经网络和LBAS-Elman 神经网络预测模型训练集的拟合结果,对比得出,显然LBAS-Elman优化模型所形成的预测曲线更加逼近实际值。

图5 Elman神经网络模型拟合结果Fig.5 Elman neural network model fitting results
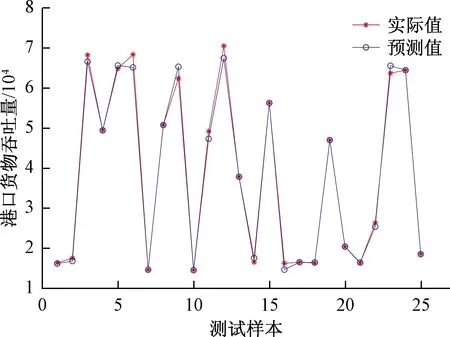
图6 LBAS-Elman神经网络模型拟合结果Fig.6 LBAS-Elman neural network model fitting results
LBAS-Elman模型与其他4个模型预测相对误差对比如图7所示。从图7中可以看出通过 Elman 神经网络预测的结果与实际值之间的相对误差最高接近0.23,而且集中在0.1~0.15。GA-Elman模型和PSO-Elman模型则比未优化的Elman模型要更好,但最高相对误差也均达到0.15,而LBAS-Elman模型的相对误差则大多集中在0~0.05,LBAS-Elman 的预测精度相对其他优化模型有较大的提升。

图7 LBAS-Elman与其他模型预测相对误差Fig.7 Relative error of LBAS-Elman and other models
为了测试天牛须算法与其他智能算法的优化效果,设计了Elman、PSO-Elman、GA-Elman模型、BAS-Elman模型和LBAS-Elman模型。分别从相对误差、相关系数、迭代次数、收敛时间来对模型的精度进行描述。为了准确性,对5个模型都进行50次实验,分别取其平均值。
表6所示为各模型效果对比。从表6中可以看出,LBAS-Elman、BAS-Elman和PSO-Elman模型相对误差都较低,且相关系数都达到了90%以上,其中LBAS-Elman模型甚至达到99.09%,而GA-Elman 模型的效果相比前三者都要差,并且其迭代次数和收敛时间都是四者里最高的。LBAS-Elman和PSO-Elman模型以及BAS-Elman模型相差不大,但LBAS-Elman网络模型的训练速度以及精度都要高于PSO-Elman和BAS-Elman网络模型。所以综合相对误差、相关系数、迭代次数以及收敛时间4个因素分析,LBAS-Elman网络效果最佳,这体现了LBAS-Elman预测模型在货物吞吐量预测方面具有良好的适用性。

表6 各模型的效果对比Table 6 Effect comparison of each model
4 结论
提出一种基于改进天牛须的优化Elman神经网络模型,使用改进后的神经网络权值和阈值,对港口货物吞吐量进行预测。相比于传统的Elman神经网络,其优化后的权值和阈值明显优于随机生成的权值和阈值,且在对港口吞吐量的预测中,LBAS-Elman 模型预测精度有明显的提高。且相对其他优化算法,具有收敛速度快、精度高等优点。
在经济全球化大背景下,全球进出口贸易不断提升,而港口作为外贸的重要枢纽之一,其作用愈发重要,LBAS-Elman模型,对港口吞吐量预测精度有较大的提升,这有利于港口管理者对港口的掌控和监管,也能加快传统港口的转型升级的步伐和智慧港口的建设,以此适应新一轮的经济发展。
