基于单目视觉的矩形靶面弹着点测量
2021-04-11王海亮陈登旭黄晓慧
王海亮,陈登旭,刘 吉,王 鹏,黄晓慧
(1.中北大学 信息化建设与管理处,山西 太原 030051;2.中北大学 信息与通信工程学院,山西 太原 030051)
引言
弹点位置测量广泛应用于武器性能参数测试,如射击精度、密集度试验,检验被试枪弹密度是否满足战术指标要求。另外,检验弹道一致性也需要测量弹着点分布。传统弹着点测量是通过人工判读,精度容易受人为因素和测量工具影响,且时效性低[1-2]。目前的主要方法有线圈靶、光幕靶[3-5]、声电靶[6]、CCD 光电靶[7-8]等,这些测试手段提高了测量的精度,效率以及自动性。上述方法虽然自动化程度很高,但所需设备复杂,成本比较高,而且测试设备容易受到弹丸的破坏,并且这些测量方法受外界环境影响测量误差也会增大。基于单目视觉技术的弹着点坐标测量方法设备简单,只需要一台相机即可,同时精度、效率较高。该方法首先是通过张正友标定法[9]获得相机的内参,并且利用角点识别技术检测出图像中靶面4个角点位置,采用矩形P4P 方法[10-13]解出靶面坐标相对于相机坐标的位姿关系即外参;然后使用图像处理技术定位图片中弹着点的坐标;最后利用单目相机成像原理解出靶面弹着点的实际坐标。
1 单目视觉成像原理
1.1 相机成像坐标转换
相机成像过程涉及到了4个坐标系的转换,分别是图像像素坐标坐标系、图像物理坐标系、相机坐标系、世界坐标系。
相机采集的图片为数字图像,在计算机中以数组的形式储存,数组的每个元素为像素,值为灰度。如图1所示,定义坐标系O0uv为图像坐标系,O1XY为图像物理坐标系。O1是相机光轴与图片的交点,X、Y轴分别与u、v轴平行。

图1 图像像素坐标系和图像物理坐标系关系图Fig.1 Relationship between image pixel coordinate system and image physical coordinate system
2个坐标系的关系式为

齐次坐标和矩阵表示为
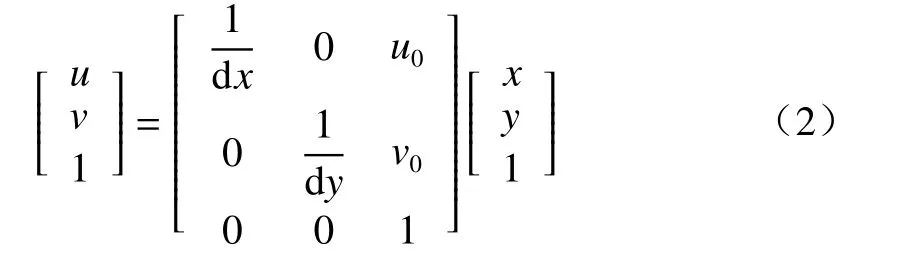
相机坐标系是以相机的光心Oc为坐标原点,Xc、Yc轴与图像物理坐标系的X、Y轴平行,Zc轴为相机光轴,垂直于图像平面。世界坐标系则是用来描述现实中物体的世界位置,用OwXwYwZw表示。假设世界坐标系中P(Xw,Yw,Zw)在相机坐标系中的坐标为(Xc,Yc,Zc),可以得到如下关系:

式中:R是3×3的正交单位矩阵,也称为旋转矩阵;t是三维平移向量。
1.2 相机成像模型
相机成像的基本模型是基于小孔成像原理的针孔模型,如图2所示。空间中点P经成像后在图像平面的投影点为Q,P、Q和相机光心在同一直线上。

图2 相机针孔成像模型Fig.2 Camera pinhole imaging model
假设P点在相机坐标系中的坐标为(Xc,Yc,Zc),则其投影点Q在图像坐标系下的坐标为(x,y),相机焦距为f,根据相似三角形原理得出:

用齐次坐标和矩阵表示上述关系得到(5)式:

式中:s为比例因子。
将(3)式和(5)式合并,得到最终的图像像素坐标系和世界坐标系的转换关系:
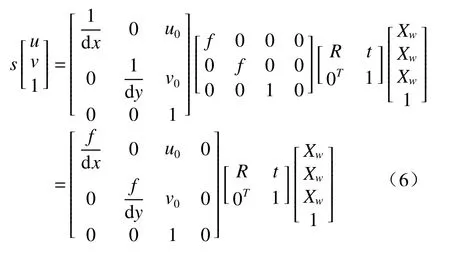
即:

式中:A为相机的内参矩阵;M为外参矩阵;H为图像坐标系与世界坐标系最终的映射关系:

则(7)式展开消除s得到:

该式为空间直线方程。并且可以看出一个像素点对应射线上任意一个空间点,因此不能通过单一像素点坐标求出空间坐标,但是由于我们测的是靶面弹着点坐标,定义世界坐标系的Xw、Yw刚好在靶面上且与靶面的边界平行,靶面的任何位置的Zw=0,即得到了平面Z的空间方程,结合(9)式可以求出点的二维靶面坐标。
2 图像特征点检测
图像中靶面4个角点和弹孔位置的识别是单目视觉测试的前提。图像特征是区分图像的依据,包括角点、直线、边缘和轮廓等,不同图像特征的识别有不同的方法。由于在实际靶面拍摄中,得到的图片中靶面与靶场背景灰度有差异,而Harris角点检测[14-15]是通过计算图像上移动窗口的灰度变化来定位角点,所以在本文4个靶面角点的识别采用的就是Harris角点检测法。首先将相机采集的图片进行灰度处理,如图3所示,使之成为我们所需要的灰度图片;接着将图片二值化,这样有利于去除不利于角点检测的灰度信息;利用Harris角点检测法检测角点,并提取出所需要的角点像素坐标。

图3 靶面原图Fig.3 Original image of target surface

图4 靶面图片的弹孔识别图Fig.4 Bullet hole identification diagram of target picture
3 相机参数获取
相机的内参采用张正友标定法来获取,只需要用相机拍摄已知尺寸的标定板在不同方向的多幅图像,通过获取的特征点的图像坐标和特征点的世界坐标计算出相机的内参。这种标定方法发展已经相对成熟,这里不做过多阐述。本文的关键点在于外参的获取,这里运用呈矩形分布的P4P问题的求解方法得到靶面的世界坐标系与相机坐标系的X轴和Y轴之间的位姿关系。
3.1 外参解算的数学模型
图5为外参测量示意图。

图5 外参测量示意图Fig.5 Schematic diagram of external reference measurement
1)靶面的边界角点P0、P1、P2、P3位于靶面上,分别在像面上对应q0、q1、q2、q3,P0P1P2P3为矩形,其中P0P1⊥P1P3,P0P1//P2P3,|P0P1|=l1,|P2P3|=l2;
2)P0、P1、P2、P3在靶面世界坐标下的空间坐标已知,q0、q1、q2、q3在图像坐标系下的像素坐标通过图像处理可得;
3)相机成像的内参矩阵A已知。
3.2 呈矩形分布的P4P 问题的求解
像平面上的靶面角点在相机坐标系下的坐标分别为q0(x0,y0,f)、q1(x1,y1,f)、q2(x2,y2,f)、q3(x3,y3,f),其中f为相机的焦距。设光心Oc与q2q3形成的平面是S1,由两条直线方程可以求出该平面S1的标准法向量N1,N1=(nx,ny,nz)T;又因为P0P1//P2P3,所 以分别是光心到靶面角点P0、P1的距离与光心到像点q0、q1的距离的比值。
由
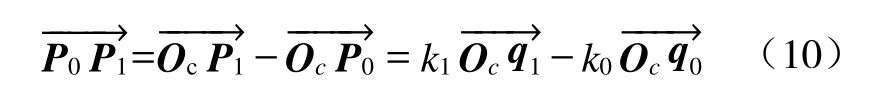
可得:
水工隧洞为了提高其抗渗性及抗冻性,一般选择硅酸盐水泥或普通硅酸盐水泥。在具体选择水泥时,主要比较水泥看其K2O和Na2O含量。在水工混凝土中,所选水泥其C3A含量不应大于8%,Na2O含量不应大于0.6%。在骨料选择时,应采用非碱或低碱活性骨料。水泥、骨料在使用前必须严格对其碱含量进行检测。

另外,由于|P0P1|=l1,可得:

联立(12)式和(13)式可以求出k0和k1。这样P0点在相机坐标系下的坐标便可以计算出来,即:P0(xp0,yp0,zp0)=(k0x0,k0y0,k0f),P1(xp1,yp1,zp1)=(k1x1,k1y1,k1f)。
P0作为世界坐标系的原点,它在相机坐标系下的坐标就是世界坐标系对于相机坐标系的平移向量,T=(xp0,yp0,zp0)T。世界坐标系的Xw轴在相机坐标系下的方向为
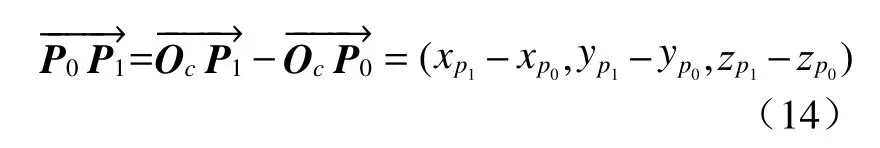
世界坐标系的Yw轴在相机坐标系下的方向为

将这2个向量标准化,得到(r11,r21,r31)和(r12,r22,r32),即为旋转矩阵R的第一列和第二列向量,世界坐标系的Zw轴在相机坐标系下的方向向量(r13,r23,r33)可由Xw,Yw在相机坐标系下的方向向量叉乘得到:

这样便得到旋转矩阵R,靶面坐标系相对于相机坐标系的外参便解算出来了。
4 试验分析
实验中采用的靶面大小为500 mm×500 mm,弹孔直径约8 mm。进行5个弹孔坐标的测量,实验流程如图6所示。

图6 弹着点坐标测量流程图Fig.6 Flow chart of impact point coordinate measurement
4.1 相机标定
调整好相机的镜头,拍摄18 张标定图片进行标定,如图7所示。

图7 相机内参标定示意图Fig.7 Schematic diagram of camera internal reference calibration
标定后相机的内参为

像素平均误差由图8可得最大投影误差仅为0.12像素,平均投影误差为0.05像素,达到了亚像素级别。
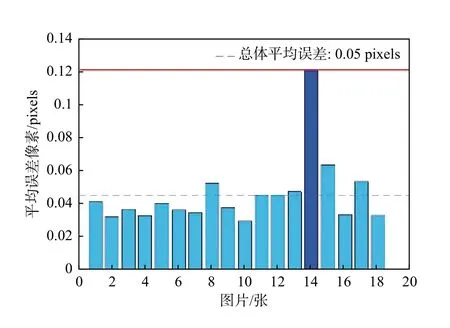
图8 相机标定的投影误差Fig.8 Projection error of camera calibration
4.2 弹孔坐标测量
图9为靶面与相机近似平行时的靶面图。

图9 靶面与相机近似平行时的靶面图Fig.9 Target surface diagram when target surface is approximately parallel to camera
当靶面与相机近似平行时,外参通过4个角点计算得到:

由此得到像素坐标和靶面世界坐标的映射矩阵为

当靶面与相机镜头平面近似平行时,用单目视觉测量弹孔坐标的实验结果如表1所示。
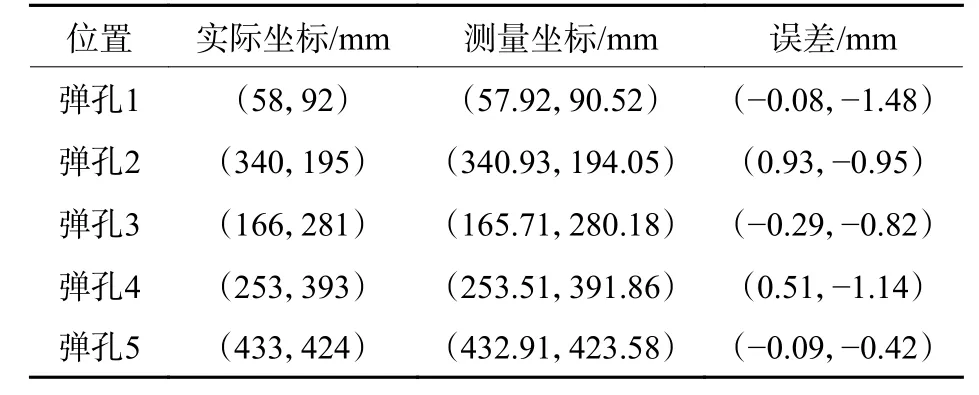
表1 靶面与相机近似平行时测量坐标及其误差Table1 Measuring coordinates and errors when target surface is approximately parallel to camera
但是实际的测量过程当中,靶面与相机镜头平面完全平行是很难做到的,总会与靶面存在一定的角度,如图10所示。将靶面与相机镜头平面调整一定的角度测量,测量结果如表2所示,可以看出即使存在角度,测量最大误差也在2.3 mm。

图10 靶面与镜头平面存在一定角度时的靶面图Fig.10 Target surface diagram when there is certain angle between target surface and lens plane

表2 靶面与相机存在一定角度时测量坐标及其误差Table2 Measuring coordinates and errors when target surface and camera have certain angle
5 结论
本文提出一种基于单目视觉的弹着点测量方法。利用图像处理技术识别出靶面4个角点以及弹孔位置,根据张正友标定方法和矩形P4P 问题的求解得到相机的内外参数,并且通过单目视觉原理测量处理弹着点坐标。最后结合实验数据分析,得出靶面与相机越接近平行测量精度越高。靶面与相机存在一定的角度,最大误差也在2.3 mm。充分证明了该方法是一种可行、有效、精度较高的弹着点测量方法。但是,在实际应用过程中光照条件、弹孔形状等可能会对测量精度产生影响,后续将进行这方面的研究,以便于该系统可以在实践中得到广泛应用。
