微小通道内低Reynolds数液-液两相流动与换热特性实验研究

2021-04-09王长亮田茂诚

化工学报 2021年3期

王长亮，田茂诚

（山东大学能源与动力工程学院，山东济南250061）

引言

微流体装置作为微化学工业的核心在过去几十年中引起了广泛的关注。由于其结构紧凑、比表面积大、内部传输路径短、扩散率低而具有优异的热和质转移能力[1]。在化学传质[2-4]、热交换器[5-6]、液滴生产和精细化学品/药物合成[7]等领域都有着广泛的应用。其中微通道内液-液两相流动在微化工系统中占据着重要的地位。实现对两相流流型、液滴长度等流体动力学参数的精确调控对微反应器的设计和优化，微换热器换热能力的提升具有重要意义。也正因为此，对于微小通道内液-液两相流水动力特性的研究开展时间较早，目前已有较为广泛的模拟和实验研究可以参考[8-13]。换热方面，由于微小通道内液-液两相换热系统有更小的体积、更高的传热速率和更稳定的运行条件，其在电子器件热管理、微通道两相热交换器和反应器等需要高热量传递的领域有着广阔的应用前景[14]。同时也是解决传统空气冷却和单相水冷却不能满足逐渐升高的热流驱散密度的首选方案[15]。但由于该方向开展时间较短，相关研究仍十分不足，理论体系更需完善。

弹状流（Taylor 流）是微小通道内液-液两相流的典型流型，同时也是实际应用中最常用的流型。连续相液体中气泡/液滴的存在改变了内部流场，形成内循环流动模式。这种流动模式促进了流体的径向混合，为强化传热提供了一种新的机制。近些年国内外有关气-液Taylor 流强化换热的研究逐渐增多，发现其传热系数相比单相水层流提高了约2～4 倍[16-17]。液-液弹状流中分散相和连续相均为液体，有相同的热容量阶数。相比气-液Taylor流中气体几乎不参与换热，液-液弹状流明显有更好的热驱散潜能。如果将其中一相更换为纳米流体或具有超强导热性的金属流体，这一优势将变得更加显著[18]。但截至目前有关液-液弹状流换热特性的研究却十分有限。Egan等[19]采用高分辨率红外热像仪对恒热流边界条件下圆管内液-液泰勒流的传热特性进行了实验研究，结果表明，相比单相流动换热性能提高了近600%，段塞长度和膜厚的变化对换热率有显著影响。Che 等[20]采用水平集方法对方形和矩形通道内水-矿物油体系的换热过程进行了三维数值模拟，研究表明通道的主相和次相内的再循环流动增加了传热速率，同时分析了液滴长度、流道截面长径比对换热的影响。李婷等[6]同样也使用计算流体力学的方法对微通道内液-液Taylor 流的传热特性进行了研究，考察了壁面剪切力、界面涡度对传热的影响，发现Taylor 流动相较于单相流动和平行流更能满足高通量下的换热要求。

截至目前，有关弹状流（Taylor 流）对流换热特性的研究大多集中在气-液体系，液-液体系下的换热研究仍十分有限，尤其是对于高黏度油相的情况。本文采用实验方法对微小管内的液-液两相流动进行了流型可视化和换热研究。总结了通道内两相流型、液滴长度与形状等动力学特性。并在此基础上研究了低Reynolds数下弹状流与微小通道间的换热特性，分别考察了混合速度、含水率和液滴长度对传热系数的影响，可为微换热器设计优化提供一定的指导。

1 实验装置和方法

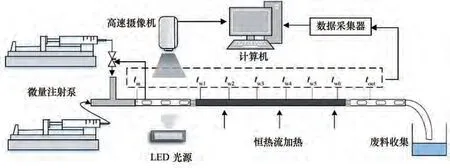
图1 实验装置图Fig.1 Schematic of the experimental apparatus

实验装置如图1 所示，两台高精度微量注射泵（TS-1B/ W0190- 1B, Longer, China, ±0.5%）用于两相供给并控制流速。使用了三个不同形式的接头，以在相同混合速度和含水率的条件下生成不同长度的液滴（droplet）和液弹（liquid slug）。加热管段选用内径(2 ± 0.04) mm，长400 mm 的铜管，其中加热长度为350 mm，外部包覆绝缘层。利用直流电源对铜管进行焦耳加热，以获得壁面恒热流边界条件。选用T型热电偶（0.2 mm头部直径）对管壁温度和流体温度进行瞬时监测。经恒温水浴校准后，所有热电偶的温度测量精度均在±0.2℃之内。热电偶与数据采集系统（安捷伦34970A）连接，对整个换热过程的温度变化进行监测。为了满足在传热实验运行的同时也能进行可视化观察，确定流动参数，在铜管前后分别设置了透明观察段。三部分管段的内径必须相同，这样可以保证流体经过连接处时不会因为直径不匹配而造成流动紊乱。流动可视化通过HX-6 型高速摄像机实现，拍摄速度设置为2000帧/秒。为了获得更好的可视化效果，透明管段下方放置了LED冷光射灯。

两相非混液体分别为去离子水和二甲基硅油，物性参数见表1（25℃，大气压）。

表1 工质物性参数Table 1 Physical parameters

为了确保计算精度，直接测量了所有工作流体的物理性质。密度通过测量已知体积液体质量加权得到，相对测量误差为± 2%。黏度测量采用Brookfield DV-II+Pro黏度计，相对测量误差为±1.0%，重复性为±0.2%。由于油相黏度随温度变化较大，这里测量了温度在20～60℃间油相所有黏度，在后面计算中根据测量的流体平均温度选择相应的黏度值。比热容通过差式扫描量热仪DSC25（TA Instruments,USA）测量，温度精确度± 0.01℃。每个液体取样三次并测量，测量结果标准偏差均小于8%。采用瑞典Hot Disk公司研发的TPS-2500s型热常数分析仪测量液体热导率。该仪器基于瞬变平面热源技术（TPS），能在很短的时间内完成热参数测量，并保证测量精度在±2%范围内。

2 实验结果与讨论

2.1 流型图分布

液-液流动的应用背景与其流型特征密切相关。在实际应用中，既可以根据不同需求选择不同的流型，也可以在特定的流型内根据需求来进行速率调控，进而增加操作弹性。例如滴状流可以用于微粒子加工[21]，而化学反应、萃取和混合等强化传热传质过程一般发生在环状流和弹状流下[22-23]。因此流型分布的准确预测在工程应用中有着重要的意义。

2.1.1 液-液两相流型本实验中所使用的石英玻璃通道壁面疏水，当两相流体在通道中流动达到稳定状态时，水相始终作为分散相存在，而油相为连续相。为了尽可能减小初始状态下壁面润湿状态对液滴形成过程的影响，实验开始前令通道内充满油，随后引入水相。待两相流动稳定后，再对特征流型进行捕捉。通过改变两相表观流速观察到以下五种特征流型：滴状流、弹状流、联结弹状流、环状流和分层流，见图2。

图2 液-液两相体系内流型Fig.2 Liquid-liquid two-phase flow pattern

图2(c)、(d)为两相流中最典型的流型：弹状流（slug/Taylor flow）。这种流型因其独特的内循环结构而大大提高了流体径向运输的能力，因此在化学分析和热管理系统中有着重要的应用。不同流量比下，弹状流中液滴长度会有所不同，但其基本流型特征并不会改变：分散相液滴几乎充满通道；液滴长度通常大于通道直径；分散相液滴（droplet）和连续相液弹（liquid slug）交替分布；液滴与壁面间会存在一层薄薄的液膜。如图2(a)所示，滴状流流型基本特征和弹状流相似，但液滴尺寸小于通道直径。由于连续相流速较大，液滴生成稳定性也往往较差。随着两相流速的增加，流型的规律性大大降低，出现以下三种主要流型：联结弹状流、环状流和层状流。联结弹状流[图2(b)]是弹状流和环状流之间的一种过渡流型，两相界面呈周期性波纹状，波纹大小随混合速度变化而变化。当流型为环状流时[图2(e)]，两相界面逐渐趋于平缓，分散相和壁面之间存在一层均匀液膜。分层流发生在两相流速都很大的情况，两相界面也是波纹状的，但并不规则。

2.1.2 流型转换图不同流型的出现是由各种作用力相互竞争作用所导致。由于通道尺寸大大减小，重力影响是可以忽略的（Bo ≪1，Bo=gd2(ρl-ρg)/(4σ)）。而宏观尺度下往往忽视的流体界面张力、黏性力等开始占据主导地位。在此过程中，界面张力通过减小两相接触面积来使界面能达到最小；惯性力使得界面在流动方向上延伸，流体保持连续；黏滞力则会耗散界面上的摄动能量，使两相界面趋于光滑。针对实验得到的几种特征流型，绘制了流型转换图（图3）。选用表观速度（j）和毛细管数（Ca）为变量，来反映液-液两相体系中不同内部作用力的竞争关系对流型转换的影响。

本实验中，分散相和连续相毛细管数范围分别为3.98×10-5＜Cadp＜0.001275, 0.0046 ＜Cacp＜0.148。对于滴状流和弹状流等规律流型，界面张力相对于黏性力和惯性力始终占据主导地位以能够维持特定的液滴形状，因此它们的流型均分布在毛细管数相对较小的区域（Cadp＜0.001, Cacp＜0.12）。其中弹状流所处范围较广，两种液体表观速度大小相当。滴状流则发生在高连续相速度和低分散相速度的情况下（大油水比下），由于连续相的高动量，使得分散相很容易断裂生成小液滴并向下游流去。随连续相流速继续增加，惯性力作用增强，流型会出现液滴大小间隔不均等不稳定现象。当惯性力主导流动时通道内的主流部分是连续的，这与环状流流型特征是吻合的（Cadp＞0.001,Cacp＜0.02)。这时jdp＞＞jcp,连续相黏滞作用基本可以忽略，水相几乎充满通道形成环形内核，连续相包覆在分散相周围形成液膜。随着油水比增加，惯性力作用减小，界面张力开始在一定程度上控制流型，内核流动虽还是连续的，但在油水界面出现了波纹形状，此时流型为联结弹状流[图2(b)]。如果界面张力作用继续增加，这种波动就会越来越明显，甚至使内核流动发生断裂，形成长液滴。相反，如果惯性力继续增加，则联结弹状流会向分层流过渡。所以联结弹状流是发生在弹状流向环状流或分层流过渡时的一种中间态流型，分散相液滴虽不是孤立的，但两相界面仍会维持一定的周期形状。分层流是发生在两相流速都很大的情况（jdp＞0.035 m/s, jcp＞0.035 m/s），此时两相惯性力作用都很大，各自分层流动。但同时也能注意到，通道壁面上附着的油性黏膜一直限制着水的流动，随着流动向下游进行，惯性力逐渐耗散，界面张力作用凸显，导致分层流的后半部分波纹更加明显。

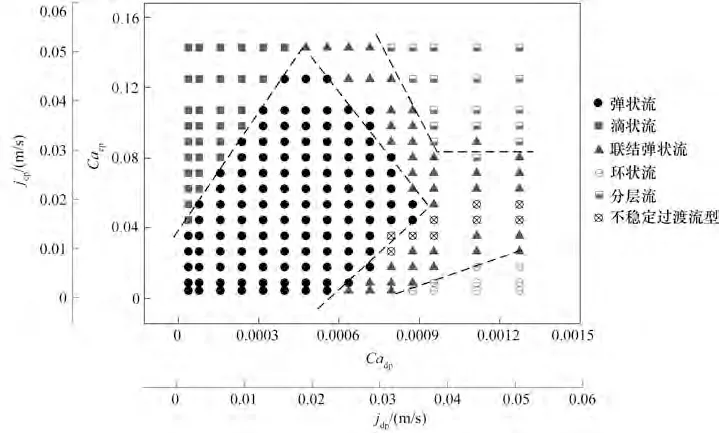
图3 水-硅油体系内两相流型转换图Fig.3 Flow pattern transition map in water-silicone oil system

2.2 弹状流特征长度及形状

很多因素都会在一定程度上影响液滴长度，如通道壁面接触角、两相流量比和毛细管数等[24-25]。但通常来说液滴长度是由通道尺寸大小直接决定的。无论是对于气-液两相流还是液-液两相流，单相流速改变对气泡/液滴长度的影响是一致的，均随着同相速度的增加而增加，随着另一相速度的减小而减小[26]，因此在这里不再做过多的讨论。选取混合速度为变量，分别对五组油水流量比下的液滴长度、液弹长度和Taylor单元长度进行了考察，结果见图4 和图5。实验中所有特征长度都是通过测量预设标尺长度的像素点数量，再测量液滴两端像素点数量，对比计算得到的。相同工况下的特征长度共取五组分别进行测量，再取平均值作为计算用值。图4(b)是基于图4(a)中所圈选工况下的液滴形状，为了更好地对液滴边界进行观察，将其进行了二值化处理。

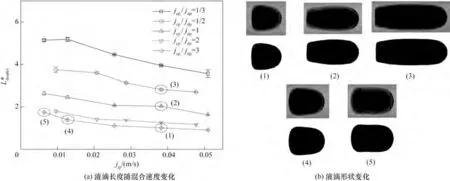
图4 混合速度及两相流量比变化对液滴长度和形状的影响Fig.4 Effect of mixing velocity and flow rate ratio on the droplet length and shape

图5 液弹和Taylor单元长度随混合速度变化趋势Fig.5 Effect of mixing velocity on the length of liquid slug and Taylor unit

表2 液-液两相体系中液滴长度预测公式Table 2 Empirical correlation for droplet length in liquid-liquid two-phase systems

图4(b)展示了高速摄像捕捉到的液滴原始图像以及二值化处理后的液滴轮廓。液滴编号见图4(a)，分别设置在特定油水比（jcp/ jdp= 3）和混和速度（jtp= 0.0382 m/s）下。和Taylor 气泡相似，液滴也有着较尖的头部和相对平直的尾部。随着油水比减小，液滴逐渐变长，但其头部和尾部半月面形状基本保持不变。而在固定的油水比下，随着混合速度的增加，头部半月面曲率逐渐变大，液滴尾部逐渐趋于平直。这一发现在他人研究中也得到验证。如Chen 等[31]报道了混合Reynolds 数对孤立Taylor 气泡前后形状的影响，认为在低Re时，Taylor气泡的前后两侧都呈现出半球形的帽状，随着Re 的增大，气泡头部曲率半径变小，而尾部逐渐变平。Taha 等[32]发现在低Ca 时，气泡两端曲率几乎相同，随着Ca增加Taylor 气泡头部变尖，且气泡周围的液膜会增厚。Gupta 等[33]通过实验和数值模拟方法对Taylor液滴进行了研究，发现液滴前后半月面的形状与液滴体积大小无关。随着混合速度的增加，液滴头部半月面曲率半径减小，但液滴尾部的曲率却始终不变。

2.3 弹状流下换热

2.3.1 对流换热验证与计算整个换热系统的热平衡可以用式（1）表示：

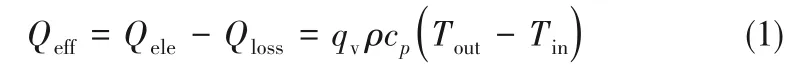
式中，qv、ρ、cp、Tout和Tin分别为体积流量、流体密度、流体比热容、出口流体温度和入口流体温度，Qeff为流体吸收有效热量，Qele为电加热总热量，Qloss为系统对环境的热量损失。

能量损耗率η可以表示为：

考虑到加热管道壁厚较薄，铜的热阻较小。实验中只检测了外壁温度Tw,out，内壁温度Tw,in则通过一维导热方程计算得到：

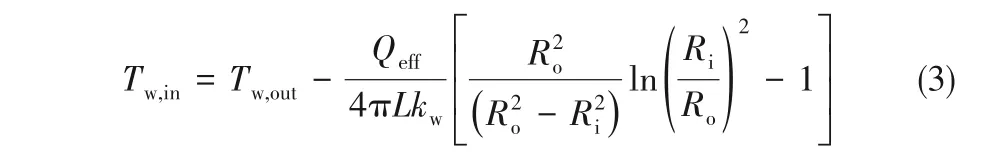
式中，Ri和Ro分别是内、外管半径；kw是铜管的热导率，经计算所有工况下的内外壁温差都很小，均小于0.1℃。

图6 换热装置验证Fig.6 Verification of experimental heat device

为了验证实验的正确性，在无流体流动和单相水层流条件下对加热系统进行了换热分析，结果见图6。其中壁面温度为25～60℃，单相水层流流动Re 为50～126.8。由图6(a)可以看出在加热空管时，外管壁六个测温点均呈线性增加。起初温度相差很小，随着温度升高，各测温点温度偏差稍有增大。但误差都在4.6%之内。基本可以认为加热区域通过管壁传递的热量是均匀的。由于实验设置了良好的绝热层，热耗散较小。从图6(b)中可以看出热耗散率η 基本维持在20%左右，表明电加热的大部分能量是转移到流体中的。综上可以认为实验换热系统是合理的，监测到的温度数据是可信的。

对于多组分液体流动，流体的热力学性质是由各组分液体之间的热平衡来定义的。液-液体系中，当分散相液滴和连续相达到热平衡时，可以采用均质流模型来进行流体物性的计算[34]。这也是在两相流换热实验研究中常用的物性计算方法[14,35]。将两相流动视为具有单一平均流体性质的单相流体，平均流体性质取决于混合物中各相质量分数。这时，式（1）变为式（4）：

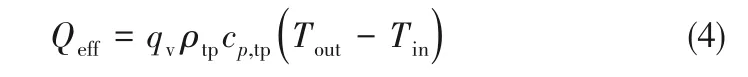
式中，ρtp为两相混合密度，cp,tp为两相混合比热容，均通过两相质量加权平均计算得到。

式中,φ为分散相质量分数。

2.3.2 两相混合速度和含水率对换热影响弹状流下不同的流体动力学参数会影响换热能力，这些参数主要包括：含水率、液滴长度、混合速度、液膜厚度、壁面接触角大小等。充分理解这些参数对换热的影响对于设计基于液-液两相流的微换热装置有着重要的参考作用。

图7(a)为固定两相流量比下平均Nusselt 数（Nutp）随混合Reynolds数Retp的变化曲线。

图7 Retp和含水率对传热系数的影响Fig.7 Effect of Retp and water content on heat transfer coefficient

平均Nusselt数Nutp定义为

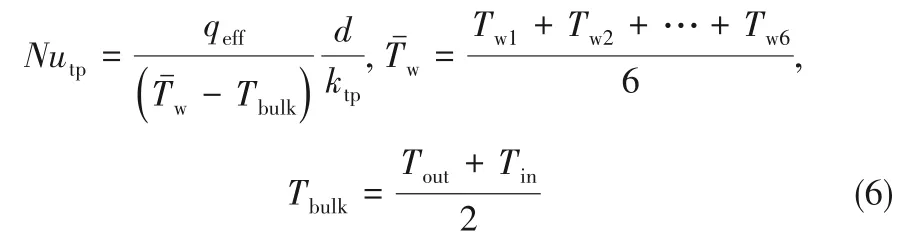
需要注意的是，由于计算采用均相流模型，在固定流量比下混合密度和混合黏度都是常数，因此Nu 随Retp的变化趋势也就是Nu 随jtp的变化趋势。可以看出在油水比相同的情况下，平均Nusselt 数随着Reynolds 数的增加而增加，且油水比越大传热系数增加幅度越明显。由图4 可以看出，对于高黏度低Re 下的弹状流，液滴/液弹长度随着混合速度的增加而变短。短的液滴/液弹缩短了其内部循环所需时间，进而强化了整体换热。其次，混合速度的增加会使两相冷流体运动加快，这就使壁面与冷流体间始终保持较大的温差，也会在一定程度上增加传热系数。但这种效应在低Re下似乎是不明显的，如Dai 等[14]同样在较低的Reynolds 数范围（15 ＜Re ＜48）研究了液-液两相流换热特性，发现混合速度几乎是不影响传热系数的。这主要是因为他们所使用的连续相黏度较小（Ca ＜0.0043），液滴长度与混合速度彼此独立导致的。相对Nusselt 数Nu*（Nu*=Nutp/Nusp）随含水率β的增加呈下降趋势，见图7(b)。这是因为随着油水比增加，液滴长度变短，液滴内部内循环强度增加。在含水率变化范围内0.17 ＜β ＜0.83，Nu*几乎均大于1，表示弹状流下传热系数始终高于单相水层流流动的情况，对换热是起到强化作用的。虽然随着系统内含水量β增加会使两相平均热容量提高，但这种提高被其长液滴内较弱的循环强度所抵消，这种现象尤其在低Re 下更为明显，液滴内部流体需要很长的时间才能循环一个周期。可以发现内循环效应是弹状流中强化换热的主要机制。

2.3.3 液滴长度对换热影响由以上分析可以看出，许多流动参数的改变都会影响液滴长度，进而影响换热。为了将液滴长度这一变量独立开来，选用三种不同形式的接头（T 型接头、Y 型接头和十字型接头），在相同混合速度和油水比的情况下生成不同长度的液滴/液弹。

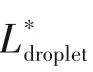
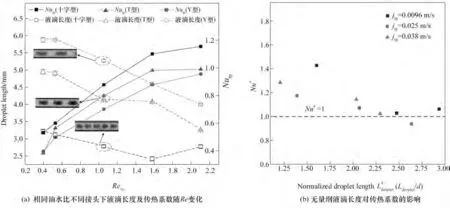
图8 液滴长度对换热的影响（jcp/jdp=1）Fig.8 The effect of droplet length on heat transfer coefficient

总地来看，当前实验条件下液-液弹状流较单相水层流换热有所增强，最高为80%。但相比其他研究，强化换热效果相差很多。如Abdollahi等[15]和Egan 等[19]在液-液Taylor 流下的传热研究，传热系数较单相分别提高了700%和600%。此外，该实验工况下无论是单相流还是弹状流的Nu都在1～2 范围内，均低于恒热流条件下管内层流充分发展换热的Nu 理论值4.36。这些现象的主要原因均是由当前实验下连续相的高黏度（大毛细管数）所引起的。低Re 下流体内部存在轴向热传导，Nu 较低，这在以往的研究中也有发现[37]，说明尺度效应在低流量流动中起关键作用。同时，由于连续相流体黏度高，流动Re 低，贴近壁面处的层流底层（油相液膜）热导阻力与对流阻力也是不能忽视的。所以在考虑两相换热时应该尽可能让高热导率流体作为连续相，可以通过壁面设置亲水来实现。

3 结论

基于实验研究的方法对微小圆管内的液-液两相流开展了流体动力学和换热特性研究，主要结论如下。

（1）流速供给范围内观察到五种特征流型：滴状流、弹状流、联结弹状流、环状流和分层流。其中滴状流和弹状流发生在界面张力主导区域。当惯性力主导流动时通道内的主流部分是连续的，环状流发生。分层流发生在两相流速都很大的情况（jdp＞0.035 m/s, jcp＞0.035 m/s），两相惯性力作用都很大，各自分层流动。

（2）与气-液Taylor 流和低黏度液-液弹状流不同，高黏度连续相下，随着两相混合速度增加，液滴长度和Taylor 单元长度均会减小。随着油水比减小，液滴逐渐变长，但其头部和尾部半月面形状基本保持不变。而在固定的油水比下，随着混合速度的增加，头部半月面曲率逐渐变大，液滴尾部逐渐趋于平直。

（3）平均Nusselt 数随着Reynolds 数的增加而增加，且油水比越大传热系数增加幅度越明显。Nu随含水率的增加而降低。在含水率变化范围内0.17 ＜β ＜0.83，随着含水率增加，虽然两相平均热容量提高，但在低Re 下，这种提高被其长液滴内较弱的循环强度所抵消。

（4）短的液滴/液弹缩短了其内部流体循环所需时间，进而强化了换热。实验结果表明，相同条件下，液滴长度的优化使整体传热系数提高了近26%。

符号说明

Bo——Bond数

Ca——毛细管数

d——直径，m

j——表观速度，m/s

kw——加热管壁热导率，W/(m·K)

L——长度，m

Nu——Nusselt数

Nu*——两相流相对于单相水层流下的Nusselt数