基于PANDA 平台的飞行器脉动压力激励随机振动响应分析

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

飞行器在再入大气层时，外表面的流场将诱导复杂的脉动压力作用，脉动压力是飞行器产生随机振动的主要载荷源。脉动压力可以通过风洞试验、飞行试验或流体分析计算等获取。得到脉动压力分布后的结构动力学计算仍具有一定难度：首先再入飞行器处于自由飞行状态，自由状态下的动力学分析面临刚度矩阵奇异问题；其次，再入飞行器不同部位所承受的脉动压力各不相同，属于多点相关激励问题。以脉动压力为载荷条件，建立面载荷、自由体结构振动响应数值模拟预测技术，对形成较为全面的再入飞行力热环境预测能力有重要意义。

在航空航天领域，众多的商业软件被用来进行结构力学分析，但使用商业软件面临着分析自由度受限等问题。目前国内正在积极开发拥有自主知识产权的高性能力学分析软件，比如 PANDA[1]、PHG[2]、PFEPG[3]等。其中 PANDA（Platform for Parallel Adaptive Nonlinear Dynamic-and-static Analysis）是中国工程物理研究院研发的大规模有限元并行分析软件平台，具备千万自由度、上千CPU 核应用程序开发所需的并行支撑环境能力。在PANDA 平台过往的研究中，对随机振动分析功能的研究主要集中于约束结构和受基础激励的情况[4-7]。

文中针对自由结构受脉动压力激励的情况，介绍相关的理论，并基于PANDA 平台进行软件实现。利用自研软件对自由状态的飞行器结构受到多个实测脉动压力激励的情况进行分析，与某商业有限元软件对比结果，对PANDA 平台针对自由体的脉动压力激励的随机振动响应分析功能进行测试和验证。

1 自由体脉动压力随机振动相关理论

1.1 自由体模态分析

对于自由体结构，模态分析形成的总体矩阵存在奇异性，影响计算结果。为消除刚度矩阵的奇异性，可以采用谱变换技术进行处理，模态分析对应的广义特征值问题为：

式中：x为广义特征向量；λ为特征值。对刚度矩阵K进行移位变换，式(1)可以变换为：

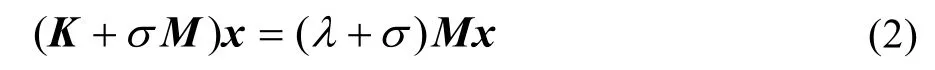
式中：σ为谱变换移位值。通过式(2)的谱变换，原来的刚度矩阵K变为K+σM，相当于在原来刚度矩阵基础上对各个自由度施加了1 个约束，通过选取合适的移位值消除刚度矩阵本身的奇异性，从而便于求解。对比式(2)和式(1)可以发现，谱变换后，方程的特征向量并未改变，特征值由原来的λ变成了σ+λ。在具体实现中，只需要将原来的刚度矩阵算子K替换为K+σM即可。求解后的模态振型保持不变，而模态频率在原来基础上统一减去σ，即为原来自由体所对应的模态频率。

1.2 随机振动分析

对于振动分析，离散后的运动方程可以表示为：

式中：C表示阻尼矩阵；u表示节点位移向量；f表示脉动压力的载荷离散向量。式(3)中的载荷向量f由脉动压力载荷离散而来，这涉及到面载荷到节点载荷的等效处理。压力载荷在单元上通过数值积分转化成等效的节点载荷，一般可以表示为：

功率谱密度与脉动压力之间的关系为：

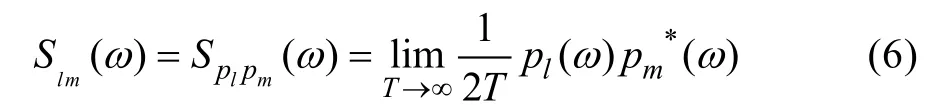
式(6)中，当l=m时，对应自谱，当l≠m时，对应互谱。采用模态叠加法进行解耦，将位移转换到模态坐标系下：

式中：φj为第j阶模态振型；ηj为模态坐标。对于第j个模态坐标，有：

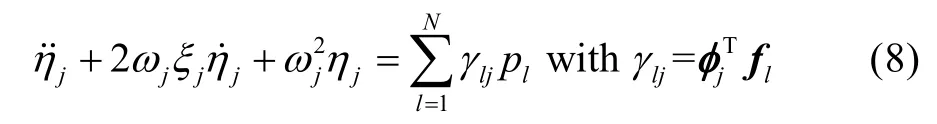
式中：γlj为模态参与系数，下标l和j分别对应压力激励和模态阶数。式(8)在频域内的解为：

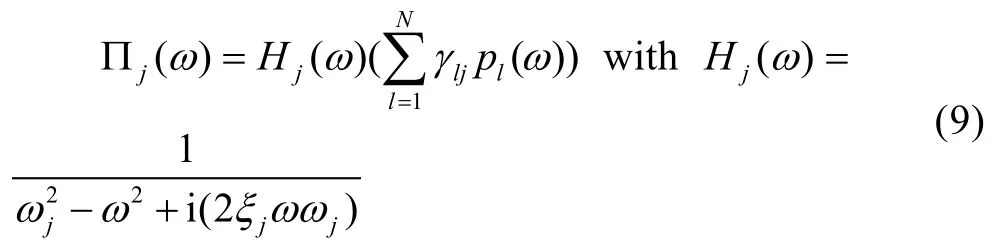
式中：Hj(ω)为频响函数。根据模态功率谱的定义，位移的自功率谱密度表达式为：

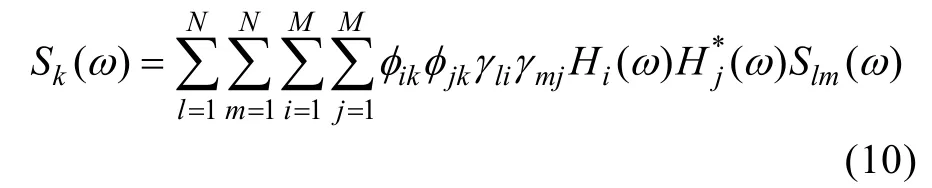
式中：k表示自由度。速度、加速度功率谱密度和位移功率谱密度之间的关系为：

第k个自由度对应的位移（或速度、加速度）均方根值可以表示为：

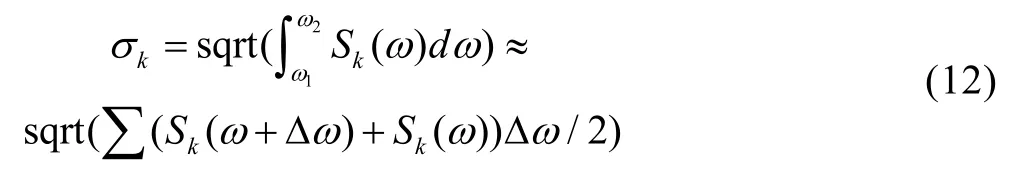
2 并行实现简介

PANDA 平台基于JAUMIN 框架[8-9]数据结构研发有限元分析平台，目前具有静力学、模态和振动、冲击动力学等多个并行分析软件，自由体脉动压力激励随机振动响应分析功能是其中的一个求解模块。PANDA 平台的架构如图1 所示。自由体脉动压力激励随机振动响应分析由多个基本功能组合形成，如图2 所示。

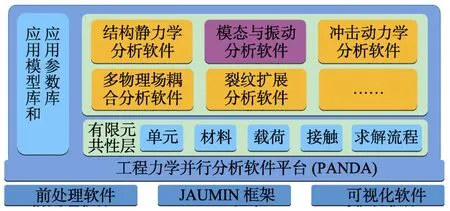
图1 PANDA 平台结构Fig.1 The configuration of PANDA platform

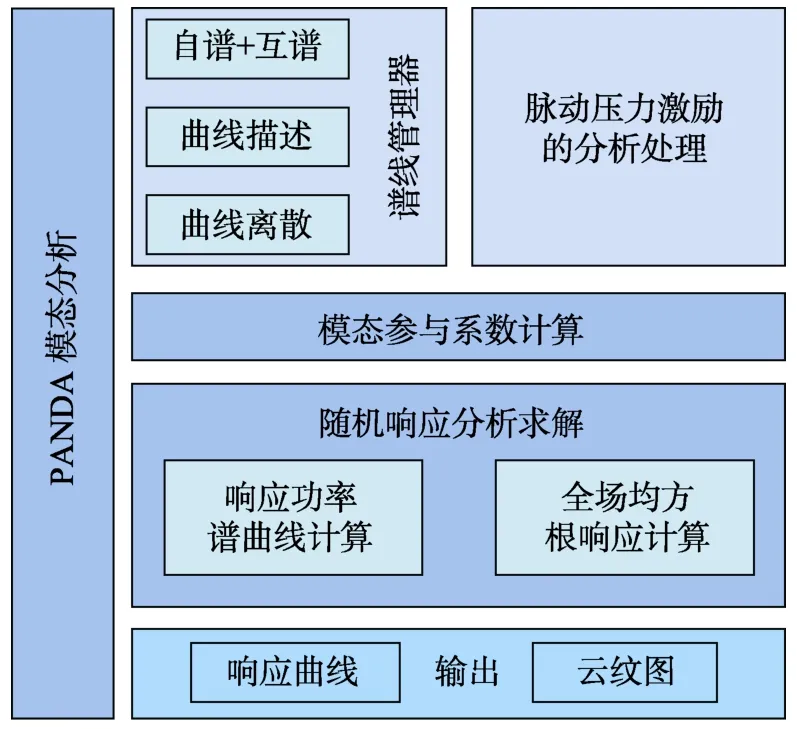
图2 随机振动响应分析基本功能组合Fig.2 The basic computing flow of random response analysis

从图2 中可以看到，模态分析是响应分析的基础，该阶段给出结构的模态振型和固有频率。谱线管理器解析输入激励，包括自功率谱密度曲线（实数）和互功率谱密度曲线（复数）。对于每个脉动压力激励，都会计算对应的等效节点载荷向量，并利用其与模态振型来计算模态参与系数。指定节点自由度自功率谱密度和计算全场的均方根响应的计算，需要用到模态参与系数、频响函数、各阶模态振型以及输入的功率谱密度。计算结果以响应曲线和云纹图的形式输出。

以上过程中的并行基于单元和自由度展开，在结构的单元计算和矩阵组装、总体方程组求解、模态参与系数计算、全场均方根响应计算等阶段有很好的体现。其中总体特征值方程组的求解依靠集成的Krylov-Schur 算法和Jacobi-Davidson 算法[10-11]完成。

以下针对飞行器算例，开展多点脉动压力载荷作用下的功率谱密度响应以及均方根响应计算和对比，对研发模块的正确性进行验证和展示。

3 飞行器响应分析

3.1 模型介绍

飞行器离散后的有限元模型如图3 所示，飞行器处于自由状态，不施加任何约束。PANDA 和商业软件中都采用六面体实体单元进行网格划分，网格单元保持一致。选取其底部某点为关注点，用五角星表示。结构承受脉动压力的分布情况，从飞行器前段开始，将脉动压力分成3 段，每段分为上部和下部，共计6个不同的区域，如图4 所示。

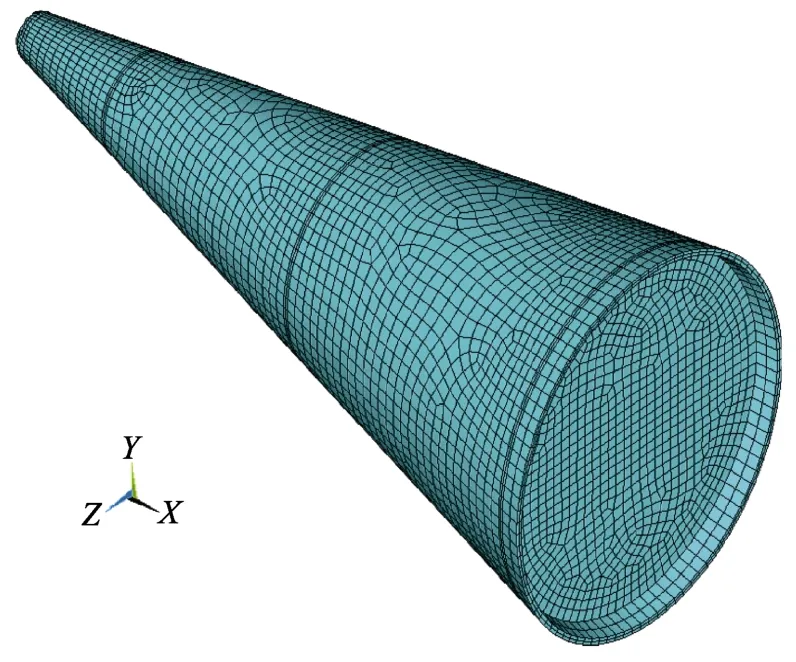
图3 飞行器有限元模型和关注点Fig.3 FE model of aircraft ant the foucs point

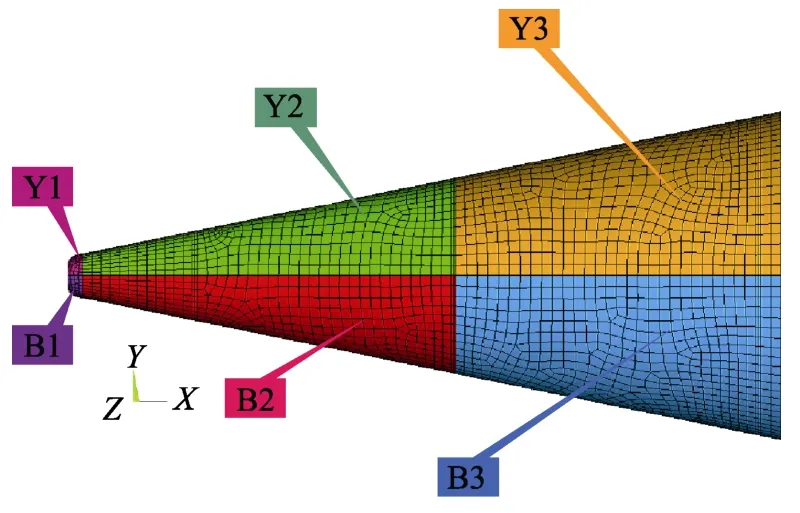
图4 飞行器所受脉动压Fig.4 The pressure on the aircraft

飞行器表面6 个不同区域受到的脉动压力功率谱密度（PSD）曲线如图5 所示。

3.2 模态分析

计算结构前2000 Hz 的固有频率，PANDA 和商业软件的对比结果如图6 所示。从图6 中可以看到，2000 Hz 内共有89 阶模态，PANDA 与商业软件的结果都吻合得很好。前6 阶是刚体模态，固有频率为0，脉动压力随机振动分析只采用从第7 阶开始的弹性模态。

图5 不同区域激励曲线Fig.5 The PSD on area of different regions

PANDA 与商业软件计算得到的模态振型也是一致的，这里列出前5 阶弹性模态振型的对比情况，如图7—11 所示。

从图7—11 中可以看到，PANDA 与商业软件给出的前5 阶弹性模态在云纹分布上是一致的，各阶模态的最大值的差异也小于0.2%。这说明了PANDA 平台模态频率分析功能的正确性。

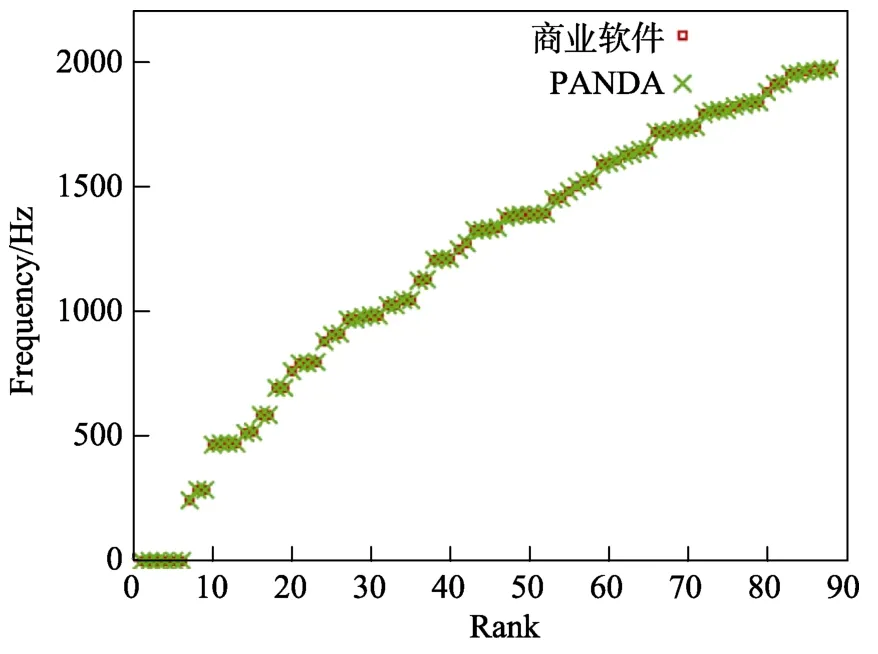
图6 模态频率对比Fig.6 Modal frequency comparison

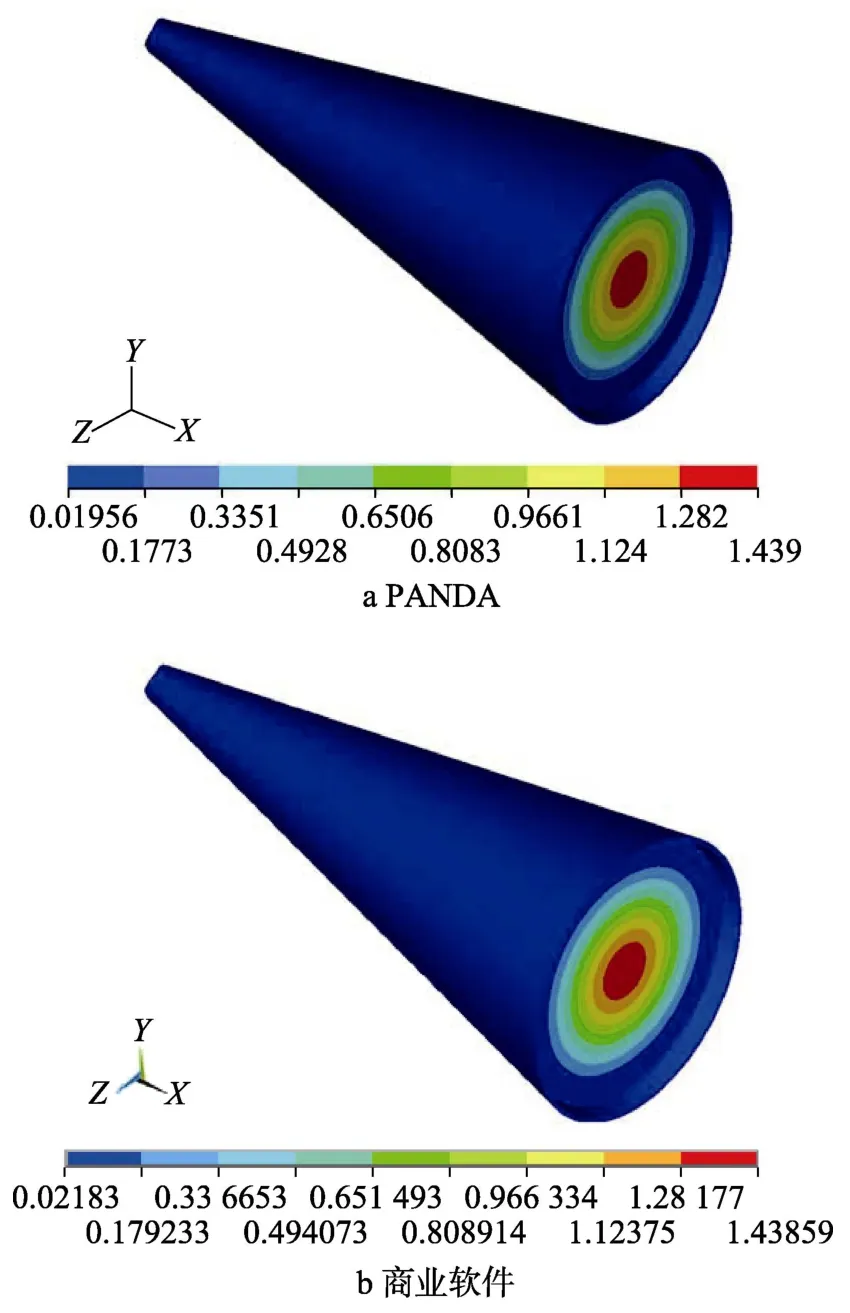
图7 结构第7 阶模态振型Fig.7 The seventh order mode deform contour of six DOFs platform:a) PANDA;b) business software

3.3 响应分析

在6 个区域不同脉动压力激励的作用下，计算结构的位移响应。取结构前2000 Hz 内的弹性模态进行叠加，各阶模态的阻尼比设为常值0.015。分析关注点3 个空间方向的位移响应功率谱密度曲线，并与商业软件结果进行比较，如图12 所示。

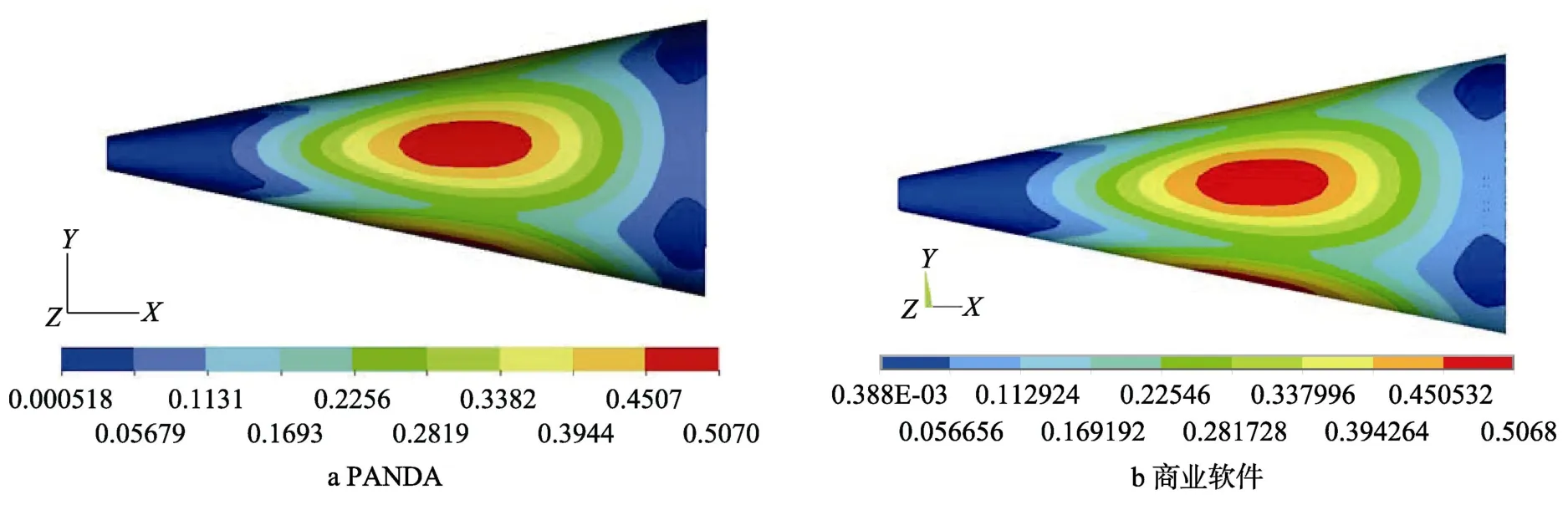
图8 结构第8 阶模态振型Fig.8 The eighth order mode deform contour of six DOFs platfrom:a) PANDA;b) business software

图9 结构第9 阶模态振型Fig.9 The ninth order mode deform contour of six DOFs platfrom:a) PANDA;b) business software

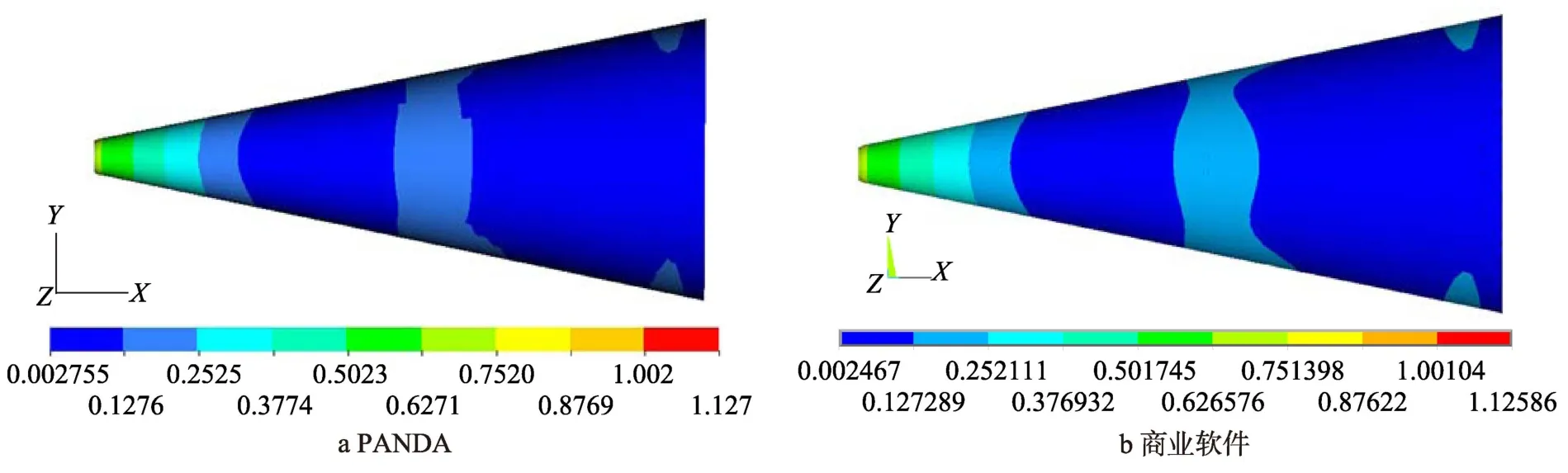
图10 结构第10 阶模态振型Fig.10 The tenth order mode deform contour of six DOFs platfrom:a) PANDA;b)business software

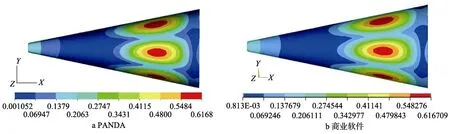
图11 结构第11 阶模态振型Fig.11 The eleventh order mode deform contour of six DOFs platfrom:a) PANDA;b) business software

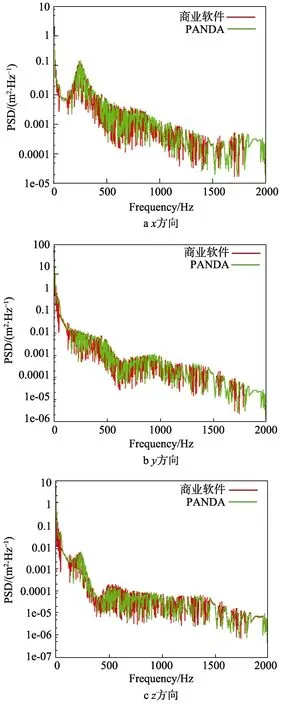
图12 关注点3 个空间方向上的位移响应对比Fig.12 Comparison of the displacement response in three spatial directions (a)x-scale,(b) y-scale,(c)y-scale

从图12 中可以看到，对于关注点的位移功率谱响应曲线，PANDA 平台和商业有限元软件的计算结果是基本一致的。由于频率离散方法的不同，计算结果中频率点的密度不一样，商业软件的结果中频率点更密集一些，特别是在小于50 Hz 的低频阶段。

PANDA 平台和商业软件计算的结构位移均方根响应对比如图13 所示。可以看出，在云纹分布上，PANDA 平台与商业软件的结果是完全一致的。PANDA 平台和商业软件给出的最大值和最小值的误差分别为1.93%和6.14%。这也说明了PANDA 平台自由体脉动压力激励随机振动响应分析功能的正确性。

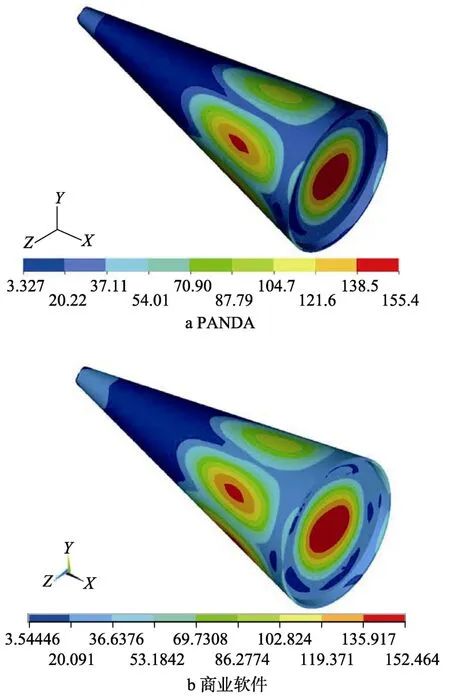
图13 位移响应云图对比Fig.13 Cloud image comparison of displacement response:a)PANDA;b) business software

4 结论

简要介绍了PANDA 平台脉动压力激励随机振动响应分析相关的理论公式和平台实现。针对无约束的简化飞行器模型，在PANDA 平台实现了结构模态分析以及脉动压力作用下的随机振动响应分析，开展了与商业软件的对比测试。结果表明：

1）在模态分析中，前2000 Hz 的模态频率分析结果，PANDA 与商业软件的结果完全一致。前5 阶弹性模态的模态振型云纹分布结果也一致，振型最大值的差别小于0.2%。

2）在脉动压力随机振动分析中，关注点在 3个空间方向上的位移响应曲线，PANDA 与商业软件的结果基本一致；结构的位移均方根响应云纹分布一致，最大值和最小值的误差分别为1.93%和6.14%。

通过对简化飞行器结构开展的对比测试，验证了PANDA 平台相关功能的正确性，并证明其对实际工程结构的可用性。