再入飞行器振动环境工程预示方法
2021-04-08
(中国工程物理研究院总体工程研究所,四川 绵阳 621999)
再入飞行器在飞行过程中所经历的动力学环境是非常复杂的,气流与结构之间的相互作用会导致其表面气流出现复杂的流动形式,包括湍流、分离流和激波振荡等[1-4],从而使得飞行器遭受严酷的脉动压力载荷,这种脉动压力亦被称为“气动噪声”[5]。脉动压力,作为再入飞行器飞行过程中所承受的随机激励,通过飞行器表面及其内部结构进行传递,会诱导飞行器结构产生剧烈的随机振动,将有可能导致飞行器结构的振动疲劳,甚至破坏。近年来,随着测量技术的不断发展,测量获得了一些飞行数据,为挖掘分析脉动压力与攻角、脉动压力与飞行振动的关联关系提供了数据基础。而再入飞行器飞行过程中,脉动压力诱发的随机振动环境载荷是确定力学环境设计要求及地面环境试验条件的主要依据之一。因此,通过对已有的飞行试验数据进行关联分析,研究预测脉动压力引起的再入飞行器结构振动环境载荷,对于再入飞行器载荷环境设计及保证飞行可靠性具有重要意义[6-8]。
国外对于飞行器在脉动压力载荷作用下的振动响应研究开始于20 世纪70 年代。Lakis 等人[9]研究获得了亚音速湍流脉动压力场作用下圆柱壳响应的理论解。随着计算机的飞速发展和有限元方法的成熟及推广,Elishakoff[10]采用有限元方法计算获得了壳体在随机激励下振型的耦合项对结构响应的影响规律,并逐步将相关研究成果用于环境预示工程。Mark S.Ewing[11]利用MSC.NASTRAN 软件分析了脉动压力载荷作用下飞行器简化梁模型的随机振动响应情况。该研究工作考虑了脉动压力载荷的相关性,并研究了载荷相关性对结构响应的影响。国内对飞行器脉动压力的随机振动响应研究起步较晚。20 世纪90 年代开始取得了一些进展,主要集中在运用有限元分析软件对随机振动响应的研究。徐孝诚[12]利用MSC.NASTRAN 软件计算了板壳组合结构在随机面分布力作用下的响应特征,并用实验结果校验了有限元计算结果,误差低于15%。该研究工作为利用有限元分析软件来分析飞行器气动噪声响应奠定了基础。随着飞行器技术的发展,气动噪声响应由单个面随机激励发展到多个面随机激励。尹立中等人[13]在文献[12]的基础上,探讨了有限元网格细化的标准,计算了某飞行器壳体在不同网格划分密度下的气动噪声响应,并采用实验结果对数值计算结果进行校验,在0~1000 Hz 范围内均方根加速度的相对误差控制在30%以内。杜骊刚[14]采用MSC.NASTRAN 对某飞行器自由-自由状态下的模态分析和气动噪声激励作用下的随机振动响应进行了计算分析,并与模态试验和噪声试验结果进行了对比分析,验证了有限元计算模型的有效性和正确性。在飞行器动力学环境载荷预示方面,目前主要采用的预示方法是继承相似型号或采用相关标准建议的试验条件、直接测量法、基于混合模型的宽频域数值分析以及基于实测数据的统计与外推技术。而国内外相关研究主要集中在理论模型、有限元等数值分析方法,缺乏在无法获得激励载荷和详细结构设计条件下的工程预示方法,无法满足再入飞行器结构和环境试验条件设计的快速迭代优化需求。
文中在飞行数据基础上,研究了振动环境载荷与脉动压力间的关联关系,构建了再入飞行器振动环境工程预示模型,为飞行器振动环境预示及精细化设计提供方法支撑,助力提高再入飞行器的研制速度和研究水平。
1 再入飞行振动环境诱因分析
再入飞行器飞行时,飞行器表面所受到的激励源是其表面气动流场诱导的脉动压力载荷,脉动压力通过拍打壳体引起壳体振动,再通过连接结构传递到飞行器内部,引起整个飞行器的振动响应。再入振动环境是一种非常复杂和严酷的环境,它与飞行姿态、马赫数、动压值、飞行器头部形状和表面状况等因素有关。由于再入动压和马赫数很大,再入段脉动压力引起的结构声致振动非常严酷。此外,不同飞行模式下,飞行器受到的激励源均是其表面的绕流流场诱导的脉动压力载荷,主要差异则体现在不同飞行模式其绕流流场特性的不同[15-16]。
飞行器外表面流场有很多不同的特性,例如湍流附面层、分离流、激波等,这些流场都会诱导脉动压力载荷。相比而言,分离流和激波流场比附面层湍流形成机理更复杂,产生的脉动压力更恶劣。流场特性诱导脉动压力载荷的主要机理有下列2 种(如图1 所示)。
1)当飞行器表面无突出结构或飞行零攻角等情况下,其表面流场一般为附面层湍流。此时产生的脉动压力量值一般与动压和马赫数有关,基本与动压成正比,与马赫数的平方成反比。
2)当飞行器在飞行过程中出现较大的攻角或表面具有突出结构时,其表面流场可能为分离流或激波流等,此时脉动压力量值除了与动压、马赫数有关外,还与攻角有关,变化规律更为复杂。
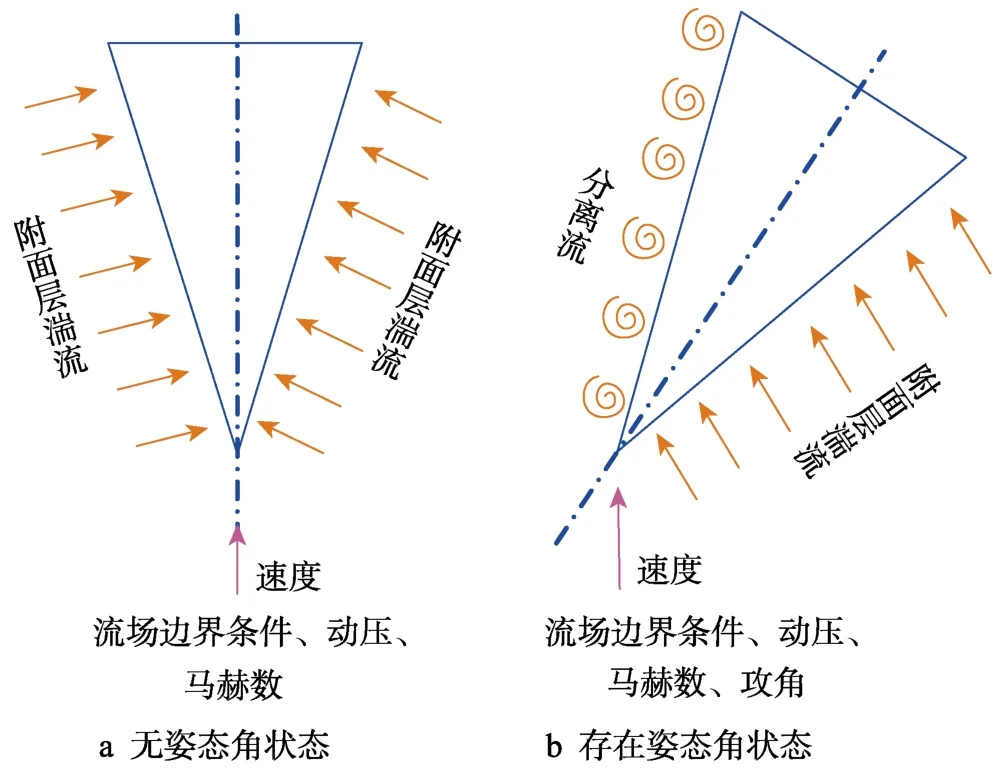
图1 再入飞行器激励源作用示意Fig.1 Schematic diagram of excitation source for re-entry vehicle:a) no attitude angle state;b) existing attitude angle state
2 考虑攻角因素的脉动压力预示方法
再入飞行器随机振动的主要激励源是脉动压力,因此振动环境外推预示需要解决的首要问题是对作用于飞行器的脉动压力进行预示。脉动压力的大小及变化规律取决于飞行动压、飞行器气动外形等因素。不同气动外形可以形成不同的附面层,如湍流附面层、分离流附面层和激波等,从而导致产生的脉动压力特征也会有所不同。
2.1 传统脉动压力预示方法
文献[1]对脉动压力环境的特性和预示方法进行了大量研究,主要是基于风洞试验。根据风洞试验数据,推导出了脉动压力与动压、马赫数的关系式,如式(1)所示。

式中:Cq为与动压和马赫数有关的系数,对于高马赫数流场,一般取0.01~0.03;q为动压,Pa;Ma为马赫数;Prms为均方根脉动压力,Pa。
根据以往型号经验,再入飞行段的振动比主动段更加严酷,而再入段振动响应的最大值通常出现在最大动压附近(如图2 所示)。因此只需对此时的均方根脉动压力及其功率谱密度进行准确预示,就可以确定再入飞行器的随机振动环境量级。
2.2 修正的脉动压力预示方法
在已有实测数据的基础上,对获得的再入飞行器振动环境与飞行姿态等数据进行统计分析,研究攻角与脉动压力之间的关系(如图3 所示)。从图3 可以看出,振动环境与横向过载变化规律基本保持一致。而横向过载的出现一般是由飞行器攻角引起的,较大的攻角会使飞行器表面气流分离,脉动压力量值将增大,从而导致飞行器振动响应增大。由此可知,再入飞行器的振动环境与动压、马赫数以及攻角是有关系的,飞行攻角的出现会产生严酷的振动环境。在实测数据分析基础上,辨识出脉动压力与动压、马赫数以及攻角之间的关系式,对脉动压力预示公式进行修正。
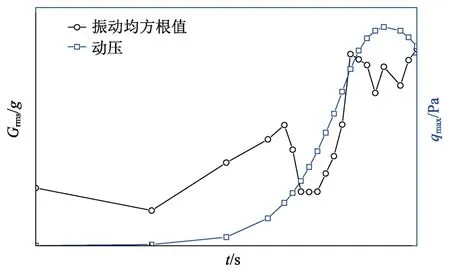
图2 再入振动均方根值及其相应动压变化情况Fig.2 Root-mean-square(RMS)value and corresponding dynamic pressure variation of re-entry vibration
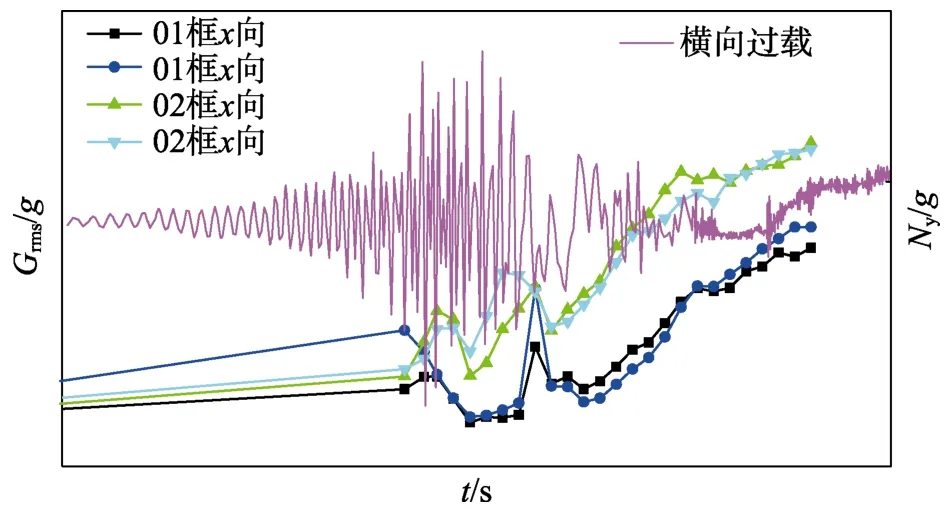
图3 再入振动均方根值和横向过载变化关系Fig.3 Change in the relationship between the RMS value of re-entry vibration and lateral acceleration
首先,通过历次飞行试验实测过载数据辨识出攻角或与攻角相关的“攻角系数”Calf,如式(2)所示。

式中:Calf为攻角系数;Ny为飞行试验实测横向过载,g;Nz为飞行试验实测径向过载,g;Nx为飞行试验实测轴向过载,g。
然后,通过数据分析识别,得到考虑攻角系数的脉动压力关系,如式(3)所示,攻角系数与脉动压力呈线性关系。同时,当Cq为0.016 时,各飞行器实测振动响应曲线与脉动压力变化曲线基本保持一致。

按式(3)计算了某飞行器再入飞行过程的脉动压力时间历程,并将脉动压力变化历程与振动均方根值变化历程进行对比,如图4 所示。从图4 可以看出,计算的脉动压力变化趋势与实测振动量值变化趋势基本一致,辨识出来的脉动压力与攻角、动压以及马赫数之间的关系式是基本合理的,可用于再入飞行器的脉动压力工程预示。
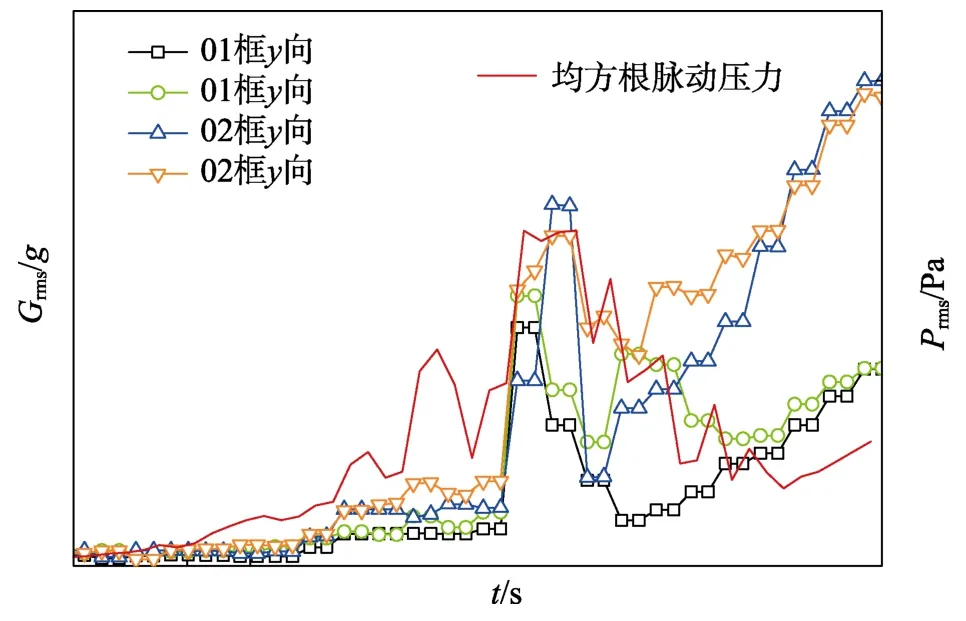
图4 再入飞行振动和均方根脉动压力时间历程Fig.4 Time history of re-entry flight vibration and fluctuating pressure of RMS
3 再入飞行振动环境预示方法
根据脉动压力与飞行振动环境关联关系的研究可知,第一峰值除了与动压和马赫数相关外,还与其他因素相关;而第二个峰值与脉动压力变化趋势保持一致。在设计初期,振动环境设计可按最大极值环境考虑,第二个峰值(落地前)往往是再入飞行器最大振动环境量值,而第一个峰值是由于飞行过程中边界层转捩导致的,但目前工程预测方法无法准确对转捩过程的振动特性进行预测。因此,该小节在研究基于实测数据的再入飞行振动环境预示方式时,不考虑转捩的影响。
在再入飞行器研制初期,一般利用外推方法来初步预示结构的振动响应量值,该方法在国内外被广泛采用[17-19]。根据相关文献研究情况,一般相似结构的振动响应与脉动压力功率谱密度呈正比,与质量面密度平方呈反比,外推关系式如式(4)所示[20],其中下标n 表示改型飞行器,下标r 表示原型飞行器。结构响应的预测精度取决于两个飞行器之间结构特性的相似程度。
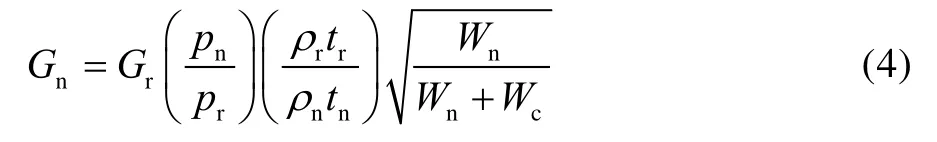
式中:G为振动响应总均方根加速度值;p为均方根脉动压力;ρ为面质量密度;t为舱壁厚度;Wn为结构质量;Wc为附加质量(即装在基本结构上的部件质量)。
假设相同飞行模式下脉动压力与再入飞行振动环境的关联关系是一样的,基于已获得的实测数据,挖掘分析获得均方根脉动压力和振动均方根值的关系,如图5 所示。
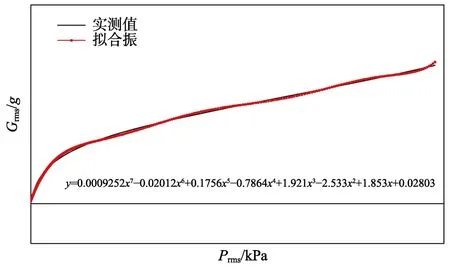
图5 飞行振动环境与均方根脉动压力关系Fig.5 Relationship between flight vibration environment and fluctuating pressure of RMS
在此基础上,结合均方根脉动压力与飞行振动关系,以及相似型号外推关系,获得的某飞行器再入振动环境与实测值对比情况,如图6 所示。从对比情况可知,预示的再入振动环境变化规律与实测情况基本吻合,在再入末期最大振动环境的预示误差约为40%。
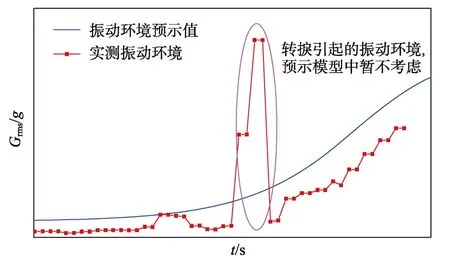
图6 某飞行器再入振动预测值与实测值对比Fig.6 Comparison between predicted and measured values of flight vibration for re-entry vehicle
4 结论
1)再入飞行器振动环境与动压、马赫数以及攻角是有关系的,飞行器飞行攻角的出现会产生严酷的振动环境。
2)通过实测数据综合分析,辨识出了脉动压力与动压、马赫数以及攻角的关系式,变化规律与型号实测情况基本吻合,修正的计算公式是正确的。
3)通过再入飞行气动参数与振动环境数据构建的基于数据驱动的振动环境工程预示公式是合理的。预示的再入振动变化规律与实测情况基本吻合,再入末期预示值与实测值偏差约为40%。
