考虑脉动压力相关性的自由体随机振动分析
2021-04-08
(中国工程物理研究院总体工程研究所,四川 绵阳 621900)
飞行器在再入飞行时受到复杂的载荷作用,外表面的高速绕流流场将诱导复杂的振动、噪声、过载和气动热等环境。在这些载荷综合作用下,再入飞行器以一定的加速度运动,处于没有约束的自由状态,整个再入飞行器为一自由体。在再入飞行器的结构响应分析过程中,通常从CFD 分析结果中提取再入飞行器的表面压力和脉动压力,作为结构分析的输入数据[1]。表面压力可以处理为静载,在准静态气动力作用下自由体作刚体运动。脉动压力则属于动态载荷,通过自由体结构及其内部气体和载体进行传递,会引起仪器结构及系统的振动响应,有可能产生复杂的环境效应,如结构破坏等可靠性和安全性问题。
脉动压力载荷的预示方法主要有经验公式法、数值模拟法和风洞试验[2-10],结构响应计算时,脉动压力载荷的处理方式可为单输入[11]和多输入[12-16]。脉动压力载荷是一种典型的随机载荷,一般采用随机振动方法和基于统计的能量法[17-18],统计能量法适合计算高频段的响应。低频段脉动压力下的结构响应可以通过面载荷自由体随机振动分析方法获得,自由体随机振动分析技术的难点是获得脉动压力的功率谱密度及各输入谱之间的相关性。目前为了简化计算方法,在施加多输入载荷时,忽略各个载荷之间的相关性,即假设计算对象外表面上各载荷输入点的随机载荷谱是完全相关或者完全不相关的[13-16,19-21]。在这种假设条件下得到的结构响应结果与真实情况存在差异。自由体在高速飞行中受到的脉动压力为面载荷,沿飞行器长度方向和环向非均匀分布,且不同位置的压力谱具有一定的相关性,对这种结构和载荷分布复杂的情况而言,完全按实际脉动压力加载存在一定的困难。文中通过对结构进行分区的方法,考虑各区域之间压力谱的相关性,利用有限元软件针对自由体结构在脉动压力载荷激励下的响应开展分析,研究自由体在脉动压力作用下的随机振动加速度响应规律,对于完善再入飞行器载荷设计和合理预测再入振动响应具有重要的工程应用价值。
1 自由体随机激振动响应计算方法
一个多自由度系统,当受到平稳随机过程X(t)的激励时,响应为Y(t),响应的相关矩阵为:

将式(1)中的Y(t) 和Y(t+)τ以卷积积分表示,用λ1和λ2作为积分变量,得:
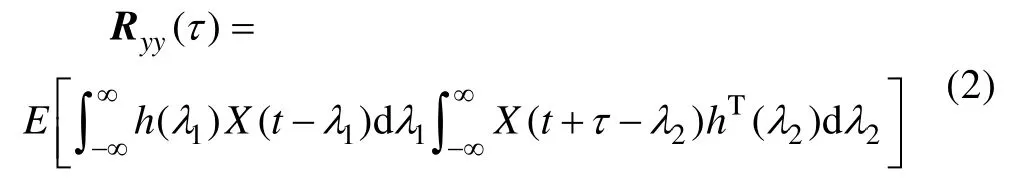
进一步处理后,可以得到响应与激励的相关矩阵之间的关系式:
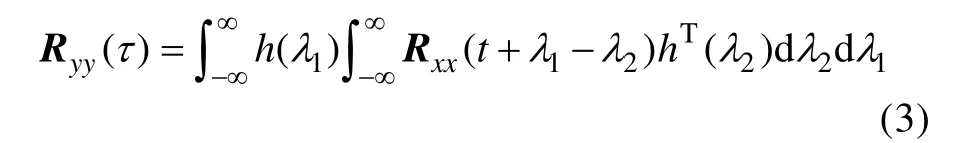
对式(3)进行傅里叶变换,得到响应与激励的功率谱密度矩阵之间的关系式:
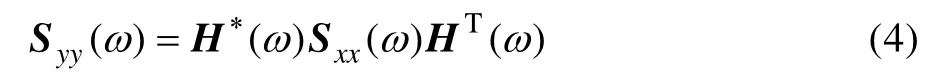
式中:H(ω)为频响函数矩阵,H*(ω)为H(ω)的共轭矩阵。
激励的功率谱密度函数矩阵Sxx(ω)为:
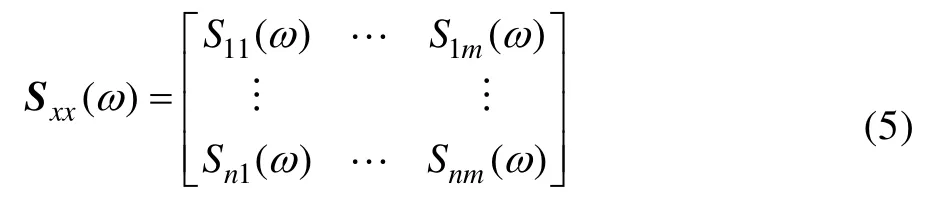
式中:当n=m时,Snm(ω)为自谱;当n≠m时,Snm(ω)为互谱。
相干函数为:

2 脉动压力的自谱与互谱
平稳随机过程脉动压力Xj(t)(j=1,m)的自相关函数为:
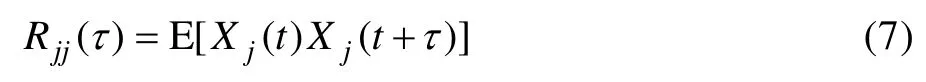
自谱为自相关函数的傅里叶变换,即:
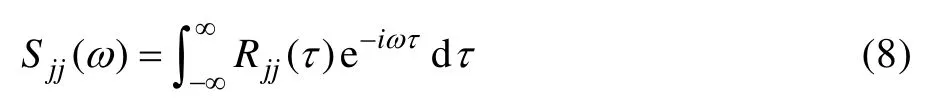
对于两个平稳随机过程脉动压力Xi(t)(i=1,m)、Xj(t)(j=1,m),其互相关函数为:

互谱为互自相关函数的傅里叶变换,即:

采用试验测试方法获得锥壳自由体结构不同位置的脉动压力时域曲线,通过编写程序对时域数据进行处理,根据上述公式获得脉动压力的自谱和互谱。
在锥壳自由体结构(如图1 所示)表面进行分区,沿长度方向分为3 个区域,沿环向分为4 个区域。在每个分区的中心位置布置压力传感器,通过试验获得测点的脉动压力时域曲线。限于篇幅,仅以测点1 和测点2 为例,其脉动压力时域曲线如图2 所示,通过程序处理后获得的自谱和互谱曲线如图3 所示。
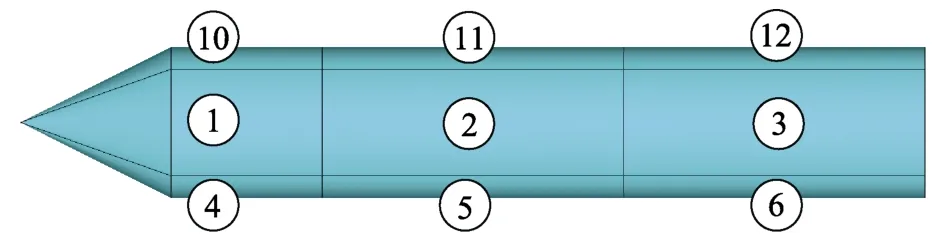
图1 表面区域划分Fig.1 Surface area division
3 锥壳自由状态计算结果
在自由体随机振动分析过程中,若考虑脉动压力载荷的相关性蒋导致载荷加载复杂,随机振动响应计算量随之增大。在传统的计算方法中都进行了相应的简化,为了获得压力谱之间的相关性对结构响应的影响规律,文中进行了如下3 种工况的计算:假设各个面载荷之间是两两不相关的,即;各个面载荷之间的相关性由实测时域载荷计算确定;假设各个面载荷之间是两两完全相关的,。
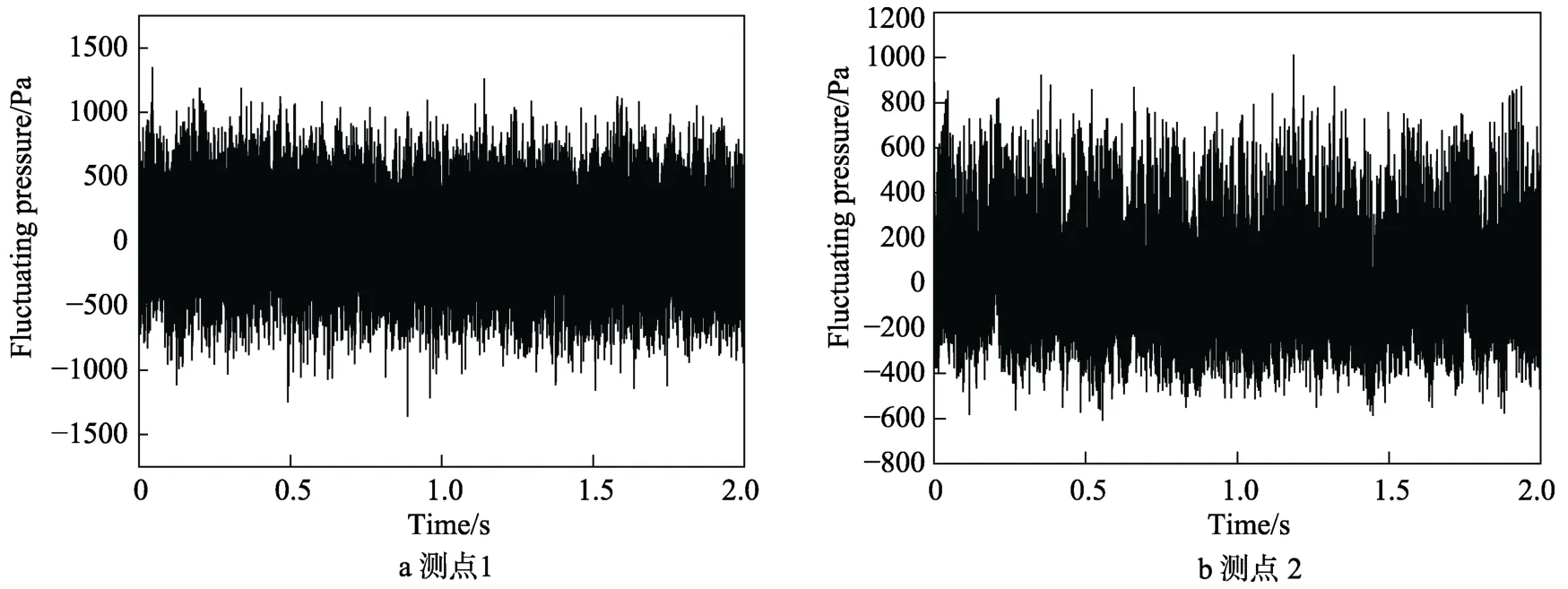
图2 脉动压力时域曲线Fig.2 Time history curve of fluctuating pressure:a) point 1,b) point 2
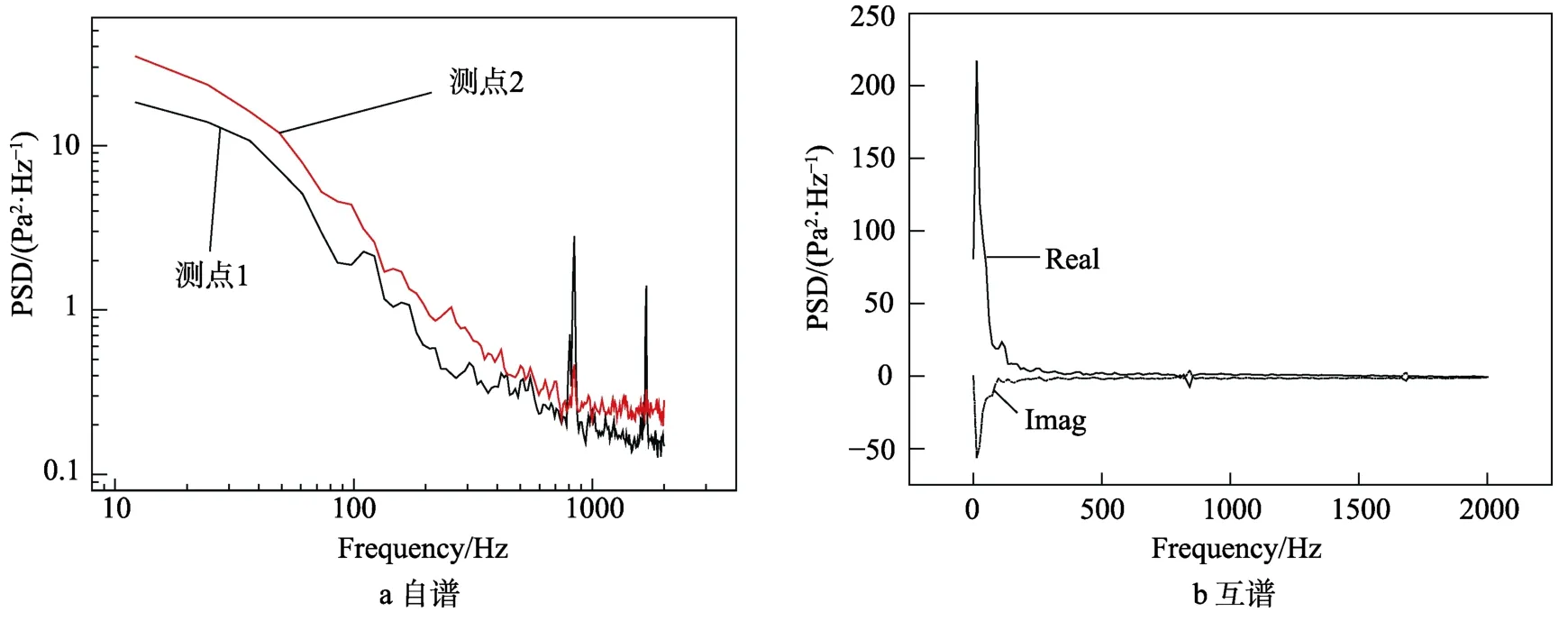
图3 脉动压力功率谱Fig.3 Power spectrum density of fluctuating pressure:a) auto spectra,b) cross spectra
采用有限元软件对锥壳自由体结构在脉动压力环境下的随机振动响应进行计算,有限元模型中的x、y方向如图4 所示,z向由右手法则确定。采用模态叠加法进行随机振动响应计算,整个结构为自由状态,阻尼比取2%,计算频率范围取0~2000 Hz。结构的有限元模型如图4 所示,a1,a2,a3分别为区域1、2、3 中心的节点。计算得到自由体锥壳表面加速度响应云图如图5 所示,3 个区域中心节点处加速度均方根值对比见表1。

图4 有限元模型及测点Fig.4 Finite element model and test point

图5 加速度响应分布Fig.5 Acceleration response distribution:a) no correlation;b)partial correlation;c) complete correlation

表1 加速度均方根值Tab.1 mean square value of acceleration g
从表1 的结果对比可以得出,各输入载荷完全相关的情况下计算得到的a1、a3测点加速度响应是偏大的,a2测点加速度响应是偏小的;各输入载荷不相关的情况下计算得到的a1、a3测点加速度响应是偏小的,a2测点加速度响应是偏大的,最小相差约15%,最大相差约50%。利用试验测得载荷进行空间相关性计算获得载荷之间的相关性,可以真实地模拟飞行器实际飞行中受到的脉动压力载荷,从而可以较准确地预测脉动压力环境下的结构随机振动响应。
4 结语
通过编写计算程序得到了自由体表面各测点之间脉动压力的互谱和自谱,并运用有限元软件开展了自由体在脉动压力面载荷环境下的随机振动响应分析,计算获得了自由体表面的加速度响应均方根值。通过不同相关性下的加速度响应计算结果比较,获得了载荷间的相关性对计算精度影响较大的结论。在频率域内探索出一条有效解决再入飞行器在脉动压力环境下结构随机振动响应问题的技术途径和方法,为今后开展再入飞行器脉动压力结构响应预示研究奠定了较好的基础。
