飞行器绕流流场脉动压力环境预示方法探讨

2021-04-08

装备环境工程 2021年3期

（中国工程物理研究院总体工程研究所，四川绵阳 621999）

导弹武器装备在贮存、运输以及飞行的全寿命剖面中，将受到各种环境的影响。其中，在再入飞行过程中，飞行器机动飞行、大气扰流、壁面凸起或凹槽结构、外形非光滑转折等都会在飞行器绕流流场中产生诱导扰流，导致流场参数（压力、密度、速度、温度等）脉动，在飞行器表面形成复杂的脉动载荷环境。脉动压力环境产生的原因可分为附着湍流边界层、分离区和激波/边界层的相互干扰区域等3 种[1]。脉动压力作用于飞行器物面，诱导结构振动，可能导致飞行器结构破坏。同时，脉动压力可能诱发强烈的噪声环境，影响机载仪器设备的正常工作，对武器装备的环境适应性、可靠性、安全性等性能带来严峻考验。

飞行器绕流流场脉动载荷是诱导飞行器结构振动的主要激励源，是再入体结构设计中仅次于热环境的重要动力学环境因素[2]，是飞行器结构响应分析和动力学环境研究的重要依据。开展脉动压力环境预示研究，对于飞行器结构设计、结构动力学响应分析和环境适应性研究具有重要意义。文中对脉动载荷的形成机理、流动特征、测量方法、数值模拟方法进行了归纳总结，简要分析了脉动载荷定量评估的难点，并就飞行器脉动压力环境预示方法进行探讨。

1 脉动压力环境特点

到目前为止，一般认为包括脉动运动在内的湍流瞬时运动服从Navier-Stokes 方程（N-S 方程），而N-S 方程是具有非线性、时间相关特征的三维偏微分方程。

飞行器在大气中飞行时，由于空气黏性作用和飞行器表面黏性流体的无滑移边界条件，飞行器表面附近区域流动形成很强的速度梯度，在飞行器结构表面产生足够的涡量，形成较强的黏性应力。涡量在黏性作用下，扩散到流体内部，并向下游输运和耗散[3]。大量研究表明，飞行器近壁区域流动在运动过程中，旋涡不断经历形成、输运、破碎、合并和耗散等变化过程，涡的拉伸、破裂以及涡之间的相互干扰运动使得流场中速度、压力、温度和密度等流动参数不断变化，即产生脉动现象。流动呈现出非线性、随机、拟序结构等特征，如图1 和图2 所示。近壁面湍流拟序结构研究表明，湍流边界层的“猝发”（burst）、“下扫”现象直接影响壁面脉动压力环境[4]。飞行器近壁面区域流场呈现湍流状态，该区域流动参数随机变化诱导形成了脉动压力环境。

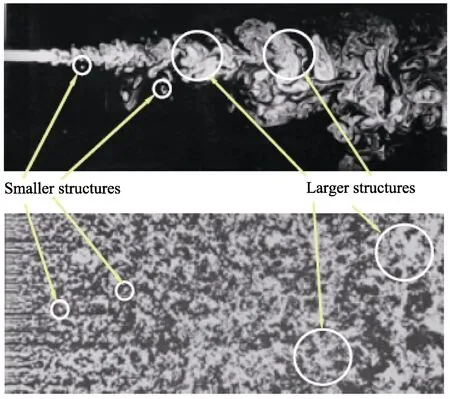
图1 湍流涡流动结构Fig.1 Structure of turbulence vortex

图2 湍流边界层(来自Van Dyke,1982)Fig.2 Turbulence boundary layer(From Van Dyke,1982)

脉动压力环境的特征主要有如下几点。

1）空间尺度范围大。湍流脉动的空间尺度包含了最大湍涡与最小湍涡尺度之间的所有空间尺度，其中最大湍涡尺度与流动特征密切相关，大涡主要受惯性影响，尺寸与流场大小相当，是引起低频、高幅脉动压力的主要原因。最小湍涡尺度由黏性决定，也就是取决于分子作用力，即取决于由Kolmogorov 定义的黏性耗散尺度（Kolmogorov 尺度）η∝(υ3/ε)1/4[4]，其中υ和ε分别为运动黏性系数和湍能耗散率。该尺寸可能只是流场尺度的1/1000 量级，是引起高频、低幅脉动压力的主要原因。由于湍流中包含了所有尺度的涡，脉动压力环境具有宽带特征。

2）时间尺度范围大。湍流脉动具有连续的频谱，脉动时间尺度涵盖最小湍涡时间尺度至最大湍涡时间尺度之间的所有时间尺度，最大湍涡的时间尺度为L/u′，最小湍涡的时间尺度为η/u′[4]，其中L和u′分别为最大涡尺度和大涡的特征速度，因此脉动时间尺度范围极大。

3）脉动量值小。与时均流场参数相比，飞行器绕流流场脉动量值非常小，约比时均参数小4～5 个数量级。实验研究很容易被背景噪声所湮没，同时测试仪器诱导的扰动也可能影响真实的脉动压力环境；而数值模拟必须保持低色散、低耗散的高精度计算格式，降低数值计算对脉动压力环境的影响。

4）三维性。湍流不稳定性源自于N-S 方程中非线性惯性项和黏性项之间的有旋、时间相关和全三维的相互作用。由于涡拉伸作用不可能存在于二维空间，相互作用中的有旋性、时间相关和三维性又是彼此关联的，二维近似处理不能合理解释湍流现象，因此湍流脉动呈现为强三维性。

5）随机性和输运传递特性。湍流是一种极不规则的流动现象，其不规则性不仅表现在速度、压强等流动物理量在时空中的不规则分布，还表现在不可重复性，脉动载荷具有很强的随机性。由于湍流中湍涡能量的传递和输运特性，而湍流脉动又被认为是流体波动，飞行器壁面脉动压力环境易受流场区域内、各边界处的扰动和限制条件的影响。

2 研究方法

理论分析、实验研究和数值模拟是研究脉动压力问题的三大手段。在研究早期，由于计算机能力的限制，各国的研究学者多以理论分析和实验研究为主。随着数值计算方法和计算机平台运算能力的不断发展，数值模拟分析在脉动压力环境预示中发挥了重要的作用。在流体力学和空气动力学发展过程中，学者们将3 种方法有机结合，互为补充，加深了对脉动压力问题的认识和理解。

2.1 理论分析

理论分析具有适用范围广、影响因素清晰等优点，能够用于指导后续的实验研究和验证性的数值模拟方法。对于特定的湍流脉动来说，同样可参照N-S方程进行定量分析。参照雷诺平均方法的思路，将可压缩瞬时流动的质量、动量方程中各瞬时物理量分解为时均量与相应脉动量之和，推导出脉动压力满足的偏微分方程，如式（1）所示。

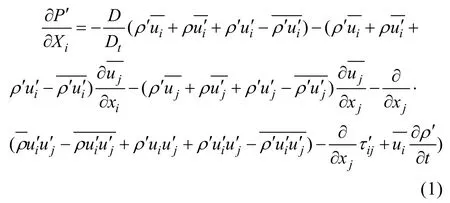
针对特定的湍流边界层流动，可对上述脉动压力方程等式右边各项进行量阶分析，消除某些对脉动压力影响较小的项，通过积分即可获得脉动压力的量阶估算式，结合一些实验数据，即可拟合建立脉动压力数值计算模型。

文献[5-6]以二维湍流边界层为例，通过分析式（1）右边各项的量阶，消除第二项、第五项小量纲项，联合求解边界层外缘处的平均流场和湍流脉动动能K的控制方程，最终获得了该湍流边界层内脉动压力的数值计算模型，如式（2）所示。

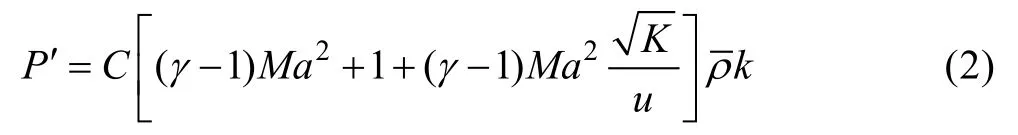
式（2）中的常数C可由实验数据拟合给出。国外就锥形、圆柱形等气动外形的脉动压力环境开展实验测量，对脉动压力方程式（1）进行简化，获得了适用于多种气动外形、流动马赫数等参数的脉动压力计算模型，有效地推动了脉动压力环境预示及动力学环境适应性研究。

复杂湍流流动中，脉动生成、输运、黏性和压缩性都会影响脉动压力环境，定量分析脉动压力各项量阶大小十分困难，甚至变得不可能。此外，某一脉动压力数值计算模型只适用于某些特定湍流现象，飞行器气动外形及飞行工况一旦发生变化，计算模型就不再适用。

2.2 实验研究

实验研究所得到的测量数据可信度相对较高，在脉动压力环境研究中发挥了重要作用。20 世纪60 年代以来，国外科学家就飞行器脉动压力问题进行了大量的实验研究，在实验测试方法、技术等方面进行了相应探讨[7-11]，如图3 所示。结合理论推导和实验数据，获得了适用于锥形、圆柱形等结构外形的脉动压力预示模型[12-13]，拟合了一系列针对特定外形的经验公式[14-15]，推动了飞行器动力学环境激励预示技术的发展。

文献[15]给出了附体湍流边界层流动的脉动压力预示公式，如式（3）所示。式（3）根据飞行器物面压力系数Cp(x)=[Pe(x)－P∞]/q∞预示均方根脉动压力系数，

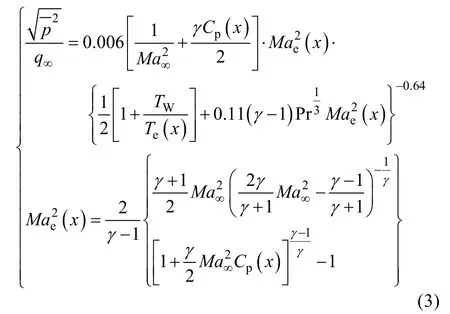
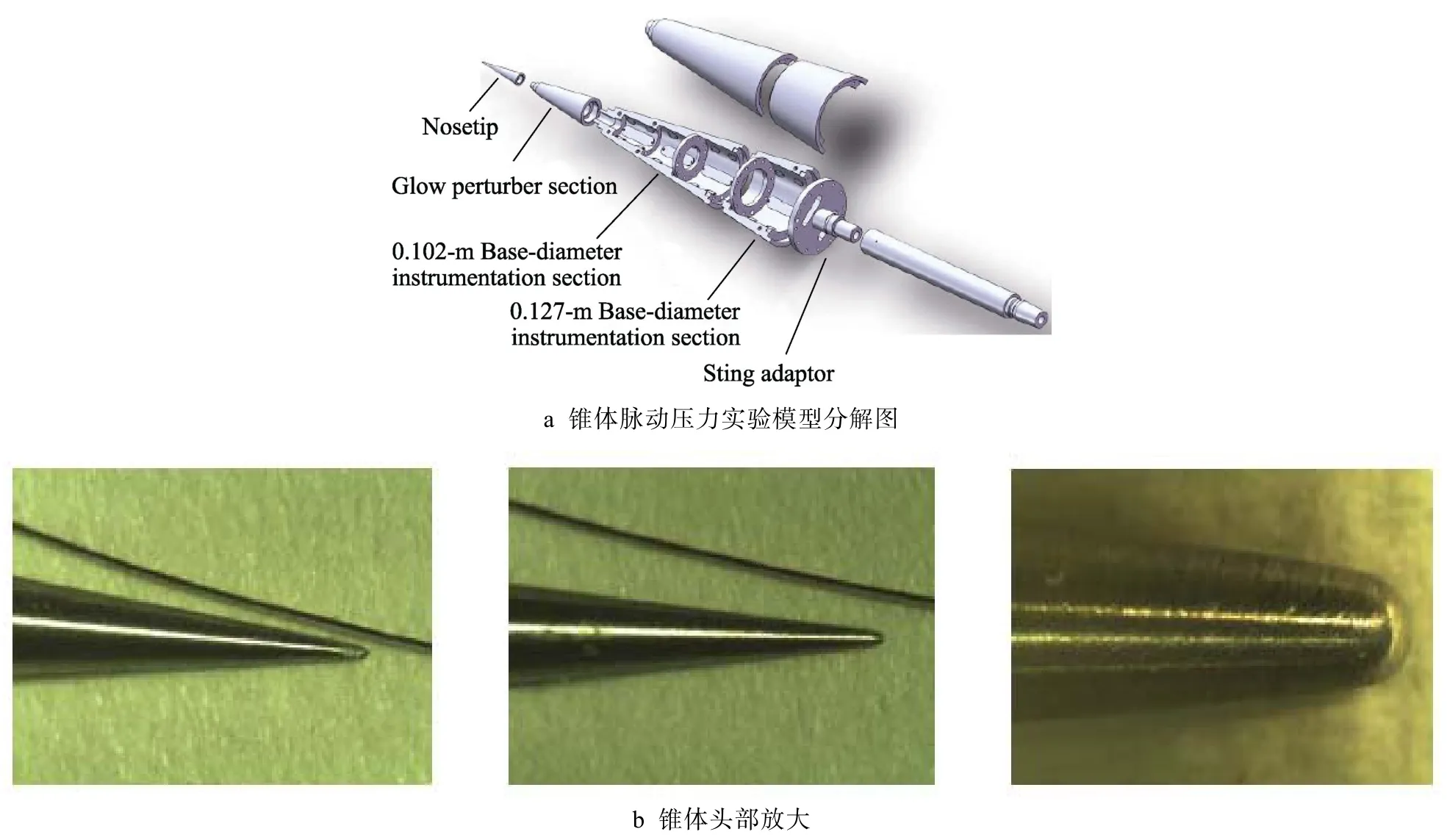
图3 风洞实验研究[10]Fig.3 Wind-tunnel test[10]:a) exploded view of experimental model of pressure-fluctuation cone;b) magnified cone head

式中：下标∞、e、W 分别为无穷远、附面层边缘和表面参数；x为沿壁面子午线距驻点的距离；γ为比热比；Pr 为普朗特常数。文献[15]同时也给出了功率谱密度与交叉功率谱密度的预示方法，并对某一球头双锥带控制翼的机动再入飞行器扰流流场的脉动压力环境进行预示，预示结果与实验数据吻合较好。

由于脉动载荷的小量值、输运传递、三维等特性，如果利用高动态压力传感器等类似的仪器进行实验测量，测量仪器的布置将对原有湍流流场引入新的扰动，如何降低测量仪器对湍流流动的扰动是脉动压力环境测量方法、测试技术中需要重点关注的问题。如果利用PIV 等流动显示技术对脉动压力环境进行测量，示踪粒子的跟随性、激光的频率都会成为限制脉动压力环境测量的因素。模型尺寸、流场扰动和测量精度等因素往往会成为实验开展的限制因素，同时实验研究还会遇到人力、物力、财力消耗大以及实验周期长的问题。

2.3 计算流体动力学（Computational Fluid Dynamics，CFD）

随着计算流体力学技术和计算机平台的飞速发展，越来越多的湍流问题可通过数值计算进行求解，利用数值求解再现并解释湍流流动现象。湍流的模拟是脉动压力环境数值计算的关键，因此脉动压力的数值求解方法与当前湍流数值模拟的方法相对应，主要包括：直接数值模拟（Direct Numerical Simulation，DNS）、湍流模式、大涡模拟（Large-Eddy Simulation，LES）、计算气动声学（Computational Aeroacoustics，CAA）以及基于上述方法建立的混合数值模拟方法。

2.3.1 直接数值模拟方法

直接数值模拟无需湍流模型化，通过直接求解三维非定常N-S 方程来模拟湍流瞬时流场。因此该方法的数值模拟可以精确获取每一瞬时流场上的全部信息，提供很多在实验上目前还无法测量的流场参量。

由于DNS 方法直接对N-S 方程进行数值求解，为了精确求解和刻画湍流流动现象，离散网格必须能够捕捉流场中所有尺度的流动结构，计算区域网格的尺寸在大到足以包含最大尺度涡的同时，还要小到足以刻画最小尺度涡的特征，大小尺度的比值随着Re的提高而迅速增大，整个计算域上的网格数量至少为Re9/4。另外，数值计算格式必须具有较高的精度，减少数值色散和耗散度，数值模拟过程中的时间长度要大于大涡的时间尺度，且计算的时间步长要小于小涡的时间尺度，总的计算量正比于Re3。在工程应用中的高雷诺数湍流流动中，湍流涡的时间、空间尺度范围较大。为了模拟最小尺度涡的流动，需要划分很精细的近壁面网格，消耗大量的计算时间和计算机容量，而这远远超过现有的计算机能力。

由于DNS 需要耗费庞大的计算资源和巨额的计算时间，在工程应用所关注的频域范围内（如随机振动所关心的频段为10～2000 Hz，噪声关心的频段为50～10 000 Hz），实际流动雷诺数为千万量级，其计算工作量更加惊人。目前难以直接应用于求解飞行器真实尺度的工程问题，但这不妨碍DNS 成为湍流机理研究的有力工具。随着计算机能力和求解方法的不断改进，DNS 目前不仅能求解压缩拐角、膨胀角等简单几何的激波边界层干扰问题[17-18]，也能求解来流马赫数为6，以头半径定义的来流雷诺数为10 000 的三维锥体转捩问题[19]（如图4 所示），求解问题的雷诺数也逐渐扩展到106量级[20]。可以预见，在未来的脉动压力环境研究中，DNS 将发挥越来越重要的作用。

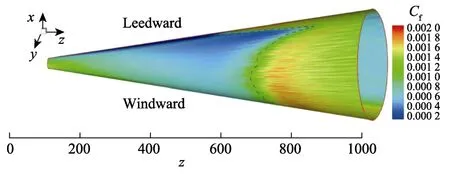
图4 采用DNS 方法求解三维锥体的转捩问题[18]Fig.4 The transition solution of three-dimensional blunt cone using DNS [18]

2.3.2 湍流模式理论方法

由于N-S 方程的非线性，通过解析方法来精确刻画三维全部湍流信息极其困难。在工程应用中，通常更关注湍流所引起平均流场的变化，即时均参量，因而工程数值仿真通常将非定常N-S 方程作平均处理。在三维N-S 方程计算模型中，雷诺平均法是目前使用最广的湍流数值模拟方法。该方法将湍流流动中的任何变参量都分解为平均值和脉动值等2 部分。雷诺平均法的核心不是直接求解瞬时的N-S 方程，而是求解雷诺平均N-S 方程，即RANS 方程。

由于RANS 方程中包含了脉动量乘积的时均值未知数，方程个数少于未知数个数，方程无法封闭。为了使方程封闭，需依据湍流理论知识、实验数据或直接数值模拟结果，根据经验数据、物理类比对雷诺应力作出各种假设，建立基于经验和半经验的本构关系，即通过建立湍流模型封闭RANS 方程。目前常用的湍流模型有雷诺应力模型和涡粘模型2 类。

无论采用何种平均方法和湍流模型，脉动运动的时空变化细节在平均的流场结果中都会被一概抹平，数值仿真结果无法获得全部的脉动运动信息，难以直接对脉动压力环境进行预示。工程上多采用数值模拟与经验公式相结合的方法[21]，通过RANS 方法求解时均流场，以流场信息作为输入，利用工程经验公式获得脉动压力环境特性的统计参数，如图5 所示。

2.3.3 大涡模拟方法

由于DNS 方法对流场全尺度的涡均进行模拟刻画，需要耗费大量的计算资源和时间。考虑到大涡与平均流场之间的相互作用比较强烈，大涡的形态和强度与流场特征密切相关，各向异性较强；而小涡主要是大涡之间非线性作用下的产物，受平均流场或边界特性的影响相对较小，可近似认为具有各向同性特征。因此LES 将比网格尺度大的湍流运动通过DNS求得，而小尺度涡对大尺度涡运动的影响则通过一定模型，通常是亚格子模型（多为Smagorinsky 模型，简称SGS 模型）来刻画。Ferzinger 对LES 给出了一个较为精确的定义：LES is same as any simulation of a turbulent flow in which the large-scale motions are explicitly resolved while the small-scale motions are represented approximately by a model (in engineering nomenclature) or parameterization (in the geosciences)。LES 是介于DNS 与RANS 之间的一种湍流数值模拟方法，与DNS 相比，LES 的计算量显著降低。

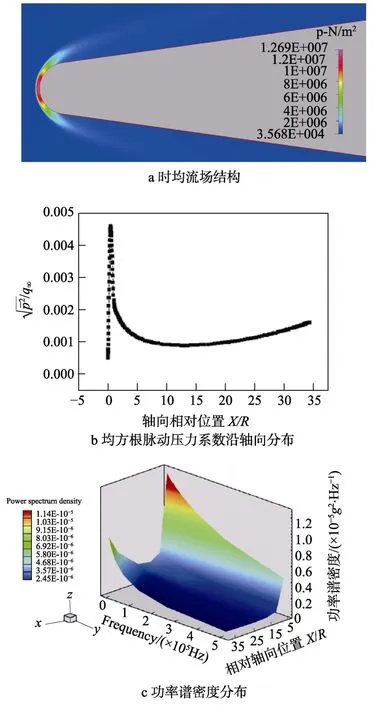
图5 基于半经验公式和时均流场的预示方法[21]Fig.5 The combination of time-averaged flow field and semi-empirical formula[21]:a) structure of time-averaged flow field;b) axial distribution of RMS fluctuating pressure coefficient;c) distribution of power spectral density

从飞行器动力学的环境适应性角度来说，关注的脉动压力主要集中在10～10 000 Hz 这一频段范围内。湍流流动中脉动信息的频率特性主要与大涡和小涡的时间尺度有关：其最高频率由最小湍涡的时间尺度η/u′≈(ν/ε)1/2决定，当来流速度约5000 m/s、特征长度约1 m、大气密度约0.5 kg/m3时，其最小湍涡对应的频率约为1012Hz 量级，远大于工程应用所关注的最高频率。因此脉动压力环境可利用大涡模拟进行数值求解。

LES 需选择合适的计算格式，格式选择不当可能会引起严重的数值耗散，甚至淹没亚格子（sub-grid）的作用。目前LES 在理论研究中多采用耗散性较小的高阶无耗散中心格式或紧致格式。此外，LES 的SGS 模型只对小尺度涡（各向同性的相似涡）进行模化处理，该尺度以上的湍涡信息仍需通过数值求解瞬时N-S 方程获得。DNS、LES 和RANS 等3 种数值求解方法的对比如图6 所示。

由以上可知，尽管LES 的计算量比DNS 要小几个数量级（NLES≈(0.4/Re1/4)NDNS）[16]，但也比RANS大出几个数量级。由于再入飞行器实际流动的雷诺数通常为千万量级，将LES 应用于工程脉动压力环境计算，仍将耗费巨大资源和时间。工程中应用LES，必须有足够的减小计算量的手段。为了弥补RANS方法捕捉分离流动的不足，同时提高LES 方法求解边界层流动的效率，RANS/LES 混合方法应运而生，并得到迅速发展。该类方法颇具代表性的是由Spalart[22]提出的脱体涡模拟法（Detached Eddy Simulation，DES），DES 结合RANS 和LES 的优点，对S-A 湍流模型进行长度尺度修正，近壁面通过RANS 求解附面层流动，远离物面的主流和分离区采用LES 方法进行求解，在降低计算量的同时，计算精度也令人满意。国内外学者采用该方法对钝体外形的亚声速、跨声速以及超声速流场[23-26]进行了数值模拟，背风面计算结果与风洞实验数据吻合较好，计算结果如图7 所示。

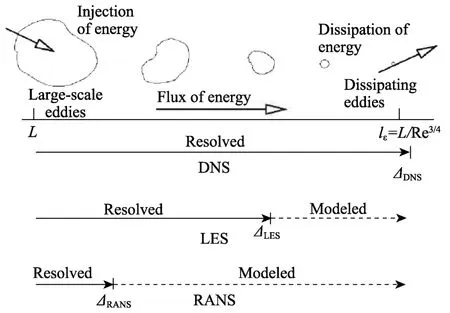
图6 3 种求解方法对比[16]Fig.6 Comparison of three solution[16]

图7 通过DES 求解得到的瞬时和时均流场的马赫数云图[24]Fig.7 Plots of Mach number for an in stantaneous and time-averaged flow field obtained by DES solution[24]:a) instantaneous flow field;b) time-averaged flow field

2.4 计算气动声学方法

飞行器绕流流场脉动是流动噪声的表现形式，即湍流流动同时形成湍流噪声[27]。湍流噪声随湍流流动的产生而产生，并随湍流流动的消失而消失，因而脉动压力环境也可从气动声学角度进行研究。气动声学的研究在20 世纪50 年代由Lighthill 从流体力学基本方程得到了对流场的外围声场的波动方程[28-31]，建立声比拟理论，并逐渐形成气动声学这一新学科。

目前，CAA 领域的计算方法主要包括两类[31]：一类是直接模拟，即在一定计算域内运用经过特殊处理的CFD 方法直接计算近场的流场和声场，包括上述介绍的DNS、LES 及RANS，然后用Kirchhoff 积分外推到远场；另一类是基于Lighthill 气动声学理论的声比拟方法，此法将流场与声场分开计算，近场流场由LES、RANS 计算获得，远场由各种理论模型得到。目前主要的方法有Lighthill 声比拟、涡声理论、Hardin 和Pope 的分裂方法、有声源项的线化欧拉方法、声扰动方程等。采用CAA 方法求解得到的增升装置瞬态摄动压强流场如图8 所示。

CAA 主要关注湍流噪声（脉动压力）的非定常流动机理、声源确定、声与流体的相互作用、声波的传递等研究。利用CAA 数值方法求解飞行器近场声场，获得飞行器动力学环境（振动）相应的环境激励源——脉动压力环境，即CAA 可应用于飞行器绕流流场脉动压力环境研究。如通过RANS 方法计算近场流场声源，利用Lighthill 方程计算其脉动密度，进而获得脉动压力环境，声学方程见式（4）。

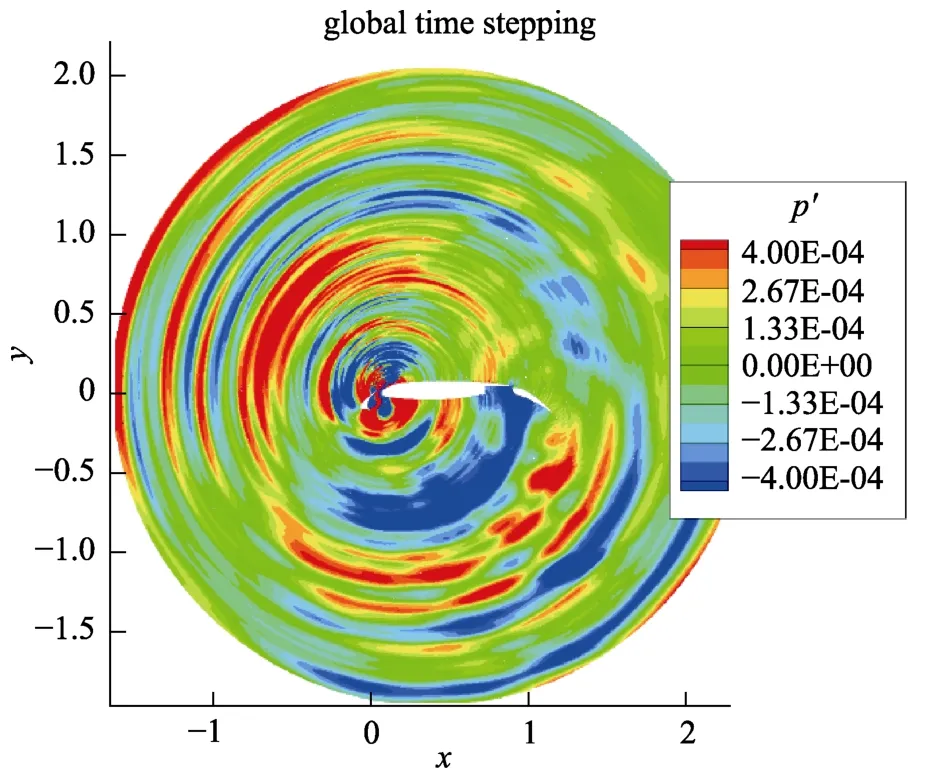
图8 CAA 方法求解的瞬态摄动压强流场[32]Fig.8 Instantaneous perturbations pressure flow field using CAA[32

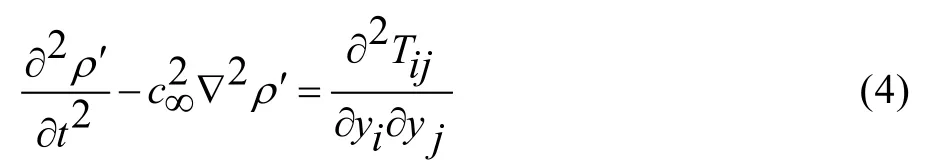
式中：ρ′=ρ-ρ0，。

CAA 采用的数值方法与CFD 方法存在紧密联系，特别是它们在湍流脉动信息数值处理方面，同DNS 和LES 类似，CAA 在数值耗散、色散、高精度离散格式、多尺度等方面具有很高的要求。此外，CAA边界条件（需要无反射边界条件）的要求十分苛刻。利用CAA 数值求解飞行器绕流流场脉动压力环境仍需耗费较大计算资源和计算时间，工程实现存在较大难度。

3 脉动压力工程研究与应用可行途径

脉动压力环境是飞行器飞行任务剖面主要的动力学环境激励源，为飞行器振动噪声环境适应性研究提供数据输入，直接影响飞行器动力学结构响应。由于再入飞行器飞行马赫数高，绕流流场雷诺数高达108，如果利用DNS 数值求解飞行器绕流流场脉动压力环境，其计算量约比雷诺数105的流动大9 个量级，将极大耗费计算资源和计算时间，短期内难以实现工程研究与应用，但应用前景诱人。

为了实现计算效率和计算精度的平衡，LES 方法和以DES 方法为代表的混合方法不断发展，该方法已应用于求解雷诺数约为107的湍流流动。然而，由于LES 和DES 方法分别利用亚格子模型和RANS 方法求解湍流边界层，它更适用于模拟远场流动分离、尾迹涡等脱体涡分离流动。对于飞行器再入过程中湍流边界层占主导的脉动压力环境问题而言，难以实现准确的脉动压力环境预示。

对于CAA 而言，多采用基于声比拟的方法，将流场和声场分别求解，通过流场结果构造声源，再利用声传播方程获得远离物面流场的脉动压力环境。也就是说CAA 方法在不额外增加较大计算量的前提下，能够准确地获得远场的脉动压力，但对于物面处的脉动压力环境预示多取决于求解流场采用的方法精度，对于预示物面的脉动压力提升有限。

根据以上分析可知，由于飞行器绕流流场雷诺数高，脉动压力环境具有多尺度、量值相对较小等特征，湍流脉动数值模拟方法和技术尚处于湍流流动机理分析和研究阶段，短期内无法解决飞行器绕流流场脉动压力环境工程问题。分析现有的飞行器脉动压力环境预示技术，可能存在如下几条途径。

1）风洞实验测量预示方法。国内外就飞行器脉动压力环境的风洞实验测量技术和方法进行了大量研究，成功运用于脉动压力环境预示。由于风洞实验状态有别于飞行器飞行状态（雷诺数、密度等），风洞实验预示的脉动压力环境与飞行器真实飞行脉动压力环境存在一定差异，实验测量数据处理和修正尚需开展深入研究。

2）基于半经验公式和时均流场的预示方法。针对典型飞行器的气动外形和飞行工况，国内外已经研究、推导和构建了丰富的基于时均流场的脉动压力半经验公式预示方法，极大地推进了飞行器脉动压力环境预示研究进展。由于这类方法在很大程度上依赖于半经验公式对气动外形和飞行参数的适应性，需针对特定飞行器和飞行工况的半经验公式进行适应性研究和改进，提高预示精度和准确性。

3）基于DNS 的数值模拟方法。由于飞行器再入过程中速度高，雷诺数大，物体表面的涡尺度较小，只有精确捕捉小尺度的涡才能实现脉动压力环境的准确预示。从数值模拟方法原理来看，目前只有DNS方法才能实现物面小尺度涡的准确刻画。但由于其庞大的计算量，目前无法解决高雷诺数复杂三维外形的脉动压力问题。随着计算能力的提升，数值方法的改进，目前已经可以求解三维锥体转捩问题，雷诺数也逐渐扩展到106量级，DNS 方法未来在脉动压力环境问题研究中有着光明的前景。