解卷积主动声呐目标回波高分辨时延估计技术

苍思远 生雪莉 董 航 郭龙祥

(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

(哈尔滨工程大学海洋信息获取与安全工信部重点实验室 哈尔滨 150001)

(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

主动声呐系统通过测算目标回波的时延信息来实现对水下目标的探测[1,2]。我国近海多为浅海环境[3]，声信道复杂多变，多途扩展严重。工作在浅海环境的主动声呐系统受复杂海洋信道的影响极大，探测变得十分不稳定。因此，研究一种可以抑制复杂多途信道影响，同时还可以获得高分辨时延估计结果的信号处理技术变得十分迫切。

2016年，Yang[4]将解卷积思想与水声阵列信号处理相结合，提出了解卷积波束形成技术，不但拥有较高的目标方位估计分辨率和空间增益，而且具有常规波束形成的稳健性。从声呐系统接收端的角度考虑，目标的状态信息与水声环境为耦合关系，如能通过解卷积等技术“解耦合”掉环境的干扰，那么探测水下目标则会变得稳定、高效。

在水下声学领域，解卷积时延估计，少有研究成果发表。匹配滤波[5,6]、广义互相关[7]等传统时延估计技术主要依靠调频信号良好的自相关性能进行能量检测，其相关衍生方法因运算复杂度低，工程实现方便得到了广泛应用。Chandran 等人[8]为了检测水下掩埋雷，提出一种逐帧处理的匹配滤波器，所形成声呐图像上的高阶矩信息被当作目标识别的关键因素。Benesty等人[9]提出一种线性插值互相关时延检测器。多通道互相关系数的联合处理，提高了室内声学麦克风阵列的时延估计分辨率。

如果放宽对发射信号波形的限制，那么自适应类方法进入了我们的视线。文献[10]提出对自适应滤波器的长度进行限制，研究了一种基于特征值分解的频域LMS时延估计算法，被应用到了室内声场的盲系统辨识中。但是，自适应滤波器的收敛性能受到迭代步长的影响较大。如果迭代步长选取不当，则会使算法遇到难以收敛的问题，时延估计算法变得十分不稳定。

近年来，基于欠奈奎斯特采样定律的压缩感知技术受到关注。压缩感知的分支—稀疏表示理论，具有分辨率高，信号重构误差小等特点[11–13]。Meng等人[14]对基追踪降噪稀疏表示模型和宽带积分字典进行了研究，提出一种具有高分辨性能的水下目标回波参数估计方法，对水下目标的几何散射回波和弹性散射回波进行了有效地估计和分离。但它分析的是近距离的探测场景，并没有考虑中远距离情况下海洋信道的影响。

针对浅海复杂声信道环境中的目标回波时延估计问题，本文基于稀疏表示理论和解卷积思想，提出一种可以广泛应用在中远程探测场景的高分辨时延估计技术。本文所提出的解卷积时延估计技术，首先用亮点模型近似表示水下尺度目标的散射特征，然后结合稀疏水声信道的特性，引入Toeplitz算子，线性地表示发射信号与广义信道冲激响应的卷积过程。最后通过交替方向乘子算法(Alternating Direction Method of Multipliers, ADMM)优化框架，解算出目标回波时延的估计值。通过加权迭代策略设置正则化参数，进一步地解耦合信道，重构回波到达时刻。目的是在获得高分辨时延估计结果的同时，突出信道冲激响应的主途径，抑制或忽略其他冗余的弱途径。以此来克服多途信道的影响，实现稳定的水下尺度目标的探测。

2 物理背景与数学模型

2.1 水声信道模型

水声信道是具有频率选择性衰落的扩展信道。从线性系统的角度分析，水声信道可以看作是若干个不同幅度、不同时延的脉冲函数的叠加，表达式为

2.2 目标回波亮点模型

水下目标一般可以看作是一个有尺度的水下几何体，它的不同位置对信号的散射强度不同，类似地，散射信号到达接收机的时间也不同。近年来，水声目标的亮点模型[15]备受关注。亮点模型主要把水下目标的几何散射特性近似地看作是若干个亮点。水下目标的第i个亮点的幅频与相频特性可以用亮点模型的传递函数表示

3 基于稀疏表示的目标回波解卷积时延估计技术

目标回波信号可以理解为发射信号受到双程信道冲激响应和目标信道冲激响应共同作用的输出。接收信号的表达式为

4 优化问题的解决方案

前文构建了基于稀疏表示的目标回波解卷积时延估计模型，而求解回波时延的估计值所利用的LASSO模型则可以简化为求解凸优化问题。人们解决凸优化问题的常用手段，是斯坦福大学开发的CVX工具包[18]。但是，水下声学平台对近海、港口等区域进行监测通常会有数据实时处理的需求，因采集数据量较大，CVX工具包的计算能力稍显不足。这里，采用另外一种基于分布式迭代优化策略的快速求解算法——ADMM[19]。

4.1 ADMM的展开式与推导

ADMM解决优化问题的思路是把一个大问题拆分成若干个容易解决的小问题，通过迭代优化，交替求解，十分高效。

涉及到具体问题，分析如式(13)的代价函数

值得注意的是，ADMM算法在迭代运算的过程中，迭代停止条件的设置十分关键。根据文献[19]，本文设置的迭代停止条件为本次估计值与上一次估计值的差小于10–4。

4.2 基于加权迭代策略的正则化参数设置方法

在利用ADMM求解时延估计值的过程中，正则化参数λ 的选取十分关键。合适的正则化参数可以较为有效地抑制噪声影响，提高时延估计的分辨率。文献[20]为了增强所求得解的稀疏度，提出了一种基于加权L1范数的稀疏优化模型。受此启发，本文在实际问题中，引入基于加权迭代策略的正则化参数设置方法。一方面可以抑制噪声的影响，最主要的是通过给不同的时延估计值添加权系数，弱化多途产生的虚假时延估计值，突出强化主途径，抑制浅海复杂声信道的影响，准确地解算出回波到达的时刻。

定义一个加权系数向量b，令其与正则化系数的初值 λ0相乘以实现加权。第ℓ 次迭代时，正则化参数λ 的第i个元素具有这样的表达式

5 数值仿真与实验数据分析

5.1 仿真数据分析

本节通过仿真数据来验证解卷积时延估计方法的有效性。仿真态势如图1所示，声源的深度为20 m，发射2～4 kHz的线性调频信号，脉宽为62.5 ms，采样频率16 kHz，水深100 m，目标的深度25 m，与声源的水平距离为3000 m。解卷积时延估计方法的流程如表1所示。利用射线声学理论，采用海试实测的负梯度声速分布，生成的发射声源到目标处的信道如图2(a)所示。根据亮点模型的假设，目标在这里被设定为一个具有3个亮点的水下尺度目标，利用式(5)得到广义信道冲激响应如图2(b)所示。将匹配滤波方法与本文所提解卷积时延估计方法进行对比。噪声干扰为高斯白噪声，信噪比设置为5 dB。

通过观察图2(a)和图2(b)发现，根据海试实测声速分布及声源和目标的态势，仿真所生成的单程信道含有较多的多途，广义信道的多途扩展则更为严重。根据图3，匹配滤波估计得到的时延结果含有较多的伪峰，没有采用加权迭代策略设置正则化参数的解卷积时延估计方法虽然准确估计出了回波到达时刻，但是仍含有较多幅度较低的途径。采用加权迭代策略的解卷积时延估计方法，只保留了回波到达的主途径，其他途径都已经被加权系数抑制掉。

表1 解卷积时延估计方法流程

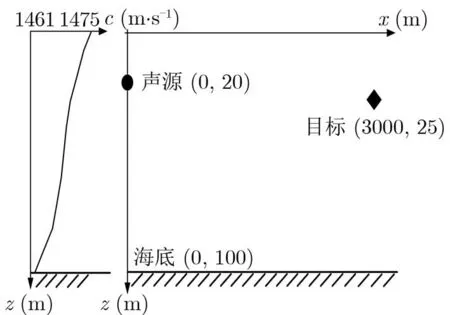
图1 主动声呐探测目标仿真态势图及声速剖面

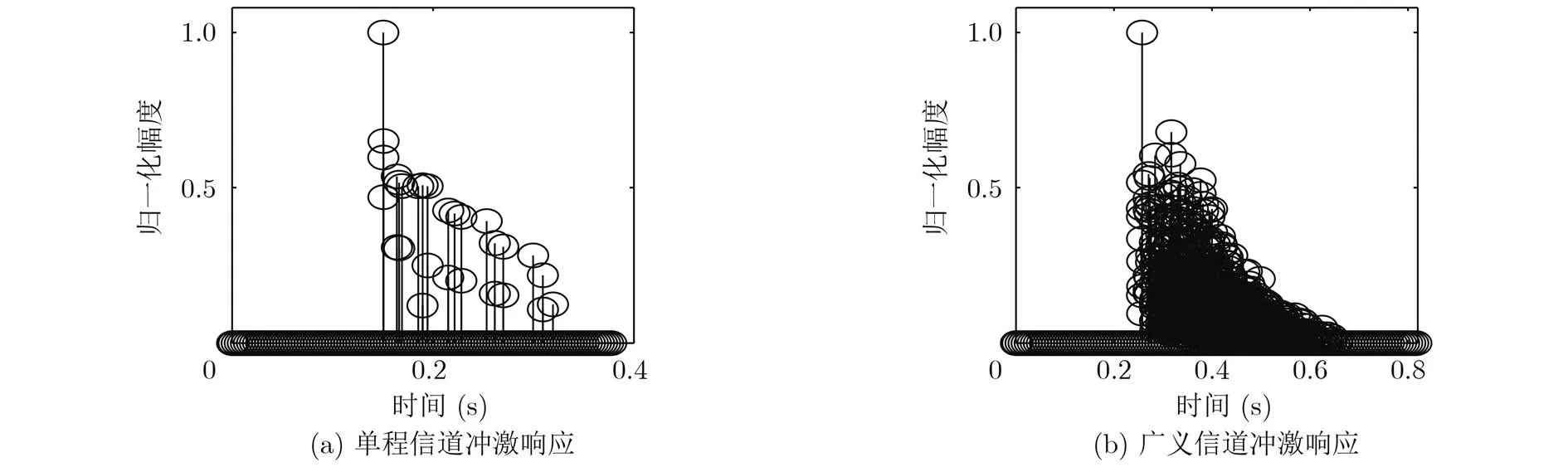
图2 单程信道冲激响应和广义信道冲激响应

基于同样的仿真态势，将发射信号替换为中心频率为4 kHz，脉宽为62.5 ms的正弦信号，信噪比同样设置为5 dB，目标回波时延估计结果如图4所示。由于正弦信号的自相关性能较差，根据图4，匹配滤波已经很难正确地估计出回波的到达时刻。而采用加权迭代策略的解卷积时延估计方法依然只保留了能量最强的主途径，拥有和线性调频信号作为发射信号时一样的分辨率。可以看出，解卷积时延估计方法对发射信号的波形没有限制，适用性较广。

定义时延估计均方根误差(Root Mean Square Error, RMSE)为

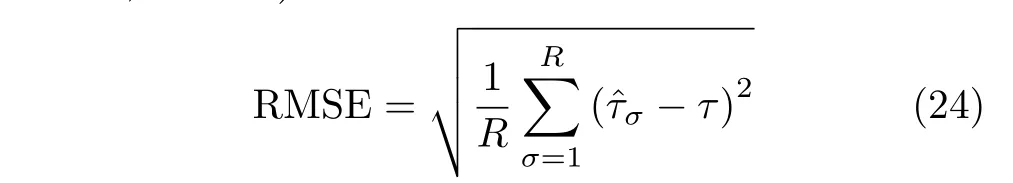
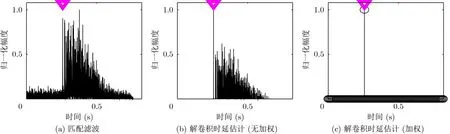
图3 发射信号为线性调频信号，目标回波时延估计结果

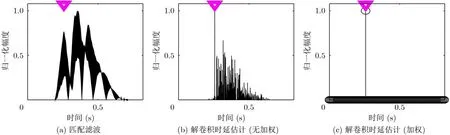
图4 发射信号为正弦信号，目标回波时延估计结果

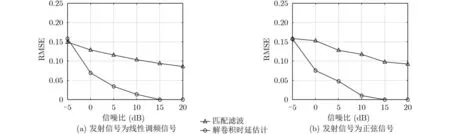
图5 不同信噪比下时延估计的RMSE曲线

分辨率方面，仍以5 dB的信噪比的仿真情况为例。定义时延估计的分辨率为主途径–3 dB主瓣宽度所对应的脉宽。为了公平地比较时延估计的分辨率，我们将两种方法中错误估计的结果去掉，只考察估计正确的结果，计算–3 dB主瓣宽度所占据的平均采样点数。结果如表2和表3所示。发射信号为线性调频信号时，匹配滤波方法的时延估计分辨率与发射信号带宽B有关(瑞利限，1/B)，为0.514 ms；发射信号为正弦信号时，匹配滤波方法的分辨率较差，为36.3 ms。解卷积时延估计方法，发射信号采用线性调频信号或正弦信号，–3 dB主瓣宽度均只占据1个采样点，分辨率为0.063 ms，突破了1/B的限制。

5.2 实验数据分析

为了进一步验证解卷积时延估计方法的性能，本文在哈尔滨工程大学的信道水池开展了目标回波时延估计实验。信道水池的水面和池底对发射信号的反射较多，能够较好地模拟复杂的广义信道冲激响应，故用声源发射信号来模拟目标回波。声源的深度为2.5 m，水听器的深度为2 m，水听器与声源相距12 m，信道水池水深5 m，实验设备的布放连接方式和具体实验态势如图6所示。

表2 发射信号为线性调频信号，时延估计分辨率(SNR=5 dB)

表3 发射信号为正弦信号，时延估计分辨率(SNR=5 dB)

首先以4～8 kHz的线性调频信号作为发射信号，脉宽200 ms，整个系统的采样频率为18 kHz。利用匹配滤波和采用加权迭代策略的解卷积时延估计方法分别对接收信号进行时延估计，结果如图7(a)所示。匹配滤波和解卷积时延估计方法所得到的信道主途径的时延估计结果一致，但是匹配滤波方法所得结果中有较多旁瓣，这是由于信道水池的复杂多途结构中众多弱小的途径，经过相关运算累加所致。反观解卷积时延估计方法，只保留了两个能量较强的途径，其他较弱的途径则已被加权迭代策略抑制掉。可以看出，解卷积时延估计方法在环境解耦合方面能力较强。

分辨率方面，匹配滤波的估计结果中主途径–3 dB主瓣宽度所占据的采样点数为5个，分辨率为0.27 ms，与线性调频信号的瑞利限1/B(B=4 kHz)基本保持一致。解卷积时延估计方法，主途径的–3 dB主瓣宽度依然是1个采样点，分辨率只与系统采样频率有关，为0.056 ms。

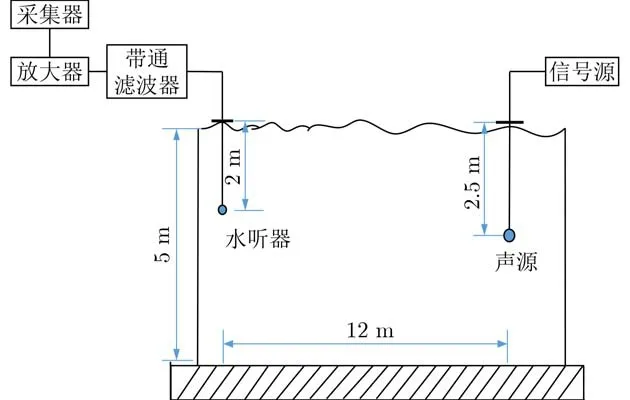
图6 信道水池实验态势图

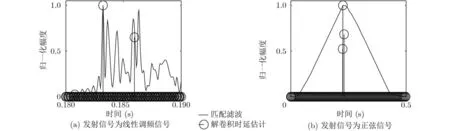
图7 信道水池实验数据时延估计结果

接下来，将发射信号换成中心频率为6 kHz的正弦信号，脉宽和系统的采样频率依然是200 ms和18 kHz。利用匹配滤波和采用加权迭代策略的解卷积时延估计方法分别对接收信号进行时延估计，结果如图7(b)所示。正如仿真分析的那样，由于正弦信号的自相关函数主瓣较宽，匹配滤波方法得到的时延估计结果，分辨率较差。在图7(b)中，匹配滤波方法得到的–3 dB主瓣宽度所占据的采样点数为2112个，分辨率为132 ms。解卷积时延估计方法依然可以抑制掉多途中较弱的成分，只保留能量较强的3个途径。主途径的–3 dB主瓣宽度依然只占据的1个采样点，分辨率为0.056 ms。实验数据进一步验证了解卷积时延估计方法对发射信号的波形无限制的结论。

6 结束语

浅海声信道多途扩展严重，传统时延估计方法抑制多途干扰的能力有限，且分辨率受瑞利限的制约，探测水下目标的能力受到严重影响。针对此问题，本文提出一种基于稀疏表示理论的解卷积高分辨时延估计技术，可广泛应用于浅海中远程目标探测场景。把回波时延估计的问题表示为凸优化问题，通过迭代运算可以获得全局最优解，时延估计精准，在信噪比大于10 dB时，可以达到零误差；通过加权迭代策略设置正则化参数，克服了多途信道的影响；时延估计的分辨率突破了瑞利限，在信道水池的实验环境下，达到0.056 ms；对发射信号的波形没有限制，适用性广。仿真和水池实验数据验证了解卷积时延估计技术的有效性。