基于参考距离史的多子阵SAS成像算法

吴浩然 张非也* 唐劲松 佟怡铄

①(海军工程大学电子工程学院 武汉 430033)

②(海军工程大学科研处 武汉 430033)

1 引言

合成孔径声呐[1](Synthetic Aperture Sonar,SAS)是一种起源于合成孔径雷达[2,3](Synthetic Aperture Radar, SAR)技术的高分辨成像声呐。与SAR不同，由于水中声速的低速性，SAS首先需要采用多子阵技术才能获得实用的测绘速率，然后还需要考虑在发射和接收期间声呐前进的距离才能够获得足够精确的距离史，这就是所谓的“非停走停”模式[4]。受“非停走停”的影响，SAS每个子阵的精确距离史既不是单基站SAR的单根号形式，也不是双基站SAR的双根号形式，而是一个非常复杂的表达式[5]，那么如何获得多子阵SAS的2维谱，成为研究多子阵SAS成像算法的关键。

目前多子阵SAS 2维谱的获取方法主要有3种。第1种方法是用2维谱的数值解代替解析解[6]。虽然该方法的精度较高，但是数值计算过程和逐阵元单独成像特点导致成像效率较低。第2种方法是将精确距离史展开成方位时间的幂级数形式后，用级数反演的方法求得2维谱的解析解[7,8]。该方法的优点是不需要关心精确距离史表达式的形式，且谱的精度可以通过调节幂级数的阶数进行控制，但是存在2维谱表达式复杂和需逐阵元单独成像的问题。第3种方法通过忽略“非停走停”时间的孔径依赖性将精确距离史变成双根号形式，再利用修正偏置相位中心技术[9](Displaced Phase Centre Antenna,DPCA)和驻定相位原理(Principle Of Stationary Phase, POSP)获得2维谱的解析解，称为修正DPCA方法。这种方法的优点是只需要进行一次成像处理，效率较高，但是忽略了“非停走停”时间的孔径依赖性，可能带来较大的时延误差，从而影响成像质量。

为了解决忽略“非停走停”时间的孔径依赖性带来时延误差的问题，本文提出一种基于参考距离史的多子阵SAS成像算法。

首先利用参考子阵与各子阵之间的平移关系，推导每个子阵的近似距离史，解决“非停走停”时间的孔径依赖性需要被近似的问题。由于每个子阵几乎是同时接收到同一脉冲的回波，有相同的“非停走停”时间，因此用一个子阵的精确距离史推导其他子阵的距离史，就能够解决“非停走停”时间孔径依赖的问题。本文将基线长度等于0的子阵定义为参考子阵，其距离史为参考距离史(Reference Range History, RRH)。在方位/距离坐标系中将RRH沿方位向平移某个子阵的半个基线长度，沿距离向平移该子阵的相对距离偏移量，把平移后的距离史作为该子阵的近似距离史。该子阵与参考子阵在接收阵上位置不同导致的差分距离弯曲，是该近似距离史误差的主要来源，但是文献[10,11]的分析结果表明同一条接收阵的差分距离弯曲可以忽略。

然后将每个子阵信号搬移至相同的波束中心距离，再通过方位重构将欠采样的多子阵信号转变成满足采样定理的等效单基站信号。由于RRH平移得到的近似距离史具有单根号形式，其对应信号的相位驻留点是可解析的，因此可以直接通过POSP求得每个子阵2维谱的解析解。但是每个子阵信号在方位向是欠采样的，需要将每个子阵回波搬移至相同的波束中心距离后，再进行方位重构才可以得到满足采样定理的等效单基站信号。这时单基站成像算法如距离多普勒算法[12](Range Doppler Algorithm, RDA)、线频调变标[13](Chirp Scaling Algorithm, CSA)和波数域算法[14](ω-K Algorithm,ωKA)等直接处理等效单基站信号，就可以得到多子阵SAS的成像结果。最后，通过仿真实验和实测数据结果检验算法的有效性。

本文内容组织为：第2节给出基于RRH的近似距离史；第3节推导多子阵SAS 2维谱解析解；第4节通过仿真实验和实测数据验证算法的有效性；第5节进行总结。

2 基于参考距离史的近似距离史

2.1 精确距离史

多子阵SAS的几何模型如图1所示，其中x轴与SAS的前进方向平行，y轴在水平面内与x垂直, z轴的正方向垂直向下。假设t是慢变时间，v是SAS的速度，h是SAS距海底的高度，r是目标与航迹之间的最短距离，di表示第i个接收阵与发射阵之间的基线长度，θr是r与z轴的夹角，θy是SAS的偏航角，θp是SAS的俯仰角，那么多子阵SAS精确距离史[6]为

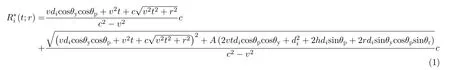
2.2 近似距离史

图1 斜视多子阵SAS模型

图2 参考阵与接收阵i的精确距离史曲线

为了定量地评估近似距离史误差的大小，进行仿真实验。假设SAS中心频率为80 kHz，发射信号带宽为20 kHz，脉冲宽度为20 ms，脉冲重复间隔为0.406 s，接收阵元长度为0.07 m，发射阵长度为0.14 m，接收阵元个数为29，水中声速为1500 m/s，SAS速度为2.5 m/s，测绘带宽度为[66 290] m，声基阵如图1所示。不失一般性，选取基线最长的子阵作为研究对象，在不同斜视角下比较修正DPCA和本文方法的误差大小，结果如图3所示。

对比图3(a)和图3(c)，可以看出修正DPCA方法的误差主要集中在远距离处，随斜视角的变化较大；同样地对比图3(b)和图3(d)，发现RRH方法的误差虽然也主要集中在远距离，但是在相同斜视角下误差明显小于修正DPCA方法。为了定量地比较两种方法距离史误差的大小，用波长λ分别对图3(a)、图3(b)、图3(c)和图3(d)进行测量，得到误差的最大变化量分别为0.067λ, 0.040λ, 0.449λ和0.080λ。从测量的结果可知，当斜视角从4.4°变化到12.4°时修正DPCA方法的误差从0.067λ变化到0.449λ，超过了λ/8，可能对成像结果产生影响；而RRH方法的误差仅增加了0.040λ。因此该仿真结果表明：(1)RRH方法得到的近似距离史能够满足成像要求；(2)RRH方法的误差小于修正DPCA。

3 多子阵SAS 2维谱

3.1 各子阵2维谱

图3 在不同条件下修正DPCA和RRH方法的误差

虽然式(10)能够给出每个子阵的2维谱解析解，但是在方位向每个子阵是欠采样的，还需要通过方位重构算法将多子阵信号转换成单基站信号，以满足采样定理。

3.2 等效单基站2维谱

为了保证方位重构时在不同子阵中相同目标的信号能够位于同一个距离门，需要通过相位校正和时延校正的方式将每个子阵信号搬移至相同的波束中心距离。其中相位校正的实质是补偿式(11)中第5项，可以在2维时域通过逐子阵逐脉冲地相位相乘实现，相位相乘因子为

时延校正的实质是校正式(11)中第6项表示的距离空变型变量。对于距离空变的变量，插值是最精确的校正方法，但是计算量较大。由于∆ Ri(r)是弱距离依赖的，因此可以用参考距离rref上 的∆Ri(rref)代替整个场景的 ∆Ri(r)。这样就可以利用傅里叶变换的位移/调制性质，在距离频域用一个正指数线性相位函数与回波信号相乘的方式实现时延校正，该线性相位函数为

然后直接用RDA, CSA和RMA等单基站成像算法处理等效单基站信号，将可以得到多子阵SAS的成像结果。

4 实验验证

4.1 仿真实验验证

为了验证本文算法的有效性，本节进行计算机仿真实验。系统参数与2.1节所示仿真一致，成像几何模型如图1所示，目标的距离史由精确距离史式(1)给出。假设仿真场景内有5个反射系数为1的理想点目标，其坐标分别为P1(–3 m, 259 m, 0 m),P2(–3 m, 265 m, 0 m), P3(3 m, 265 m, 0 m), P4(3 m,259 m, 0 m) 和 P5(0 m, 262 m, 0 m)。这里选取非线性频调变标算法(Non-Linear Chirp Scaling Algorithm, NLCSA)[15]单基站成像算法分别处理基于RRH和基于修正DPCA的等效单基站信号，结果如图4所示。

对比图4(a)和图4(c)，可以看出在修正DPCA方法的成像结果中虚假目标的数量和能量都随斜视角的增大而增加，表明该方法受斜视角的影响较大；同样地对比图4(b)和图4(d)，发现斜视角从4.4°增加12.4°时RRH方法的成像结果始终没有出现明显的虚假目标，表明RRH方法受斜视角的影响很小。为了更详细地比较两种方法的成像质量，将图4各个子图中的P5提取出来，做方位向剖面如图5所示。然后分别对P5方位向和距离向3 dB主瓣宽度(Impulse Response Width, IRW)、主副瓣比(Peak SideLobe Ratio, PSLR)和积分旁瓣比(Integration SideLobe Ratio, ISLR)进行测量，结果如表1所示。

通过图5(a)和表1可以看出，当斜视角为4.4°时RRH方法相对于修正DPCA方法的优势并不明显，RRH方法仅方位向PLSR稍好于修正DPCA方法。但是当斜视角增加到12.4°时，通过图5(b)和表1可以看出RRH方法的虚假目标能量依然没有增加，而修正DPCA方法虚假目标的能量却增加了接近30 dB。由于修正DPCA方法虚假目标能量的大幅提高，导致表1中斜视角为12.4°时修正DPCA方法的方位IRW变好。

上述仿真结果表明，RRH方法的成像效果在斜视角4.4°和12.4°时都好于修正DPCA方法，验证了本文提出算法的有效性。

4.2 实测数据验证

图4 在不同斜视角下修正DPCA和RRH的成像结果

图5 不同斜视角下P5的方位向剖面

表1 P5的成像质量参数比较

本节采用干涉合成孔径声呐在中国南海试验过程中录取的回波数据进行验证。由于该声呐属于拖曳式干涉合成孔径声呐，运动姿态比较稳定，斜视角比较小。这里选取斜视角为1°的回波数据，分别用修正DPCA方法和RRH方法处理，得到成像结果分别如图6(a)和图6(b)所示。对比修正DPCA和RRH方法的成像结果，特别是图6中红色圆圈标记部分，可以明显看出RRH方法的成像结果比修正DPCA的轮廓更加清晰，验证了本文算法的有效性。

5 结束语

为了解决现有多子阵SAS成像算法忽略了“非停走停”时间的孔径依赖性，导致成像结果变差的问题，本文提出了一种基于RRH的多子阵SAS成像算法，并通过仿真实验和实测数据检验了算法的有效性。本文提出的算法不但能够处理斜视多子阵SAS，还能够处理正侧视多子阵SAS，此外还能够与单基站RDA, CSA,NLCSA和RMA等多种成像算法结合获得成像结果。

图6 修正DPCA和RRH的实测成像结果