基于分层贝叶斯Lasso的稀疏ISAR成像算法

杨 磊 夏亚波 毛欣瑶 廖仙华 方 澄 高 洁

(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

1 引言

逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)作为一种主动的微波探测手段，可实现针对非合作运动目标的全天时、全天候、远距离、高分辨成像探测。ISAR通过发射并接收大带宽信号获得距离向高分辨，通过在相干积累时间(Coherent Processing Interval, CPI)内合成一定目标视角变化的多脉冲回波获得方位向高分辨[1,2]。典型的ISAR系统常放置于地面，用于监测空中威胁目标。由于空中目标相对空域稀疏，ISAR接收回波信号具有稀疏特性，可利用压缩感知(Compressed Sensing, CS)理论，以远低于奈奎斯特采样率的回波数据恢复ISAR成像结果[3]。压缩感知理论由Donoho[4]提出，该理论基于目标稀疏性假设，可实现图像或信号的稀疏重构，从而建立了由低维观测数据精确恢复高维目标信号的理论体系[5]，在雷达信号处理领域应用广泛。

压缩感知理论框架下，在目标满足稀疏性的前提时，可通过有限的低维观测数据恢复高分辨的高维信号[6,7]。其中一类经典的信号恢复算法为贪婪算法，该类算法主要利用最小均方误差的思想，通过人为设置阈值，在每个迭代步骤中选择局部最优解，并在算法收敛后获得全局最优稀疏解。文献[8]将贪婪算法应用于稀疏信号恢复，从理论方面验证了此类方法的适用性。尽管该类算法复杂程度较低，运算速度快，但人为设置阈值的方式并不总能保证算法收敛后的解为最优稀疏解，有时只是局部最优，计算结果稳定性欠佳。

另一类稀疏恢复算法为凸优化类算法，该类算法是通过利用优化策略对稀疏信号进行有效恢复，主要解决关于目标的 ℓ0范数最优化问题。已有数学推导证明ℓ0范数优化问题为非确定性问题(Non-deterministic Problem, NP)[9]，可用最小化ℓ1范数方法进行近似计算， ℓ1范数可认为是最紧致的近似稀疏求解算法。典型的优化类算法包括凸优化(Con-VeX, CVX)[10]和迭代软阈值算法[11]等，其中CVX算法基于不断的优化设计最终得到最优解，是一种标准的凸优化算法，在工程实验中应用广泛。但在高维数据情况下，典型的CVX算法面临着运行性能低，耗时过长的缺点。而迭代软阈值算法通过对目标函数进行近似替代，并将软阈值与优化策略相结合，提高了算法计算效率和收敛性能[11]，但由于迭代过程中需要手动调节迭代步长，算法自主学习程度不高。文献[12]将正则化范数与凸优化算法结合，用于SAR超分辨成像，证明了该类方法在效率和性能方面的优势，但繁琐的手动调整正则项系数步骤严重限制了该类算法在超分辨成像的精度及实用性。

还有一类稀疏信号恢复算法是贝叶斯类算法[13,14]，该类算法主要结合贝叶斯机器学习的思想对信号进行重建。典型的贝叶斯类算法包括变分贝叶斯(Variational Bayes, VB)推断算法和期望最大化(Expectation-Maximization, EM)算法等。文献[15]将贝叶斯机器学习结合应用于SAR地面动目标成像，选取拉普拉斯分布进行先验建模，利用VB-EM算法进行贝叶斯推理计算，并通过实测数据获得了高精度的恢复结果。贝叶斯类算法的优点在于建模过程应用灵活，而且能提供参数的区间估计。但传统基于贝叶斯机器学习的成像算法在贝叶斯推理过程中面临复杂的参数调整步骤和高维的矩阵逆运算的问题，计算效率较低。

基于以上分析，本文提出一种基于贝叶斯Lasso的稀疏ISAR超分辨成像算法，研究建立凸优化Lasso模型与贝叶斯概率模型之间的等价联系，解决凸优化稀疏算法中面临的繁琐手动调节正则项系数的问题。本文通过在分层贝叶斯框架下实现对稀疏Laplace先验的概率建模，同时考虑对优化过程中相应ℓ1范数正则项稀疏调节系数建立条件概率依赖模型，并利用马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)采样算法从数据中自动学习产生正则项系数，避免繁琐手动调节步骤，最终实现对目标超分辨ISAR成像的精确恢复。针对高维情况下超参数难以求解的问题，本文采用吉布斯(Gibbs)采样的方法对建模的参数进行统计采样估计。Gibbs采样方法是一种经典的MCMC算法，在统计机器学习方面应用广泛[16]。本文将贝叶斯Lasso模型与Gibbs采样方法结合，避免了复杂的参数调整步骤，实现了算法自动化程度提升，增强了稀疏恢复算法的稳健性，提高了算法实用性和恢复精度。本文实验部分应用多种ISAR仿真和实测数据，通过与稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)算法和CVX算法进行对比实验，从抑噪和超分辨性能等不同角度定性的分析了所提算法在性能上的优势，验证所提算法在ISAR图像恢复方面的高精度性和实用性。

2 回波信号模型

ISAR成像过程中，雷达保持静止状态，非合作目标通过相对运动形成虚拟孔径。根据ISAR成像原理可将目标相对雷达视线方向的运动分为平动和转动，其中平动会造成成像时目标散焦，需要进行平动补偿，转动提供了方位向分辨率，是成像过程中需要利用的关键部分。经过包络对齐和相位自校准后，ISAR成像可等效为转台几何模型如图1所示，其中目标飞机从A位置运动到B位置。在目标运动过程中，目标观测角发生变化，用 θ(t)表示，其中 t为慢时间。坐标系的原点O与目标中心重合，Y轴与雷达观测目标视线一致，X轴与Y轴垂直，雷达与目标中心点之间的距离以R (t)表示，初始距离设为 R0，则目标散射点与雷达之间的距离可表示为

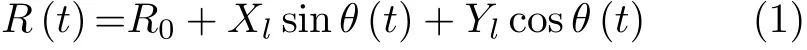
其中( Xl,Yl)为目标散射点的位置坐标。

当CPI较大时，ISAR成像分辨率高，但由于高阶运动分量的影响，目标运动复杂多变，处于非匀速运动状态，使得在长CPI内对ISAR的成像分析面临很大的困难。当CPI较小时，ISAR成像积累时间短，目标可认为处于匀速运动状态，目标运动状态简单，因此成像过程易于分析。但由于CPI小时，雷达接收回波数量过少，会造成成像分辨率低，难以满足ISAR超分辨的需求。针对此问题，本文利用压缩感知理论，在有限CPI内进行稀疏成像，实现ISAR超分辨，保证最终成像分辨率[17,18]。在CPI较小时雷达观测角可表示为θ (t)=ωt，其中ω为雷达转动角速度。由于有限CPI内雷达回波积累时间相对较短，此时式(1)可进一步表示为

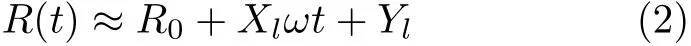
图1 ISAR成像示意图

3 贝叶斯Lasso

观察如式(4)所示的ISAR信号模型，目标成像问题可以解释为关于散射场 X的线性方程组求解问题。由于ISAR接收回波有时是不完整的，在强噪声和干扰情况下关于目标 X的线性方程组求解的数学模型一般是非齐次欠定的，进而造成了解的非唯一性和计算复杂性。针对这个问题，可利用压缩感知技术提供解决途径，在稀疏先验假设条件下，将非齐次欠定线性方程组的求解转变为对Lasso问题进行求解，数学模型如式(6)所示

为得到散射场 X的后验概率分布，需要选取符合目标特征的先验分布。由于ISAR目标具有稀疏性的特点，本文利用拉普拉斯先验分布对目标场景进行先验建模。拉普拉斯分布具有良好的重尾特性，可以有效地模拟目标的稀疏特征[7]。但由于拉普拉斯先验分布与式(7)的高斯似然函数不共轭，因此无法直接计算后验分布的闭合解析解。针对这个问题，本文采用层级(hierarchical)贝叶斯模型对先验进行概率建模，通过引入超参数构建层级之间变量的紧密联系，进而实现ISAR成像目标 X的有效估计计算。

由于ISAR成像回波数据为复数形式，本文在分层模型的第1步将 X 建模成依赖于超参数α 的复高斯分布，建模过程如式(8)所示

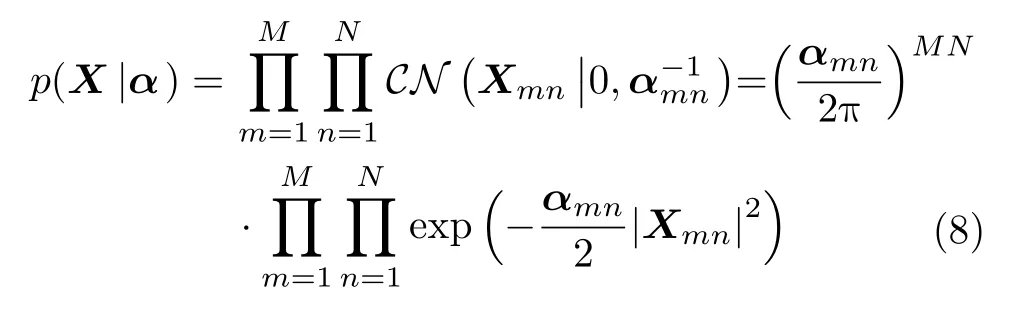
其中 α表示方差倒数矩阵，且α 的第m n个元素αmn>0。由于高斯函数固有的平滑特性，式(8)不属于稀疏分布范畴。为促进先验的稀疏特性并简化后验分布的推导，本文选取与高斯分布成对共轭的伽马(Gamma)分布作为超参数α 的先验，并在分层模型的第2步将超参数α 建模成如式(9)的形式

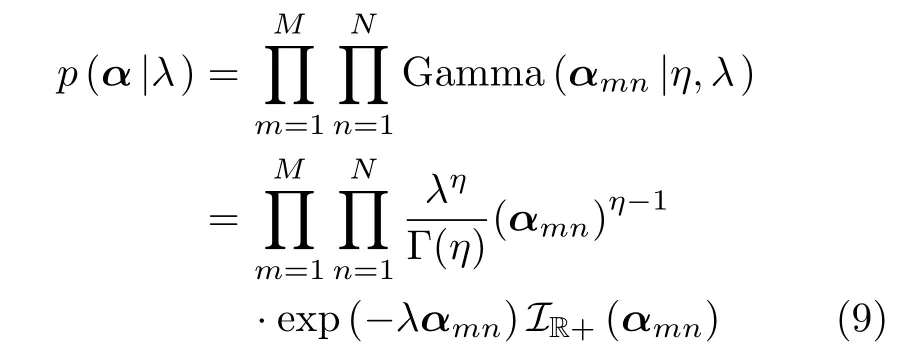
为提高ISAR成像精度和分辨率，并实现参数的自动调整，本文通过对正则化系数 λ设定一个先验分布并进行分层贝叶斯建模，将惩罚项系数 λ作为超参数引入分层贝叶斯中。同时求取 λ相应的后验概率密度分布，进而将惩罚系数与后验概率密度分布相联系，实现参数自主学习。为减少外界人为因素的影响，本文将 λ的先验建模为Gamma分布，概率模型如式(10)所示

图2 贝叶斯层级模型(有向无环图，DAG)

上述贝叶斯分层中参数与超参数的关系可用有向无环图(DAG)进行表示，对应贝叶斯模型如图2所示。其中 Y 表示ISAR接收回波数据， X为待恢复的成像目标， α和λ 为引入的超参数。 X和α 的紧密结合能够促进先验的稀疏性，而对 λ的概率建模则将正则项系数引入层级模型，为参数自学习提供了条件，虚线方框中的a, b, c, d 和η 均为固定参数。

常见文献中对式(12)后验分布的求解方法可分为两种，一种是利用VB的方法进行近似求解，另外一种是利用基于统计采样的MCMC采样方法进行估计计算。在高维情况下，采用VB的方法进行后验求解面临繁杂的参数调整和矩阵逆运算，算法自学习能力不强，需要人工手动介入，计算效率较低。而MCMC统计采样方法依赖马尔科夫链进行递归采样，在进行贝叶斯推理的过程依赖各参数的条件后验概率分布，是一个数据驱动的过程，无需过多的参数调整步骤，在算法自学习方面具有很大的优势。为提高算法性能和成像精度，减少复杂的人为介入参数调整，本文在贝叶斯层级模型下建立各参数依存的概率分布关系，并利用经典的Gibbs采样算法进行后验概率估计，最终达到对目标散射场 X的高精度恢复。

4 Gibbs采样算法

Gibbs采样算法是MCMC方法中一种经典的采样方式，其以变量的后验概率分布为基础，构造具有马尔可夫统计特性的转移矩阵，并以转移矩阵为采样核构建采样链，进而对变量及其统计特征进行采样估计。Gibbs采样算法通过将高维度计算问题进行分解，转换为低维度问题进行运算，并且能够对随机采样样本充分保留，具有高接受率。因此本文利用Gibbs采样算法对所提出的贝叶斯Lasso层级模型中的变量和超参数进行统计采样计算，并对参数依赖的后验分布进行估计，实现对待恢复目标的高精度求解。

在应用Gibbs采样算法进行采样计算之前，需要对各参数服从的后验概率密度分布进行推导。首先根据式(11)中噪声精度 β的先验分布与式(7)中的似然函数可得精度β 的后验分布如式(15)所示

由于采样算法的马尔可夫链需要一定的迭代次数才能达到收敛状态，收敛后最终得到的样本就是服从后验概率分布的样本估计值，而收敛之前的迭代过程称为老化期(burn-in period)。处于老化期的采样结果具有较大的误差，在进行估算过程中需对这部分数据进行舍弃。表1中步骤(2)设置了老化期门限 T，经过一定的迭代后由Gibbs采样器得到的样本逐渐收敛到目标分布，此后由采样得到的样本可用于参数和变量的估计计算。为降低误差的影响，对收敛后的采样样本进行均值求解可得出最终X的采样估计值，即为待恢复的ISAR成像目标散射 场 X。

表1 贝叶斯Lasso算法流程

5 实验验证

5.1 仿真数据验证

为进一步验证贝叶斯Lasso算法的优越性和通用性，本文利用仿真数据Mig-25对所提模型及算法的成像性能进行验证。通过在不同降采样率和信噪比下对目标场景进行恢复重建，并与由距离多普勒(Range-Doppler, RD), CVX和SBL算法得到的成像结果进行对比，从而验证所提算法的优越性和稳健性。图3给出了信噪比为5 dB降采样率变化时，通过不同方法所得的实验结果。其中图3第1列和第2列分别表示降采样率为0.25和未进行降采样时分别利用RD, SBL, CVX和本文贝叶斯Lasso算法进行处理后的恢复结果。从图3中可以看出利用RD方法进行成像时，成像结果背景噪声大，目标不明显。而SBL, CVX和贝叶斯Lasso 3种算法则实现了对噪声的抑制，以及对成像效果的增强，其中又以贝叶斯Lasso算法的效果最好，从而证明了本文贝叶斯Lasso算法的实用性。

图3 信噪比5 dB不同降采样率成像结果

为验证本文贝叶斯Lasso算法在抑噪方面的优越性能，图4给出了降采样率为0.5条件下信噪比变化时通过不同算法恢复的结果。其中图4第1列和第2列分别表示信噪比为0 dB和信噪比为5 dB时分别利用RD, SBL ,CVX和该文贝叶斯Lasso算法恢复的成像结果。从图4中可以看出RD重建的结果背景噪声很大，目标不明显，利用SBL和CVX算法恢复的图像虽然有部分抑噪效果，但目标丢失了多数特征。与这3种算法相比，采用该文贝叶斯Lasso算法恢复的目标散射场飞机轮廓特征突出，背景噪声消除干净，性能最优。

5.2 实测数据验证

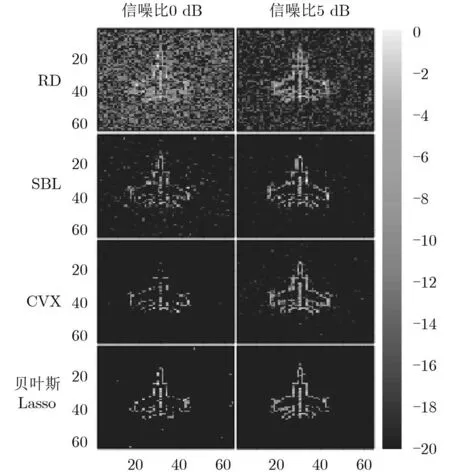
图4 降采样率0.5不同信噪比成像结果

图5 信噪比5 dB不同降采样率成像结果

实测部分采用Yak-42数据[12]进行实验分析，图5给出了信噪比5 dB条件下降采样率分别为0.25和未降采样的恢复结果。从图5中可以看出随着采样率的降低，RD恢复的目标淹没在噪声下，SBL算法恢复的结果目标丢失部分特征，CVX算法对噪声的抑制较弱，恢复的目标背景噪声斑点较多。而本文贝叶斯Lasso算法在低降采样率下保留目标大部分特征的同时，对噪声也起到了很好的抑制作用，总体性能优于SBL和CVX算法。

为验证本文贝叶斯Lasso算法在抑噪方面的优势，图6给出了降采样为0.5信噪比分别为0 dB和5 dB时不同算法重建的结果。其中在信噪比为0 dB时，RD算法得到的结果目标基本识别不清，并且背景噪声很大，SBL恢复的目标丢失大部分特征，并且机头部分基本无法识别，而CVX算法抑噪能力不足。从图6中可以看出，本文采用的贝叶斯Lasso算法在抑制噪声的同时保留了目标的多数特征，对目标进行了有效恢复，整体性能明显优于其他3种算法。

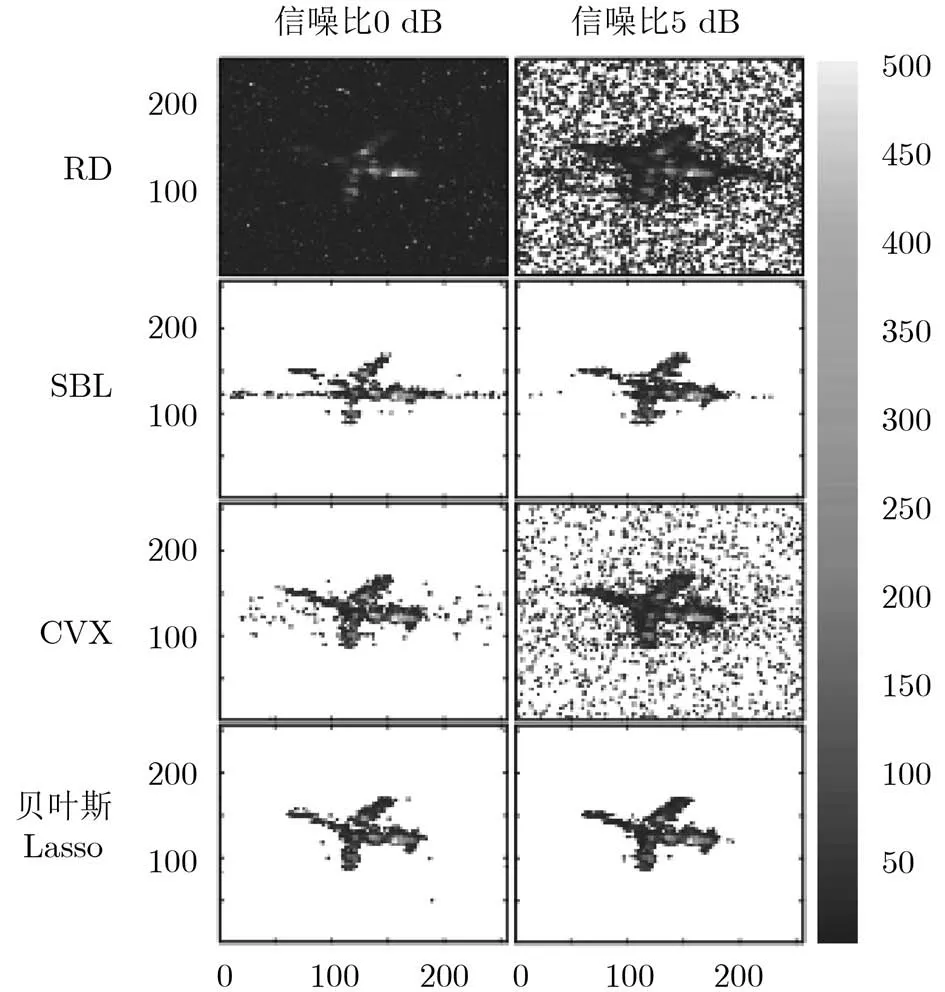
图6 降采样0.5不同信噪比成像结果

5.3 地面动目标实验验证

本部分通过对地面动目标进行成像分析，验证贝叶斯Lasso算法在实测数据的性能优势。地面动目标成像实验采用Gotcha-GMTI数据集[21]，该数据集由美国空军实验室发布，经由三通道机载雷达获取，雷达工作于X波段，作用距离10 km，发射信号带宽约640 MHz, PRF约2100 Hz。由于在对地面动目标进行成像过程中目标的运动特性会引起成像的偏移与散焦，本文利用杂波相消并采用吕氏变换方法(LV’s Distribution, LVD)[22]对调频发射信号中的多普勒频率和线性调频率进行协同估计，以改善动目标成像的聚焦和抑噪性能，提高成像分辨率。

图7(a)给出了采用RD变换后的参考成像，由图可见背景噪声抑制效果不明显。图7(b)、图7(c)分别为利用CVX和SBL算法的成像结果，从图中可以看出两种算法在抑噪方面均起到一定作用，但由于CVX算法难以适应不同距离单元的不同稀疏度，在成像过程中失去了部分目标特征，而SBL算法求解精度有限，目标恢复的效果不佳。图7(d)为采用本文贝叶斯Lasso算法得到的成像结果，与其他3种算法相比，由于贝叶斯Lasso算法无需人工干预参数选择，能够自主地适应空变的稀疏度，因此得到的成像结果信噪比更高，目标散射特征更清晰，从而验证了本文贝叶斯Lasso算法在成像性能方面的优越性。

5.4 相变图实验分析

为了定性验证本文贝叶斯Lasso算法性能的优越性，本文利用Donoho等人[23]提出的相位变化图(Phase Transition Diagram, PTD)进行实验分析。PTD是对算法精确性和稳定性进行评估的一种经典方式，其通过多次蒙特卡洛独立重复实验，获得恢复图像与参考图像相关量的平均值，并利用均方误差比较确定算法恢复的准确率，从而对算法的恢复精度进行定性分析。PTD将相变区域分为不可重建和可重建区域，并利用不同区域对算法的恢复性能进行直观的描述。本文在对算法进行评估分析时，通过100次蒙特卡洛实验得到重建图像与目标图像的平均相关值，并利用归一化均方误差(Normalized Mean Square Error, NMSE)进行判别图像恢复的准确率，NMSE的表达式为

图7 地面动目标成像

其中 Xk代表第k 次蒙特卡洛实验所得的恢复结果，X表示参考目标图像，阈值设定为0.0001，当NMSE<0.0001时认为图像重建成功。

图8 为利用相变图对S B L,C V X 和贝叶斯Lasso算法进行相变分析所得的结果。图8中各子图的右上方区域代表可重建区域，左下方区域代表不可重建区域。从图8中可以看出利用贝叶斯Lasso算法得到的相变图可重建区域要明显大于利用SBL算法得到的结果，并且与CVX得到的相变图非常接近，从而可以得出本文贝叶斯Lasso算法对目标的成像恢复能力要明显优于SBL算法，并且能够达到与CVX标准相近的性能。尽管CVX算法损耗大，运算时间长，并且高维情况下算法实用性不高，但由于CVX是一种标准的凸优化恢复算法，其可作为衡量其他算法性能优劣的参考方法。从图8(b)和图8(c)中可以看出由贝叶斯Lasso算法和CVX算法得到可重建区域非常接近，表明两者在算法恢复性能方面具有很高的相似度，从而验证了贝叶斯Lasso算法的优越性。

图8 相变图

6 结束语

本文针对凸优化ISAR成像算法繁琐的参数调整过程，研究建立凸优化Lasso模型与贝叶斯概率模型之间的联系。通过结合贝叶斯理论，建立贝叶斯Lasso模型，并采用分层方法对参数建立依赖的概率分布关系，在求取条件后验分布的同时利用Gibbs采样算法进行参数后验估计，实现了ISAR目标高分辨成像。实验利用相变图进行定性比较分析，并利用仿真和实测数据进行算法性能验证，证明了本文采用的贝叶斯Lasso算法的有效性和优越性。但是，在研究过程中，笔者发现标量正则项系数不能很好地模拟目标场景，有必要研究矩阵化的正则项，并实现矩阵正则项系数的自动调整，这将是后续工作研究的重点。