一种联合InISAR成像和微多普勒特征提取的空间目标转动矢量估计方法

2021-04-06朱岱寅

电子与信息学报 2021年3期

宫蕊汪玲徐楚朱岱寅

(南京航空航天大学雷达成像与微波光子技术教育部重点实验室南京 210016)

1 引言

在轨空间目标会由于燃料有限、设备陈旧或模块故障而被迫停止运转，在轨服务与维修工作能够有效地延长在轨工作系统的使用寿命，为进行长期频繁的空间活动提供强有力的后勤保障。随着国际范围内太空活动的频繁和卫星部署的数量与速度急剧增加，开展空间在轨服务以提升空间系统维护能力已经刻不容缓。

在轨服务主要有在轨卫星维护、轨道保护两种类型，其中在轨卫星维护主要工作是检测、维修以及寿命延长；轨道保护的目的是清除轨道垃圾，保持轨道的安全性[1,2]。在轨服务涉及与空间非合作目标的交会，或进一步的对接，而故障卫星因其姿控能力下降处于旋转状态，且无法提供转动矢量大小及方向信息，直接对接易造成对目标的额外损伤。轨道垃圾如空间碎片等也普遍处于高速自旋运动状态，直接抓捕具有较高的危险性。因此，获取非合作目标的转动矢量信息，以及外形、关键部件的位置信息是实现非合作运动目标自主会合、成功实施在轨服务的一项挑战。

传统逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)用于获取非合作运动目标的2维高分辨率图像，是用于识别非合作运动目标有效的手段[3,4]。但ISAR获得的2维图像是3维空间目标在距离-多普勒平面上的投影，ISAR成像投影面与目标相对于雷达的转动相关，因此2维图像会随时间的变化存在明显差异，无法对目标实际外形特征和尺寸进行判别。与传统ISAR 2维成像相比，干涉逆合成孔径雷达(Interferometric ISAR, InISAR)3维成像技术可以获取目标的3维空间分布，反映目标的真实尺寸以及结构信息[5,6]，在此基础上，进一步进行目标的转轴方向和旋转周期估计，提供目标的精准运动状态，从而解决当下面临的非合作运动目标自主会合和对接难题。

文献[7]利用InISAR系统获得非合作目标有效转动矢量的估计，但是无法估计目标总转动矢量在雷达视线方向(Line Of Sight，LOS)的值。文献[8]利用局部多项式傅里叶变换(Local Polynomial Fourier Transform, LPFT)提取雷达回波中的高阶分量，进而估计目标转动矢量在雷达LOS方向上的分量。由于雷达回波中的高阶分量很小，这种估计方法具有较大的估计误差。文献[9]采用MIMO雷达体制，将重建目标3维图像上散射点进行分组，利用主成分分析(Principal Component Analysis,PCA)的方法估计目标总的转动矢量方向，该方法最大的难点在于对散射点进行分组。

结合InISAR 3维成像技术及微多普勒特征提取技术，本文提出了一种新的空间非合作目标转动矢量估计方法。首先对“L型”三天线InISAR系统接收到的回波分别进行脉冲压缩、运动补偿、相位配准和方位向快速傅里叶变换(Fast Fourier Transform, FFT)处理，得到3幅ISAR高分辨2维图像。通过图像两两共轭相乘获取干涉相位信息，进而联合方位向峰值点信息估计有效转动矢量，同时得到目标散射点方位向与高度向位置信息完成3维成像。在此过程中，针对强散射点周边布满虚假散射点出现散射点簇的问题，使用多通道“CLEAN”技术来提取强散射点，使成像结果更加清晰，提高3维成像质量。在获得目标有效转动矢量的基础上，利用微多普勒特征提取的方法估计非合作目标总旋转速度，通过与有效转动矢量联合，获得目标的总转动矢量。

本文的结构安排如下：第2节详细给出InISAR 3维成像模型，包括系统几何模型、信号模型、相位配准、基于CLEAN法的峰值点提取和干涉过程。第3节给出非合作目标总转动矢量的估计方法，包括基于InISAR系统的有效转动矢量估计与基于微多普勒特征提取的总转速估计。第4节通过仿真实验验证方法的有效性。第5节总结全文并得出结论。

2 InISAR 3维成像模型

2.1 系统几何模型

本文采用“L型”三天线结构的InISAR 3维成像系统，成像系统几何模型如图1所示。雷达天线AC, AH, AV位于 Tξ坐标系中。其中，收发天线AC位于 Tξ坐标系原点O ，坐标为( 0,0,0), ξ2轴为雷达视线方向。接收天线AH位于 Tξ坐标系水平方向ξ1轴上，坐标为( dH,0,0), dH表示水平基线长度。接收天线AV位于 Tξ坐标系竖直方向ξ3轴上，坐标为(0,0,dV), dV表示竖直基线长度。dH和dV两基线相互正交。

图1 “L型”三天线InISAR 3维成像系统

非合作空间目标位于Tx坐标系中，目标中心位于坐标系原点 O ，Tx坐标系原点o 位于Tξ坐标系的坐标为 (0,R0,0)。其中，x2轴与雷达视线方向ξ2重合。在 Tx坐标系中，目标任意散射点xi的坐标为(x1,x2,x3) 。将目标总转动矢量 Ω投影到平面(ξ1,ξ3) 上的有效转动矢量Ωe定义为x3轴。平面(x1,x3)垂直于雷达视线方向。平面( x1,x2)为成像投影面与有效转动矢量 Ωe垂直。φ 表示有效转动矢量的方向，同时也确定成像投影平面的方向。由于参考系 Tx随时间变化，我们定义初始时刻参考系为Ty，任意散射点坐标由Ty变换为Tx的旋转矩阵由Myx表示

2.2 信号模型

空间非合作目标近似为散射点模型，假设目标包含 K 个散射点，σi为散射点i (x1,x2,x3)的散射系数，以收发天线AC为例，接收宽带线性调频信号(Linear Frequency Modulated, LFM)回波为

泰勒展开后，散射体的位置矢量表示为

对于线性调频信号的处理，使用解线性调频(dechirp)进行脉冲压缩，运算简单并且能够简化设备，广泛运用于ISAR回波的接收处理中。天线(AC, AH或AV)接收散射点i (x1,x2,x3)的回波信号经过解线性调频处理以及去剩余视频相位(RVP)后，可以表示为

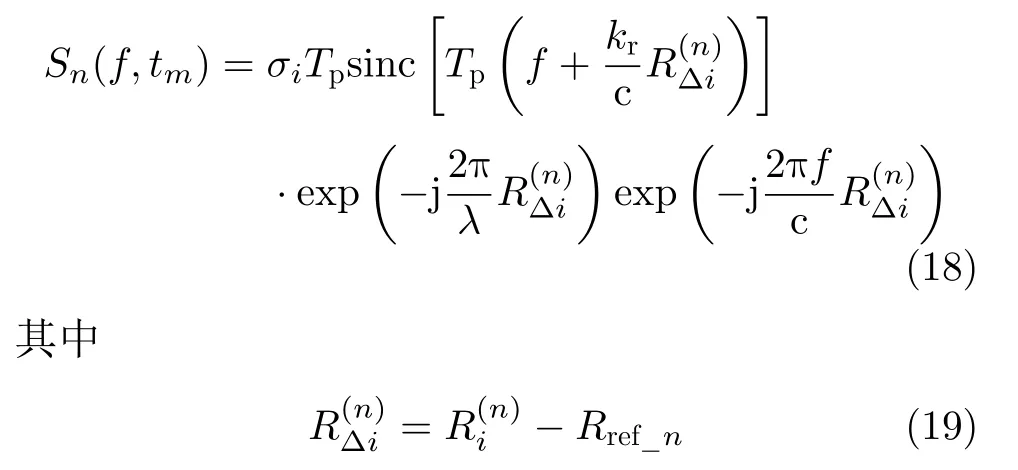
Rref_n为dechirp处理去差频过程中选取的参考距离，具体表达式将在2.3节进行推导。

2.3 相位配准

若采用传统方法即用中心天线估计的相同运动参数对各个天线进行统一补偿，即Rref_AC=Rref_AH=Rref_AV=R0，那么图像在方位维上将导致失配。为了使相同散射点对应相同像素点，对不同天线回波分别采用各自的参考距离进行补偿

其中， o(tm)为Tx坐标系原点O 的坐标(0,R0,0)，内积展开后有

将式(19)–式(25)代入式(18)中，并对慢时间tm进行傅里叶变换，得到天线AC接收到的回波信号复数域上的ISAR 2维图像为

2.4 CLEAN法

与方位时间相关的2次项的存在，导致简单距离-多普勒方法生成的图像在方位维度上散焦，成像质量下降。由于ISAR图像的散焦问题，会在ISAR 像的真实散射中心附近出现一些“虚假点”，距离真实散射中心最近的“虚假点”的散射强度往往与真实值量级相当，因而进行峰值提取时很容易作为强散射点被提取出来。此时得到的InISAR 3维成像结果就会出现大量“散射点簇”，在一定程度上降低了3维成像质量。为了解决这个问题，本文利用CLEAN技术结合峰值检测，保留峰值点。借助CLEAN技术，剔除冗余的虚假散射点，最终可以从散焦的ISAR图像中获得清晰的ISAR像，解决了因散焦造成3维成像时出现虚假散射点簇问题。用于后续干涉处理得到的3维成像与转动矢量估计结果将更加清晰并接近目标真实模型。

在保证精度的情况下尽量减少工作量，本文采取只搜索和提取AC通道上的2维ISAR图像中的峰值位置矩阵，用峰值所在位置矩阵提取配准后天线AH和天线AV图像对应点。

2.5 干涉3维成像

由于已经经过有效配准，采用联合搜索可以有效降低运算量[10]，即用CLEAN技术得到的峰值位置矩阵P [mri,mai]分别对天线AH和AV的图像提取对应点进行干涉处理，由式(26)，式(27)，得散射点i处的正交基线上两雷达回波干涉相位差

3 总转动矢量估计

3.1 有效转动矢量估计

所以天线AC得到的ISAR图像方位向多普勒峰值为

3.2 总旋转周期估计

使用上述InISAR 3维成像系统可以获得非合目标有效转动矢量的估计，然而仍然缺失总转动矢量在雷达LOS方向上的估计值。雷达目标除质心平动以外的旋转和振动等微动会对信号产生频率调制，采用时频分析可以有效地提取由目标微小运动引起的微多普勒特征[10]。通过时频分析，将目标经历完整旋转周期的ISAR回波数据投影到时间-频率平面上，观察微多普勒频率随时间的变化周期从而获取非合作目标的旋转周期[11]。

由式(18)可以得到，天线AC得到的ISAR 1维距离像序列可以表示为

从式(41)可以看出，自旋目标1维距离像峰值的出现位置符合正弦变化，且变化周期与目标自旋周期相一致。因此，对于尺寸相对较大的目标，其散射点距离走动相对较大，可以通过观察目标距离像峰值的变化周期来估计目标旋转周期。

但是，通常情况下，ISAR目标相对较小。此时，目标上散射点距离走动仅仅跨过1个距离分辨单元甚至不超过1个距离分辨单元，目标1维距离像近似为一条直线[12–18]。提取目标距离像的第 k个距离单元，其关于慢时间tm的表达式为

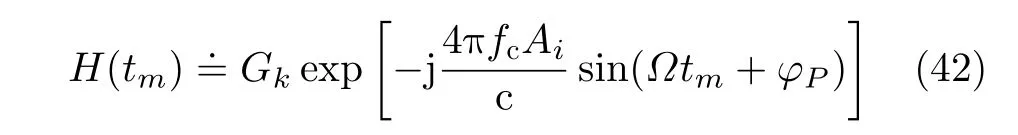
其中，Gk为一个常数。由式(42)可以得到，距离单元的慢时间序列相位项随时间正弦变化，变化周期与目标自旋周期相等。因此，即使目标的自旋微动幅度较小，从目标距离像峰值无法直接观测出变化规律，也可以利用时频分析的方法得出目标回波1维距离像的慢时间序列微多普勒频谱，获得目标转动周期估计值，通过式(43)得到目标转速估计

4 仿真数据处理验证

4.1 仿真参数

仿真卫星3维模型如图3所示，对模型进行简化，构造卫星散射点模型，如图4所示，模型尺寸为10 m×14 m，包含37个散射点，点间距1 m，仿真实验时假设每个散射点的散射系数相同。InISA R成像参数设置如表1所示。

4.2 仿真实验

使用如表1所示参数进行仿真。在整个仿真过程中，信噪比设置为15 dB，有效转动矢量方向角设置 φ=10◦=0.1745rad，总转动矢量设置为Ω =(0,0.03 rad/s,0.04 rad/s)。

成像结果如图5与图6所示，其中图5为天线AC经过脉冲压缩与运动补偿后ISAR 2维成像图，图6为经CLEAN法改进的成像结果。

从图5可以看出，由于与方位时间相关的2次项的存在，距离-多普勒方法生成的图像在方位维度上散焦，导致成像质量下降，直接3维成像会造成虚假散射点簇。图6经过CLEAN技术搜索并提取峰值，成功解决了因图5的散焦造成3维成像时出现虚假散射点簇问题。说明了CLEAN技术性能良好，可以获得清晰干净的2维图像，为InISAR 3维成像提供了条件。

图2 算法流程图

图3 卫星模型图

图4 卫星模型散射点3维图

卫星目标的3维成像结果图及对应3视图如图7所示，其中蓝色圆圈表示仿真卫星散射点的真实位置，红色*点表示目标3维成像的位置。卫星目标的完整旋转周期为157 s，图8为含有两个完整旋转周

表1 InISAR系统参数

图5 天线AC距离-多普勒(RD)2维成像结果

期的未补偿的SAR1维距离像序列。图9为第81个距离单元的微多普勒频谱。

从图7的3维图像结合3视图可以看出，InISAR 3维成像系统可以有效地重建出卫星目标的3维图像。将图8放大，可以观察到大致翻转周期信息。为了精确估计，采用时频分析获取微多普勒频

图6 天线AC使用CLEAN法的成像结果

谱的方式得到周期值。图9展示的微多普勒频谱是大量正弦调制的叠加，仍可以看出周期性。对图9进行了图像提取与曲线拟合得出目标转速估计值。

结合图7与表2可以看出，联合InISAR成像和微多普勒特征提取的空间目标转动矢量估计方法在3维成像和转动矢量估计方面都表现出了良好的性能，重建后与卫星散射点模型基本吻合，转动矢量估计误差微小。

为体现本方法的有效性，改变总转动矢量方向进行多组实验，2维CLEAN成像结果与3维成像结果如图10，图11，转动矢量估计与重建误差如表3。

表3直观地展示了：在多组试验下本文所述方法依然具有很小的3维成像误差以及总转动矢量估计误差。受到成像投影平面的限制，在一些成像几何中，2维成像时一些关键点没有被投影在IPP中，此时将无法将这些点提取出来，因此3维重建结果精确度略微下降，但仍然可以反映出目标的真实尺寸以及结构信息，总转动矢量估计误差也并未受到影响，验证了本方法的有效性。

图7 卫星目标3维成像结果图

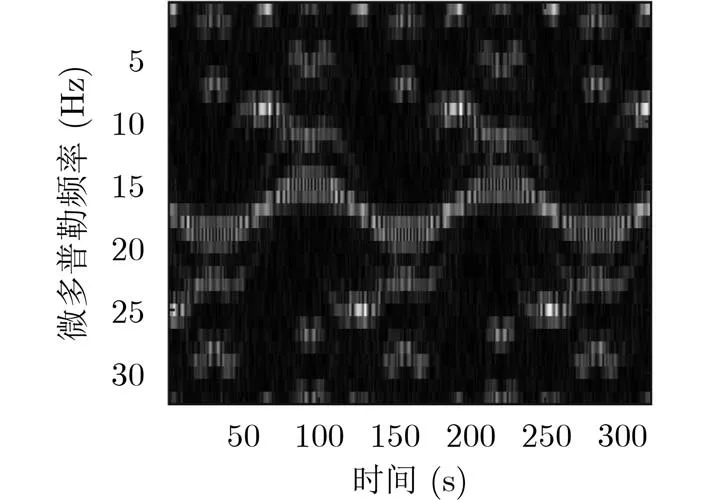
图8 卫星目标1维距离像序列

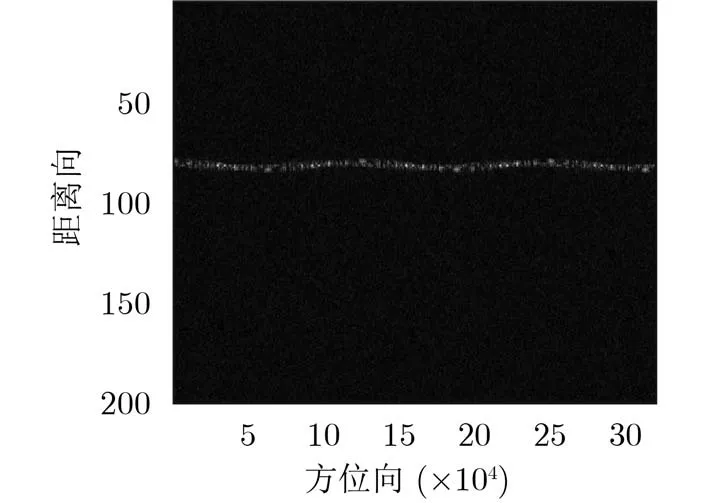
图9 卫星目标距离单元回波微多普勒频谱图

表2 重建误差

5 结论

空间目标转动矢量的准确估计是提供空间非合作运动目标的精准运动状态、安全实施在轨服务的基础。本文提出了一种新的空间非合作目标总转动矢量估计与3维成像方法。通过对距离-多普勒算法生成的2维ISAR图像使用CLEAN技术提取各散射点的峰值，并设计了联合搜索策略在提高计算效率的同时减小方位向散焦并得到清晰的像，对3幅ISAR图像使用InISAR技术获取不同天线与目标之间的波程差。在此基础上，估计出目标有效转动矢量并得到3维高分辨图像。进一步采用微多普勒频谱分析的方法得到目标总转速估计。最终得到目标的总转动矢量估计。对卫星目标仿真数据处理的结果表明，本文所述方法有较好的3维成像效果以及较小的总转动矢量估计误差。