基于子阵近场零陷权的联合波达方向估计方法

生雪莉 刘 婷 杨超然 郭龙祥 穆梦飞

(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

(海洋信息获取与安全重点实验室(哈尔滨工程大学)工业和信息化部 哈尔滨 150001)

(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

远距离波达方向 (Direction of Arrival, DoA)估计是水下目标检测领域的研究热点之一，并在雷达、导航、无线通信等其他领域[1–3]有着广泛的应用。目标位于远场，即目标与接收基阵之间的距离比阵列孔径大得多时，信号以平面波的形式入射。传统的常规波束形成 (Conventional Beam Forming, CBF)[4]是一种常用的阵列信号处理方法，该方法根据目标信号的来向对各阵元接收到的信号进行延时补偿求和，当扫描角度与目标方位一致时，可实现抑制噪声、增强目标信号的效果，从而正确估计目标方位。CBF的优点是仅需少量样本即可得到较为可靠的DoA估计结果，但其空间谱的主瓣较宽、旁瓣较高，角度分辨力较差。为解决此问题，最小方差无畸变响应 (Minimum Variance Distortionless Response, MVDR)[5]算法、多重信号分类(MUltiple SIgnal Classification, MUSIC)[6,7]算法和借助旋转不变技术估计信号参数 (Estimating Signal Parameters via Rotational Invariance Techniques,ESPRIT)[8]算法应运而生。但由于存在空间非均匀噪声和近场强干扰，这些算法大多已不再适用，空间非均匀噪声会提高这些算法的空间谱背景级，同时近场强干扰会覆盖真实目标信号。

常用的抑制近场干扰的方法有两种：一种是矩阵空域预滤波[9,10]，另一种是设计近场零陷权[11]。由于前者计算量大、实时性差，本文选择了第2种方法。实际上，海洋环境噪声在空间上是不均匀的。Moghaddamjoo[12]假设各个阵元处的白噪声是非均匀的、不相关的，这意味着噪声协方差矩阵是一个对角矩阵，其对角线上的元素代表未知且不相等的噪声功率。在此条件下，使用传统的波束形成方法估计目标方位时，往往需要提前估计噪声协方差矩阵[13]，然后进行预白化数据相关矩阵处理[14]，计算复杂度较高，限制了其实际应用。因此，如何解决长线阵在近场强干扰及空间非均匀噪声下的远距离目标方位估计问题是水声阵列信号处理领域的研究热点之一。

本文基于长线阵的特性，提出了一种基于长线阵分子阵近场零陷权的联合目标方位估计方法。本方法将长线阵划分为高重叠子阵，一方面减轻阵列大孔径对信号相关性的影响，另一方面充分利用阵元接收数据。同时以子阵为单位设计近场零陷权来抑制近场辐射声干扰，再基于各子阵对远场目标DoA估计结果几乎一致的特点，利用空间频率方差的倒数加权综合各子阵DoA空间谱，从而达到抑制非均匀噪声、降低空间谱背景级、提高输出信噪比的目的，最终实现远场目标方位的准确估计。

2 基于近场零陷权的干扰抑制技术

海底长线阵在近场辐射声干扰及空间水平非均匀噪声下探测远距离目标时，目标与干扰源几何位置关系如图1所示。

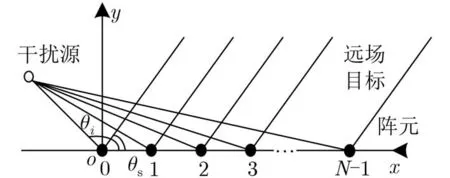
图1 干扰源、目标及阵列几何位置关系示意图

在实际远距离目标DoA问题中，信号多为宽带形式，常采用将宽带信号离散傅里叶变换 (Discrete Fourier Transform, DFT)在频域上分解为多个窄带信号的和，针对每个频率单元进行信号处理的方式。将各阵元接收宽带信号DFT

针对干扰源，参考近场聚焦波束形成方法可得频率fu处近场方向矢量a(ri,θi,fu)

此时，可得频率 fu处最优近场零陷权向量和最优近场零陷权向量下的空间谱为

其中， fl为处理频带的最低频率，fh为处理频带的最高频率。

此方法可以实现在远距离目标DoA过程中，抑制近场的干扰，较准确地估计出真实目标所在方向。可有效分离近场干扰和远场目标的关键前提为近、远场信号包含不同的频率成分，且差异性越大效果越好。但该方法要求阵元数目不能太多，干扰噪声为各向同性的高斯白噪声。

3 基于长线阵分子阵近场零陷权的联合DoA估计

长线阵经常用于水下远距离目标探测中，但阵的孔径过大会导致DoA中某些运算方法(典型为矩阵求逆运算)计算维度过高，使算法的实时性降低；也可能导致线阵上间隔较远的阵元的接收信号相关性变差，从而影响DoA估计结果。因此，本节将长线阵分解为重叠率较高的重叠子阵[15]，提出基于长线阵分子阵近场零陷权的联合DoA估计 (Subarray Joint DoA estimation based on Near-field Nulling weight,SJNN)。

3.1 基于子阵方位稳定性的方差加权技术

考虑信噪比足够大各子阵均可探测到目标的情况，由于目标位于远场，目标相对于各个子阵的方位角度相同。将长线阵分解为多个子阵，针对子阵，将其接收信号DFT后在频域上分解为多个窄带信号的和，以每个窄带信号为单位，求解空间谱，可得单频点子阵波束输出Rk(θ,fu)为 1 ×L的矩阵，其中 L为扫描角度个数，k =1,2,···,K , K为子阵总数； fu∈[fl,fh], fl为处理频带的最低频率，fh为处理频带的最高频率，u =1,2,···,F,F为频率单元总个数。针对每个子阵，将所有频率单元的子阵波束输出Rk(θ,fu)进行归一化处理。针对每个频率单元，记录每个波束输出最大值所在角度θk,fu，最大值所在角度对应着该频率单元的DoA估计结果。由于目标处于远场，每个子阵对目标所在角度的估值几乎相同，波束输出最大值所在角度是稳定的，而噪声对应频率波束输出最大值所在角度是随机的[16]。换句话说，针对每个频率单元，若存在所有子阵DoA估计结果几乎不变的情况，则说明目标信号包含该频率且DoA估计结果为目标方位；若子阵DoA估计结果相差较大，则说明此频率仅包含噪声(也可能包含能量较低的目标被随机检测，此类目标本文算法不可检测)，噪声对应空间谱幅度随机起伏。各子阵的目标方位角度估值为[θ1,fu,θ2,fu,···,θK,fu] ，定义空间频率ηk,fu=fucos θk,fu/c，统计空间频率估值[ η1,fu,η2,fu,···,ηK,fu]的 方差为δfu，其中噪声对应频率方差较大，而目标对应频率方差较小。在每个子阵DoA所得角度θk,fu的对应波束输出值上乘以方差的倒数，即

方差加权采用乘空间频率方差倒数的形式，子阵归一化波束输出取值范围为[0, 1]，空间频率取值范围为[–fu/c, fu/c]，其方差最小值设置为10–7，乘法加权保证方差倒数较小的情况下也可实现有效加权。由于测角和空间频率为非线性关系，目标越偏离阵列法线方向其测角误差越大，采用空间频率作为统计量对不同来向的目标更有意义。

进一步地，考虑目标方位估计结果具有固有闪烁、跳变等现象时，方差会变大，上述算法性能变差，甚至无法实现输出信噪比的提高，本文根据接收信号的线谱稳定性，将各频率对应的方差由小到大排列，对应线谱数目的方差(即线谱所在频率对应的方差)置零处理，从而提高该算法的适用性。

子阵包含阵元数越多，其本身的指向性指数越大，相应的检测目标能力越强，但相应的子阵个数会变少，会导致噪声对应空间谱最大值随机性不明显，对应的方差也可能较小，表现在空间谱上除目标所在方位外还存在其他伪峰。因此，子阵的划分在背景级抑制和检测能力上存在矛盾关系。子阵阵元个数占整个阵列的1/4～3/4时，噪声子空间维数下降，计算量减小，子阵非均匀信噪比变化范围减小，本文方法效果较好，且1/2时效果最佳，子阵噪声子空间维数约变为整个阵列的1/2，全面利用各阵元接收数据的同时有利于分离信号和噪声、加快运算速度。

结合该基于子阵方位稳定性的方差加权技术与近场零陷权技术，本文提出基于长线阵分子阵近场零陷权的联合DoA估计方法。在近场干扰可被抑制的前提下，针对该方法的波束输出在阵增益、主瓣宽度、平均背景级方面的特性，下面给出其与长线阵近场零陷常规波束形成方法的对比分析

式(10)为阵增益A Gθ的 计算公式，其中D (θ)表示指向性函数，即 P(θ)=D2(θ)。 假设将Q 元长线阵分成重叠子阵，每个子阵 N个阵元，每两子阵重叠 C个阵元。单个子阵较Q 元长线阵的指向性指数小10 lg(Q/N)。但本文方法通过方差加权综合各子阵的空间谱，可抑制非均匀噪声，其空间谱背景级会大幅降低，相应的阵增益有所提高，主瓣宽度有所下降。考虑目标由60 °入射，最低信噪比为–15 dB，信干比为–22 dB, Q=64, N =32, C =30的情况，本文方法与长线阵近场零陷常规波束形成相比平均背景级降低近60 dB，主瓣宽度约减小2 °，输出信噪比[4]改善量(定义为 SNRout=AGθ方法1−AGθ方法2)为13.3 dB。由此可见，本文方法虽然因子阵划分而降低了单个阵列的增益，但基于各子阵对远距离目标方位估计结果差异性小、非目标所在频率(噪声)对应空间谱最大值随机的特点，通过方差加权联合技术，增强了目标方向的波束输出能量，从而提高了阵列输出信噪比，带来较大的处理增益。

3.2 算法流程及具体步骤

基于长线阵分子阵近场零陷权的联合DoA估计算法流程图如图2。具体步骤为：

图2 基于长线阵分子阵近场零陷权的联合DoA估计算法流程图

(1) 将 Q 元长线阵分成重叠子阵，每个子阵N个阵元，每两子阵重叠C 个阵元，共有K 个子阵。

(2) 对每个子阵的各阵元接收信号作DFT，已知近场干扰坐标为( ri,θi)，每个子阵在每一个频率单元生成相应的近场零陷约束矩阵Bk(fu), k =1,2,···,K。

(3) 对每个子阵在每一个频率单元的接收数据同时进行近场零陷加权和频域波束形成，从而得到每一个频率单元的波束输出，记为Rk(θ,fu)。

(4) 针对每个频率单元，记录每个子阵波束输出最大值所在角度θk,fu。

(5) 在该频点处，统计各子阵的目标方位角度估值θ1,fu,θ2,fu,···,θK,fu，求其对应空间频率估值的方差δfu。

(6) 在每个子阵DoA所得角度θk,fu对应的归一化波束输出值上乘以方差倒数，将波束输出记为Dk(θ,fu)。

(7) 将各子阵处理后的波束输出值累和，各频率 单元结果累和，即为最终结果Dopt(θ)。

3.3 运算复杂度分析

对比长线阵近场零陷常规波束形成、长线阵近场零陷MUSIC以及本文研究的基于长线阵分子阵近场零陷权的联合DoA算法的运算复杂度，其差别主要集中在波束输出计算上，分别为O(FL(3Q2+Q)),O(FL(3Q2+Q+Q3)), O(FLK(3N2+N)+FK)。文中方法由于采用重叠子阵划分，复杂度略高于长线阵近场零陷常规波束形成，与长线阵近场零陷MUSIC方法相比不需要进行特征值分解因此复杂度较低，且本文方法复杂度可通过划分的子阵个数及子阵阵元数调整。

4 仿真分析

仿真采用64元直线阵(海试试验用阵)，阵元间距为目标信号最大线谱频率对应的半波长。接收信号时域快拍数为1000。近场干扰与直线阵第1阵元的水平、垂直距离均为4倍阵元间距。干扰信号为带宽为10～2000 Hz的干扰噪声，其中线谱频率为80 Hz, 100 Hz, 120 Hz。目标信号为带宽为10～2000 Hz的舰船辐射噪声，其中线谱频率为100 Hz, 150 Hz,200 Hz, 300 Hz。处理频带为100～400 Hz。

直线阵各阵元处的噪声能量级如图3所示。长线阵常规波束形成 (Conventional Beam Forming of Long Linear Array, LLA-CBF)方法定义为直接对64个阵元的接收信号(包含近场干扰信号和目标信号)进行常规宽带波束形成处理。长线阵近场零陷常规波束形成 (Near-field Nulling Conventional Beam Forming of Long Linear Array, NNLLA-CBF)方法是基于64元直线阵使用LLA-CBF算法前进行近场零陷处理[11]。长线阵近场零陷MUSIC (Near-field Nulling MUltiple SIgnal Classification of Long Linear Array, NNLLA- MUSIC)方法定义为基于64元直线阵进行近场零陷处理和宽带MUSIC波束形成处理[17]。子阵累和零陷常规波束形成 (Subarray Addition Nearfield Nulling Conventional Beam Forming, SANN-CBF)定义为将64元直线阵分解为17个32元重叠子阵，每个相邻子阵重叠30个阵元，针对每个子阵形成近场零陷、常规宽带波束形成处理再将各个子阵空间谱累和。

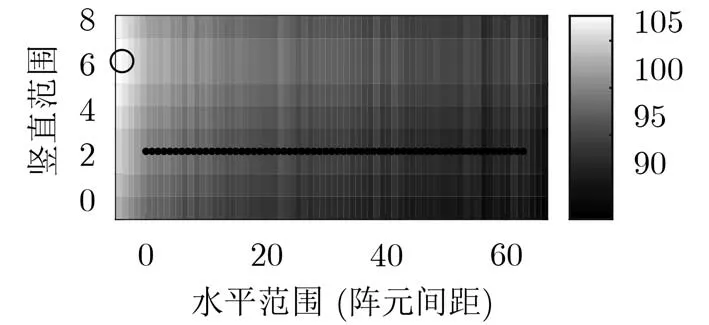
图3 各阵元处噪声能量级

仿真1 考虑目标由60 °入射，最低信噪比为–15 dB，信干比为–22 dB。图4为LLA-CBF, SANN-CBF,NNLLA-CBF, NNLLA-MUSIC以及本文研究的SJNN算法的空间谱对比图。由于近场干扰的存在，LLA-CBF只能显示近场干扰所在的大致方向，目标方位无法准确估计。针对长线阵使用零陷抑制技术，NNLLA-CBF能够有效抑制干扰，但由于噪声空间非均匀，其空间谱背景级较高，主瓣较宽、旁瓣较高且起伏大，估计精度较低。SANN-CBF能够有效抑制干扰，平滑旁瓣的起伏，但单个子阵阵元数目较少导致主瓣较宽旁瓣较高，估计精度不够理想。NNLLA-MUSIC算法由于频域单快拍且非均匀噪声的影响，虽然可在目标真实方位处形成峰值，但背景级很高，且零陷对干扰的抑制能力较弱。SJNN算法能够在子阵中抑制近场干扰，再通过方差加权，减少非均匀噪声的影响，有效地降低空间谱背景级，具有较高的估计精度。

阵元间距为300 Hz的半波长，信噪比较高时，300 Hz以上的目标连续谱成分会令子阵波束输出产生栅瓣，在实际噪声环境和近场零陷权的作用下，栅瓣可能高于主峰，导致最终的空间谱出现明显伪峰，且栅瓣通过频率累和可抑制但不可消除，而本文方法适用于低信噪比的情况，目标连续谱成分包含的能量过低，不能保证每个子阵都得到主瓣或者栅瓣的DoA估值，此时方差会较大，加权值不会很大，因此不会形成伪峰。实际中，零陷权矢量不仅与近场干扰所在位置有关，水声环境变化例如水声吸收、声速等因素对零陷权也会造成影响，且固定零陷权不适用于拖曳线阵，因此设置零陷权前需预先对水声环境、干扰源和阵列的几何位置关系进行测量，从而保证零陷权的环境适应性。仿真中远场目标信号采用舰船辐射噪声的形式(频谱中包含宽带连续谱和线谱)，本文方法对类似宽带信号，即包含多个频率信息的信号更加有效。

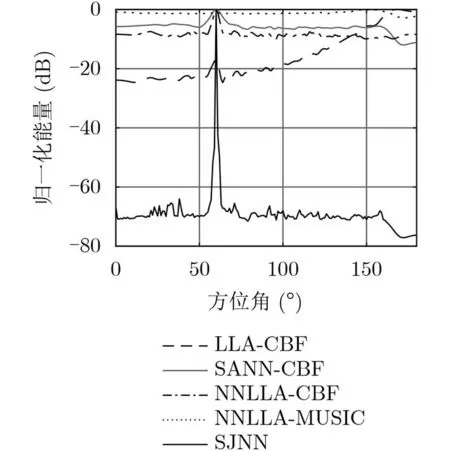
图4 单目标DoA估计空间谱

仿真2 考虑目标1由60°入射，目标2(240 Hz单频信号)由62°入射，最低信噪比均为–1 dB，信干比均为–12 dB。此时信噪比相对较高，从图5可看出LLA-CBF, SANN-CBF, NNLLAC B F 分辨力较差，无法区分间隔2°的目标。NNLLA-MUSIC算法可估计两目标所在角度，但其背景级较高且估计性能较差。在本文所采用的仿真条件下，SJNN算法可较高精度地估计不同频率目标所在方位。可有效分辨的条件为两目标包含不同的频率成分，即线谱频率不完全相同，且差异性越大效果越好。

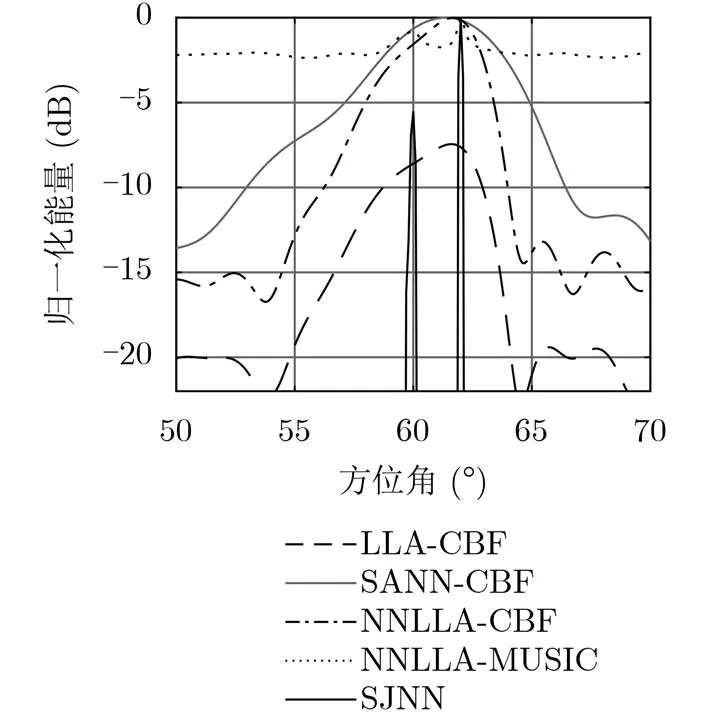
图5 多目标DoA估计空间谱

仿真3 对SANN-CBF, NNLLA-CBF,NNLLA-MUSIC, SJNN 4种方法的空间谱平均背景级进行比较，同时计算NNLLA-CBF与SJNN之间的输出信噪比改善量，非均匀噪声下的最低信噪比变化为–20～–2 dB。从图6可以看出，空间谱平均背景级随信噪比的增大而减小，NNLLA-MUSIC算法由于频域单快拍而背景级最高，SANNCBF由于多子阵的空间谱累加而背景级较高，NNLLA-CBF由于直接使用64阵元进行波束形成，其背景级较低。本文研究的SJNN算法在正确估计目标方位的前提下，空间谱背景级均在–60 dB以下，且目标方向能量较集中，空间谱目标峰值较尖锐，相比于NNLLA-CBF具有近15 dB的输出信噪比改善量(图7)，从而表明SJNN算法具有更好的提高信噪比能力和目标方位估计显示能力。

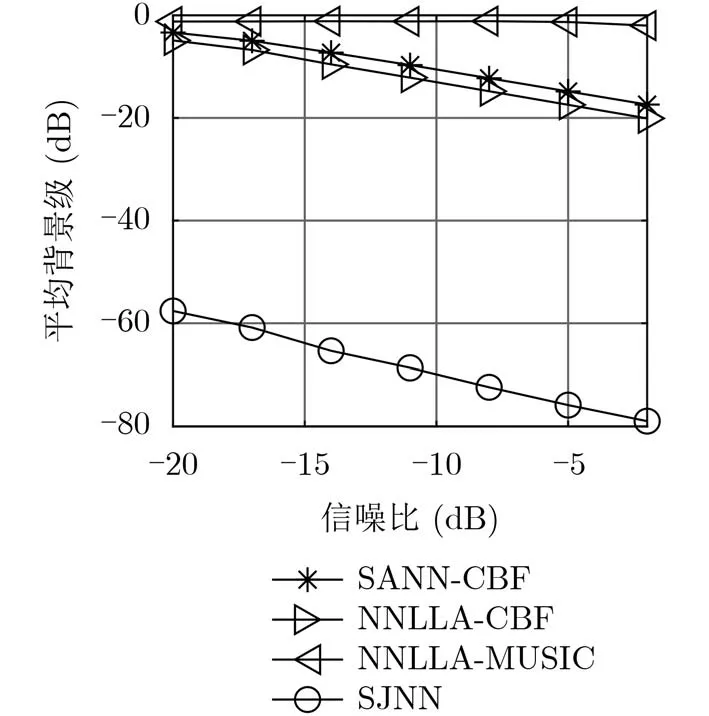
图6 平均背景级随信噪比变化曲线

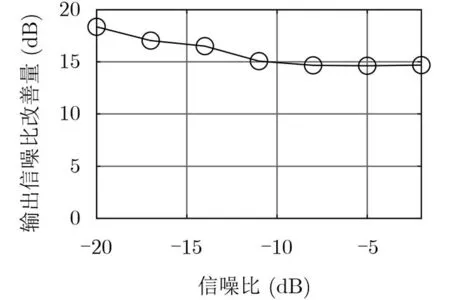
图7 输出信噪比改善量随信噪比变化曲线

仿真4 如图8所示，对SANN-CBF, NNLLACBF, NNLLA-MUSIC, SJNN 4种方法的均方根误差进行比较，非均匀噪声下的最低信噪比变化为–20～–2 dB。NNLLA-CBF与SJNN算法均在低信噪比下具有较小的估计均方根误差；SANN-CBF的均方根误差最大，尤其是在低信噪比条件下；NNLLA-MUSIC在较高信噪比条件下(最低信噪比为–2 dB)适用，且估计误差较大。SJNN算法的均方根误差稍差于NNLLA-CBF，因此本文算法以适当牺牲稳健性为代价来大幅度降低DoA估计的平均背景级，从而增强算法提高信噪比的能力。经仿真分析，该算法可适用的最低信噪比为–22 dB(0号阵元)，由于非均匀噪声的影响，63号阵元的信噪比为–13 dB，此时信干比为–29 dB。此外，随着信噪比的增加，4种算法DoA估计均方根误差均逐渐降低。

图8 估计均方根误差随信噪比变化曲线

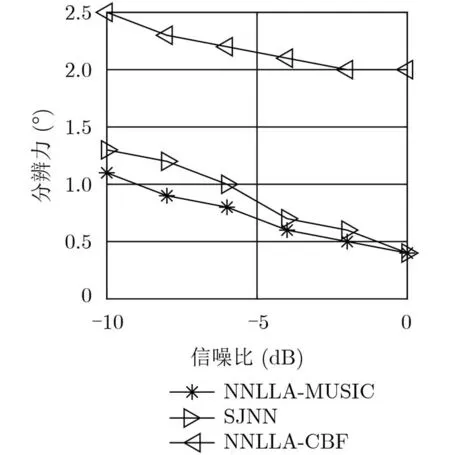
图9 角度分辨力随信噪比变化曲线

仿真5 如图9 所示，对N N L L A-C B F,NNLLA-MUSIC, SJNN 3种算法的角度分辨力进行比较，非均匀噪声下的最低信噪比变化为–10～0 dB。随着信噪比的增加，3种算法的角度分辨力均有所增强。其中，NNLLA-CBF算法的角度分辨力较差，该算法空间谱主瓣宽旁瓣高，可区分目标角度间隔在2°～2.5°。NNLLA-MUSIC, SJNN两种算法分辨力较好，且后者的空间谱背景级较低、主瓣相对较窄，因此理想条件下SJNN算法分辨力较前者更高，但本文算法多目标空间分辨能力与目标间的频谱差异、各频率的测角精度、连续谱高频成分的栅瓣影响等多种实际因素有关，实际中多目标空间谱的谱峰可能不会如图5般尖锐，空间分辨性能会有所下降。本文算法统计单个频率单元各个子阵的波束输出最大值对应角度并计算对应空间频率估值的方差，当多个目标包含不同的频率信息时，理想条件下会在这些频率处出现方差很小的情况，且波束输出最大值对应角度即为不同目标对应的不同方位，通过方差倒数加权即可增强不同频率对应目标的波束输出能量，再将各个频率单元的空间谱累和，因此在信噪比相对较高时不扩大整个阵列孔径即可提高空间分辨力。

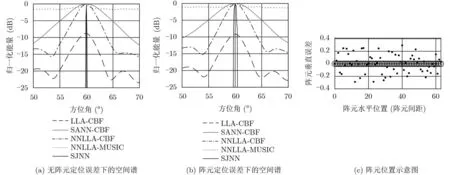
图10 阵元定位误差影响对比图

仿真6 如图10所示，针对SJNN算法，考虑阵元定位误差和近场干扰源定位误差的影响。目标由60°入射，最低信噪比为–5 dB，信干比为–12 dB。阵元定位误差定义为理想阵元位置“o”和实际阵元位置“·”之间存在一定的垂直随机距离，仿真中取值区间为(–0.3 d, 0.3 d)。真实阵元位置如图10(c)中“·”所示，图10(a)和图10(b)对比了有无阵元定位误差情况下的空间谱。在不考虑阵元定位误差的情况下，SANN-CBF, NNLLA-CBF,NNLLA-MUSIC以及本文研究的SJNN算法均可正确估计目标方位，LLA-CBF在目标方位也存在峰值，本文算法的空间谱主瓣最窄，背景级最低；考虑阵元定位误差的情况下，SANN-CBF, NNLLACBF, LLA-CBF空间谱形状几乎不变，说明这些算法对阵元位置误差的敏感性较低，比较稳定，而NNLLA-MUSIC以及SJNN算法虽然依旧可以估计目标方位，但主瓣均有所展宽；本文算法中各子阵对目标的方位估计结果存在一定误差，输出信噪比改善量减小了7.6 dB，甚至可能会在目标入射方向附近出现多峰值的情况。而相同情况下，仅考虑近场干扰源定位误差对算法空间谱的影响，理想近场干扰源位置为(–4d, 4d)，实际位置为(–5.05d,4.89d)，本文算法及其他对比算法的空间谱与不考虑近场干扰源定位误差情况下的空间谱几乎相同，只是在近场干扰方向略有起伏，因此，近场干扰源定位误差对本文算法影响较小，但会减弱算法对近场干扰的抑制能力。

5 结束语

在近场干扰、噪声非均匀的情况下进行远距离目标方位估计是水声探测领域的难点之一，近场辐射声会使目标信号淹没在干扰中，而非均匀噪声会提高DoA估计空间谱的背景级。本文提出基于长线阵分子阵近场零陷权的联合目标方位估计方法，将长线阵划分高重叠子阵，针对子阵生成近场零陷权来抑制近场干扰；利用子阵对目标方位估计结果的稳定性，方差加权综合各子阵空间谱，抑制非均匀噪声的影响。仿真结果表明，与传统的子阵累和零陷常规波束形成、长线阵近场零陷常规波束形成、长线阵近场零陷MUSIC相比，本文算法对应的空间谱具有更低的背景级，即更强的提高信噪比的能力，且在频域单快拍情况下具有更好的多目标分辨能力。需要指出的是考虑阵元位置误差的情况下，各子阵对目标方位的估计结果将存在一定误差，从而导致空间频率估值的方差变大，方法性能变差，因此如何提高算法在此条件下的性能还需进一步研究。