基于结构化思维的单元整合教学——以“除数是一位数的笔算除法”教学为例

□郑建锋 沈正会

【教材分析】

（一）编排结构

人教版小学数学教材中整数笔算除法的学习分三个阶段进行：从二下“有余数除法”（一层竖式）开始，到三下“除数是一位数的笔算除法”（两层、三层的分层竖式），最后到四下“除数是两位数的笔算除法”（两层、三层的分层竖式）。从知识之间的前后联系可以看出，在三下“除数是一位数的笔算除法”的教学中，学生将经历从一层竖式跨越到两层、三层分层竖式的过程，这是学习整数笔算除法的一个转折点和关键期。

“除数是一位数的笔算除法”内容丰富，包含了被除数是两位数和三位数以及有关0的除法，教材安排了5个课时进行新课教学（如图1）。

图1

教材的编排结构非常清晰：先编排一般情况的除法，再编排特殊情况的除法。但细致分析后会发现，教材中前4 个例题均指向“除哪商哪”（也就是“除到哪位就商在哪位”）的教学，在这3 个课时学习中，学生只需要关注并掌握这一个法则。而后面2 课时容量明显增加，如第4 课时，既要学习“除0商0”（也就是被除数首位刚好被除尽而被除数中间有0要商0，或被除数前两位刚好被除尽，而被除数末尾有0要商0），又要学习“不够商1就商0”（也就是“除到哪位不够商1 就商0”）。同一个课时中要掌握两个法则，对于学生而言极具挑战性。

（二）呈现方式

笔者从序、材两个方面，对“除数是一位数的笔算除法”的例题进行了梳理，在材料呈现上除关注是否编排情境外，还特别关注了是否有直观的、能够支撑算理解释的小棒图（如表1）。

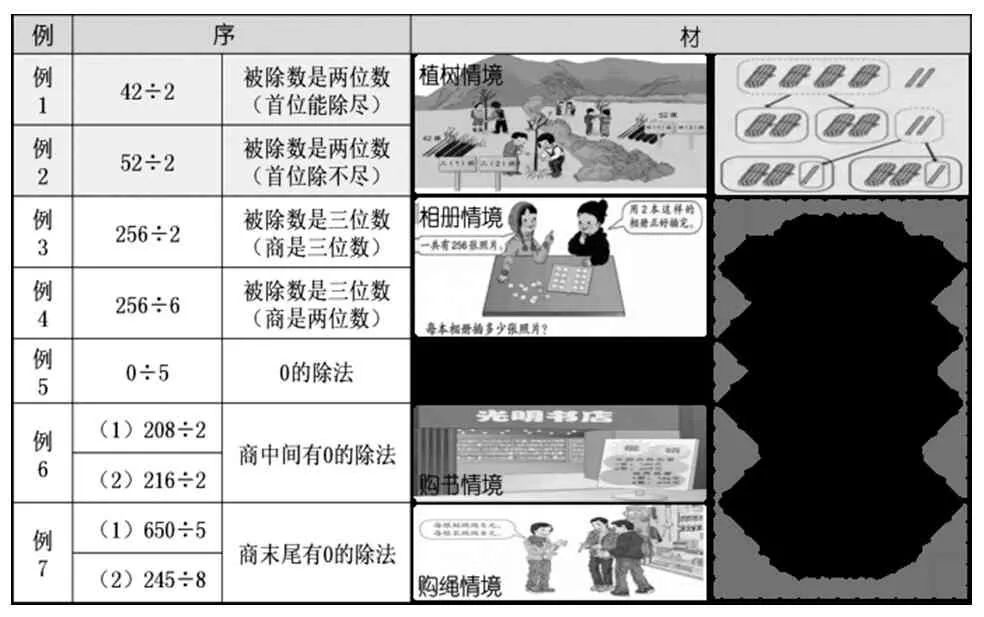
表1

从表1中可以看出，教材在笔算除法中分别安排了植树、相册、购书、购物等不同的情境，以有利于学生沟通数学与生活的联系。但教材只在“两位数除以一位数”学习时编排了小棒图辅助学生理解算理，掌握算法，而在更具挑战性的“三位数除以一位数”学习中，却仅仅提供情境，没有呈现有关算理支撑的信息。学生掌握“三位数除以一位数”远比“两位数除以一位数”困难，他们能基于前一节课的直观理解快速转换到“三位数除以一位数”的“就式论理”吗？这一点值得商榷。另外，教材中辅以理解的小棒图以“累加式”呈现（如图2），在分的每一步中，都会把前面分得的结果累加到下一次分的过程中。这样做的优点是能一下看出分得的最后结果，但对学生直观感知分了几次，每次分得多少却容易产生干扰。而除法是讲究一步一步除的，在除第二次的时候需要把第一次除掉的部分剥离出去，小棒图以“分离式”呈现（如图3）更有助于学生理解，即不同次分小棒的过程彼此分离，上一次分得的结果不再累加到下一次中。这样学生能更清楚地看到每次分小棒的情况，并将每次分小棒的情景对应到除法每层竖式的书写中，有利于学生对除法竖式意义的理解。

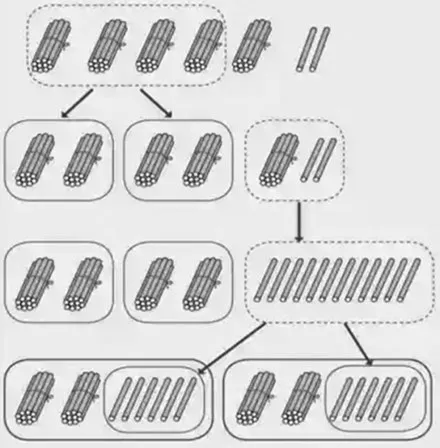
图2

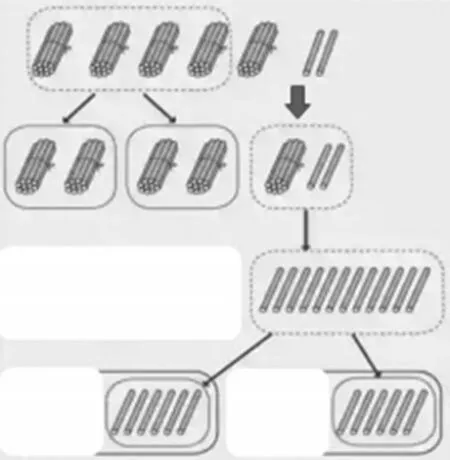
图3

基于以上分析，笔者在教学时考虑了以下两点：（1）在更具挑战性的“三位数除以一位数”学习中，增加辅助直观的小棒图。（2）变小棒图的“累加式”呈现为“分离式”呈现。

【学生情况】

通过前、后测调查发现，学生在“除数是一位数的笔算除法”的学习过程中容易出现以下4个方面的典型情况。

（一）受负面经验迁移影响大

负面经验迁移的影响主要来自于：（1）将加、减、乘法的竖式书写经验迁移到除法竖式中。（2）在首位没余数的除法中受一层竖式的负面迁移。具体如表2所示。

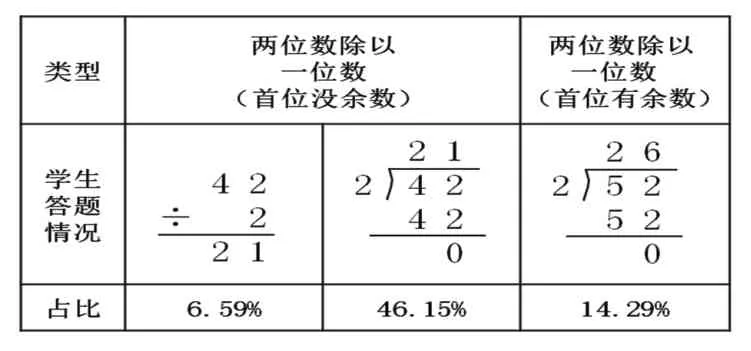
表2

（二）商0常会不简写

为了帮助学生理解商中间、商末尾有0的特殊除法竖式简便写法的原理，教材完整呈现了复杂竖式，并在竖式上用一层的空间详细表示了有关0 的计算全过程。并在右侧呈现简单竖式，以对比的方式引导学生学习（如图4）。但在后测中发现，基于由复杂到简单的教学路径，学生明白了除法竖式在书写时省掉“计算0 这一层”会更简单的道理之后，仍然会有一定比例（不同班级学生占比有所不同）的学生竖式书写时停留在了复杂的状态，常常会出现商0的除法竖式不简写的情况（如图5）。

（三）商0除法错误多

商有0的除法是学生特别容易出错、不易掌握的知识点。前测中学生的错误情况如图6 所示。这部分内容比较复杂，如从0在商中所处的位置上看，有“商中间有0”“商末尾有0”“商中间和末尾同时有0”的不同情况；从计算方法上看，既有“除0商0”又有“不够商1就商0”两种情况。因此教材在这部分内容的例题安排上，将近一半数量的例题编排在了商0的除法中。

图6

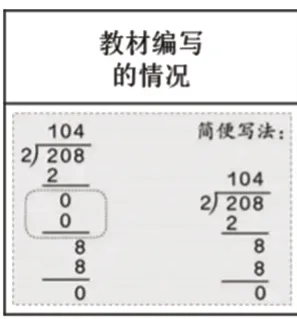
图4

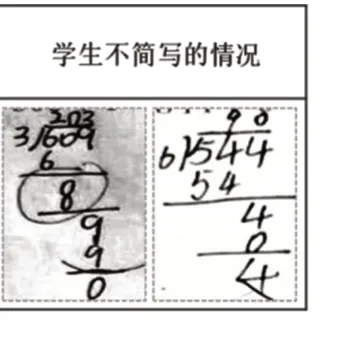
图5

（四）首位不够定位难

首位不够除的除法难就难在商的定位上。首位够除的三位数除以一位数竖式计算中，被除数和商都是三位，不存在商的定位问题，所以前测答题中虽然竖式计算步骤有所错误（虚线框部分），但商的定位并没有什么问题。而首位不够除的三位数除法中，商定位出错的占比较大（如表3）。

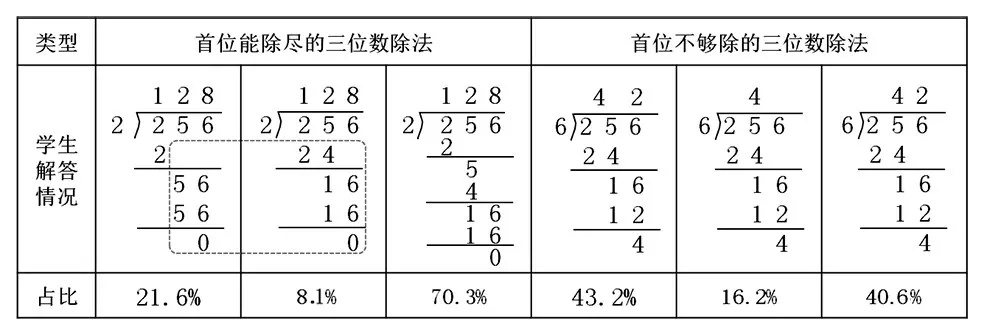
表3

【教学建议】

根据对教材编排及学生情况的分析，提出如下教学建议。

（一）局部调整建议

1.调序——减少负面迁移

教材例题编排的顺序是从“被除数是两位数，被除数首位能被除尽”的例题，到“被除数是两位数，被除数首位不能被除尽”的例题（如图7，情境图已略去）。

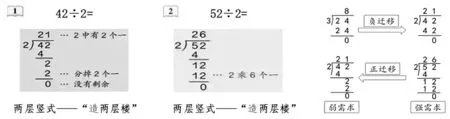
图7

由于学生的原有经验就是一层竖式，面对首位没余数的两位数除法，学生能轻易获得计算结果，从而容易受弱需求和负迁移影响写成一层竖式，反而觉得写两层竖式麻烦。因此，教师不妨调整学习序列，先教学例2再教学例1，这样更能激发学生对列两层除法竖式的强需求，减少一层竖式的负迁移。

2.调径——化烦琐为简单

如前文所述，学生在商有0 的除法竖式书写中，常会出现除法竖式不简写的情况。仔细阅读教材可以发现，教材在商0的章节中多处编排了如图8所示的从复杂到简单的教与学的路径，让学生充分经历复杂竖式书写的“烦琐”与“没必要”，从而更好地接受简便写法。如果借助小棒图从算理的角度学习，学生还需要这一“复杂”的过程吗？既然十位上一根小棒都没有，还要分吗？前测中，几乎没有学生会把单独的0 搬下来除一次，然后再商0 乘0 减0。既然如此，教师不妨根据学生实际调整教学路径，避开这一“烦琐”的过程。当然，这并不是说完全抛弃复杂竖式，而是当学生结合小棒图从算理角度理解了简单竖式的写法之后，再从算法角度让学生理解简单竖式书写的道理，进行繁简竖式的沟通就可以了。

图8

3.重组——集中突破重难点

商中间或商末尾有0 的除法，学生出现的错误比较多。结合前文教材分析，建议重组学习内容，将法则应用相同的内容归为一类，即“除0 商0”一节课，“不够商1 就商0”一节课（如图9）。这样重组，可以集中突破重难点，更利于学生对法则的掌握。

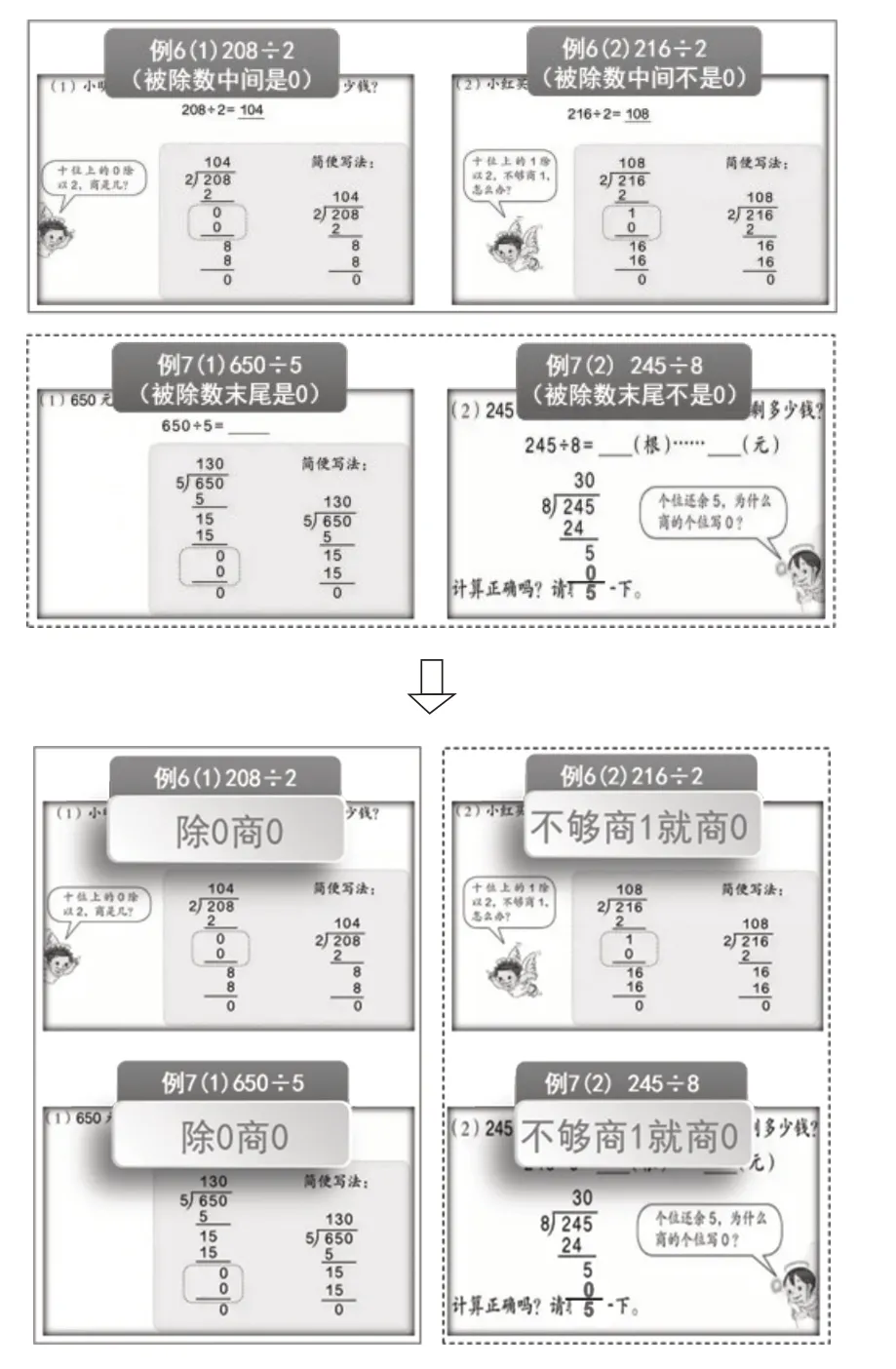
图9

4.整合——促进算理理解

教材编排中，首位不够除的除法是“三位数除以一位数”第二课时的教学内容。建议将这种情况理解成“首位商0”的除法，把它后移到商0 的除法中（如图10）。这样学生更容易理解既然百位上商是0，商首位（非0）就要写在十位上的道理。考虑到例7（2）245÷8 是首位和末尾同时商0 的情况，因此可以将例7（2）改为只有末尾商0的情况，如542÷3，而将245÷8首位和末尾同时商0的情况作为练习再呈现。

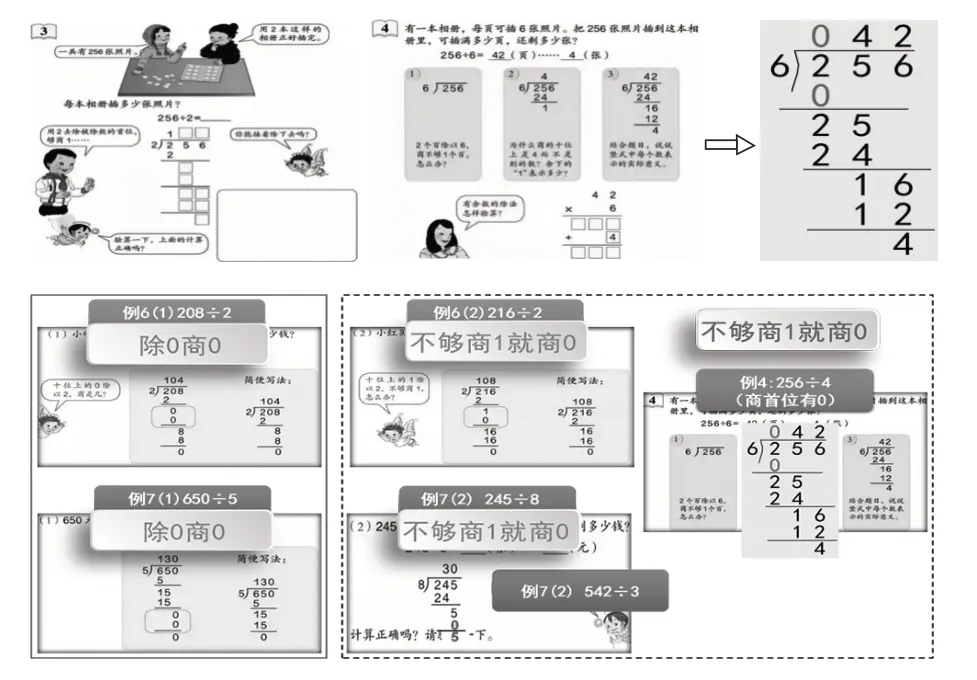
图10

（二）单元框架调整建议

综上内容，本单元教学的整体框架设计调整如下（图11）。

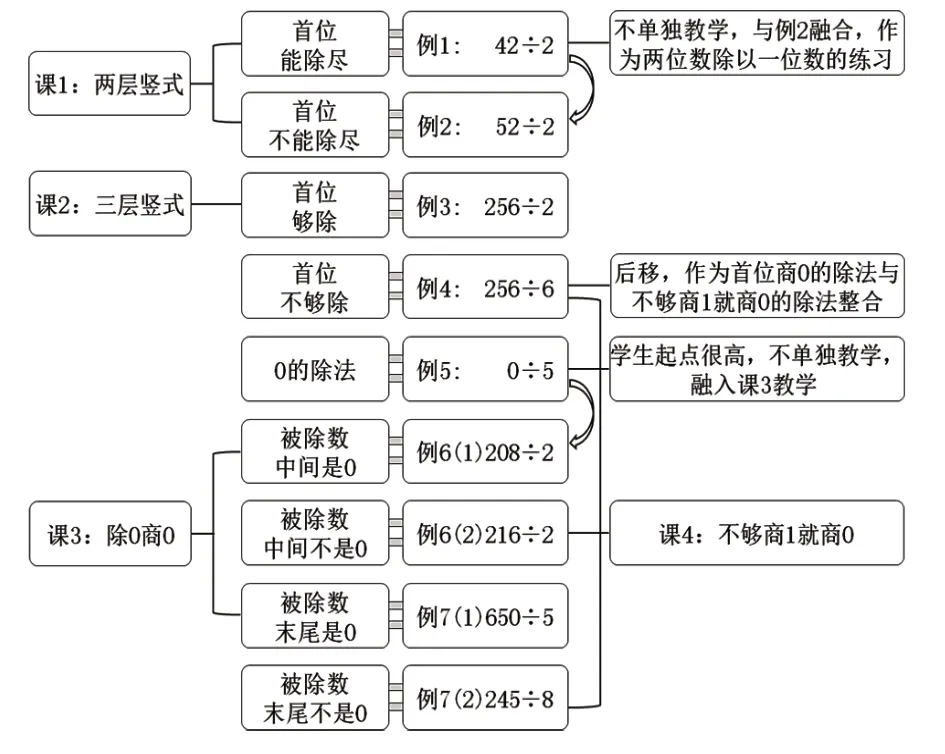
图11

教学课时调整如下（表4）。

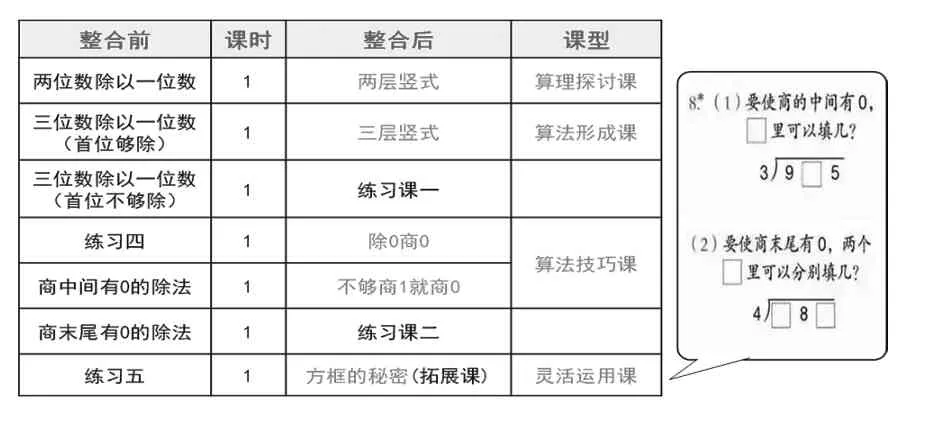
表4

这样调整，教学内容以“法则”为主线，将相关联的内容进行整合教学，在结构上形成了“算理探讨、算法形成、算法技巧和灵活运用”这4 个板块；在关联内容整合上进行“除哪商哪”“除0 商0”和“不够商1 就商0”的框架设计，并在整体遵循教材编排逻辑顺序的同时，将原来5节新课的教学内容整合成4 节新课进行教学。空出的一个课时可以本单元课后的思考题为素材，进行一题一课拓展，安排一节算理算法的灵活运用课，拓展学生思维，进一步培养和提升学生的运算能力，从而实现“让教师更有结构地教，学生更有关联地学”的目标。