弹子排加压机构的等应力参数设计与有限元仿真

王 雷，徐震宇，杨汇斌，车坚志

（内蒙古第一机械集团有限公司，包头 014000）

0 引言

弹子盘加压机构是一种“力矩—力”转化机构，它依据斜面传力原理，将推动转动盘的力矩转化为挤压移动盘的轴向力。弹子盘加压机构具有结构紧凑、强度高、增压倍数高的特点，因而在重载车辆全盘式机械制动器中得以广泛应用。受限于车辆的工作环境与行驶状态，弹子盘经常工作在非清洁、高温度的条件下，且承受巨大的表面压力。这样的工作状态会给弹子盘结构造成较大影响，因此也常发生弹子槽、弹子的磨损、压溃、烧结。

工程中，合理地设计弹子、弹子槽几何参数、尺寸公差、表面质量，保证加工精度，是限制二者间接触应力、提高承载能力，从而提高系统的工作可靠度、使用寿命的有效方法。

弹子排加压机构的设计受系统轴向压力需求和装配空间尺寸的限制，不同的设计输入导致弹子的受力状态不同。受限于材料性能的约束，弹子与弹子槽的接触应力需要限制在许用范围内；受限于工程造价的影响，更需要使加压机构较好的发挥材料性能。因此，合理地设计加压机构的几何参数使之保证不同受力状态下接触应力的均匀十分必要。

工程应用中，通常选择标准的钢球作为中间传力弹子，为其适应性地设计、加工弹子槽。作为非标准结构，弹子槽的布置方式、尺寸即为设计弹子排加压机构的重点。本文在工程应用背景下，对弹子槽曲率半径的尺寸公差进行优化，并使用有限元分析工具对计算结果加以验证，对指导工程设计有参考价值。

1 等应力参数设计

1.1 工作原理

如图1所示，弹子盘加压机构由三部分构成：转动弹子盘、移动弹子盘与弹子。转动弹子盘、移动弹子盘分别与弹子以定曲率弹子槽接触，弹子槽截面为完整圆弧，弹子槽中心线为右旋螺旋线，其深度随着扫略角度由深到浅。当转动弹子盘相对于移动弹子盘顺时针转动（从有弹子槽的一侧看转动弹子盘）时，转动弹子盘与移动弹子盘弹子槽之间产生角度错位，在弹子尺寸的限制下，两弹子槽间隙不能改变，迫使移动弹子盘沿轴向远离转动弹子盘，推动制动摩擦片挤压制动盘。当移动弹子盘达到位移上限时，弹子盘结构不再产生相对运动，弹子槽与弹子之间的正压力逐步加大，直到与外部轴向支撑力达到平衡。

图1 弹子排加压机构

1.2 几何约束

弹子排加压机构的设计输入主要包括以下几点：

1）径向、轴向尺寸；

2）移动盘的轴向位移空间；

3）转动盘的转动角度；

4）轴向压力需求；

5）可提供的转动盘驱动转矩。

其中1）、2）、3）项共同决定了系统设计的几何约束：转动弹子盘转动一定的角度，不同分布圆周上的弹子球心升程相同，才能保证移动弹子盘有恒定数量的轴向支撑。弹子排加压机构的几何参数示意如图2所示，各几何参数之间相互影响关系如图3所示。

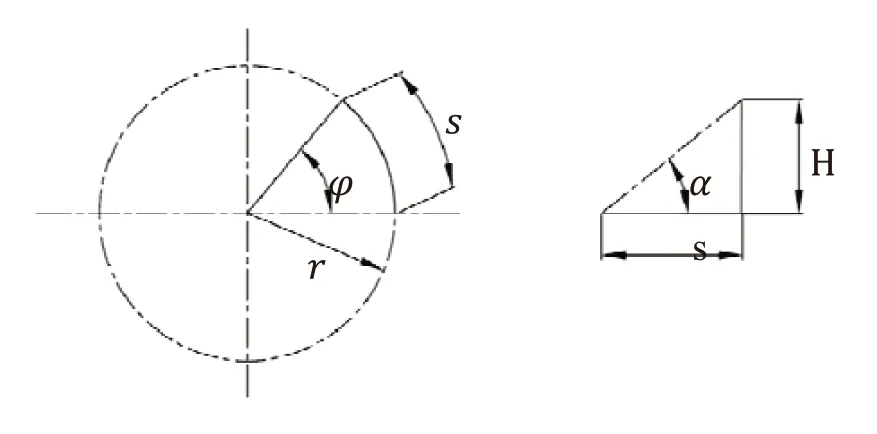
图2 几何参数示意

图3 弹子排加压机构几何参数之间的影响关系

可以推导弹子排加压机构几何参数之间的函数关系如式(1)所示。

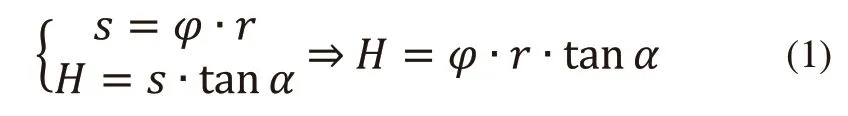
式中，s为球心轨迹弧长，φ为球心扫略圆心角，r为弹子球心分布圆周半径，H为球心升程，α为球心轨迹的螺旋升角。

1.3 等应力约束

1.3.1 斜面传力的分解：

斜面传力理论图示如图4所示，轴向力Fa、正压力FN之间满足式(2)所示的关系。

图4 斜面传力分解示意

根据三角函数的关系：

可得弹子所受的正压力FN、有效的轴向支撑力Fa与弹子球心分布圆周半径r之间的关系：

同一弹子盘结构中，升程H、扫略角φ相等，在假设弹子盘为绝对刚体的条件下，轴向压力（Fa）相等，弹子受到的正压力随弹子分布圆周半径r的增大而减小。

1.3.2 接触应力

对于弹子直径Dw、弹子槽半径R的接触结构，基于赫兹理论进行接触应力计算如下：

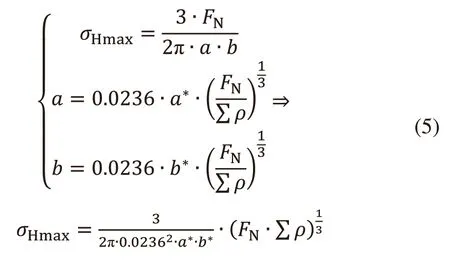
式(5)中，σHmax为赫兹应力峰值，a、b分别为椭圆形影响区域长半轴、短半轴，a*、b*分别为长半轴、短半轴系数，∑ρ为接触区域曲率和函数。

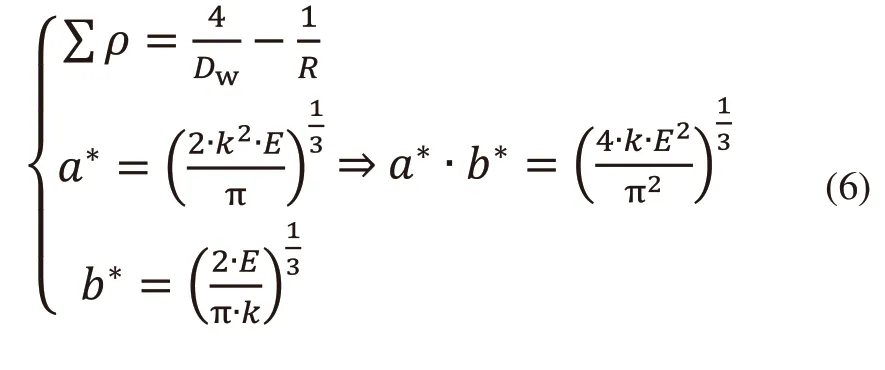
式(6)中，k为接触域椭圆偏心率系数，E为第一类完全椭圆积分近似公式：

式(7)中，Rx、Ry分别为第一x向、y向主平面内的有效半径：

式(8)中，f为半径比例系数：

1.4 接触应力与几何参数的关系

为了探究弹子槽曲率半径、弹子球心分布圆周半径对接触应力的影响，基于赫兹公式进行接触应力的计算。

计算基于下述两点假设：

1）选用的标准化钢球直径绝对统一、标准，为28.575mm；

2）弹子盘（移动弹子盘和转动弹子盘）刚度足够，轴向压力由盘间各个弹子均匀承受。

接触应力的计算参照包括：

1）以弹子球心分布圆周半径160mm的弹子排为基准弹子排；

2）以弹子槽半径29mm为基准弹子排槽半径；

3）每个弹子提供轴向支撑力1000N；

4）以基准弹子排接触应力峰值的±5%设置应力浮动范围。

设置两个计算组，分别为1组（弹子球心分布圆周半径100mm）、2组（弹子球心分布圆周半径130mm），计算结果如图5所示。

图5 弹子槽曲率半径与接触应力的关系

依据接触应力、弹子槽半径之间的关系，可以计算保证接触应力在给定区间（基准排接触应力峰值±5%）内的弹子槽半径，如表1所示。

2 参数化模型的有限元仿真

2.1 参数化建模

由于弹子槽中心螺旋轨迹的半径、螺旋升角之间要满足2.2节中所述的几何约束关系，不同分布圆周上的弹子槽半径受2.3节中所述等应力约束条件限制，使用参数化的三维建模工具是较准确和方便的。根据2.2节、2.3节中对结构几何参数关系的描述可知，弹子排加压机构的设计输入参数包括弹子球心分布半径、弹子槽半径、弹子槽中心螺旋升角。其中，设计排的弹子槽螺旋升角由基准排弹子槽螺旋升角以及基准排、设计排的弹子球心分布半径决定，设计排弹子槽半径依据2.3节中所述的计算方法确定。如图6所示为Creo平台上的参数设置窗口，图7为三维参数化模型。

表1 弹子排加压机构几何参数与接触应力的关系

图6 参数设置窗口

图7 参数化三维模型

2.2 有限元仿真

2.2.1 网格划分

由于弹子周向均布，仿真计算中可以认为同一排弹子的受力情况相同，所以截取扇形区域对上述模型进行简化，再导入ANSYS中进行网格划分。

由于有限单元法采用多边体逼近曲面，多边体网格的尺寸直接影响了计算精度，划分的网格尺寸越小，计算越精确，但是计算所占用的内存、时间越多。综合计算考量计算精度与计算经济性，按照经验，单元尺寸与接触域最大形变量相近为宜。

根据2.3中的计算，椭圆影响域的长轴最小值约为8mm，短轴的最小值约为0.78mm。为了在保证计算精度的前提下节约计算空间，将弹子、弹子槽表面网格尺寸设置为1.5mm，仅对接触区域进行网格细化，细化单元尺寸为0.75mm，如图8所示。

2.2.2 模型设置

为简化后的轴对称体设置轴对称特征，在转动的弹子盘轴线上（轴向位置任意）设置局部坐标系，将扇形区域的左右两断面设置为对称边界，如图9所示。

2.2.3 边界条件

固定移动弹子盘下表面，在转动弹子盘上表面施加1000N的轴向压力，转动弹子盘外侧圆柱面设置圆柱支撑，约束转动弹子盘的转动、径向偏移自由度，仅释放轴向移动自由度，边界条件设置如图10所示。

2.2.4 仿真结果

图8 网格划分

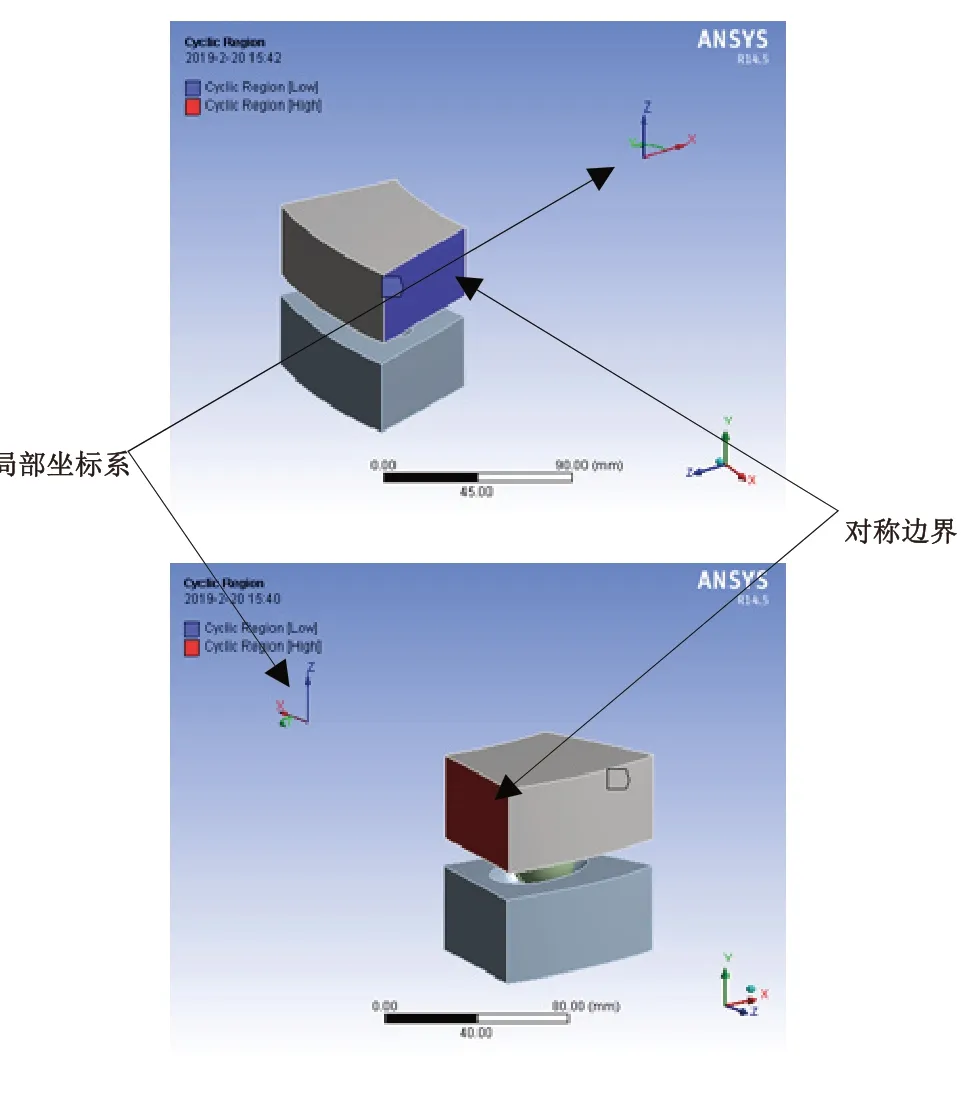
图9 轴对称特征设置

图10 边界条件

按照表1中的参数，在Creo平台上依据三种弹子分布圆周半径，设置三种弹子槽半径，生成三组参数下的装配体模型，导入ANSYS中运行9组静态结构分析（Static Structural）。表2～表4统计了接触应力（Contact Pressure）的仿真试验结果，以及仿真结果与赫兹公式的计算结果的相对误差。

表2 仿真结果（0组，弹子分布圆周半径160mm）

表3 仿真结果（1组，弹子分布圆周半径100mm）

表4 仿真结果（2组，弹子分布圆周半径130mm）

2.3 结果分析

2.3.1 结果对比

由表2～表4中的数据可知：

1）弹子与弹子槽的接触域呈狭长的椭圆形，接触应力自椭圆边缘向中心递增，符合赫兹接触的特征；

2）九组试验中，接触应力的有限元仿真计算结果与赫兹应力计算结果的相对误差较小，除0组等应力条件的试验组达到了4.177%，其余八个试验组皆在3%以内，两种计算结果体现出了较高的一致性。

综上所述，认为2.4中关于几何参数与接触应力之间关系的计算符合实际工况，采用基于赫兹公式的计算方法确定弹子槽参数关系是科学的。

2.3.2 弹子槽直径的公差设计

为了便于生产执行，规范工艺管理，需要将表征弹子槽曲率的半径值转化为弹子槽直径值，再按照国家标准，将该值进行标准化。为保证标准公差下的结构能够满足±5%的应力限制，对直径上下偏差的限制不得宽于理论计算值。三组标准化的弹子槽直径公差如表5所示。

表5 弹子槽直径公差的标准化

3 结语

弹子排加压机构中，弹子槽与弹子之间的接触符合赫兹接触。弹子槽与弹子的曲率半径直接影响二者的接触状态、接触应力峰值。不同的设计输入条件下，会引起弹子、弹子槽的受力状态变化。以不同受力状态中，二者间接触应力的统一为优化目标，使用赫兹公式可以推导不同设计参数间的关系，从而计算合适的弹子槽曲率范围。在工程中，依据计算的弹子槽曲率范围，可以指导弹子槽直径的公差设计，从而有效地控制弹子与弹子槽之间的接触应力，提高系统寿命。