基于改进直接模糊自适应反馈控制的多移动机器人编队算法

李海婷 ，张鹏超 ，任肖辉 ，罗朝阳 ，呙生富

（1.陕西理工大学 电气工程学院，汉中 723000；2.陕西理工大学 陕西省工业自动化重点实验室，汉中 723000；3.陕西理工大学 机械工程学院，汉中 723000）

0 引言

移动机器人编队控制作为一项多机器人完成既定任务的基础技术，需要通过控制器对每个机器人进行实时控制形成一定队形的同时保持队形的稳定，是多智能体领域的重要研究方向之一。常用的编队控制方法有跟随领航者法[1]、人工势场法[2]、基于行为法[3]等其他混合控制方法，随着人工智能技术的发展，一些智能控制方法如遗传算法[4]、粒子群优化算法[5]、差分进化算法[6]、模糊控制[7]、神经网络控制[8]等被应用到多智能体编队中来，其中遗传算法、粒子群优化算法、差分进化算法属于同一类型的路径搜索算法，会出现局部最优、死锁问题；迭代学习控制需要考虑初始值和鲁棒性问题；神经网络存在的“黑匣子”、学习速度慢等问题，自适应模糊控制法因其不依赖于被控对象的精确模型、鲁棒性和适应性好、易于软件实现的特点被广泛应用。

传统的模糊控制法已在多移动机器人编队控制中得到应用，虽然可以满足控制系统对实时性、自适应调整的要求，但在编队过程中仍会出现控制精度差、自适应能力有限、容易产生振荡现象等问题。为此，Chang[9,10]提出一种自适应模糊滑膜编队控制器，提高了系统的自适应性，但响应时间明显增加；Handayani[11]在此基础上利用模糊逻辑控制很好的保持了队形的稳定，缩短了系统响应时间，但没有考虑外界的扰动因素，控制精度有待提高，Chen[12]提出一种分布式模糊一致性控制策略，考虑了未知因素的影响，提高了控制精度，但出现了超调且误差收敛速度较慢的问题，无法达到最优控制。

本文针对以上控制方案的缺点，提出一种基于改进模糊自适应输出反馈编队控制方法，在建模时考虑外界因素的影响，设计控制器对多个状态量进行自适应调整逼近理想状态，并且利用Lyapunov理论保证控制系统的稳定性，加快误差收敛速度，提高系统的控制精度。

1 移动机器人的运动-动力学模型

针对Kobuki机器人建立模型，机器人底盘主要由两后轮和一个前轮组成，后轮用来驱动，前轮用来平衡系统和控制转向。如图1所示，其中G为质心，B为两后轮基线中心点，H（x，y）为被跟踪与主动跟踪轨迹的几何中心点，v和分别为质点G的纵向、横向线速度，w和θ为h点的角速度和航向角。Frlx和Frly为左轮受到的力，Frrx和Frry为右轮受到的力，Fcx和Fcy为C点脚轮受到的力，Fdx和Fdy为机器人受到的未知外部力（工具、扰动等），m为机器人的质量，Iz为G点垂直轴的转动惯量。

图1 移动机器人运动-动力学模型

由图1可得机器人的力和力矩方程：

H点的运动学方程为：

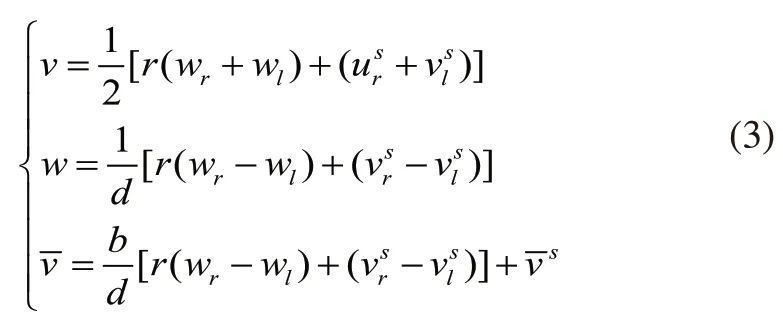
其中r为车轮半径，wl和wr为左右两轮的角速度，为左右轮的纵向滑移速度，为横向滑移速度。

移动机器人电机模型为：

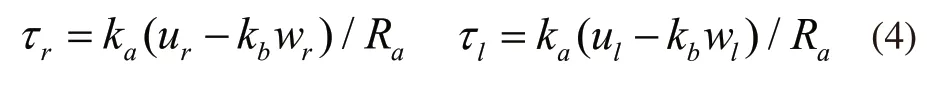
其中ul、ur为输入左右电机电压，ka为电压常数乘以传动比，Ra为电阻常数，τl和τr为左右电机转矩乘以传动比，kb是转矩常数乘以传动比。

电机-车轮的动力学方程为：

Ie和Be为车轮绕轴的转动惯量和驱动电机转系到车轮的粘性摩擦系数。

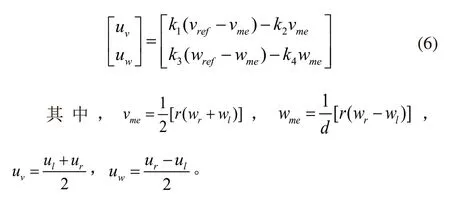
联立式(1)～式(6)得：

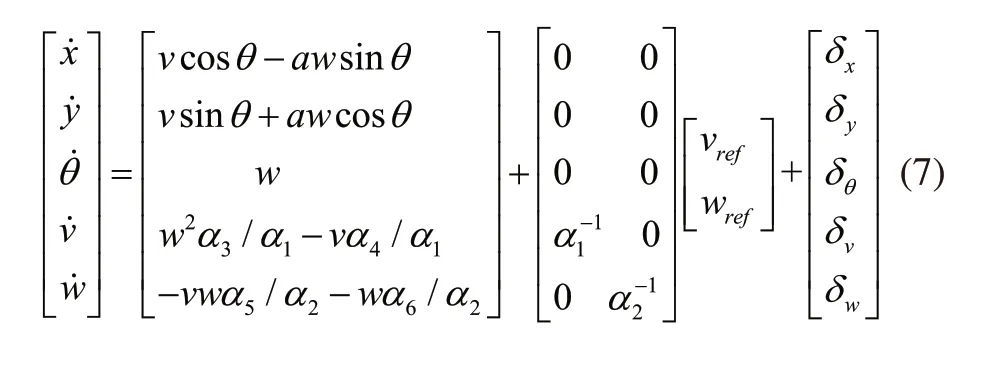
其中：

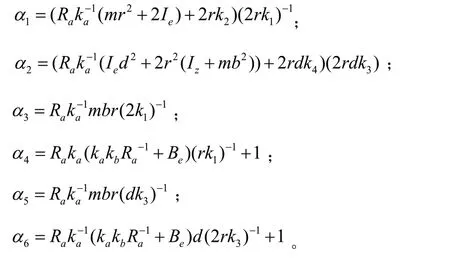
2 控制器的设计

为了避免过度依赖领航者和链式结构造成的跟随者误差累积问题，本文采用虚拟领航者法，运动模型如图2所示。

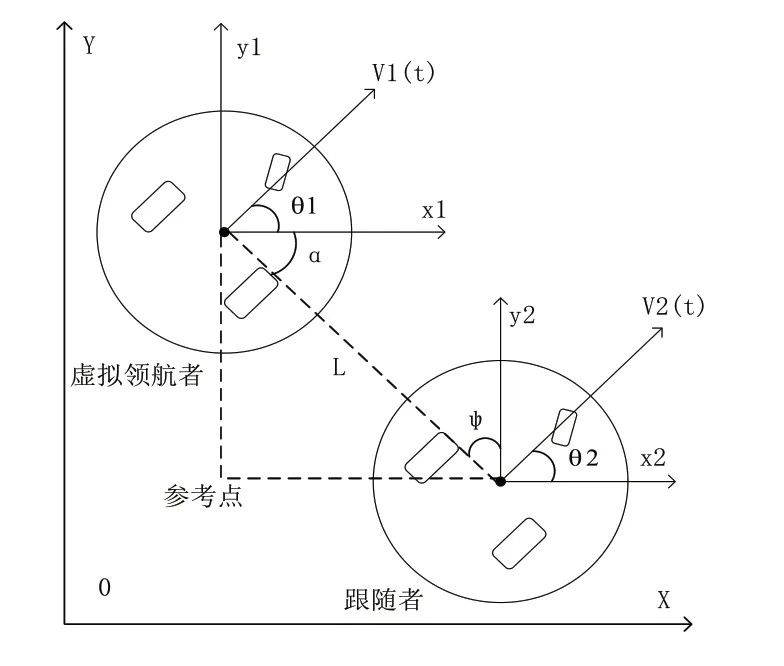
图2 虚拟领航-跟随者运动模型

设虚拟领航者的状态向量为[x1，y1，θ1，v1，w1]，跟随者的理想状态向量为[x2，y2，θ2，v2，w2]，由图2可得：

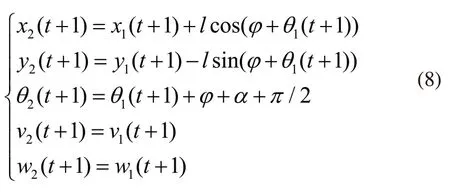
给定虚拟领航者的运动参数，由式(8)得每一个机器人的理想运动参数，作为模糊控制系统的逼近目标。

2.1 模糊分级

控制规则的选择是模糊控制器设计中的一个基本问题。模糊规则分级复杂度直接影响系统响应速度、稳定性和控制精度。选择合适数量、复杂程度适当的模糊级至关重要。将状态量模糊级分为7级，考虑控制灵敏度和偏差大小，选取三角形隶属函数。模糊子集划分如表1、表2所示，隶属度函数如图3所示。

表1 x，y，θ，v，w的模糊子集划分

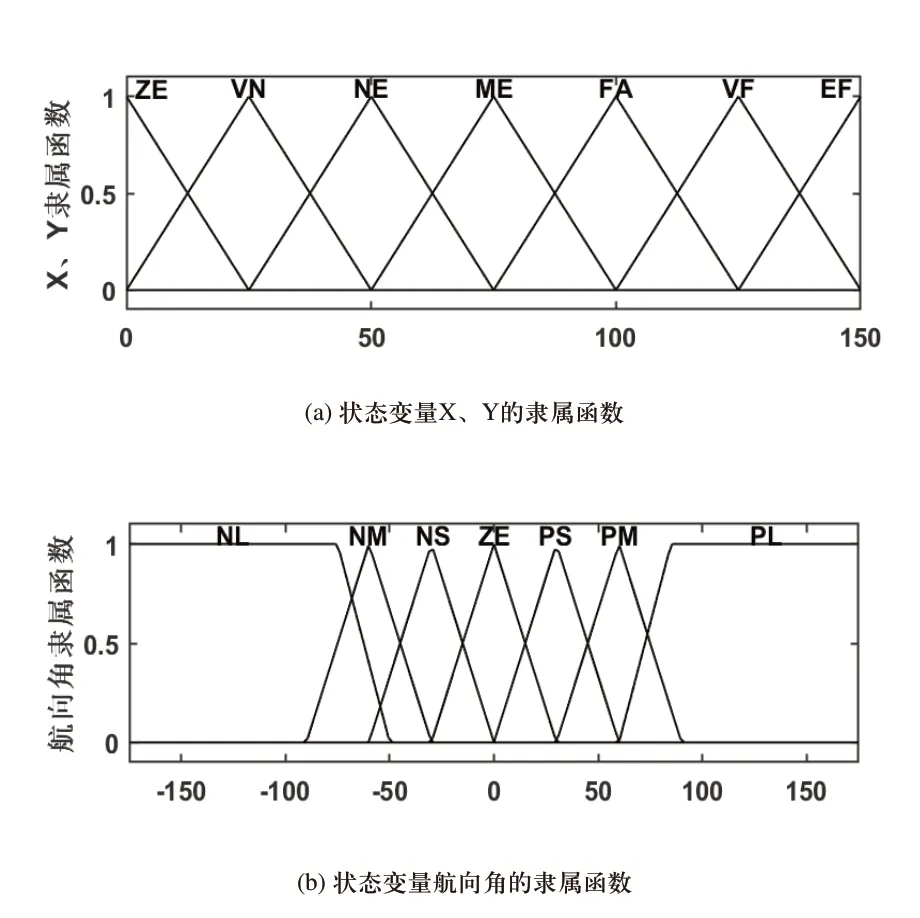
图3 状态变量的隶属函数

2.2 直接模糊自适应控制器的设计

2.2.1 问题描述

为方便直观的设计控制器，对单个机器人控制系统位姿进行整体描述。设状态向量x=[x，y，θ，v，w]T，则，由系统状态方程(7)得：

设y=x=[x，y，θ，v，w]T，研究对象可表述为：

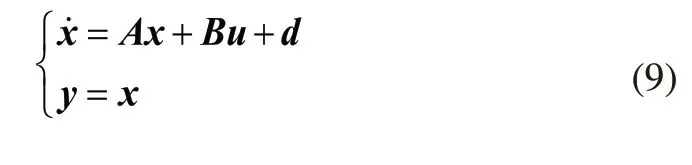
设状态指令为ym=[xm，ym，θm，vm，wm]T，令e=ym-y=ym-x，e=[e1，e2，e3，e4，e5]T，对变量xi（i=1，2，3，…，n）定义mi个模糊集合Aili（li=1，2，…，mi）， 用以下条模糊规则来构造模糊系统u。

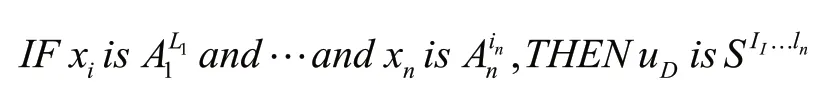
其中li=1，2，…，mi，i=1，2，…，n。

设系统总体控制u为基本控制uc（x|θ）和监督控制us（x|θ）之和：u=uc（x|θ）+us（x）。uc、us为模糊函数，θ为可调参数集合，式中uc为模糊逻辑系统，采用乘积推理机、单值模糊器和中心平均解模糊器设计模糊控制器为：

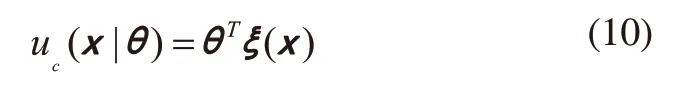
其中ξ(x) 为维向量，第l1，…，ln个元素为

其中|f(x)|<=fu（x），0≤BL≤B，依系统稳定情况取0或1。

取控制率为：

将式(10)、式(11)代入式(9)整理得：

通过K的选取，可使t→∞时，e(t) →0，使系统的输出状态渐进收敛于理想输出状态。

2.2.2 模糊自适应算法

定义最优参数为：

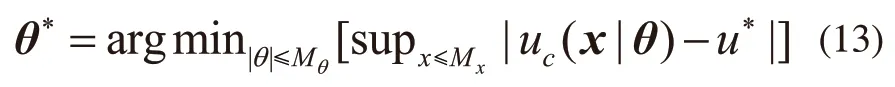
最小模糊逼近误差为s=uc（x|θ*）-u*，Δ=-KT，由式(12)、式(13)可得：

取参数θ的自适应律为：

为了保证|θ|≤Mθ，使用投影算法来修正自适应率(15)如下：

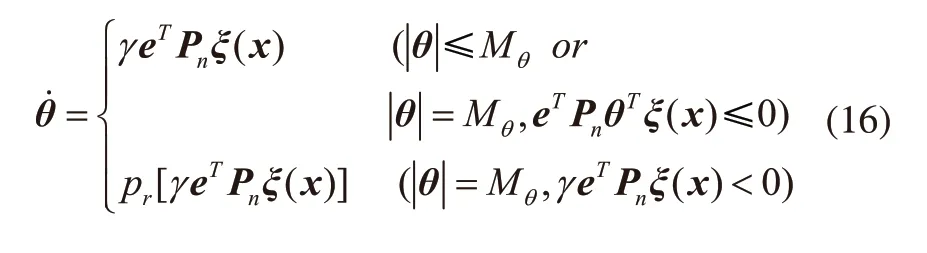
式中pr[*]为投影算子，定义为：

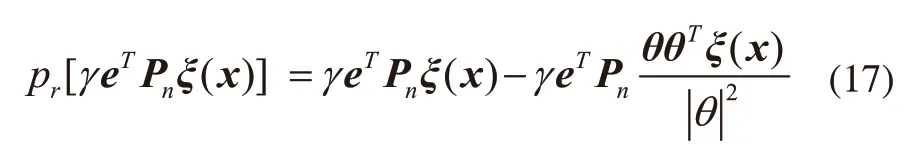
γ是正的常数,pn为正定矩阵p的最后一列，可得eTPB=eTPn。

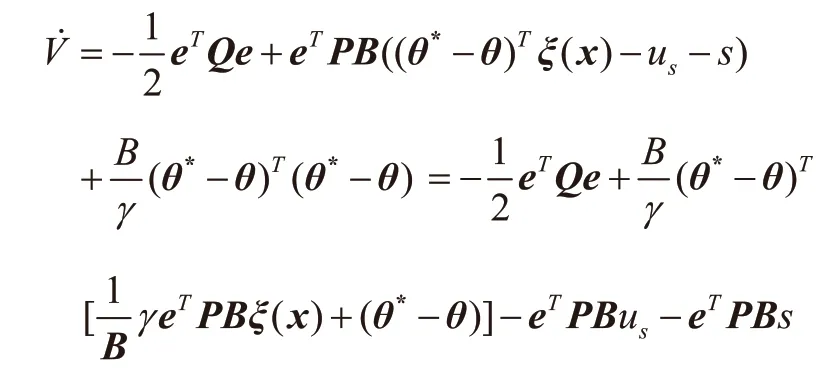
由式(16)、式(17)得：

经证明最后一项为负，因此有：

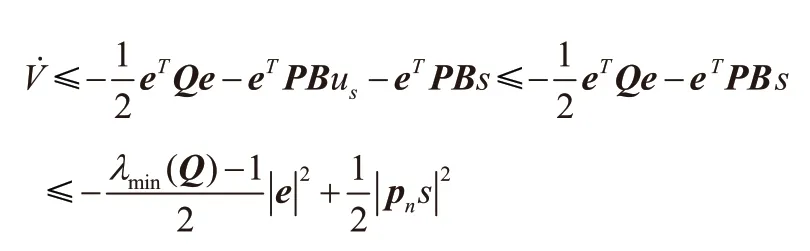
上式两边对t积分并整理得：

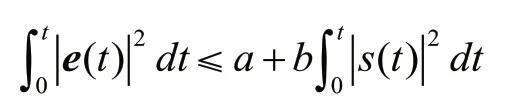
其中：

综上机器人系统在控制律作用下保持稳定。直接自适应模糊控制结构如图3所示。

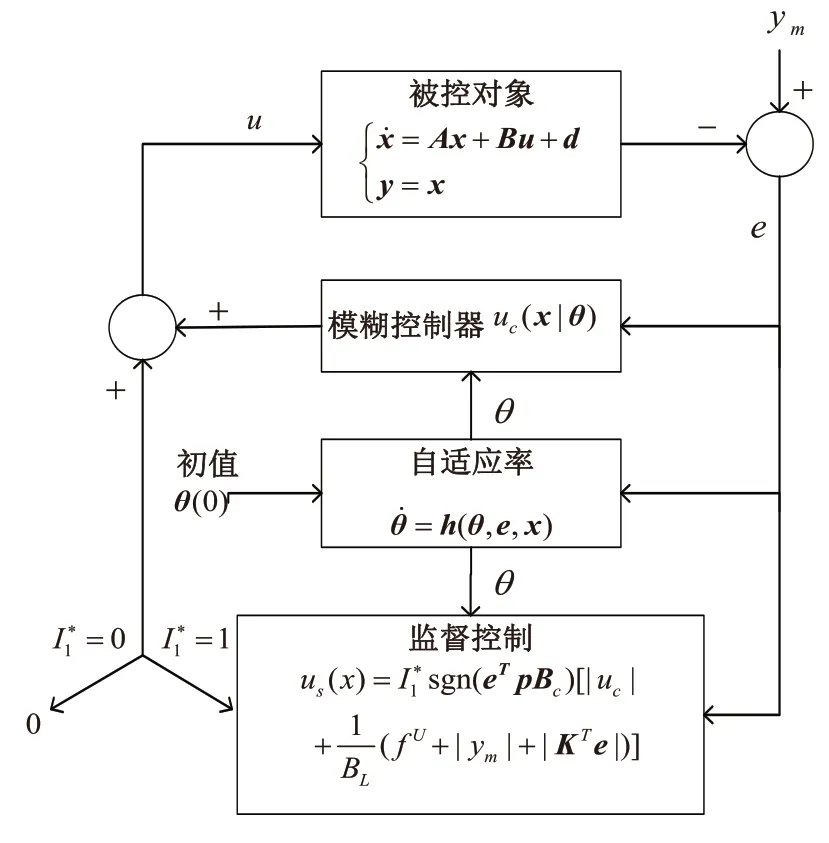
图4 直接型自适应模糊控制系统

3 实验验证与评价

为了证明该改进直接模糊自适应控制方法的有效性，由仿真实验进行验证。设定虚拟领航者初始状态向量为[x，y，θ，v，w]=[1，1，0，1，π/180]，设定机器人参数为a=0.1，l=10，α1=0.1736,α2=0.1673，α3=0.003，α4=0.6643，α5=0.0018，α6=0.7179，仿真时间T=100s。控制目标是在外界未知扰动因素影响下，通过控制输入使机器人输出状态实时跟踪机器人系统的期望状态，控制误差收敛在原点附近小领域内。θ中各元素的初始值均取0，采用控制律式(10)，自适应律式(15)，取Q=50，自适应参数γ=50。仿真结果如图5～图7所示。

图5 弧形编队轨迹图 图6跟随者1速度、位姿误差曲线图

图6 跟随者2速度、误差曲线图

图7 传统模糊控制法跟随者位置误差

图5为两个机器人跟随虚拟领航者leader实现的弧形编队轨迹图，图6、图7分别为两个跟随机器人的线速度、角速度、位置误差，图7为传统模糊逻辑控制法编队中跟随者的位置误差。由图5可得改进的直接模糊自适应控制算法实现了多移动机器人的编队，证明了控制方法的有效性；由图6和图7可得：直接模糊控制法下跟随者1、2的线速度与角速度很好的跟踪了理想线速度0.5m/s、角速度0.1rad/s，位置误差整体在0.1m左右浮动，相比于传统模糊逻辑控制法，位置误差精度提高了30%，误差收敛速度明显加快。表明了多移动机器人系统在设计的控制器作用下实现编队并稳定的跟踪理想轨迹保持队形。

4 结语

针对非线性复杂系统的传统模糊控制算法适应性差、控制精度低的问题，提出一种基于直接模糊自适应反馈控制的多移动机器人编队控制算法。对kobuki机器人组成的多机器人控制系统进行运动-动力学建模与分析，确立模糊规则、进行模糊逻辑推理和稳定性的分析与证明，并利用仿真实验验证。实验结果表明，该算法相对于传统模糊逻辑控制法，增强了控制系统的适应性和稳定性，使控制误差快速收敛在原点的领域内并保持稳定，控制精度平均提高30%以上，对多移动机器人编队控制队形的形成和保持具有一定的应用价值。