干片式制动器弹子加压装置的力传递效率研究

王延忠， 贾树王， 郭超

(北京航空航天大学 机械工程及自动化学院，北京 100191)

弹子加压装置并不是一个新型结构，其因具有结构紧凑、机械增力、制造成本低等特点很早就用于重型车辆制动系统中[1-3]. 陈文滨[4]对弹子加压装置进行了试验研究，分析了弹子加压装置所用材料与载荷对力传递效率的影响.李传奇[5]仿真模拟了弹子槽结构对装置的力传递的影响趋势，优化了弹子槽尺寸与弹子槽螺旋角的设计参数. 兰海等[6]研究弹子槽表面的形貌特征，通过在弹子槽表面喷涂镍石墨涂层来增加弹子槽的力传递能力.

虽然前人进行了大量的试验、仿真等研究，但是到目前为止对弹子加压装置的力传递特性及传递力损失现象仍然难以完全被解释清楚. 这主要是由于弹子加压装置结构复杂、弹子滚滑运动形式不唯一、摩擦元件制动过程位移变化不明了. 本文从弹子加压装置的结构出发，假定摩擦元件为拟静力平衡运动状态，分析弹子加压装置运动过程中装置外部与机架的摩擦阻力和装置内部弹子结构的传力特性，并通过对弹子加压装置力传递效率的计算，分析了力传递损失的主要影响因素，为弹子加压装置的优化指明方向.

1 弹子加压装置结构分析

弹子加压装置运动类似于滚珠丝杠运动副，主要形式是将旋转运动转化为直线运动，并把扭矩转换为轴向作用力. 如图1(a)所示为制动系统中的弹子加压装置,由转动盘、弹子、移动盘组成. 图1(b)是弹子加压装置的局部放大图. 需要制动时，转动盘旋转特定角度，弹子在弹子槽中运动，移动盘下压压紧摩擦元件进行制动.

弹子加压装置单个作用周期可以划分为两个阶段：①弹子加压装置未对摩擦元件施压前的运动阶段，即图1(b)中移动盘处在阶段分界线g以上位置时；②弹子加压装置对摩擦元件施压后的运动阶段，即图1(b)中移动盘处在阶段分界线g以下位置时. 阶段①弹子加压装置运动响应迅速、无负载，为非工作阶段，力传递损失可以忽略，本文并不研究；阶段②中的弹子加压装置运动缓慢、存在摩擦元件负载，为正常工作阶段，其力的传递损失直接影响了摩擦元件的摩擦特性，是本文研究的对象.

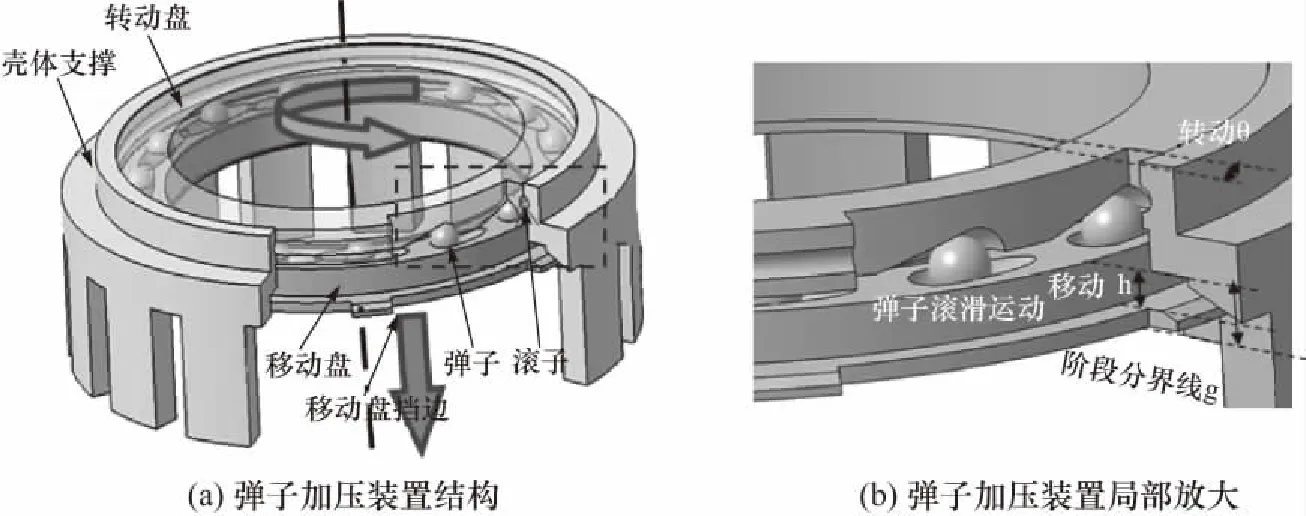
图1 弹子加压装置Fig.1 Marbles screw loading device

2 弹子加压机构的力传递损失分析

当弹子加压装置处于阶段②中时，它的运动缓慢，假设为拟静态过程，符合静平衡受力条件. 根据运动与受力关系，可以把装置简化为如图2所示的模型. 模型中驱动力推动转动盘沿x轴运动，转动盘压紧弹子，弹子推动移动盘沿y轴运动，壳体转化为机架限制机构自由度. 从简化模型可以看出弹子加压装置的力传递损失主要在如下二个部分：①弹子加压装置与机架(制动器壳体支撑)之间的摩擦阻力损失，主要包括转动盘与壳体接触损失和移动盘与壳体接触损失；②转动盘与移动盘之间弹子接触力传递损失，主要表现为装置的偏置加载. 为探明各处损失对装置的力传递影响情况，下面分别对各处损失特性进行分析.

图2 弹子加压装置简化Fig. 2 Diagram of the marbles screw loading device

2.1 弹子加压装置与壳体的摩擦阻力损失

2.1.1转动盘与壳体的接触摩擦损失

转动盘与制动器壳体是铰链连接，之间填充滚珠减小摩擦力，即壳体对弹子加压装置的摩擦阻力由滚珠的滚动阻力构成,如图3所示.

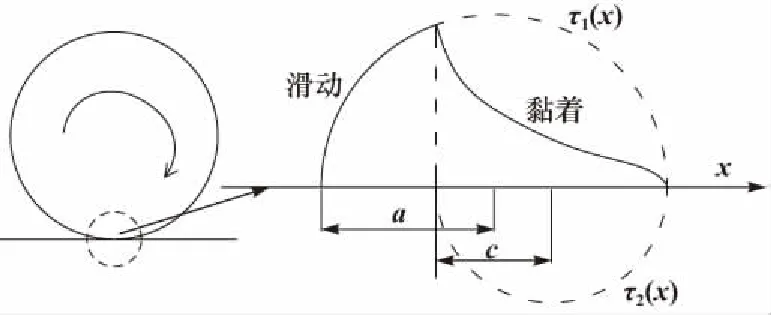
图3 滚动接触面切应力分布Fig.3 Shear stress distribution of rolling contact

根据滚动接触理论，滚珠的滚动阻力与滚珠的接触面黏滑状态相关，表示为

(1)

式中:f为摩擦力；μ1为库伦摩擦因数；P为滚珠所受正压力；c为滚珠黏着接触区等效半径；a0为滚珠接触区等效半径.

假设n2个滚子之间并不相互作用且受力相同，则由式(1)可以得出滚珠对弹子加压装置的反作用摩擦阻力f1为

(2)

式中：f1为滚子处装置的摩擦阻力；μ2为滚子摩擦因数；F1为滚子受到的轴向压力.

2.1.2移动盘与制动器壳体的接触摩擦损失

移动盘与制动器壳体的连接是滑动副连接. 根据库伦摩擦定理，制动器壳体对弹子加压装置造成的摩擦阻力为

f3≤μ1M2/L5,

(3)

式中:f3为挡边处装置的摩擦阻力；μ1为库伦摩擦因数；M2为机架阻碍移动盘的力矩；L5是移动盘挡边接触位置半径.

2.2 转动盘与移动盘之间弹子接触力传递损失分析

转动盘、移动盘、弹子三者共同构成了弹子加压装置，三者之间的摩擦阻力是装置内部作用力，并不会造成力的传递损失. 但是弹子在弹子槽中分布存在随机性(见图4(a))，即各个弹子所处弹子槽中位置不同，会造成所有弹子轴向分力的合力矩存在倾覆力矩、切向分力的合力不为零，从而装置偏载导致力传递损失. 下面分别分析弹子造成的倾覆偏载与切向分力的合力，并计算力传递损失.

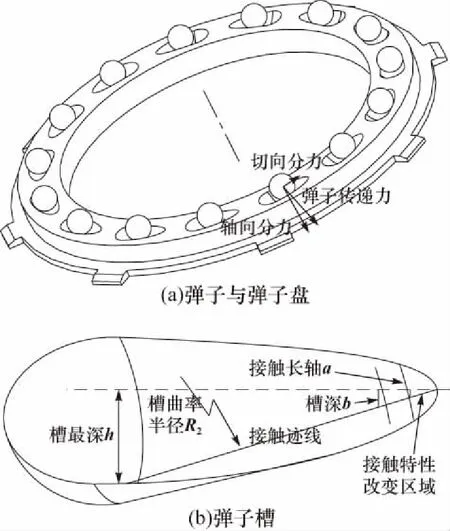
图4 弹子盘结构Fig.4 Marbles plate

2.2.1弹子造成的倾覆偏载对装置力传递的影响

由于弹子槽曲面宽度是变化的(如图4(b)所示)，因此相同载荷下弹子与不同弹子槽位置接触时接触区域变形不同，会使装置产生协调变形，从而额外产生倾覆力矩造成装置偏载，影响力的传递效果. 针对这种概率与弹性接触共同作用造成偏载的复杂问题，文中通过比较弹子槽赫兹接触区域与非赫兹接触区域的大小来量化装置的倾覆力矩偏载情况. 因为弹子槽赫兹接触区域越大，弹子位于该区域的概率越大，又由同尺寸下赫兹接触变形只与接触力有关，因此各个弹子槽接触变形一致的概率越大，对装置的偏载越抑制，对装置的力传递效率越好.

假设转动盘传递给弹子的力是均匀的，相对于只考虑弹子传递给移动盘的力的差异. 因此对单个弹子与弹子槽的接触特性进行分析，划分弹子槽赫兹接触区域与非赫兹接触区域.

首先假设接触为赫兹接触，则由赫兹接触公式表示为

(4)

(5)

假设接触长轴a完全占满槽宽时，弹子与弹子槽的接触不再符合赫兹接触假设，则赫兹接触与非赫兹接触的分界点处的槽深b(如图4(b))表示为

(6)

式中α为弹子槽螺旋角. 则由式(6)与槽深极值h可以得到倾覆偏载的评价指数C1表示为

(7)

2.2.2弹子的切向分力的合力对装置力传递的影响

由于弹子与弹子槽接触位置不同，可能导致弹子传递的径向分力的合力不为0，使装置轴向不重合而偏载，影响力的传递效果. 因此对整个弹子盘中弹子传递的切向分力的合力进行研究. 如图5所示，对图4(a)移动盘进行简化示意：圆周是弹子槽所在的位置，圆周上等间隔的分为n1个弧线区域，每个区域中都存在弹子对弹子盘的切向作用力，且弹子在该区域弧线上任一点随机出现.

则弹子对移动盘作用力向圆心处转化,表示为

(8)

式中：F3为弹子传递切向分力的合力；M3为弹子传递切向分力的合力矩；L2为弹子槽所在位置半径；n1为弹子槽个数；βi是弹子所在移动盘位置(如图5)，下标i是弹子槽编号，0≤βi≤13°,i=1,2,…,15;Fi为单个弹子对移动盘施加的切向力.

图5 移动盘切向受力简化示意图Fig. 5 Tangential force of the rectilinear motion disk

当弹子均偏向一侧时，弹子加压装置轴向不重合度最大，若n1=15，则

(9)

3 弹子加压装置的力传递效率计算

为了统一并量化弹子加压装置的力传递性能，这里构造弹子加压装置的力传递效率概念：弹子加压装置实际传递力与无摩擦、无偏载理想状态下传递力的比值称为弹子加压装置的力传递效率. 下面对弹子加压装置的力传递效率进行计算.

由引言中装置处于拟静平衡状态假设，可以建立弹子加压装置的平衡方程(如图2所示力分析)：

(10)

式中:F1为滚子对装置的轴向压力;F为装置的输出力；M为装置的加载扭矩；L3为滚子槽所在位置半径；M2为机架阻碍移动盘的力矩；φ为弹子槽摩擦角. 将式(2)(3)(9)代入(10)得

(11)

则力的传递效率为

(12)

考虑弹子槽的接触特性则需要引入修正系数C=1-C1,则：

(13)

其中C代入式(7)为

4 计算结果与分析

根据现有弹子加压装置的实值参数(如表1所示)，代入式(14)计算弹子加压装置的力传递效率. 并分析摩擦因数、摩擦角、螺旋角、弹子槽个数、驱动力等参数对该装置力传递性能的影响.

表1 参数实值

如图6所示，保持其他参数不变的情况下，改变滚珠处的摩擦因数μ2与挡边处的摩擦因数μ1得出的弹子加压装置力传递效率的等高线. 可以看出力传递效率随摩擦因数的变大而变小，当μ1为0.3、μ2为0.15时，效率低至60%以下；等高线随着摩擦因数的增大，其梯度值变小，即摩擦因数越小装置的力传递能力越不稳定；等高线对y轴的截距远远大于对x轴的截距，因此μ2对装置的力传递损失更加敏感，这是因为滚珠处结构更加接近扭矩输入端，弹子加压装置对该处损失具有放大效应. 因此在降低二者摩擦因数的同时，应着重对滚珠处接触进行优化例如增大滚珠处接触位置与转动盘几何边界距离，从而降低载荷、装配公差对接触特性的影响、减小并稳定该处摩擦因数.

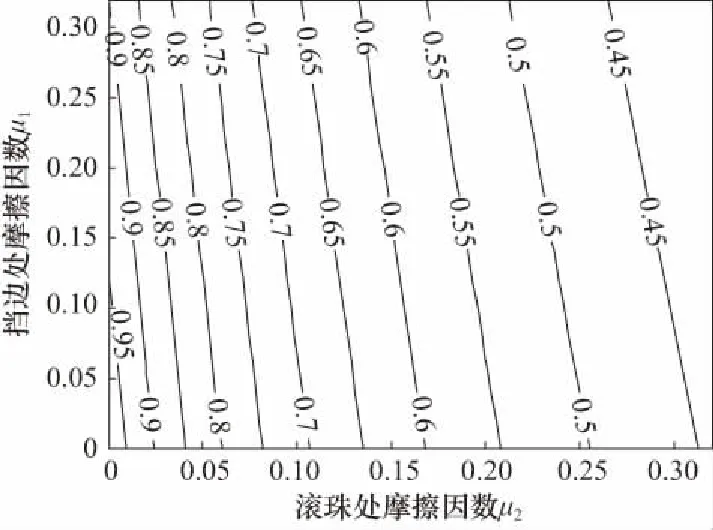
图6 摩擦因数对力传递效率影响Fig.6 Effect of friction coefficient on the force transmission ratio

如图7所示，保持其他参数不变的情况下，改变弹子槽的摩擦角φ与弹子槽的螺旋角α得到的弹子加压装置力传递效率的等高线. 可以看出该装置力传递效率存在一个极值参数，在φ为0°、α为19.88°，φ是摩擦引起的会降低装置的力传递性能，因此φ增大效率降低；当α在区间(10°,30°)上时，α越大装置力传递效率随φ增大值降低有变慢趋势. 因此改善弹子与弹子槽的润滑环境并设计弹子槽螺旋角在19.88°附近. 如果弹子与弹子槽的接触环境较恶劣可以适当增大弹子槽螺旋角来抑制效率降低.

图7 弹子槽螺旋角与摩擦角对装置效率影响Fig.7 Effect of helix angle and friction of the ball groove on force transmission ratio

如图8所示，保持其他参数不变的情况下，给出了弹子加压装置中不同部分的效率损失随滚珠处的摩擦因数μ2与挡边处的摩擦因数μ1的变化情况. 可以明显看出图8(a)中总效率损失与滚珠处损耗趋势一致，图8(b)中滚珠处损耗构成了总效率损失的主体，这与前面的滚珠处摩擦因数对装置力传递能力更敏感的分析相符合；且弹子槽处引起的轴向不重合偏载的效率损失相比与前两项很小，可以忽略.

图8 摩擦因数对力传递效率损失的影响Fig.8 Effect of the ball friction coefficient on the output load loss

如图9所示，保持其他参数不变的情况下，改变弹子槽的个数n1，得到的弹子加压装置最大轴向不重合情况. 可以看出，随着弹子槽的增多，弹子盘装置最大轴向不重合情况越严重，但是从传递同等大小载荷的情况上看无明显规律. 就选择的7种弹子槽数目结构来看，弹子槽数目为12个时偏载最轻、数目为17个时偏载最严重，但是其变化都不大于0.1个弹子传递的切向力|Fi 2|. 因此对于这7种弹子盘，弹子槽越少，装置的轴向重合度越好，但对装置的力传递性能改变不大，这与前面弹子槽处引起的轴向不重合偏载的效率损失较小相符合.

图9 弹子槽数目对装置轴向偏载的影响Fig.9 Effect of the ball groove number on the axes unbalance loading

如图10所示，保持其他参数不变的情况下，单个弹子在不同负载F2下得到的效率修正系数C. 图10(a)中F2越大，效率修正系数C越小，这是因为载荷越大弹子槽中较差的承载区域越大，更有可能造成更严重的倾覆偏载而影响装置的力传递特性；弹子槽的曲率R2增大，效率修正系数C增大，这是因为弹子与弹子槽的接触面积变小提高了接触性能. 图10(b)展示了弹子传递力与弹子槽结构的匹配情况，横轴是弹子与弹子槽的等效曲率半径R0，这是赫兹接触中的概念，横轴从小到大的过程可以认为是凸面与凸面接触向凹面与凸面接触的变化过程. 从中可以看出同等载荷接触下R0变小，传递效率修正系数C变小，这是因为接触区域越来越大，力传递能力下降的原因. 通过该图可以得出弹子结构与载荷的匹配关系，例如如果要保持弹子承载4 kN，装置传递效率修正系数大于95%，其弹子与弹子槽等效半径应小于800 mm，在不改变弹子尺寸情况下，转化为弹子槽的半径应该为12.905 mm.

图10 弹子负载对弹子-弹子槽接触副力传递的影响Fig.10 Effect of the marble load on the force transmission performance of the marbles contact pair

5 结 论

将制动器的复杂加载结构从制动器中提炼出来，使制动器的制动效能参数更具有针对性，建立了弹子加压装置的力传递计算模型，并分析摩擦因数、摩擦角、螺旋角、弹子槽个数、驱动力等参数对该装置力传递性能的影响. 得到的有意义结论如下.

① 弹子加压装置的压力输出(传递力)存在效率损失，改变装置与机架在滚珠处的摩擦特性能够高效降低力传递损失；

② 弹子加压装置弹子槽螺旋角存在最优值约19.88°，且增大螺旋角可以抑制弹子槽接触环境恶劣导致的效率损失；

③ 弹子加压装置的弹子的传力特点是：装置轴向不重合偏载较小，装置倾覆偏载较大，并可以通过图10(b)，调整弹子槽与弹子的尺寸来改善弹子的传力特性.