车辆制动器弹子盘加压机构传递函数及效率研究

张志凯，兰 海，宁克焱

(中国北方车辆研究所，北京 100072)

弹子盘加压机构结构紧凑，增力能力强，工作可靠耐用，便于与制动器集成，拆装维护方便，环境适应性好，制造成本低.特别适用于空间狭小的车辆制动、转向控制系统［1］.

弹子盘加压机构如图1所示，主要由转动压盘1、弹子2、移动压盘3、回位弹簧4、片式制动器5等零件组成.当车辆制动时，驾驶员的制动力通过作动机构作用于与转动压盘相连的拉臂上，拉臂带动转动压盘转动，通过弹子推动移动压盘向右平移，克服回位弹簧的拉力，将片式制动器压紧，从而使车辆制动.当驾驶员松开制动踏板时，作用于转动压盘上的力消失，弹子和移动压盘在回位弹簧拉力的作用下向左平移，片式制动器分离，制动力消失，车辆正常行驶.

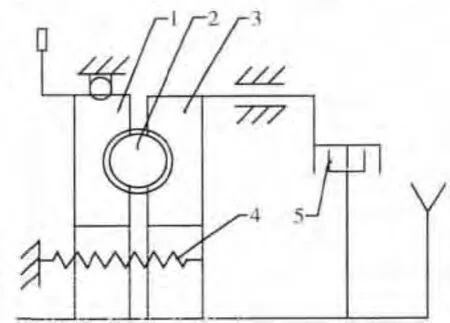
图1 弹子盘加压机构示意图

弹子盘加压机构工作的基本原理是，利用弹子在具有一定倾斜角的沟槽中滚动，在支承力的作用下，将旋转运动转化为直线运动，同时，通过压盘与弹子之间的相互挤压把作动力(矩)转变为制动器摩擦副结合的正压力，既改变了力的方向，又增大了力的大小.

本研究对弹子盘加压机构力和位移传递函数以及传动效率进行公式推导，旨在为该机构工程设计与仿真分析奠定理论基础.

1 弹子盘加压机构力传递函数推导

为便于研究，提取弹子盘加压机构结构模型，如图2所示.其中，α为转动压盘、移动压盘上弹子沟槽的倾斜角.制动过程中，弹子盘转动压盘、弹子、移动压盘受力情况如图3所示.其中，F为作用于转动压盘的作动力，Fx为沿x方向作用于转动压盘上的支撑力，Fy为沿y方向作用于移动压盘上的支撑力，Fo为移动压盘作用于制动器的压力，即弹子盘加压机构输出力，F'o则为其反作用力.图中忽略了各构件重力的影响和弹子及压盘产生的弹性变形.

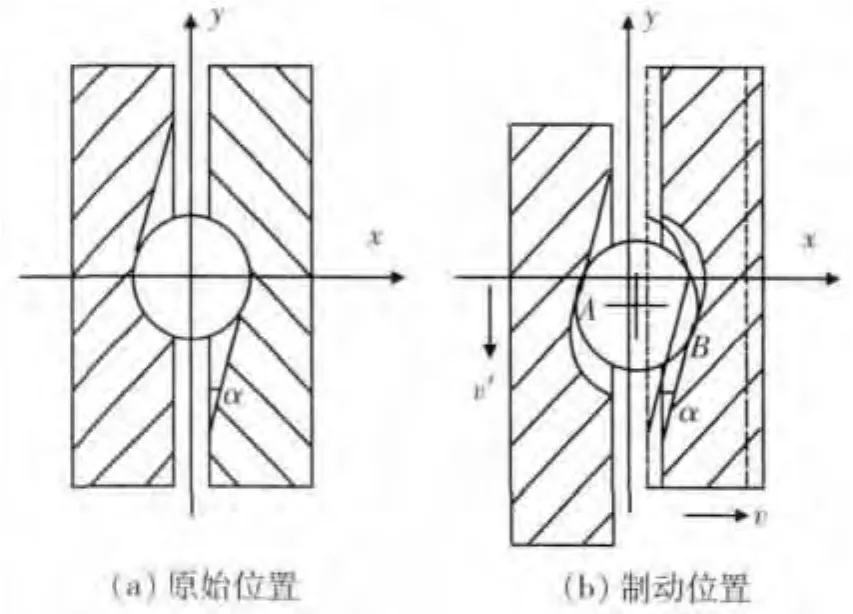
图2 弹子盘加压机构结构模型

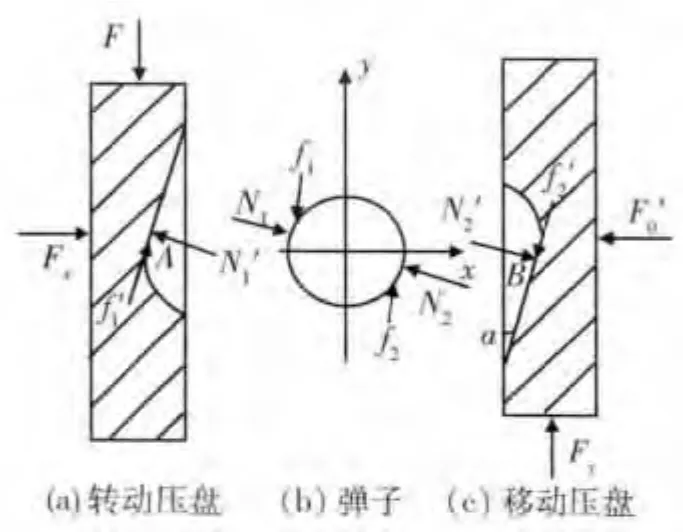
图3 弹子盘各构件受力分析

假设弹子作匀速运动，根据力的平衡关系，在y方向上，由图3(a)得:

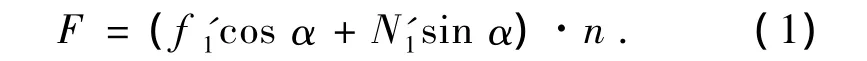
在x方向上，由图3(c)得:

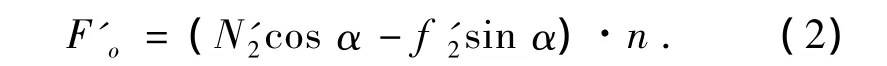
式中:n为弹子个数.

N1与 N'1、N2与N'2、f1与 f'1、f2与 f'2均为作用力与反作用力.对弹子而言，N1=N2，f1、f2为弹子受到的摩擦力.若μ为弹子与压盘间的摩擦系数，则有f1=μ·N1，f2=μ·N2.

由式(1)、式(2)得:

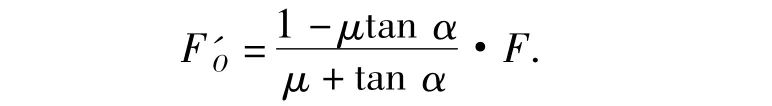
所以，弹子盘加压机构输出力为:

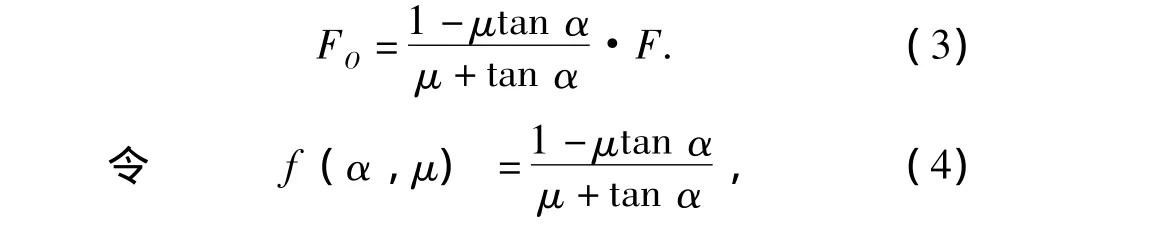
则 Fo=f(α，μ)·F .f(α，μ)即为力传递函数.

在正常状态下，力传递函数与弹子槽倾角α和弹子摩擦系数μ有关.

由式(4)分别对α、μ求导，得:

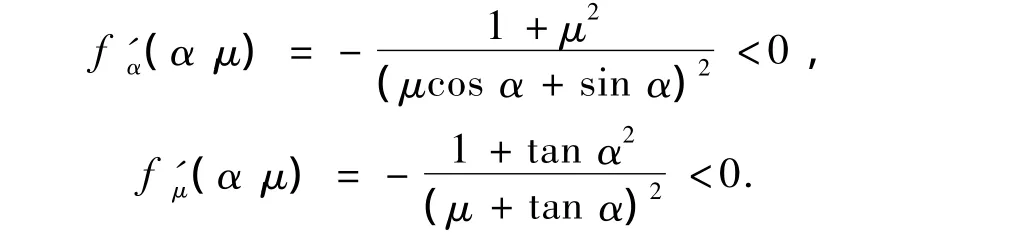
所以，力传递函数对弹子槽倾角、弹子摩擦系数而言是减函数.

因此，在工程设计中，为保证制动器摩擦副有足够大的压紧力，弹子槽倾角、弹子摩擦系数应尽可能小.减小弹子摩擦系数主要从弹子和压盘的材料、表面粗糙度、硬度、润滑等方面予以考虑.

2 弹子盘加压机构位移传递函数推导及验证

在车辆制动过程中，弹子与两压盘接触点A、B处的速度分析如图4所示.VA是弹子随转动压盘旋转的切线速度，VB是弹子随移动压盘沿轴向移动的速度.

设转动压盘旋转角度为θ(单位为度)，弹子中心线所在圆的半径为Rd，移动压盘的轴向位移为x，弹子滚动角速度为ω，则有:

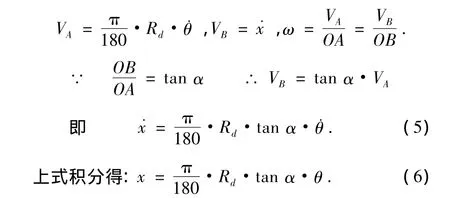
所以位移传递函数为:

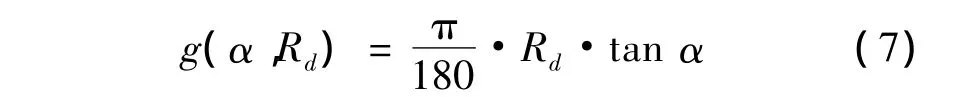
显然，g(α，Rd)随α和Rd的增大而增大.

位移传递函数的正确性得到了实物测试的验证，参见表1和图5.实物参数:Rd为185mm，α为16°，测试操纵拉臂半径为250 mm.限于测试条件，测试中记录的是弹子盘加压机构转动压盘的切向位移值，而不是转动角度，造成计算值与实测值之间存在一定的误差.

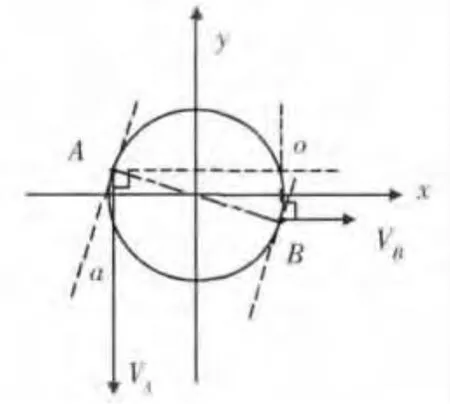
图4 弹子与压盘接触点的速度分析

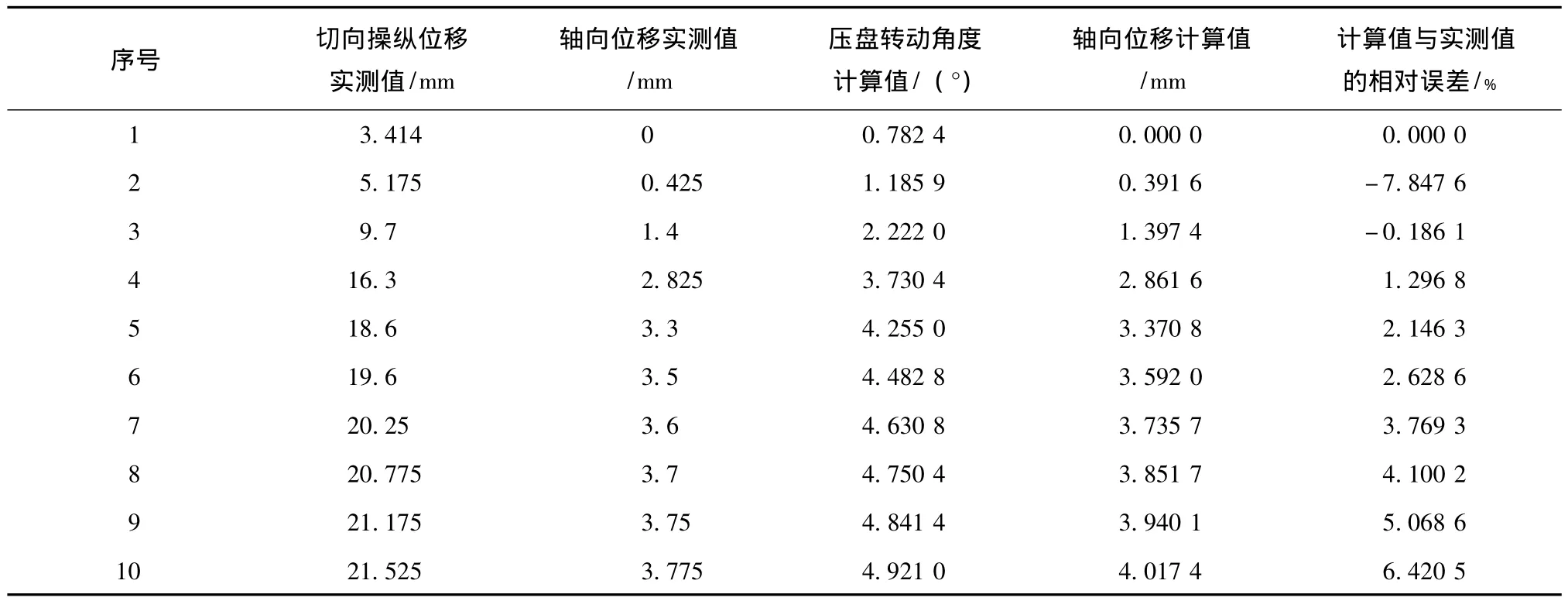
表1 轴向位移计算值与实测值

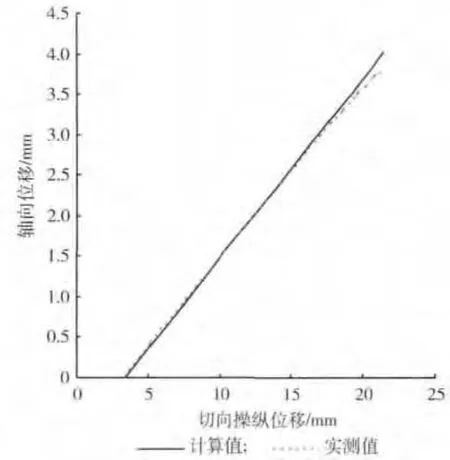
图5 位移传递计算值与实测值

3 弹子盘加压机构传动效率计算方法

图6为移动压盘在制动过程中的受力分析，图中，Fk为回位弹簧的作用力，Ff为移动压盘平移时所受的摩擦力，滑动摩擦系数为μf，产生摩擦力的正压力作用半径为Rf，Fz为作用于制动器摩擦副上的正压力，作用半径为Rz，制动器摩擦副数为m，动摩擦系数为μz，制动力矩为T.

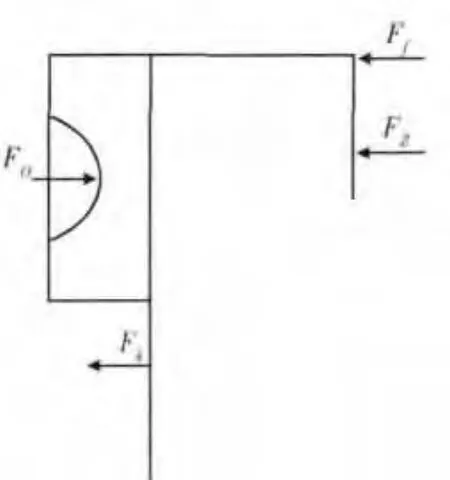
图6 移动压盘在移动方向上的受力分析

设弹子盘操纵拉臂的回转半径为R，制动拉力为Fi，则作用于转动压盘上的力为:F=，由力传递函数可得作用于移动压盘上的力为

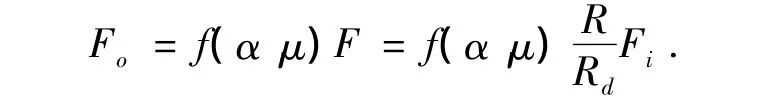
根据片式制动器工作原理有

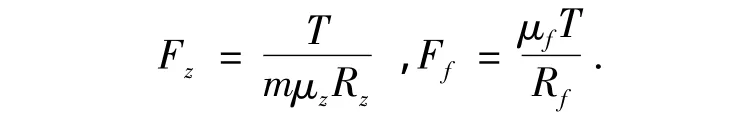
由图6知Fo=Fz+Ff+Fk，所以

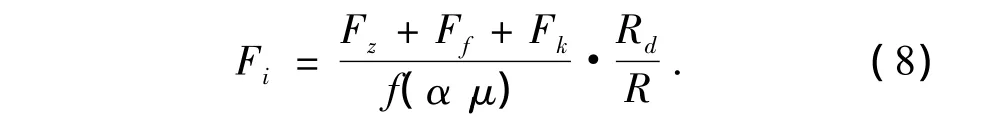
弹子盘加压机构传动效率η为:

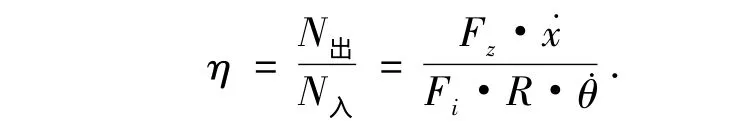
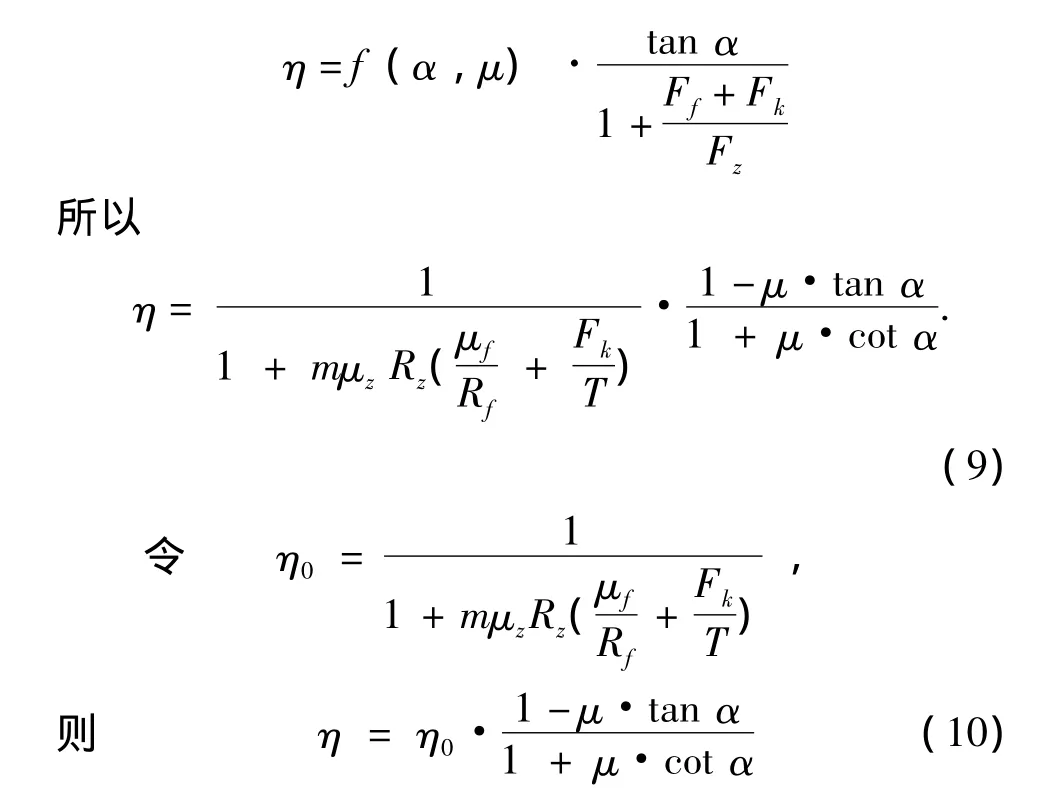
影响弹子盘加压机构传动效率因素分析:

在工程设计中，根据车辆制动性能要求确定制动器制动力矩的大小，进而确定制动器摩擦副数及结构，移动压盘摩擦系数和尺寸也会根据零件的材质和结构加以确定.因此，影响传动效率的因素有3个，即回位弹簧拉力Fk、弹子摩擦系数μ及弹子槽倾角α.

1)回位弹簧拉力Fk对效率η的影响.由式(9)可知，η随Fk的增大而减小，因此，设计时，在保证移动压盘快速回位，即保证制动器摩擦元件快速分离的前提下，应尽可能取较小值.

2)弹子摩擦系数μ对效率η的影响.对式(10)关于μ求导得:

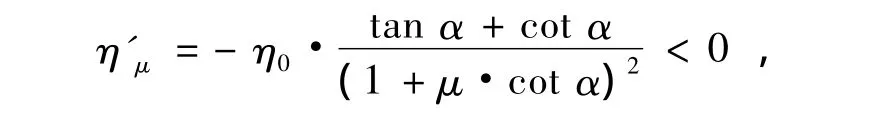
所以，η随μ的增大而减小.在实际使用过程中，由于磨损的累积和挤压变形，弹子摩擦系数不断增大，将使弹子盘加压机构的传动效率不断下降.

3)弹子槽倾角α对效率η的影响.对式(10)关于α求导得:

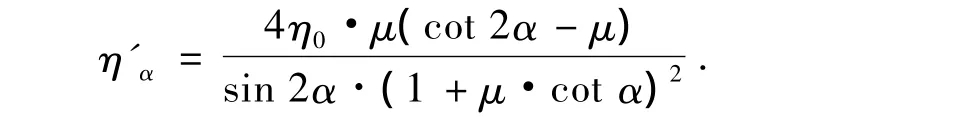
4 应用实例

某车辆制动系统弹子盘加压机构及片式制动器有关参数如下:弹子和压盘材料均为钢，弹子摩擦系数μ=0.003，弹子槽倾角α=16°，拉臂回转半径R=524 mm，弹子中心所在圆(滚道)半径Rd=370 mm，滑动摩擦系数μf=0.18，正压力作用半径Rf=0.23 m，摩擦副数m=4，摩擦片动摩擦系数μz=0.26，摩擦副正压力作用半径Rz=0.185 m，回位弹簧拉力Fk=2 kN，制动力矩T=10.16 kN·m.试计算该弹子盘加压机构的力放大倍数、压盘位移与操纵拉臂角位移的转换关系以及传动效率.

由力传递函数关系式(4)得弹子盘加压机构力的放大倍数为:

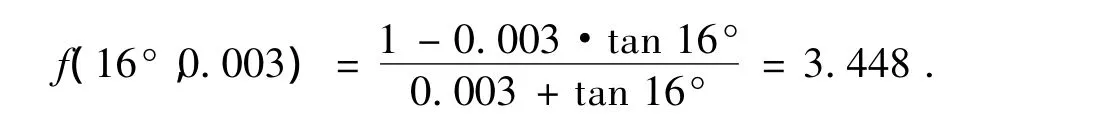
由位移传递函数关系式(6)得制动器压盘位移x与弹子盘操纵拉臂转角θ的关系为:

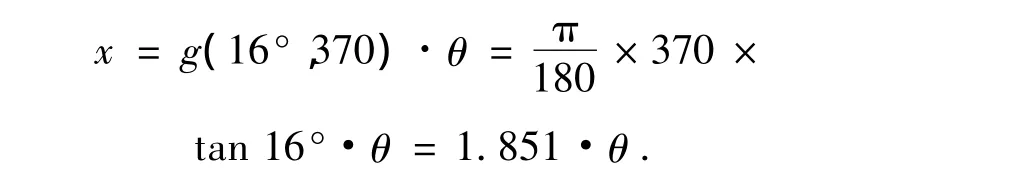
由传动效率计算式(9)得弹子盘加压机构的传动效率为:

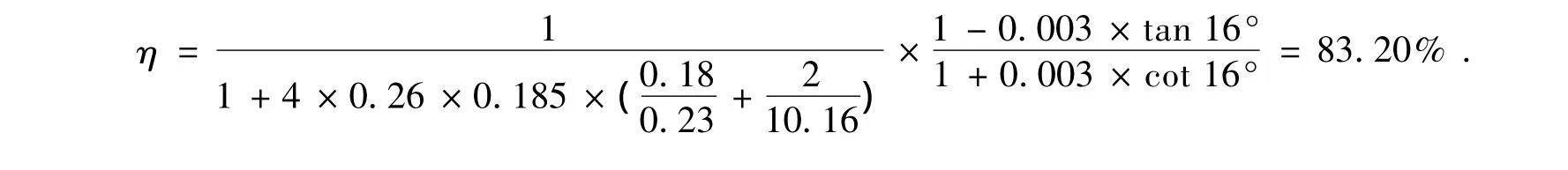
5 结论

通过对弹子盘加压机构受力及速度分析，推导出了该机构力和位移的传递函数，提出了传动效率的计算方法，并对有关影响因素进行了分析，研究结果可以应用于弹子盘加压机构的工程设计和仿真分析.从上述计算式得出如下结论:

1)弹子盘加压机构力的放大倍数随弹子槽倾角、弹子摩擦系数的增大而减小，位移传递量随弹子槽倾角增大而增大.

2)弹子盘加压机构的传动效率随弹子槽倾角增大而提高，随弹子摩擦系数、回位弹簧拉力的增大而降低.

3)弹子及其压盘上的弹子槽应进行硬化处理，接触表面应保证具有较高的粗糙度，以实现较低的滚动阻力，保证力的放大效果，同时，有助于提高传动效率.

4)弹子槽倾角的确定应综合考虑力的放大倍数、移动压盘最大行程和传动效率等实际工程要求.

5)弹子盘加压机构中回位弹簧的拉力要适度，设计时应根据驾驶员施加在制动踏板上的力的大小、弹子盘增力倍数、压盘回位阻力等因素加以确定.

［1］张洪图，姜正根，赵家象.坦克构造学 ［M］.北京:北京工业学院出版社，1986.