基于kmeans-SVM的二叉树粗分类方法∗

（北京细推科技有限公司 北京 100026）

1 引言

随着信息技术的发展，需要处理的数据量也越来越大，如何能更有效地获得想要的信息是人们越来越关注的问题，其中常用的办法就是对数据做粗分类处理，根据数据的某些特征把数据粗分为若干类，再根据想要信息的特征去相应的类别里面去查找，这样不仅缩小了搜索范围提高了搜索效率，还明显节省了时间。

生物识别技术主要是根据人体固有的生理特性和行为特性等生物特征进行身份认证的一种技术，现在生物识别技术已经应用于生活的各个方面，如指纹、人脸、静脉、虹膜等。

以人脸识别为例，当1：n识别时，即从成千上万的人脸中找出目标人脸，如果n比较大的情况下算法的时间复杂度比较高，因此需要缩小搜索范围，提高算法的运行效率，因此有必要对数据做粗分类处理。

常用的分类方法：k-means［1］、支持向量机［2～7］（Support Vector Machine，SVM）、Kdtree［8～9］、集成分类器［10～12］、贝叶斯分类［13～14］等。k-means［1］算法是一种基于样本间相似性度量的间接聚类方法，属于非监督学习方法，实现起来比较简单。此算法以k为参数，把n个对象分为k个簇，以使簇内具有较高的相似度而紧密的联系在一起，而且使得簇间的相似度较低而距离尽量的大。但是k-means［1］是局部最优的，而且容易受到初始质心的影响。支持向量机［2～7］（Support Vector Machine，SVM）是在特征空间里寻找一个最大间隔超平面，在这个最大间隔超平面的两边建立两个互相平行的超平面，这两个平行超平面间的距离越大，分类器的总误差越小。SVM［2～7］在解决非线性以及高维模式识别问题中有许多特有的优势。但是SVM［2～7］属于有监督学习，使用SVM［2～7］训练之前需要先做粗分类好训练数据。Kdtree［8～9］是k-dimensional tree的缩写，是一种高维索引树形数据结构，常用于最近邻查找（Near⁃est Neighbor）和近似最近邻查找（Approximate Near⁃est Neighbor），因此可以用来做粗分类，缩小目标的搜索范围，但是Kdtree［8～9］做粗分类的话一般拿各类数据的类中心来训练树形结构。集成分类器［10～12］是指把性能较低的多种弱学习器，通过适当组合形成高性能的强学习器的方法，通常采用Bagging和Boosting的方差去训练单个弱分类器，然后通过投票的方式做最终的决策，集成分类器取得了很好的分类效果。贝叶斯分类［13～14］是一类利用概率统计知识进行分类的一种统计学分类方法。

2 基于kmeans-SVM的树粗分类

本文提出一种结合k-means［1］和SVM［2～7］的一种树形粗分类方法，利用k-means［1］提供的无监督分类结果作为训练SVM［2～7］的训练数据，然后在根据SVM［2～7］的预测结果不断调分割超平面，最后形成二叉树型分类树。

首先用k-means［1］算法得到用以训练粗分类分类器的训练数据。假设样本数据集D={x1,x2,…,xn}，以及数据集D对应的标签Y={y1,y2,…,yn}，其中yi∈{-1,1} 。聚类的簇数k，簇划分C={c1,c2,…,ck}，从数据D中随机选择k个样本作为初始的k个质心，计算数据D中的任意样本xi(i∈[1,n])距离各个质心cj(j∈[1,k])的距离，把xi划分到距离最小的质心所在的簇，当D中所有样本划分完后各自重新计算k簇的k个质心，然后根据新的k个质心重新划分数据D，重复更新质心直到质心不在发生变化为止。这样就得到了训练SVM［2～7］的k类数据C={c1,c2,…,ck}。

其次用SVM［2～7］在特征空间中找到一个最优分类超平面wT⋅x+b=0把数据C={c1,c2,…,ck}分开，要找到这个最优平面，需要求解如下二次规划问题：

满足：

利用拉格朗日法把上述二次优化问题转化为其对偶问题：

求解对偶问题得到原二次规划问题的解，最终得到最优分类超平面。

k-means［1］聚类算法是无监督的分类算法，此算法分类时根据样本距离簇中心点的距离来划分类别，当样本位于两簇的连接地带时，同一类别的样本可能被错误地分到了不同的簇里面，我们可以用聚类得到的两簇有“标签”的数据去训练一个SVM［2～7］分类超平面，然后根据超平面去调整两簇有“标签”的数据，用新得到的两簇有“标签”的数据再训练一个新的分类超平面，以此迭代不断更新两个有“标签”的簇和分类超平面，直到有“标签”的簇和分类超平面不在变化则停止迭代。最后根据最终的分类超平面把数据分割成两部分，这两部分数据分别作为新节点的训练数据。

利用k-means［1］无监督学习的特点，根据特征空间中的欧式距离把相近数据聚成若干簇。k-means［1］把特征数据分成两类，分别标记为0和1，接下来根据这两簇有标签的数据训练一个SVM［2～7］的二分类器，找到一个平面把尽可能多的0和1分别分割在一个平面的两侧，SVM［2～7］训练完成以后拿训练好的平面测试k-means［1］聚类得到的两类数据，把SVM［2～7］预测准确的数据拿来重新训练SVM［2～7］的分割平面，照此方法迭代更新SVM［2～7］的分割平面直到用SVM［2-7］预测数据的误差个数不在发生变化为止。根据最后得到的SVM［2～7］分割平面把k-means［1］得到的两类数据中SVM［2～7］能分类正确的数据分别是左右两个子节点的训练数据，把SVM［2～7］分类错误的数据同时属于两个子节点的训练数据。并且在每个节点都要保存该节点数据的所有类别数据的中心点（同类数据求和算平均值），每一类中心点数据在做预测knn［15～16］搜索时使用。

预测的时候指定knn［15～16］的范围，使用knn［15～16］算法根据每个节点数据中每一类的中心点数据返回预测数据距离这些中心点最近的前若干（预测时需要提前指定）结果。

3 算法流程

1）在根节点用k-means［1］聚类算法把数据聚成两簇，分别标记为0和1。

2）利用步骤1）得到的两类数据去训练一个SVM［2～7］的分类器，再用得到的SVM［2～7］分类器去分类训练数据，根据结果重新划分0和1数据集里的数据，接下来用得到的新0和1数据集训练新的SVM［2～7］分类器；重复以上过程直到0和1数据集不在发生变化时则停止训练。

3）由步骤2）中得到的0和1两个数据集，在根据样本的实际标签，若同一类中的数据被完全划分到0或者1中，则这类样本不做处理；若同一类中的数据既有一部分划分到了0中，又有一部分数据划分到了1中，则这类数据的全部数据既要放入0中，又要放入1中。

4）以步骤3）中最终划分得到的0和1数据分别为新的父节点，执行步骤1）、2）、3），直到满足二叉树的终止生长条件。

5）预测时指定knn［15～16］的搜索范围，根据每个候选节点上标签信息以及中心点完成粗分类预测。

流程图如图1。

图1 算法流程图

4 实验及分析

实验以人脸分类为例，实验中采样LFW人脸数据库，LFW数据集中一共包含5000个人脸数据，数据集中的人脸大多是在非限制环境下拍摄的，数据集包含13000多张人脸图像。

本实验每个人脸图片提取一个1024维度的特征向量。其中训练数据49686个样本，测试数据24830个样本。对比方法是kdtree［8～9］中提到的算法，其中训练kdtree［8～9］时使用每类特征的中心点作为训练数据。实验分别测试了在测试集中搜索范围前200、300、400和500条件下的准确率。

实验结果如表1。

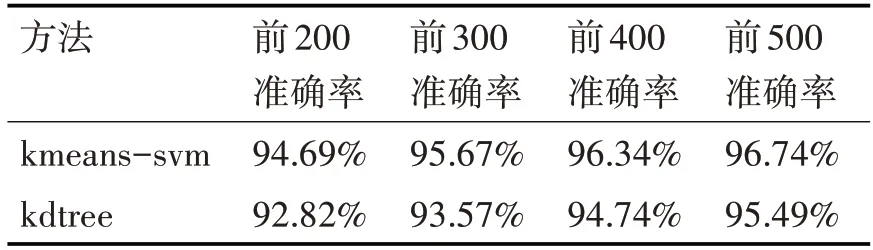
表1 实验对比结果

从表1的实验结果可以看出本文提出的方法优于kdtree［8～9］方法。

5 结语

针对大数据范围搜索时可以使用粗分类方法，缩小目标的搜索范围，本文方法的优点在于将易分错数据分别加入左右子树的训练数据中去训练新的节点，从而一定程度上避免了误差累计，增加了识别准确率，在利用树形结构的优点对数据集进行拆分很好地达到了缩小搜索范围的目的，提高了搜索效率。