基于改进的BPSO算法的关联规则挖掘

（江南大学 无锡 214122）

1 引言

关联规则指数据库中超过指定最小支持度和最小置信度的项目的集合，作为数据挖掘的重要组成部分它一直是学者的研究热点［1］。随着挖掘问题变得越来越复杂，诸如Apriori算法与FP-growth算法等传统算法出现了缺点，其中最典型的是由大量候选项集和复杂的数据结构所造成的时间和内存的成本，导致挖掘效率较低［2］。因此许多学者开始使用启发式算法，粒子群优化算法（PSO）是应用较为广泛的算法之一［3］。

有许多研究将启发式算法应用于关联规则挖掘。例如，Chen等使用PSO算法从高维数据集中挖掘关联规则［4］，Rom提出的基于遗传算法的关联规则可避免挖掘过程中发现的无用个体［5］，BADA等融合了PSO算法和蚁群算法（ACO），将事务数据转换为二进制数据后，从数据集中挖掘频繁项集［6］，Kuo等使用PSO算法快速有效计算出关联规则的最小支持和置信度［7］。

然而，大多数改进的PSO算法重点考虑粒子全局和局部搜索能力，而忽略了粒子种群和搜索范围带来的影响。因此，本文提出了一种改进的二进制粒子群优化算法（GRBPSO），根据适应度函数对粒子初始种群进行预处理，并以频繁项集的性质为依据对粒子搜索空间进行缩减，减少算法运行时间。

2 基本概念

2.1 频繁项集

频繁项集的有关定义为I={i1,i2,…,im}是m个不同项目的集合，每个ik称为一个项目［8］。数据集D={t1,t2,…,tn}是n个不同事务的集合，每个tk称为一个事务，其中tk⊆I。集合X⊆I称为项集，|X|表示项集中的项目数，长度为1的项集称为1项集。项集X的支持度表示为sup（X），其含义是项集X在数据集D中出现的实际频率，若sup(X)≥最小支持度(min_sup)，则称项集X是频繁项集。

频繁项集挖掘的目标是根据给定的最小支持度（min_sup）挖掘出所有的频繁项集。根据以上描述，可推出性质1。如下所示：

性质1：∀Xi⊆X⇒sup(Xi)≥sup(X)

因此，当Xi⊆X时，若Xi不是k维频繁项集的子集，则项集X也不是k维频繁项集的子集。

2.2 关联规则

关联规则是形如A⇒B的蕴含式［10］，其中A⊂I，B⊂I，并且A∩B=∅。

一般使用三个指标来度量关联规则，分别是支持度（support）、置信度（confidence）和提升度（lift）［11］。根据这三个指标可以筛选出满足条件的关联规则。

以A⇒B这个关联规则为例来说明：

支持度（support）：表示同时使用A、B的人数占所有用户数的比例。如果用P（A）表示使用A的用户比例，那么support=P（A&B）。

置信度（confidence）：表示使用A的用户中同时使用B的比例，即同时使用A和B的人占使用A的人的比例，即confidence=P（A&B）/P（A）。

提升度（lift）：表示“使用A的用户中同时使用B的比例”与“使用B的用户比例”的比值，即：lift=（P（A&B）/P（A））/P（B），提升度反映了关联规则中的A与B的相关性，提升度大于1且越高表明正相关性越高，提升度小于1且越低表明负相关性越高，提升度=1表明没有相关性［12］。

2.3 二进制粒子群优化算法（BPSO）

PSO算法在实现过程中随机选取一群粒子作为初始粒子群，搜索空间中的每个粒子都是一个可能解，算法通过迭代找到最优解。在算法迭代过程中粒子以两个极值为依据来更新自己，第一个极值称为个体极值，是粒子个体找到的最优解；第二个极值称为全局极值，是整个种群目前找到的最优解。

离散二进制粒子群算法是J.Kennedy和R.C.Eberhart在1997年提出的［13］。PSO算法设计之初是为了优化连续函数的，但实际生活中待解决的问题大多是基于离散空间上的组合优化问题，因此提出BPSO算法以解决这一问题。

BPSO算法在离散粒子群算法基础上，约定位置向量、速度向量均由0、1值构成［14］。粒子根据式（1）更新自己的速度，根据式（2）和式（3）更新自己的位置，式（2）为映射函数：

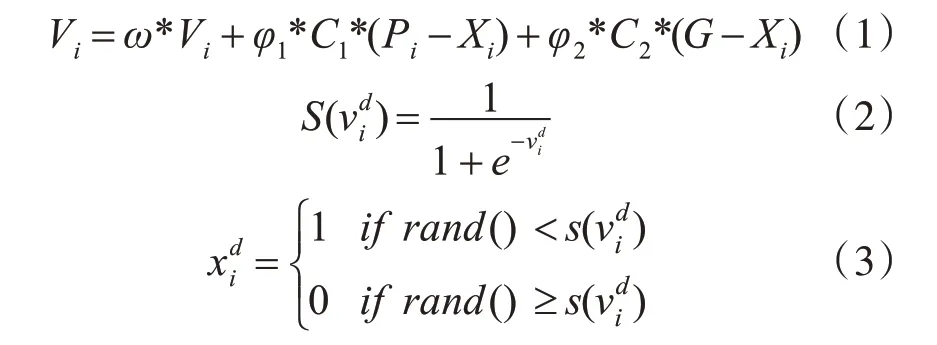
其中，Vi为第i粒子的速度，pi为个体极值，G为全局极值，ω为惯性因子，C1,C2为学习因子，φ1和φ2为［0，1］之间的随机数。为在d维空间中第i个粒子轨迹当前为0的概率，为在d维空间中第i个粒子位置变化的绝对概率，rand（）为［0，1］之间的随机数。

3 GRBPSO算法

3.1 适应度函数

适应度函数是用来评价给出的候选解即粒子的好坏的［15］。在PSO算法中，适应度函数往往具有驱动粒子前进的作用，在搜索空间中指出粒子的前进趋势。适应度函数的设计依赖于实际问题，针对不同问题，适应度函数的设计也不尽相同。

在关联规则的研究中支持度是评价一组关联规则是否有效的基础指标。支持度代表了项目重复出现在一组事务数据库中的次数。现实中数据库内的数据往往具有多样性和复杂性，为了在实际项目中挖掘有意义的关联规则，本文算法将粒子出现的实际次数作为其适应度值，粒子的适应度函数如式（4）所示：

其中，support(i)为粒子种群中粒子的实际支持度也即实际出现频率。

在GRBPSO算法中，个体极值指的是粒子群中各个粒子在此次迭代条件下的支持度，全局极值指的是在此次迭代条件下整个种群中全部粒子的最优支持度，算法在每次迭代中修改这两个极值，假设某个粒子的个体极值不小于最小支持度，则将该粒子列为候选项集。

3.2 初始粒子群预处理

在频繁项集挖掘过程中数据集中可能存在某些项目出现频率较低的现象，这就可能导致随机选取的粒子种群质量不高，进而影响挖掘结果及挖掘效率。在GRBPSO算法中，首先对初始粒子群进行预处理，保证一定比例的粒子具有合理的初始适应度。

对初始粒子群进行预处理的方式是将种群中出现频率较低的粒子位置设置为0，首先以确保初始粒子群具有适当的适应度，提高初始种群的质量；同时在二进制数据集中也可减少粒子的数量和空间维数。在GRBPSO算法中，结合关联规则的相关定义，可根据用户设置的最小支持度值修改对应粒子的位置值，修改方式为若粒子的出现频率即初始适应度值小于最小支持度，则将该粒子的位置更新为0。

3.3 缩减搜索空间

利用BPSO算法在大数据集中挖掘关联规则意味着搜索空间较大，而搜索空间对算法运行效率有着重要的影响，因此，本文设计一种缩减搜索空间的优化策略，减少搜索空间，提高算法运行效率。

假设GRBPSO算法在发现频繁项集阶段，G为当前全局极值。在此期间，任一支持度小于G的项目将会被剪枝，即∀i∈I，若sup(i)＜sup(G)，则项目i被剪枝。于是，∀i∈I且sup(i)＜sup(G)，从性质1可知，∀X⊂I且i∈X，可推出sup(X)＜sup(G) 。也就是说，若项集中含项目i，则需更新该项集，将其中的项目i剪枝。

4 实验及分析

为了验证GRBPSO算法的正确性及有效性，本文对大量数据集进行了实验，并给出在6个数据集上的实验结果及分析比较。实验环境为2.10GHz AMD R5 CPU，8G内存和Windows 10操作系统，算法在VS2015平台上采用C++语言编程实现。数据集分别为Connect、Mushroom、Retail、Pumsb、Ko⁃sarak、BMS-POS，数据集下载地址为http：//fimi.uantwerpen.be/data/。数据集展示如表1所示。

表1 实验数据集

4.1 实验一

在实验一中，从种群规模方面对GRBPSO算法与BPSO算法进行比较。算法的参数设置为最大迭代次数N=10，惯性因子ω=0.2，学习因子C1=C2=1，粒子最大速度为2。算法中的最小支持度设置为0.3，最小置信度（min_conf）设置为0.6，最小提升度（lift）设置为4。实验结果如图1所示。

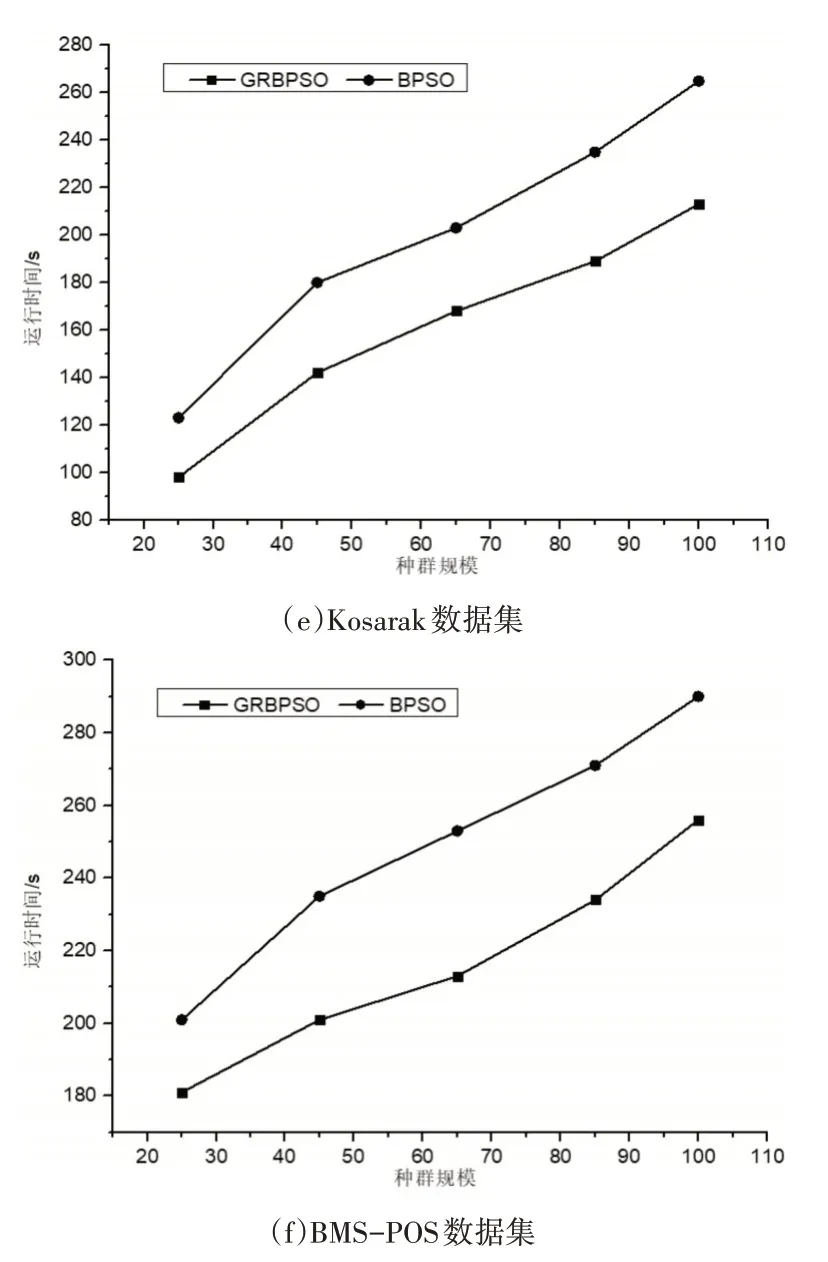
图1 算法运行时间对比

图1表示在种群规模为可变因素的情况下两种算法在6个数据集上挖掘关联规则的时间对比。由图1可知，两个算法在种群规模不断增加的情况下，运行时间也随之增加，原因是种群规模的扩大导致算法中对适应度的计算变得复杂，进而影响算法的运行时间。但由图1可知本文算法的运行时间始终小于BPSO算法，并随着规模变大这种优势愈加明显，因此充分说明本文算法在种群规模变化的前提下是高效的。

4.2 实验二

在实验二中，从迭代次数上对GRBPSO算法与BPSO算法进行比较。算法的参数设置为种群规模K=80，惯性因子ω=0.2，学习因子C1=C2=1，粒子最大速度为2。算法中的最小支持度设置为0.3，最小置信度（min_conf）设置为0.6，最小提升度（lift）设置为4。实验结果如图2所示。

图2表示在迭代次数为可变因素的情况下两种算法在6个数据集上挖掘关联规则的时间对比。由图2可知，两个算法在迭代次数的不断增加下，运行时间也随之增加，并由图2可知本文算法的运行时间始终小于BPSO算法，并随着迭代次数的变多在部分数据集中这种优势愈加明显，因此充分说明本文算法在迭代次数变化的前提下是相对高效的。这是因为大数据集导致搜索空间变大，GRBPSO算法在对初始种群进行预处理时可一定程度地缩减搜索空间，并同时采用了优化策略对搜索空间进行裁剪，大大减少粒子的飞行空间，在一定程度上提高了关联规则挖掘效率。

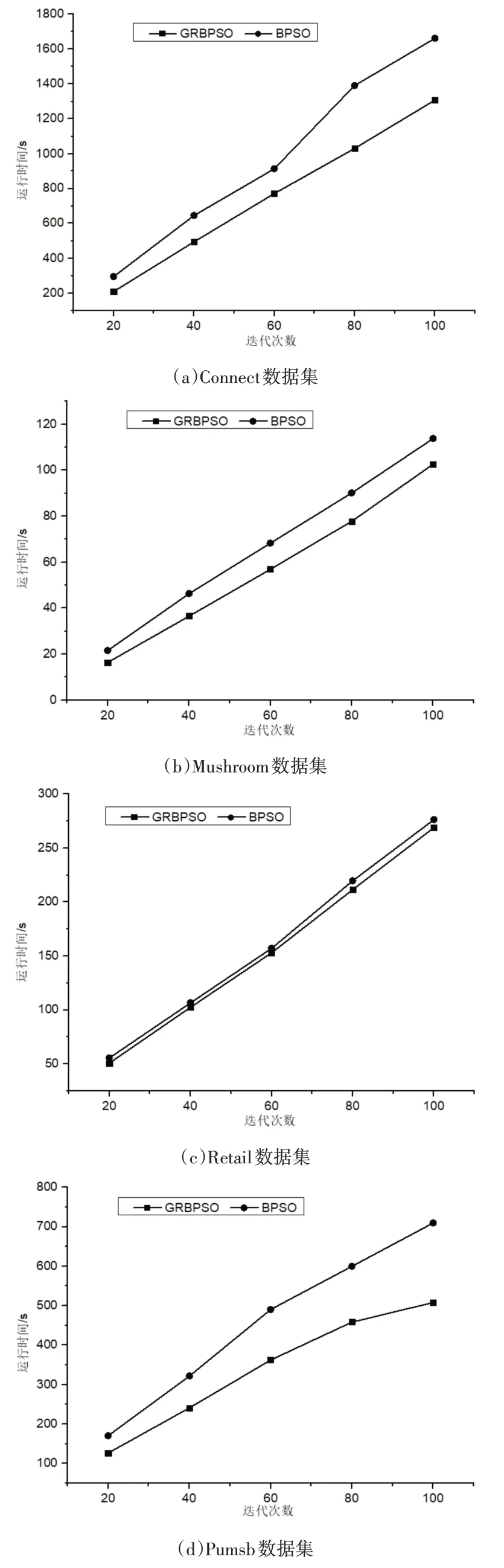
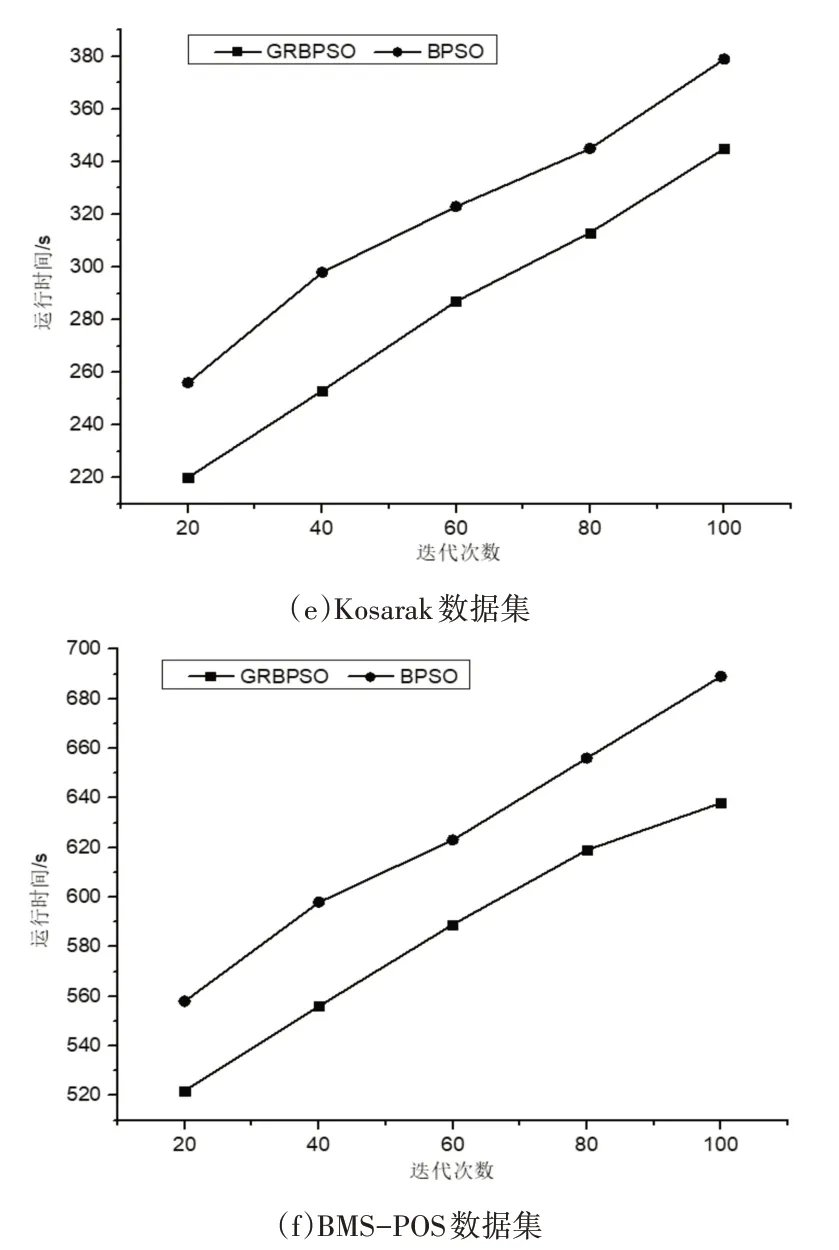
图2 算法运行时间对比

4.3 实验三

在实验三中，比较GRBPSO算法与同类型算法的挖掘效果。本文以挖掘频繁项集的数量作为参考值，同类型算法分别为PSOFIM算法［16］、GA-Apriori算法及PSO-Apriori算法［17］。根据文献［17］，表2中的对比算法均为在最优参数下算法挖掘的数量，本文算法的挖掘结果具有不确定性，原因是算法在初始种群的选择上具有随机性。为说明本文算法的可行性和稳定性，本次实验在6个数据集中均重复10次，实验的最终数据为10次实验的平均结果。算法的参数设置为种群规模K=80，迭代次数N=20，惯性因子ω=0.4，C1=C2=1，Vmax=3，算法的最小支持度均为0.2，实验对比结果如表2所示。

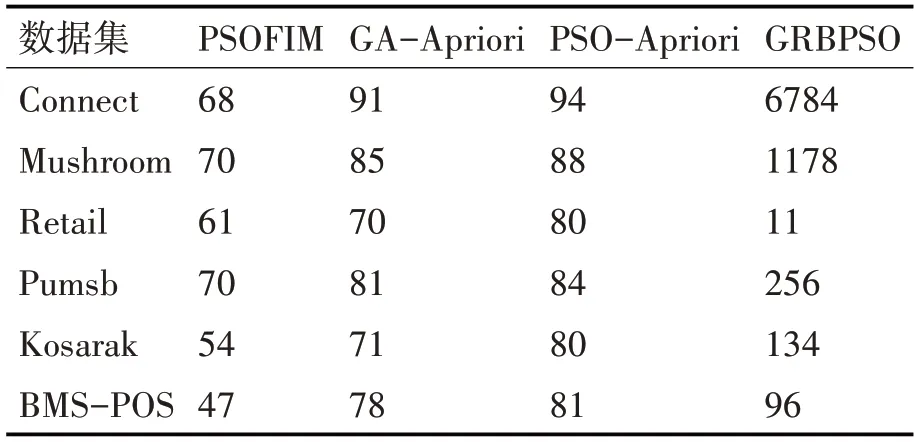
表2 各算法挖掘到的频繁项集数量（/个）

由表2可知，以数据集Retail为例本文算法的频繁项集挖掘数量少于其他同类型的3个算法，但在其他数据集中本文算法表现较为优越，尤其是在Connect数据集和Mushroom数据集中表现突出。在Retail数据集中本文算法挖掘数量少于其他3种算法是由Retail数据集的特征引起的，在Retail数据集中事务数据库的平均长度较小且数据分布较为零散，数据集中事务属性数较少，在进行频繁项集挖掘时本文算法对初始粒子群的选择是具有概率性的，因此在预处理过程中粒子位置为0的概率变大，导致挖掘结果不佳。但从整体来看，本文算法在大数据上挖掘频繁项集是可行的，并且挖掘结果也是可观的。

5 结语

本文提出了一种基于改进的二进制粒子群优化算法的关联规则挖掘方法。首先结合实际情况，将粒子支持度作为GRBPSO算法的适应度函数；然后根据最小支持度对初始种群进行处理，提高初始种群质量；最后根据优化策略对搜索空间进行缩减。通过实验证明，本文提出的GRBPSO算法在挖掘关联规则上是可行的且高效的。