基于改进相似度计算方法的协同过滤算法研究∗
2021-04-04
(江苏科技大学计算机学院 镇江 212003)
1 引言
伴随着互联网和信息技术的快速发展,数据量呈指数型增长,在促进社会经济快速发展的同时,也使我们面临着严重的“信息过载”问题[1]。如在电子商务领域,面对海量商品,买家容易产生选择疲惫,从而会使商家失去宝贵的潜在客户资源。推荐系统基于用户历史数据记录,根据相关算法处理用户数据,完成个性化商品推荐,使用户能够快速并准确地获取自己感兴趣的商品。目前,推荐系统已经广泛应用在电子商务、电影推荐、新闻推荐、音乐推荐、短视频推荐等领域[2]。协同过滤是目前推荐系统中使用最广泛也是最成熟的一种推荐算法[3],分为基于用户的协同过滤(User-based CF)和基于项目的协同过滤(Item-based CF),它们都是基于邻域的推荐[4]。协同过滤主要分为三个步骤:用户-项目评分矩阵的建立、相似度计算、评分预测。其中相似度计算是最核心的部分,后续的评分预测是在此基础上完成的,相似度的计算将直接决定着推荐系统的质量[5]。本文是在基于用户的协同过滤基础上,对相似度的计算加以改进的。
2 传统协同过滤算法
基于用户的协同过滤的算法思想是通过计算用户间的相似度,找到目标用户的相似邻居集,通过分析相似用户对某些商品的评分数据,来预测目标用户的未评分项目的分值,选取评分最高的若干项目进行推荐[6]。传统相似度计算方法主要有余弦相似度、皮尔逊相似度、杰卡德相似度等[7]。
2.1 余弦相似度
余弦相似度是将用户对项目的评分看成两个空间向量[8],通过计算两向量的余弦值,来衡量用户间相似度大小,余弦值越大,两向量之间夹角越小,相似度越高。余弦相似度只考虑夹角大小,仅在角度这个维度上去比较相似度。
余弦相似度计算公式:

2.2 皮尔逊相关系数
皮尔逊(Pearson)相似度又称相关相似度,是基于两用户共同评分项目来计算两向量线性相关程度的一种统计计算方法[9]。计算结果值介于-1和1之间,当值为负数时,表示两向量负相关,为正数则呈正相关,值越接近上下限,两向量线性关系越强。
皮尔逊相关系数计算公式如下:
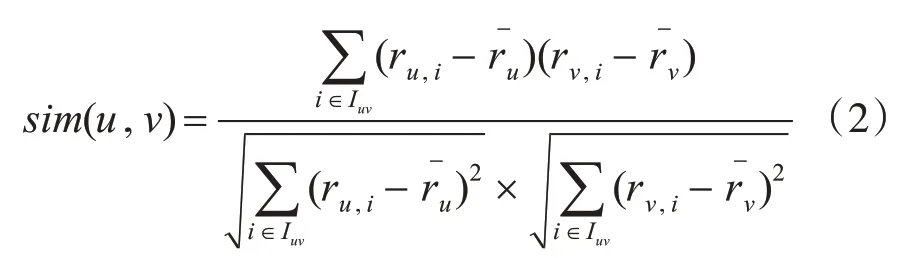
rv,i表示用户v对项目i的评分,为用户v的平均评分。
2.3 杰卡德相似度
杰卡德相似度是从集合的角度去考虑,即两用户共同评价项目数占两用户总的评价项目的比例[10]。该相似度计算方法只注重是否被用户评价,而忽略具体评分的影响,一般用于离散型二元变量(喜欢、不喜欢;点赞、踩等),对于非二元变量的使用场景,计算效果较差。
杰卡德公式如下:
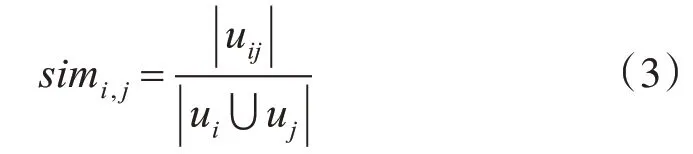
Ui,j表示用户共同评价的项目,Ui表示用户对项目i的评分。
根据相关研究文献,Pearson相似度计算的实验效果较其余方法准确率更高[3],故本文的相似度计算的改进以Pearson相似度为基础。
3 协同过滤算法的改进
随着系统中用户数和商品数的指数型增长,用户的评分数据显得十分稀疏,这会对相似性计算的准确性产生很大影响。近年来,很多学者对相似度的计算提出了改进,李容等[11]提出了共同评分项目数占比来改进相似度的计算,文俊浩等[12]提出Tan⁃imoto修正系数,并将用户共同评分项和用户所有评分项之间的关系融入到传统的相似性计算方法中,这些算法的改进在一定程度上提高了相似度计算的准确性,但依然存有一些缺陷。
3.1 用户的平均评分对相似度计算的影响
传统的Pearson相似计算并没有考虑到每个用户的平均评分情况,只是单纯地直接计算向量间的线性关系[13]。如表1,表示用户和对应项目的评分,用评分向量表示用户,U1=(2,1,2,1,1)和U2=(5,4,5,4,4),利用Pearson相似度计算可得出sim(U1,U2)=1。而实际上,两用户在对应项目上评分悬殊很大,根据具体评分可以看出,U2用户对项目1和2比较喜欢,而用户U1明显不太喜欢这两个项目,说明两用户间相似性并不大,而通过皮尔逊相似度公式计算的相似度却为1,现实情况与传统的Pearson相似度计算结果相冲突。
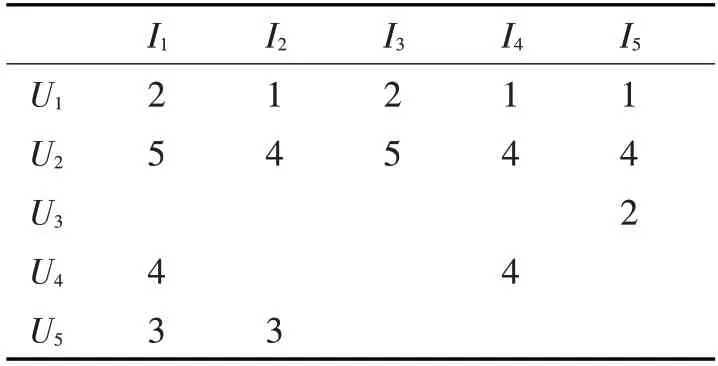
表1 用户-项目评分矩阵
为了解决这个问题,本文提出平均评分修正因子,以衡量用户间的评分差异,公式如下:
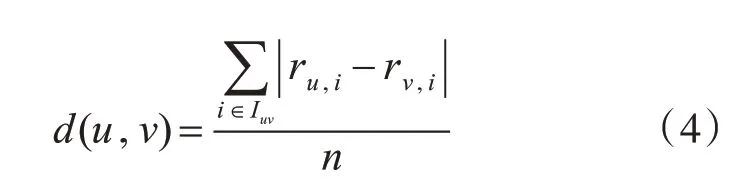
d(u,v)表示两向量的欧氏距离[14],n为两用户共同评分项的数量,ru,i和rv,i分别表示两用户对同一商品i的评分,d(u,v)值越小,两用户间评分差距越小,相似度越高,则平均评分修正因子如下所示:
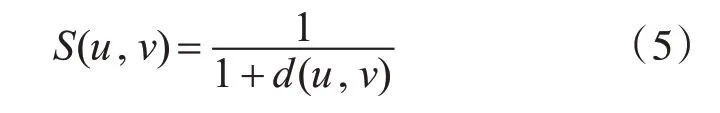
很明显,d(u,v)越小,S(u,v)值越大,用户间相似度越高。
3.2 商品的热门程度对相似度计算的影响
传统的Pearson相似度计算,计算的时候所有商品都被赋予了相同的权重[15],并没有考虑到商品的热门程度对相似度计算的影响。如表2所示,大部分用户都对商品I1和I3给了评分,这两商品相对于其他商品更加流行[16]。

表2 用户-项目评分矩阵
从表2可知,用户U1和U2,U4和U5两组用户,共同评价商品数和具体评分值均相同,根据Pearson相似度计算公式,得出相同的相似度,即sim(U1,U2)=sim(U4,U5)。计算虽然正确,但不符合现实情况的逻辑。
从表2可看出项目1,3较项目2,4评分数目多,属于相对热门商品。例如一些人都买洗衣液,并不能很大程度上说明他们都喜欢此商品,洗衣液属于生活必需的热门商品,如果两用户都买了《推荐系统实践》,则能很大程度上说明他们都对此物品有更大的兴趣相似度。因此,对于热门程度不同的商品[17],在相似度的计算中,要赋以不同的权重。
本文引出热门商品惩罚因子,公式定义如下:

其中,n为商品的评分总数,ni为用户对商品i的评分值。物品越热门,n值越大,H(i)值就越小,该热门商品惩罚因子H(i)在惩罚热门商品的同时,对于冷门商品相似度计算的权值有了一定的提高,在降低热门商品对相似度计算影响的同时,也有利于对冷门商品的推荐[18]。
综合式(5)和式(6),把热门商品惩罚因子和平均评分修正因子融入相似度计算中,改进后的皮尔逊相似度为
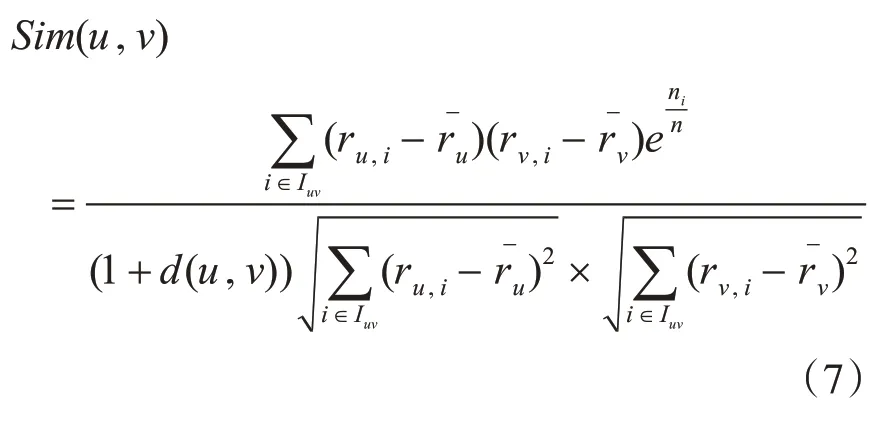
3.3 实验步骤
1)建立用户-项目评分矩阵,评分为5分制。
2)求取相似用户集N。利用式(7)计算目标用户和其他用户间的相似度,结果按大小顺序排列,前k个用户即为目标用户的相似用户集。
3)预测评分。根据相似用户集的历史评分数据预测目标用户对项目的评分,计算公式如下:

其中,N为目标用户u的邻居集,Sim(u,v)为改进后的皮尔逊相似度计算公式。
4)根据评分结果进行推荐。
4 实验结果及分析
4.1 实验数据集的介绍
本文实验数据集选取MovieLens数据集,该数据集是一个开源电影数据集,很多研究基于此数据集[19]。本文实验使用100kb的该数据集,包括1682部电影,943个用户和100,000条评论等数据,评分大小1~5分,此数据集包含以下几个属性:用户ID,电影ID,电影评分和评分时间,数据稀疏度[20]为93.7%。取80%评分作为训练集,剩余20%作为测试集,训练集用作用户相似度计算,后续对训练集中的未评分项目预测评分,测试集用于和某项目对应的预测评分作比较[21],以判断推荐准确率。
4.2 实验评定标准
本文采用平均绝对误差(MAE)来评估推荐质量。

N为测试集,实际评分为{rv,1,rv,2,rv,3,…rv,N},预测评分为{Rv,1,Rv,2,Rv,3,…Rv,N}预测评分和实际评分越接近,MAE就越小,推荐的准确率就越高。
4.3 实验结果和分析
本文选取传统的Pearson相似度算法,文献[11]提到的算法、文献[12]提出的相似算法和本文改进后的皮尔逊相似度计算方法进行实验,各算法计算流程均相同,不同算法的MAE值如图1所示。
由图1可知,除原始皮尔逊相似度计算公式外,其他算法的MAE值都有一定程度的降低,推荐准确度得到了一定的提高。文献[11]的算法通过引入共同评分项目占比,使相似度的计算更加准确,文献[12]的算法通过将用户共同评分项和用户所有评分项之间的关系引入相似度的计算更加有效地降低了MAE值。各算法均在相似用户数量50~60附近使MAE出现收敛,但本文提出的改进算法能更快地实现MAE值的收敛,且MAE值较其他方法更低,进一步提高了推荐的准确性。

图1 不同算法下的MAE值
5 结语
用户协同过滤是基于用户评分数据,计算用户间的相似度,通过相似邻居集来预测目标用户对未评分项目的喜好程度。本文通过分析传统相似度计算方法的缺陷,考虑到用户具体评分值和商品的热门程度对相似度计算的影响,提出了热门商品惩罚因子和平均评分修正因子,从而得到了一种优化的相似度计算方法。实验表明,改进后的相似度计算方法能在一定程度上提高推荐准确率。随着用户数据的进一步增加,数据的可扩展性将是推荐系统中亟待解决的问题,提高系统的可扩展性并为用户提供实时推荐,这些将是下一步的重要研究方向。
