毫米波在沙尘环境中损耗预测∗

2021-04-04周新力宋斌斌

计算机与数字工程 2021年3期

张涵周新力宋斌斌

（1.海军航空大学研究生管理大队烟台 264001）

（2.海军航空大学电子信息工程系烟台 264001）

1 引言

毫米波具有宽带宽、波束窄的特点，与激光相比，受气候传播的影响要小得多，具有全天候的特点。因此，毫米波随着无线电通信技术的不断发展，其在通信、制导、雷达、成像以及遥感技术和射电天文学等诸多领域中得到了普遍的应用，但毫米波传播波长短，容易在传播的过程中受到外界各种环境因素影响，传播衰减相对严重。在战场环境中传播，沙尘和烟雾的吸收和散射会造成信号的衰减，衰减的大小与沙尘的介电特性、粒子的形状、空间分布和谱分布等紧密相关。且战场环境中有大量的火焰燃烧造成的烟颗粒与空气混合，受到气流卷吸生成烟雾，加上炸弹爆炸成分中硫、磷、碳等粒子和某些有色气体及水汽的混合物［1］，它的烟雾成分是相当复杂的。

因为战场环境的复杂多变性，传播环境的衰减很难预测，其中沙尘和烟雾的相对介电常数还与水的含量相关，使得电波传播衰减更难预测［2］。对于电波在其中的衰减大多是依据实验数据进行测量，很少建立有系统的确定性模型。由于数据测量不仅需要复杂的测量设备，并且需要耗费大量时间、人力、物力以及大规模的试验场地，因此缺乏足够的实测数据。抛物方程（Parabolic Equation，PE）是一种高效的电波传播预测模型，能够直接反映电波传播的绕射和折射效应，无需修正传播机制的引入，最早由Leontovich和Fock在20世纪40年代提出，经过推广，目前已经成为水声传播和对流层电波传播等预测的主要模型。PE的数值解法主要有有限元分析法、时域有限差分方法以及分步傅里叶变换法（Split-step Fourier transform，SSFT）等。本文为提高在战场环境条件下电波特性预测的准确性，给出了一种基于PE的战场沙尘环境模型。该模型采用PE法实现准确快速求解，忽略掉相对复杂的粒子，只讨论毫米波在沙尘中的衰减，根据空气中沙尘不同含量求解出介电常数，通过抛物方程的方法，来预测战场沙尘环境衰减的抛物模型研究，最后经过仿真试验验证该模型有效。

2 抛物模型方程

假设电波于无源媒质间进行传播［4］，电磁场时谐因子是e-iwt，用标量u来表示任意一个与y方向无关电磁场分量，二维标量波动方程仅考虑前向传播，由此得到宽角抛物方程（Wide-Angle Parabolic Equation，WAPE）如下所示［5］：

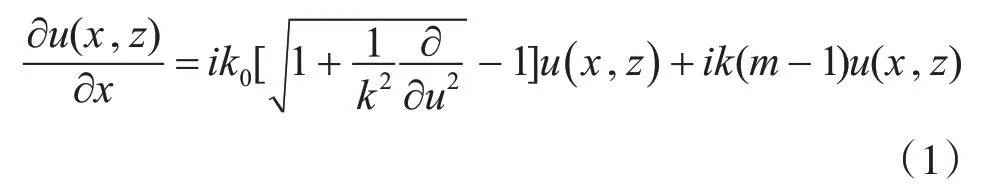
式（1）中m（x，z）=n（x，z）+z/ae为修正折射指数，由于地球曲率的影响引入z/ae，ae是地球的半径，为传播媒介的折射指数，ε为媒介介电常数、ε0为真空介电常数，μ为媒介磁导率、μ0为真空磁导率且μ和μ0都近似等于1，εr=ε/ε0是媒介的相对介电常数。WAPE的一种数值求解方法SSFT法，可以运用快速傅里叶变换结合步进方法，且其空间步长受波长限制极低，适用于求解在大尺度范围内的电波传播问题，SSFT解的形式［6］：

式（2）中指数ikΔx(m-1)反映的是不同媒介，对电波传播的影响，由此，为考虑电波传播的战场沙尘衰减特性，可使用战场沙尘媒介的等效介电常数，对PE模型的折射项进行修正得到。

3 沙尘的电磁建模

3.1 湿沙的复介电常数

由于战场沙尘所含粒子较为复杂，在本文中只研究其中含有沙粒和水分的情况。其复介电常数是频率和含水量的复合函数，通过两者之间的群粒子散射理论将其结合在一起，求得介电常数。

水的复介电常数可以通过双Debye公式求得：

式中ε0=77.6+103.3(θ-1) ；ε1=5.48 ；ε2=3.51 ；θ=300/T，其中T表示温度。

主弛豫频率和次弛豫频率分别为

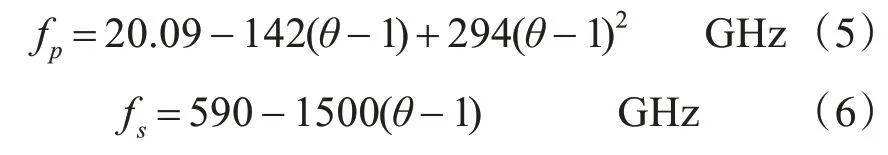
图1表示的是在0℃时和20℃时的曲线，频率变化是从1GHz～300GHz。对比曲线可以知道，水的复介电常数基本不随温度的变化而变化，但是随着频率的变化波动幅度较大。从图中可以看出，实部与虚部的变化有明显不同，随着频率的增大实部逐渐减小，在10GHz处明显减小，而随着频率的增大虚部先增大后减小，在20GHz～30GHz频率范围内，出现一个显著的峰值。

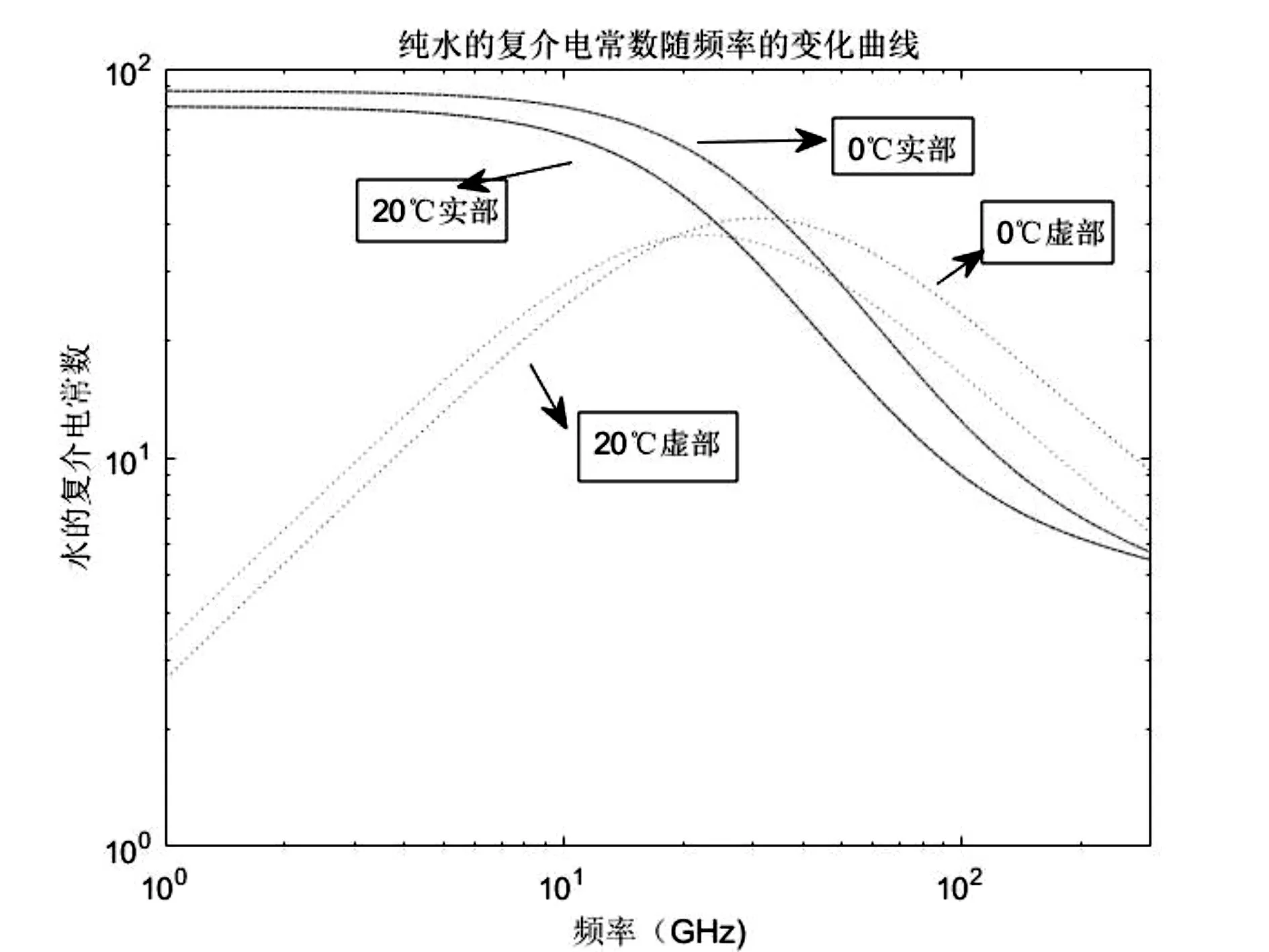
图1 纯水的复介电常数随频率的变化曲线

干沙的复介电常数的经验公式为［3］

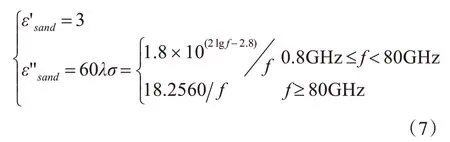
式中ε′和ε″分别为沙尘的复介电常数的实部和虚部，频率f以GHz为单位。

可以假设沙尘中的干沙粒子是近似为球形。求解沙尘中湿沙粒子的等效介电常数εe，可以通过推导麦克斯韦方程来得到：

上式中，εw代表水的复介电常数，εsand代表干沙的复介电常数，p代表水的体积百分数。

图2、图3显示了干沙和水在20℃不同混合比例时频率增加引起的变化趋势，含水量分别为0%、10%、15%、20%，由图2可见，随着频率的增加，湿沙的复介电常数实部逐渐减小，但是其变化的波动不大，图3可知湿沙的复介电常数虚部随频率增加而迅速增大，并且含水百分比越大，数值越大。

图2 湿沙不同含水量复介电常数实部

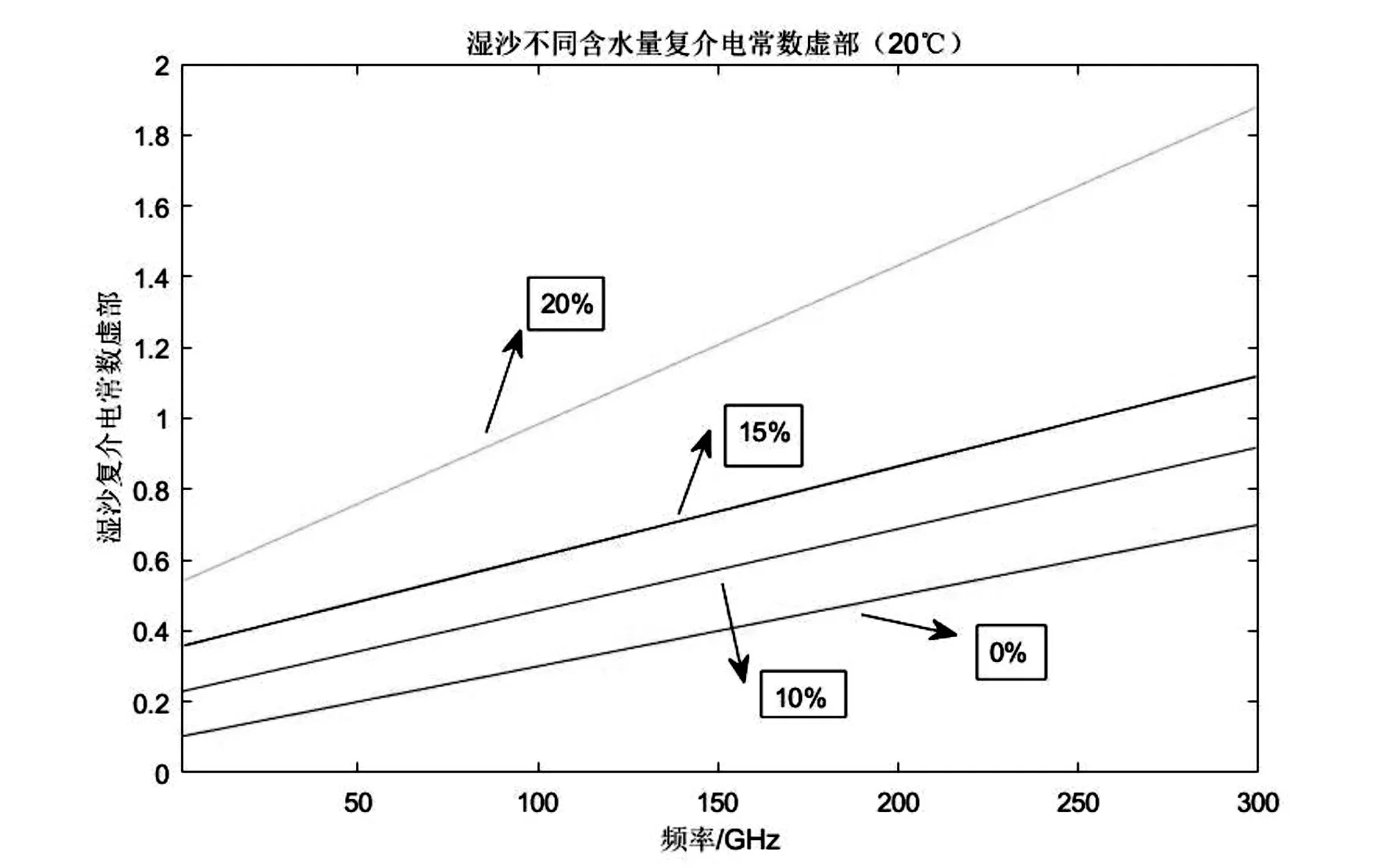
图3 湿沙不同含水量复介电常数虚部

3.2 沙尘的相对介电常数

本文将稀疏分布的悬浮粒子组成的沙尘看做一种等效介质，其尺寸分布在几十μm到几百μm范围内，由文献［7］可知，直径为D的沙尘粒子在单位体积内的个数N（D）可表示为

式中N0为沙尘的体密度（1/m3）；p（D）为尺寸分布密度：

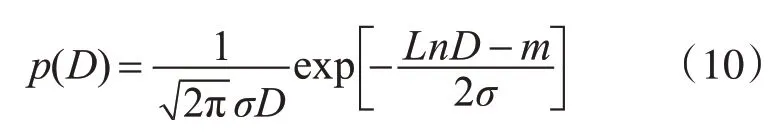
式中，m和σ为参数LnD的均值和标准偏差。文献［8］给出了中国腾格里沙漠和黄河沙滩沙尘样品的沙尘参数（LnD）的均值m，标准偏差σ，体密度N0如表1所示。

表1 不同地区沙尘参数

实际中体密度N0很难测得，为获得相对准确的数据，国内外学者通常利用光学能见度来计算其值，两者关系为［9］

沙尘实际为沙尘粒子弥散在空气中，并按照一定的普分布规律，形成了一种宏观上接近均匀的随机介质。假定沙尘的等效介电常数为εeff，则沙尘区中的电位移矢量为

如上文所说，假设沙尘粒子为球形粒子，则根据文献［10］：

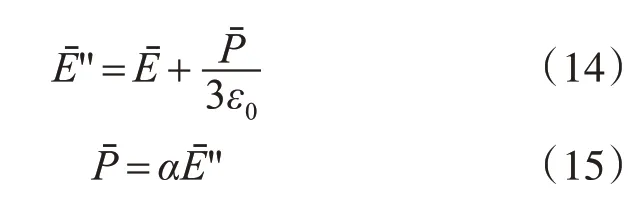
由上式可推导出：

沙尘粒子的极化率为［11～15］

其中，εe为沙尘气溶胶中粒子所属物质的介电常数。由上式可得沙尘的等效介电常数为

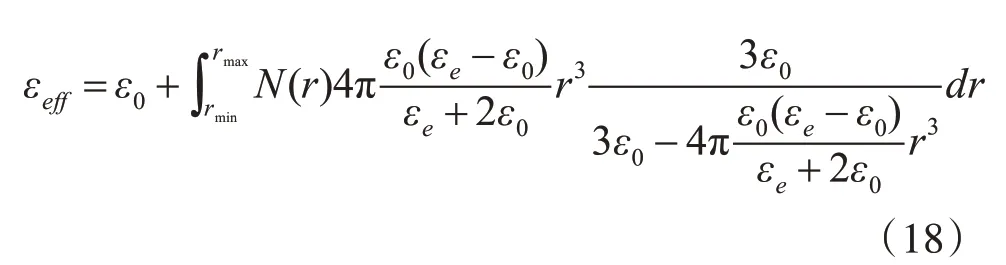
由公式可知，根据沙尘粒子的能见度可以计算出沙尘粒子的体密度分布，带入上式可以计算出沙尘的等效介电常数。

4 仿真分析

将构建的基于PE的战场环境模型应用于给定环境的电波传播特性预测中进行仿真验证。假设发射天线高15m，毫米波系统的工作频率为35GHz，高斯方向图，水平极化，接收天线高12m，标准大气，取战场沙尘的粒子浓度为30g/m3，粒子半径为0.02mm，介电常数为3-j1，将抛物模型情况与文献［4］的模型进行对比。

图4 抛物方程计算烟尘衰减验证

图4显示了毫米波在战场沙尘环境中传播产生的损耗值，采用沙尘等效介电常数与经验模型进行比较。可以看出，采用本文模型对毫米波在沙尘环境中传播损耗预测，小于采用经验模型预测的计算结果，且结果较为接近。这主要是由于PE模型的数值解具有相对良好的稳定性和准确性，更重要的是可以同时考虑大气折射对电波传播的影响。由此可见，相对于经验模型而言，采用在抛物模型的基础上对沙尘环境预测的形式更能准确地反映战场沙尘环境对电波传播的影响。