不通过自由纸面时建立时间基准的方法与性能分析
2021-04-01伍贻威王世超
伍贻威,王世超
北京卫星导航中心,北京 100094
协调世界时(coordinated universal time,UTC)是一个国际上的时间基准,由国际计量局(Bureau International des Poids et Mesures(in French),BIPM)计算并每月发布一次[1-2]。守时实验室和全球导航卫星系统(GNSS)都需要建立时间基准。守时实验室的时间基准记为UTC(k),其中k为实验室代号。例如,中国国家授时中心(NTSC)建立和保持UTC(NTSC);美国海军天文台(USNO)建立和保持UTC(USNO)。按照国际电信联盟(The International Telecommunication Union,ITU)的要求,[UTC-UTC(k)]的偏差要求保持在100 ns以内[1]。GNSS的时间基准记为GNSST(GNSS time)。例如,美国GPS的时间基准记为GPST(GPS time);中国北斗卫星导航系统(BeiDou system,BDS)的时间基准记为BDT(BeiDou time)。GNSST一般溯源至某个UTC(k),[UTC(k)-GNSST]一般保持在几十纳秒甚至更小的量级(本文中不加说明都是指mod 1 s的偏差)[1]。GNSST的性能将直接影响GNSS导航、定位、授时的性能。
传统建立GNSST的方法分两步:第1步,综合钟组内所有的原子钟,建立一个自由纸面时;第2步,将该自由纸面时溯源至某个UTC(k),即使用该UTC(k)驾驭该自由纸面时,得到GNSST[2-5]。以建立GPST为例[5],第1步,综合GPS地面和卫星上的原子钟,采用某种时间尺度算法(Kalman滤波器算法),建立了一个自由纸面时;第2步,采用UTC(USNO)驾驭该自由纸面时,得到GPST,确保[UTC(USNO)-GPST]保持在一定范围内。建立BDT也采用了类似的两个步骤。目前的BDT为纸面时间,它是BDS导航、定位、授时的时间基准;如果是要指明其物理信号,一般的文档中都会强调“BDT的物理信号”。BDT的物理信号是某一台原子钟使用相位微跃计经过(时间、频率等)调整后的信号,即再进行1次驾驭,采用BDT驾驭某一台钟,产生BDT的物理信号,确保BDT的物理信号和BDT保持在一定范围内。
目前,国内外对于建立时间基准的研究,大部分还局限在传统方法的基本框架下,期望通过优化设计时间尺度算法和驾驭算法来提升时间基准的性能(具体算法优化设计参见文献[4—19]),并没有对传统方法本身进行改进。传统方法的固有属性造成方法本身存在不足,主要原因在于单台钟的时差和自由纸面时是相互影响的,以及由此导致的其他不足,这并不是通过优化设计算法就可以得到改善的。
针对这种情况,本文摈弃了传统方法的基本框架,从方法本身进行优化,提出一种方法,即不通过自由纸面时建立时间基准的方法。本文方法的核心思想是对每台钟分别设计预测算法和驾驭算法,这样每台钟都可以独立得到一台受驾驭钟,然后再对这些受驾驭钟进行加权平均。该方法避免了传统方法自身的不足,此外还可以针对每台钟的特性分别优化设计预测算法和驾驭算法。
1 传统方法的基本原理
传统方法建立GNSST包括两个步骤,分别对应着1.1节和1.2节所描述的两个核心算法:时间尺度算法和驾驭算法。其中时间尺度算法中又包含了预测算法和权重算法。后续产生GNSST的物理信号时,还需要在此基础上再进行1次驾驭[4-5],本文中不展开描述。
1.1 建立自由纸面时的时间尺度算法
时间尺度算法的目的是综合钟组内的原子钟,建立一个更稳定更可靠的自由纸面时,其形式上包括加权平均算法和一系列的Kalman滤波器算法。任何加权平均形式的时间尺度都可以化简,最终由时间尺度基本方程(basic time scale equations,BTSE)来表达[3-7]。实际上,采用Kalman滤波器形式建立的时间尺度都可以化简并以BTSE来表示。因此,一系列的Kalman滤波器算法,本质上也是加权平均算法。
自由纸面时(temps atomique (in French),TA)通过BTSE表示为[3-7]
(1)
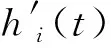
时间尺度算法中的核心算法为权重算法和预测算法,分别用于确定权重和预测值。
预测算法可以参考ALGOS的预测算法选取:①类似于2011年前的ALGOS原始预测算法,采用一次多项式模型[7];②类似于2011年后的ALGOS新预测算法,采用二次多项式模型预测[10-11]。
权重算法也可以参考ALGOS的权重算法选取:①类似于2014年前的ALGOS原始权重算法[7],反比于频差方差或Allan方差;②类似于2014年后的ALGOS新权重算法[8],反比于预测误差的平方。

xi(t)=TA(t)-hi(t)
(2)

图1为时间尺度算法的基本原理。第1台钟为参考,x1i=x1-xi代表第1台与第i台钟的共N-1组时差(无观测噪声),通过时间尺度算法,迭代计算出N台钟的时差xi=TA-hi。
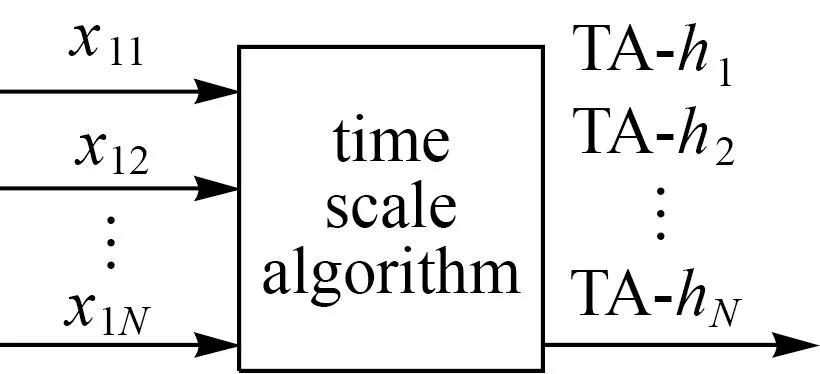
图1 时间尺度算法的基本原理Fig.1 Basic principle of time scale algorithms
1.2 驾驭自由纸面时产生时间基准的驾驭算法
驾驭,本质上是负反馈控制。设计驾驭算法,需要综合运用自动控制的相关理论[12-13]。有多种形式的驾驭算法可供灵活选取,包括UTC(USNO)驾驭产生GPST的线性高斯二次型(linear Gaussian quadratic,LGQ)算法[14]、数字锁相环(digital phase-locked loop,DPLL)算法[15-16]等。
图2描述了采用DPLL算法,用UTC(k)驾驭GNSS的TA,产生时间基准(GNSST)的基本原理。根据[UTC(k)-GNSST]和DPLL的开环传递函数(Z域中以G(z)表示),计算出对于TA的时间、频率和频漂的调整量,调整TA,产生GNSST[15-16]。
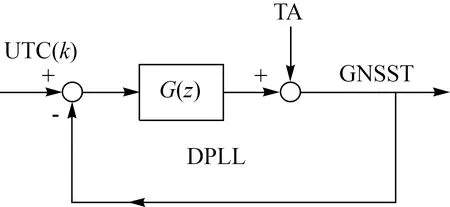
图2 驾驭的基本原理Fig.2 Basic principle of steering
其原理类似于GNSS接收机通过解算得到GNSST相对于内部晶振的时差,计算出对晶振的时间、频率和频漂的调整量,调整晶振,输出代表GNSST的时间信号[17]。
驾驭算法的核心是设计合理的传递函数。传递函数决定了驾驭性能[15-16]。图2中的DPLL是数学上的DPLL,不是物理上的DPLL,它的作用是计算出每次的控制量(调整量),在数学上(纸面上)对GNSST进行调整。这样每次获得[UTC(k)-GNSST]后,DPLL就可以通过传递函数G(z)自动计算出调整量,通过负反馈控制自动生成GNSST。
本文把对TA的累计时差调整量记为Δ,即TA+Δ=GNSST。
综上,结合式(1),在t时刻的[UTC(k)-GNSST]表示为
[UTC(k)-GNSST](t)=UTC(k)(t)-
(3)
2 不通过自由纸面时建立时间基准的方法
2.1 传统方法的不足与本文方法的基本思路
传统方法在迭代计算TA的过程中,每台钟的权重和预测值都是根据式(2)的时差,即TA-hi计算得到的,所以单台钟的时差和TA是相互影响的。这就导致以下问题。
(1) 在某些情况下,例如当钟组规模较小时,并不能保证TA的频率稳定度远高于单台钟,即Allan方差小1个数量级或Allan偏差低至1/3。这时,根据TA-hi计算得到的权重,其中叠加了TA的影响,并不完全反映单台钟的频率稳定度性能或预测性能。如果TA的频率稳定度还没有单台钟高,这时时差TA-hi反映的是TA的而不是单台钟的频率稳定度。同理,根据TA-hi计算得到的预测值,其预测不确定度也大于单台钟相对于理想时间尺度的预测不确定度。
(2) 正是由于预测值都是根据TA-hi计算得到的,所以预测值的实际作用是扣除单台钟相对于TA的(时间、频率等)偏差,而不是其相对于理想时间尺度的偏差。这就导致,预测值的初值对TA的影响巨大。一旦预测值初值相对于外参考UTC(k)出现较大的偏差,TA就会相对于参考UTC(k)出现较大的偏差。
同理,当某一台钟出现频率跳变等异常而没有检测出来,将直接导致TA的频率跳变。例如:假设某一台铯钟发生1×10-13的频率跳变没有被检测出来,其权重为10%,那么将引起TA大约1×10-14的频率改变。
由于后续的预测值同样是根据TA-hi计算得到的,后续时间段内TA改变的频差会一直被保留下来(尽管TA不考虑频率准确度的问题),这个过程是不可逆的。
(3) 时间尺度算法中对于每台钟的预测值的预测间隔都一致,实际上这并不是一种最优的方法。按照文献[18—19],对于不同类型的原子钟,如果根据它们的不同噪声特性,分别确定频差的最优观测间隔,可以分别优化预测效果。
(4) 对于分布式守时或星地联合守时,由于部分星载钟不可视、比对链路中断、部分原子钟故障等原因,导致参与TA计算的原子钟数量改变,进而导致TA噪声性能的改变。如图2所示,由于驾驭算法的结构、带宽、参数等需要根据TA的性能来优化设计,这时根据实际情况来重新设计或者自适应调整驾驭算法并不容易。
针对传统方法的不足,本文提出一种不通过自由纸面时建立时间基准的方法。本文方法的核心是对每台钟分别优化设计预测算法和驾驭算法,这样每台钟都可以独立得到一台受驾驭钟,然后再对这些受驾驭钟进行加权平均。通过该方法,避免了计算权重和预测值时由于单台钟和TA相互影响导致的算法固有不足,还可以针对每台钟的特性分别优化设计预测算法和驾驭算法。图3为本文方法的原理。
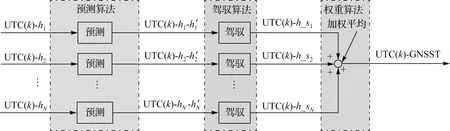
图3 本文方法的基本原理Fig.3 Basic principle of the new method
方法具体步骤如下。
(1) 综合[UTC(k)-GNSST]和[GNSST-hi],换算得到时差[UTC(k)-hi],记为xi。后续所有权重和预测值都是由时差xi计算得到。
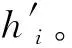
(4) 权重可以根据实际需求来灵活选取。考虑到GNSS对自主导航时的时间自主保持能力要求较高,本文中的权重算法采用类似于BIPM在2014年后的ALGOS新权重算法,以优化时间同步精度为目的。对所有h_si加权平均后得到GNSST。为了避免由于钟组中钟数量、各台钟的权重等发生变化而引起GNSST在时间上的不连续,和步骤(2)类似,同样需要在相邻间隔点处引入时间修正量。
根据上述描述,在t时刻的[UTC(k)-GNSST]表示为
[UTC(k)-GNSST](t)=
(4)
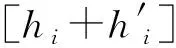
2.2 理论分析
(1) 本文方法和传统方法的核心算法都是预测算法、驾驭算法和权重算法,但是顺序不同。传统方法中,预测算法和权重算法是并行运行的,都包含在时间尺度算法中;时间尺度算法通过多次迭代计算后,同时得到权重、预测值、时差xi=TA-hi;然后再使用驾驭算法,用UTC(k)驾驭TA得到GNSST。由图3可知,本文方法中,预测算法、驾驭算法和权重算法是依次顺序进行的,预测值、驾驭量和权重都是依次计算得到的。
(2) 根据上文由传统方法和本文方法得到的[UTC(k)-GNSST]分别表示为
[UTC(k)-GNSST](t)=UTC(k)(t)-
[UTC(k)-GNSST](t)=UTC(k)(t)-
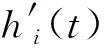


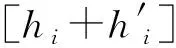
(5) 假如在图3中,本文方法的驾驭算法和权重算法更换前后顺序,即按照预测算法、权重算法、驾驭算法的顺序建立时间基准,依然是可行的。这时本文方法和传统方法在形式上比较接近;即前两个步骤,通过预测算法和权重算法,建立一个非自由的时间尺度,然后再使用驾驭算法,通过UTC(k)驾驭该非自由的时间尺度得到GNSST。这时本文方法依然可以避免传统方法的前两个不足。但是,这时本文方法不能像图3那样,充分发挥针对每台钟分别优化设计驾驭算法的优势。这也就是本节两个表达式最后1项的区别。
2.3 不同原子钟性能
原子钟时差(UTC(k)-hi)表示为[21-23]
xi(t)=xi,0+yi,0t+1/2·dit2+σi,1Wi,1(t)+
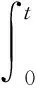
(5)
式中,i代表第i台钟;xi,0、yi,0和di分别代表时差、频差和频漂的初值;Wi,1(t)和Wi,2(t)分别代表两个独立的维纳过程,它们都服从N(0,t),σi,1和σi,2分别是这两个维纳过程的扩散系数。
后两项为噪声项,分别代表了频率白噪声(WFM)和频率随机游走噪声(RWFM)。原子钟噪声是有色噪声[24],一般通过Allan方差[22-23]来表征其频率稳定度
(6)
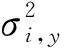
通过实测钟差、BIPM和国际GNSS监测评估系统(International GNSS Monitoring & Assessment System,iGMAS)的服务器公开下载的地面钟或星载钟钟差,分析各原子钟的性能。表1列出了俄罗斯VCH-1003M氢钟、美国MHM2010氢钟、国产SOHM-4氢钟、铯钟、星载氢钟、星载铷钟的平方扩散系数和频漂幅度的估计值。图4画出了这些原子钟(氢钟和铷钟已扣除频漂)的Allan偏差(Allan方差的平方根)曲线。由文献[25—26]可知,不同GNSS星载钟的性能差异较大,包括BDS-2、BDS-3各星载钟的性能差异也较大。表1中,地面钟为典型值,星载钟为其中某1台的估计值。

表1 不同原子钟的参数
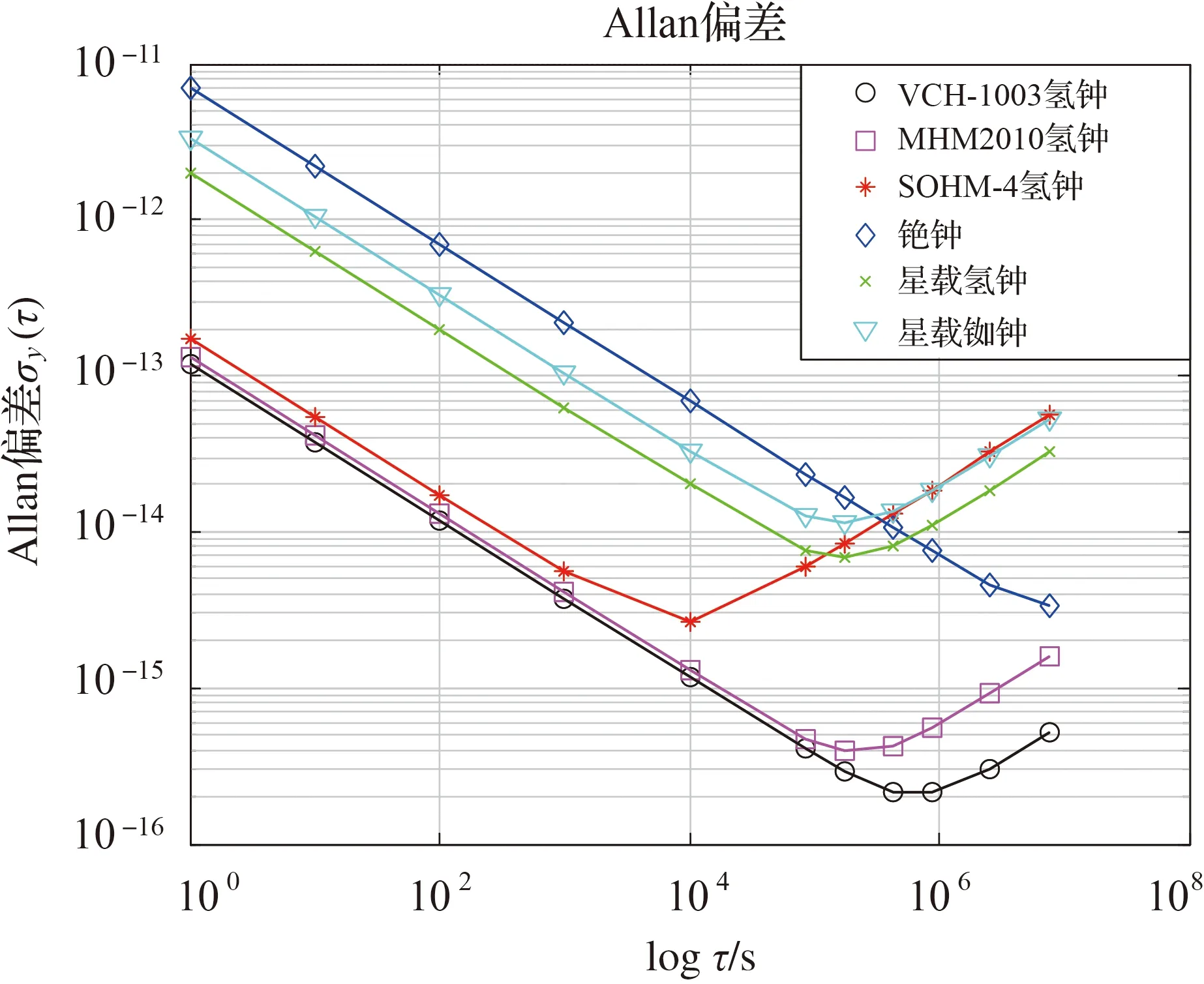
图4 不同原子钟的Allan偏差曲线Fig.4 Allan deviation curves of different clocks
噪声方差表示为[22-23]
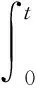
(7)
图5为按照表1的参数和文献[27]的方法仿真生成的100台铯钟的时差(确定性部分为零,只含噪声,图中绿色曲线),以及由式(7)的1倍和2倍平方根计算得到的1σ和2σ噪声标准差(黑色加粗曲线)。图5展示了作为有色噪声的WFM和RWFM的标准差随时间的变大而变大。式(7)和图5说明:原子钟的长期稳定度(去除频漂后)越好,其时间长期自主保持能力就越好。对于表1所列原子钟,显然VCH-1003M氢钟的时间长期自主保持能力最优。
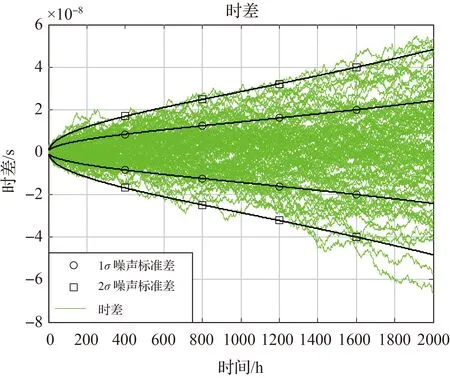
图5 100台仿真铯钟的时差、1σ和2σ噪声标准差的理论值Fig.5 Time differences of 100 cesium clocks, 1σ and 2σ theoretical noise standard deviations
2.4 预测算法
假如采用一次多项式模型预测,预测误差通过[真实值-预测值]表示为
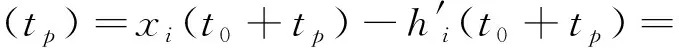
(xi,0+yi,0·tp+σi,1Wi,1(t0+tp)+
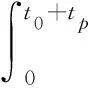
(8)
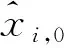
假如预测模型符合原子钟模型,预测是无偏的,预测误差服从以下分布
(9)
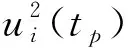
当观测间隔Ti,1较长时,测量噪声的影响可以近似忽略。这时有[18-19]
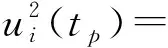
(10)
式中,Ti,1为频差的观测间隔。
表2列出了根据表1的参数计算得到的各原子钟的频差最优观测间隔。
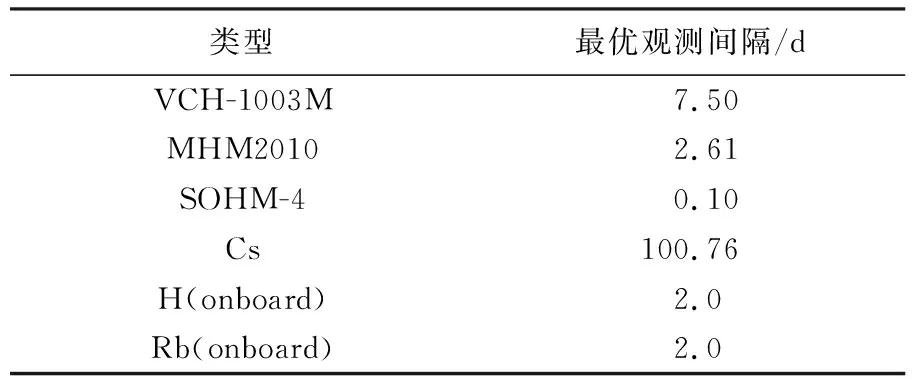
表2 不同原子钟的频差最优观测间隔
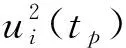
根据表1和表2,不同原子钟的噪声特性不同,最优观测间隔也相差很大。本文方法中针对不同原子钟分别优化选取观测间隔,目标是提升预测性能。
对于存在明显频漂的原子钟,需要采用二次多项式模型,才能保证预测是无偏的。文献[19]推导证明
(11)
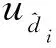
式(11)表明:T2越大,频漂的估计不确定度越小。BIPM的ALGOS新预测算法中,对于T2曾经尝试过取3个月、4个月和6个月等[11]。

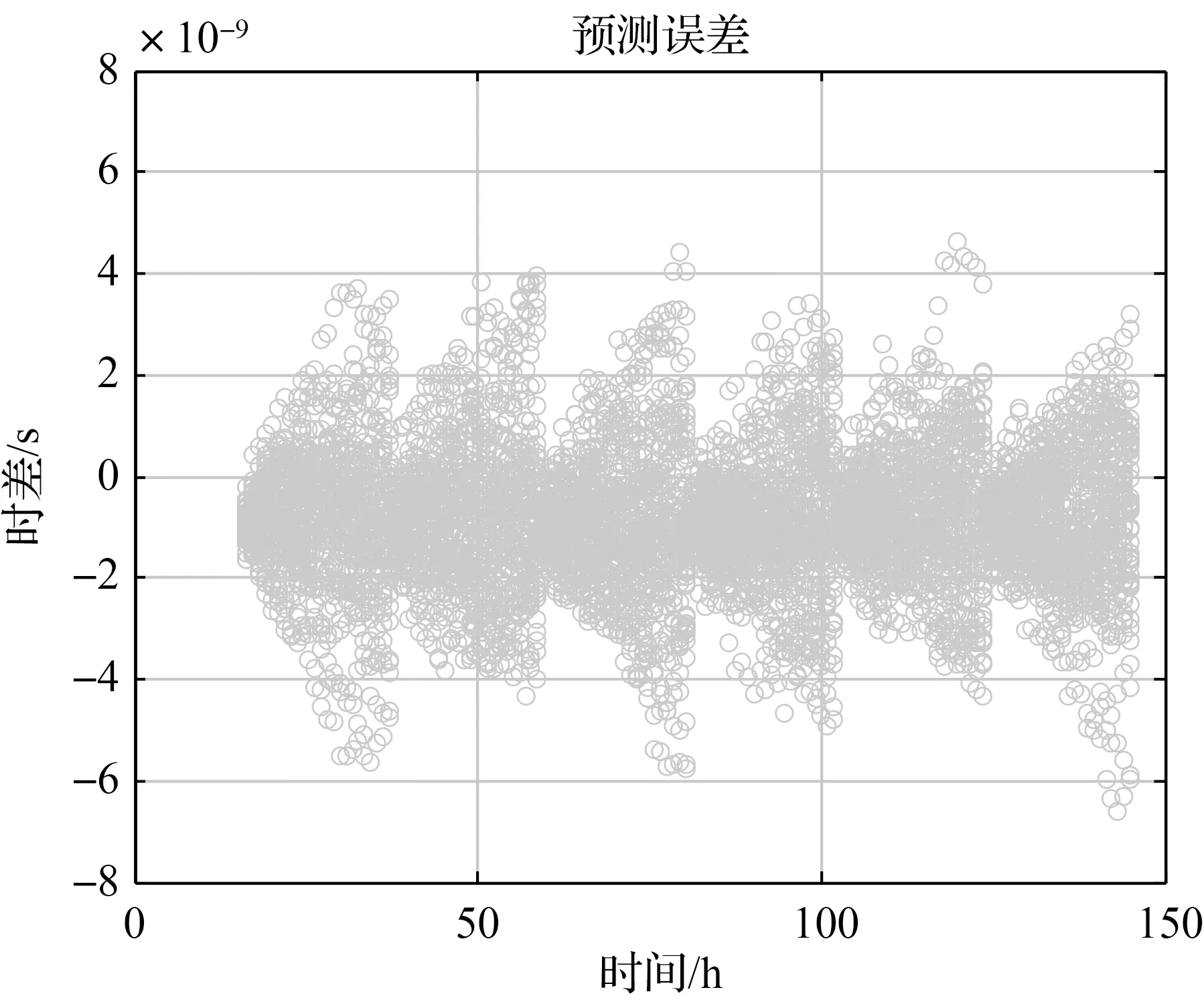
图6 50台铯钟的预测误差曲线Fig.6 Prediction error curves of 50 cesium clocks
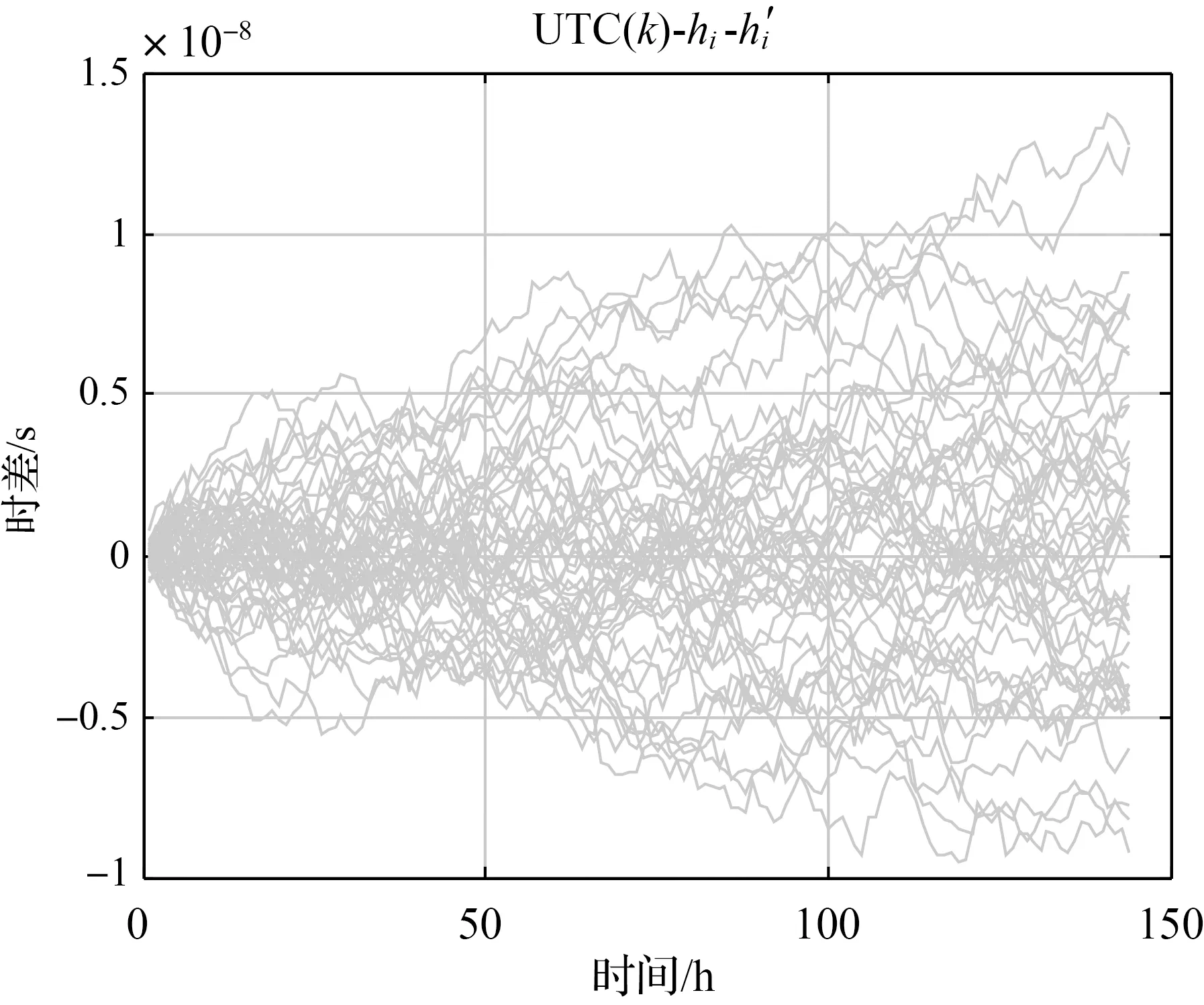
图7 50台仿真铯钟的曲线
图6和图7的曲线都扣除了预测值且和UTC(k)保持时间和频率同步,但主要受原子钟噪声的影响(参考图5),它们与UTC(k)的偏差随着时间变大而变大。
2.5 驾驭算法
驾驭算法的目的是通过负反馈控制,将负反馈的输出信号GNSST和输入信号UTC(k)的时间、频率、频漂尽量调整到一致。本文采用文献[16]描述的等价于Kalman滤波器加延迟器的三阶3类DPLL算法。这时,图2中的开环传递函数为

(Ksi,2+(1/2)Ksi,3T)
(12)
式中,T为每次驾驭的时间间隔;(Ksi,1,Ksi,2,Ksi,3)为DPLL的增益。在该算法中,DPLL的增益等价于稳态Kalman增益,参数(Ksi,1,Ksi,2,Ksi,3)的值由Kalman滤波器的R值决定。文献[16]详细描述了针对不同噪声特性的原子钟,合理选取参数的方法。
2.6 权重选取
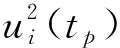
对M个时差预测误差的平方进行滤波,参考ALGOS新权重算法[8],滤波结果设置为(k≥M时)
(13)
式中,i、k表示第i台钟第k个间隔。
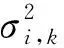
最终,第i台钟第k个间隔的权重为
(14)
该权重算法直接优化了[UTC(k)-GNSST]的时间同步精度。由于预测不确定度和Allan方差之间存在函数关系,因此算法也间接优化了GNSST的频率稳定度。
3 试验分析
3.1 传统方法TA性能分析实测数据试验
本试验展示某台铯钟频率异常对于TA的影响。采用5台钟的实测数据,包括3台VCH-1003M氢钟、两台铯钟,把1台和UTC保持同步的VCH-1003M氢钟当作外参考UTC(k),而另外4台钟组成钟组用于建立TA。图9画出了[UTC(k)-hi]的一次多项式残差,其中H1和H2分别为2台VCH-1003M氢钟,Cs1和Cs2为两台铯钟。数据长度共35 d,时差采样间隔为60 s。
积累20 d数据。从第21 d 0点开始,采用上文描述的传统方法中的时间尺度算法,选取每个间隔为6 h,即每隔6 h计算一次TA。TA长度共14 d,共56个间隔。在进行TA计算之前,先按照文献[28]的Kalman滤波器方法滤除[UTC(k)-hi]的测量噪声。权重按照式(13)和式(14)选取,M=12。限制每台钟的最大权重为1.6/N(N=4为钟组内钟的数量),这样两台氢钟最高只能获得80%的总权重。所有预测值采用二次多项式模型计算,且频差预测值的观测间隔等于GNSST的计算间隔,即6 h。
共进行两次试验。第1次为不存在异常的情况。第2次试验时人为在第25天0点(TA的第5天0点)给Cs2加入1.5×10-13的频率跳变。
图10(a)为两次试验的[UTC(k)-TA]时差曲线。由[UTC(k)-TA]的时差差分可以得到的每个间隔的频差。图10(b)为两次试验的[UTC(k)-TA]的频差之差。图11为两次试验中Cs2的权重变化。实际上两台氢钟一直都取满权,共获得80%的总权重;两台铯钟分配了剩下的20%的权重。因此,用20%减去Cs2的权重即可得到Cs1的权重。
由图11可知,在TA的第5天0点(第17间隔的起始时刻)发生频率跳变后,根据式(13)和式(14),由于Cs2的预测误差变大,Cs2的权重立即由第16间隔的15.45%下降至第17间隔的9.51%。尽管如此,该跳变还是对TA频率产生了较大影响。按照“Cs2跳变幅度×Cs2权重”估算TA频率改变的幅度,近似为1.5×10-13×9.51%=1.43×10-14。由图10(b)可知,Cs2发生跳变后,后续时间段TA相比无频率跳变时TA的频率改变在1.4~1.6×10-14。由图10(a)可知,TA频率改变后在时差上的积累效果。
综上,本次试验展示了传统算法的不足。单台钟的频率改变会造成TA的频率改变;由于预测值是根据xi=TA-hi计算得到的,后续所有时间段,TA以及其他钟时差xi=TA-hi的频率都发生了改变,该频率改变会一直被保留下来,这个过程是不可逆的。除此之外,假如本次试验中,某1台氢钟因故障下线,钟组中少了1台氢钟,两台铯钟的权重会显著上升,将造成TA的频率稳定度特性的明显改变,可以预见这对于后续驾驭算法的设计是很不利的。
3.2 本文方法与传统方法对比分析仿真数据试验
采用仿真数据,对比分析本文方法和传统方法建立的GNSST的性能。按照表1的参数,仿真生成1台和UTC保持同步的VCH-1003M氢钟作为外参考UTC(k);仿真生成两台VCH-1003M氢钟、两台MHM2010氢钟、两台SOHM-4氢钟、两台铯钟、两台星载氢钟、两台星载铷钟共计12台钟组成钟组,用于建立GNSST。设置观测噪声为零。所有钟采用二次多项式模型进行预测。限制单台钟最高权重为1.6/N。取M=12。每个间隔tp=1 d,即每隔1 d预测和驾驭1次,共1080个间隔(3 a)。共进行3次试验,分别建立时间基准(GNSST)。
第1次采用传统方法。所有预测值采用二次多项式模型计算,且频差预测值的观测间隔选取为GNSST的计算间隔(1 d)。驾驭算法的DPLL增益参数值选取为(Ksi,1,Ksi,2,Ksi,3)=(0.504,2.025 4×10-6,4.066 1×10-12)。权重按照式(13)和式(14)选取。
第2次采用本文方法。预测算法、驾驭算法、权重算法和第1次试验完全相同,即频差预测值的观测间隔选取为1 d,所有钟的DPLL的增益参数值都选取为(Ksi,1,Ksi,2,Ksi,3)=(0.504,2.025 4×10-6,4.066 1×10-12)。权重算法不变。
第3次采用本文方法,并采用优化的预测算法。参照表2,它们的频差观测间隔分别选为7.5 d、2.5 d、0.1 d、20 d(对于铯钟预测时间为1 d的情况,20 d已经足够长)、2 d和2 d。所有钟的驾驭算法和参数、权重算法都不变。
图12(a)为3次[UTC(k)-GNSST]的时差,图12(b)为3次GNSST的Allan偏差。分析试验结果如下:
(1) 在传统方法中,4台进口氢钟一直取满权;两台国产氢钟大约半数的间隔取满权;铯钟和星载铷钟的权重相对较小。在本文方法中,4台进口氢钟一直取满权;两台国产氢钟几乎一直取满权。可见本文方法有效发挥了国产氢钟tp=1 d时的预测性能的优势。
(2) 图12(a)表明,在采用相同的预测算法、驾驭算法、权重算法以及相同的参数时,本文方法(第2次试验,红色曲线)的[UTC(k)-GNSST]的时间同步精度为0.136 ns,最大偏差的绝对值<0.6 ns,明显优于传统方法(时间同步精度为0.730 ns,最大偏差的绝对值<2.1 ns);当本文方法优化频差预测值的观测间隔后(第3次试验,绿色曲线),[UTC(k)-GNSST]的时间同步精度为0.133 ns,最大偏差的绝对值<0.5 ns,相比第2次试验有优化,但效果不显著。
(3) 假如参考时间尺度的频率准确度比被评价时间尺度的频率准确度高1个数量级,频率准确度可以采用它们的相对频率偏差的绝对值的最大值来描述。从直观上理解,[UTC(k)-GNSST]的时间同步精度越高,说明GNSST与UTC(k)越接近,相对频率偏差越小。本次仿真试验中,采用长度为7 d的滑动窗,计算1080 d中,[理想时间尺度-UTC(k)]、第1次试验、第2次试验、第3次试验[UTC(k)-GNSST]的相对频率偏差的绝对值的最大值,分别为1.28×10-15、4.04×10-16、1.20×10-16、1.08×10-16。这说明,[理想时间尺度-UTC(k)]的频率准确度在10-15量级,[UTC(k)-GNSST]的相对频率偏差保持在10-16量级,所以GNSST的频率准确度和UTC(k)在一个数量级(10-15),相比于UTC(k)仅略有恶化。
(4) 图12(b)表明,本文方法建立的GNSST的Allan偏差在平滑时间>2×105s时优于传统方法,在平滑时间<2×105s时略差于传统方法(例如平滑时间=2×104s时,传统方法约为1.5×10-15,本文方法约为2.0×10-15)。后续需要在本文的基础上,进一步分别针对每台原子钟优化设计驾驭算法,提升GNSST的频率稳定度。
综上,仿真试验的结果与理论预期相符。在相同的算法和参数情况下,本文方法的[UTC(k)-GNSST]时间同步精度明显优于传统方法;优化预测算法后,提升了时间同步精度,但效果不显著;采用本文方法时,GNSST的频率稳定度在平滑时间>2×105s时优于传统方法。
3.3 试验结果分析与讨论
3.3.1 时间同步精度
在采用完全相同的预测算法、驾驭算法、权重算法及相同参数的情况下,本文方法建立的GNSST(图12红色曲线)的[UTC(k)-GNSST]时间同步精度明显优于传统方法(图12黑色曲线),主要原因在于:外参考UTC(k)为1台与UTC同步的VCH-1003M氢钟,由图4可知其频率稳定度比其他钟更高。传统方法中,由于限制了每台钟的最大权重,两台VCH-1003M氢钟只占了约30%的权重,因此外参考UTC(k)的频率稳定度比TA也更高。所以,本文方法中预测算法根据xi=UTC(k)-hi的预测不确定度比根据xi=TA-hi的结果更小。
由此推测出:本文方法应用于建立BDS星间时间基准,预期可以获取较优的时间同步精度。主要原因为,UTC(k)的频率稳定度优于BDS星载钟以及由BDS星载钟建立的TA,本文方法中预测算法根据xi=UTC(k)-hi的预测不确定度将明显优于传统方法根据xi=TA-hi的结果。
3.3.2 频率准确度
从频率准确度的定义可知,随着[UTC-UTC(k)]和[UTC(k)-GNSST]时间同步精度的提高,GNSST的频率准确度也将得到提高。本次仿真试验仿真生成了单台钟,获取单台钟与理想时间尺度的偏差。但这在实际上是无法实现的。实际上能够得到的仅是两个时间尺度之间的偏差。GNSST频率准确度可以根据[UTC-UTC(k)]和[UTC(k)-GNSST]换算得到的[UTC-GNSST],先计算其相对频率偏差,再结合UTC的频率准确度来综合评价。BIPM建立UTC时采用了数十台秒长基准(喷泉钟)驾驭国际自由原子时(EAL),因此UTC的频率准确度(相对于理想时间尺度)是这些秒长基准的自评定的频率不确定度的加权平均值,目前为10-16量级。本次仿真试验表明,[UTC(k)-GNSST]的相对频率偏差可以做到10-16量级。假如[UTC-UTC(k)]的相对频率偏差保持10-15量级,最终可以确保GNSST的频率准确度在10-15量级。
3.3.3 频率稳定度
由上可知,权重直接优化了预测性能,同时间接优化了频率稳定度。在本文方法中,长期频率稳定度更优的钟预测性能更好,相比传统方法获得了更高的权重。所以,本文方法的长期频率稳定度更优。
图12(b)的3条Allan偏差曲线在平滑时间1×105s左右有凸起现象,与驾驭算法的设计有关。当DPLL的带宽设计得较窄时,时间同步精度会提高,但中短期频率稳定度会有一定的恶化[18-19]。因此,未来需要针对每台钟的特性,综合考虑时间同步精度和频率稳定度的性能,进一步优化设计驾驭算法。
4 结束语
本文提出了一种不通过自由纸面时建立时间基准的方法。完整展示了该方法的核心思想、步骤,理论优势,以及预测算法、驾驭算法和权重算法的设计原理。试验结果初步验证了本方法的优异性能。本方法避免了自由纸面时计算过程中因单台钟和TA相互影响而造成的不足,还可以针对每台钟分别优化设计预测算法和驾驭算法,相比传统方法具有优势。
本方法不仅可以用于建立GNSST,还可以用于建立UTC(k)。以中国国家授时中心(NTSC)为例。传统方法[29-30]为:采用类似于ALGOS算法的时间尺度算法,建立两个自由纸面时,分别记为TA(NTSC)和TA′(NTSC);然后根据[UTC/UTCr-TA′(NTSC)]驾驭TA′(NTSC),得到RTA(NTSC),RTA(NTSC)是一个实时的受驾驭的纸面时间;然后,再根据[RTA(NTSC)-MC]和[UTC-MC](MC代表主钟信号)驾驭MC生成UTC(NTSC)。由于UTC(NTSC)定义为1PPS物理信号而不是纸面时,所以这里使用了两次驾驭[17]。如本文所述,假如UTC(NTSC)定义为纸面时,只需要1次驾驭即可。本文方法同样可以应用于建立UTC(NTSC)。不同于传统方法建立TA′(NTSC)时权重和预测值都相对于xi=TA′(NTSC)-hi计算得到,在本文方法中,权重和预测值都将根据xi=UTC/UTCr/喷泉钟/光钟-hi计算得到。因此,本文方法中不建立“自由”的纸面时,不存在因单台钟和TA相互影响而造成的不足。同时,本文方法可以针对每台钟分别优化设计预测算法和驾驭算法。
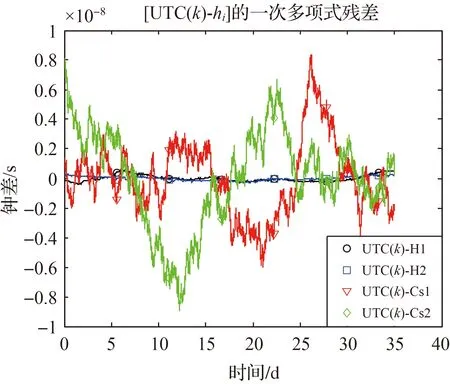
图9 [UTC(k)-hi]的残差Fig.9 Residuals of [UTC(k)-hi]
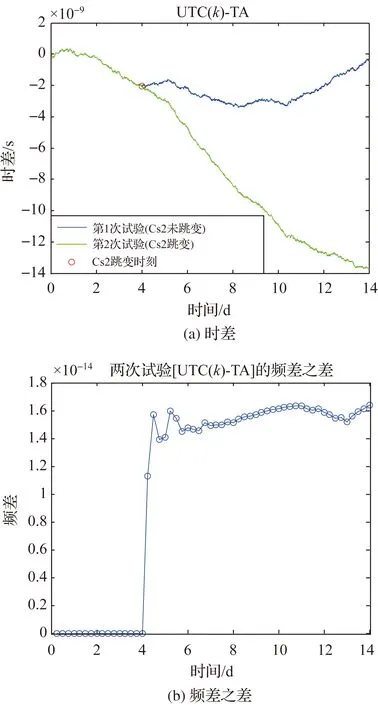
图10 [UTC(k)-TA]时差和频差之差的两次试验结果Fig.10 Two time differences and the difference of two frequency differences of [UTC(k)-TA]
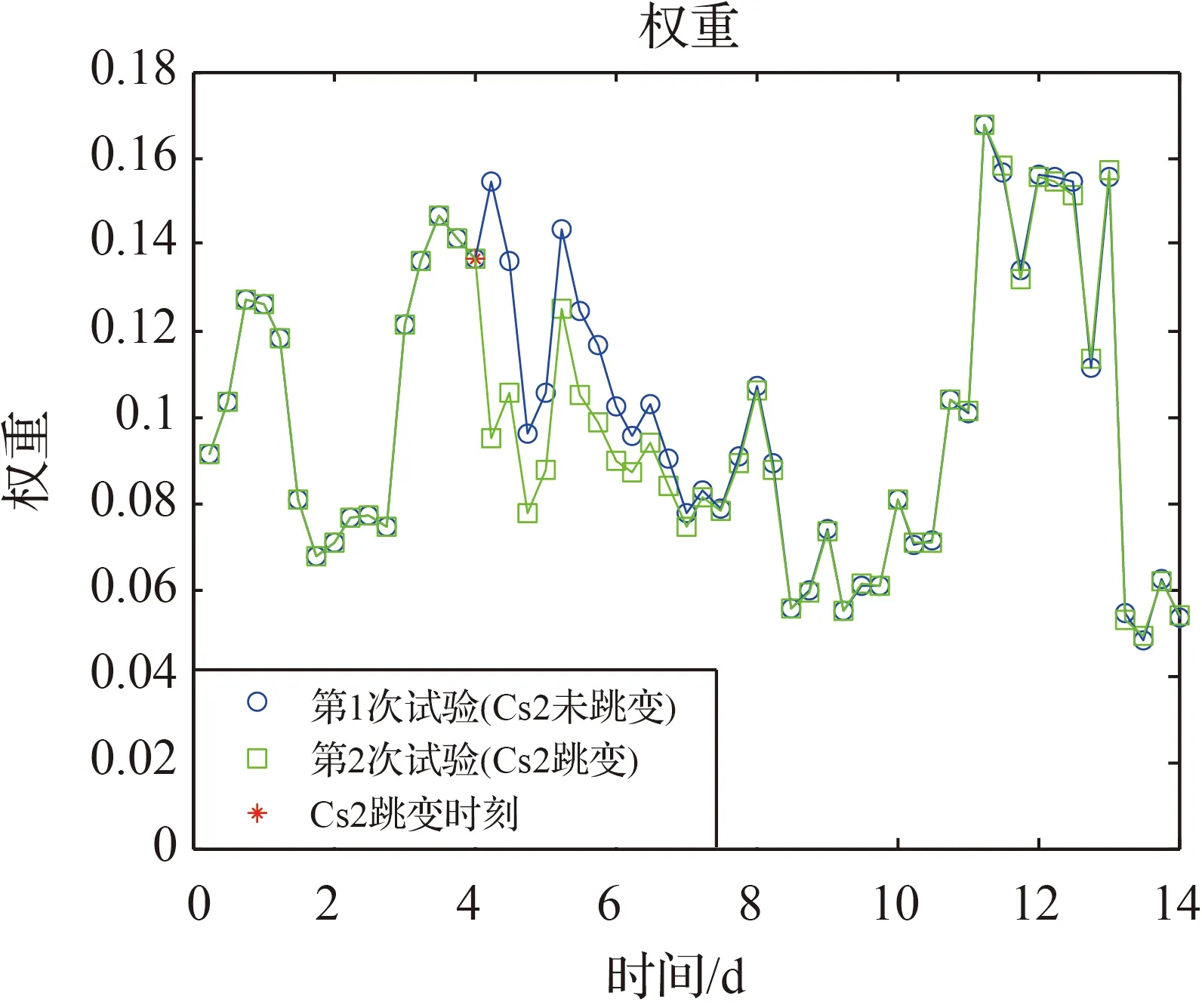
图11 两次试验中Cs2的权重Fig.11 Two experiment results of Cs2 weights
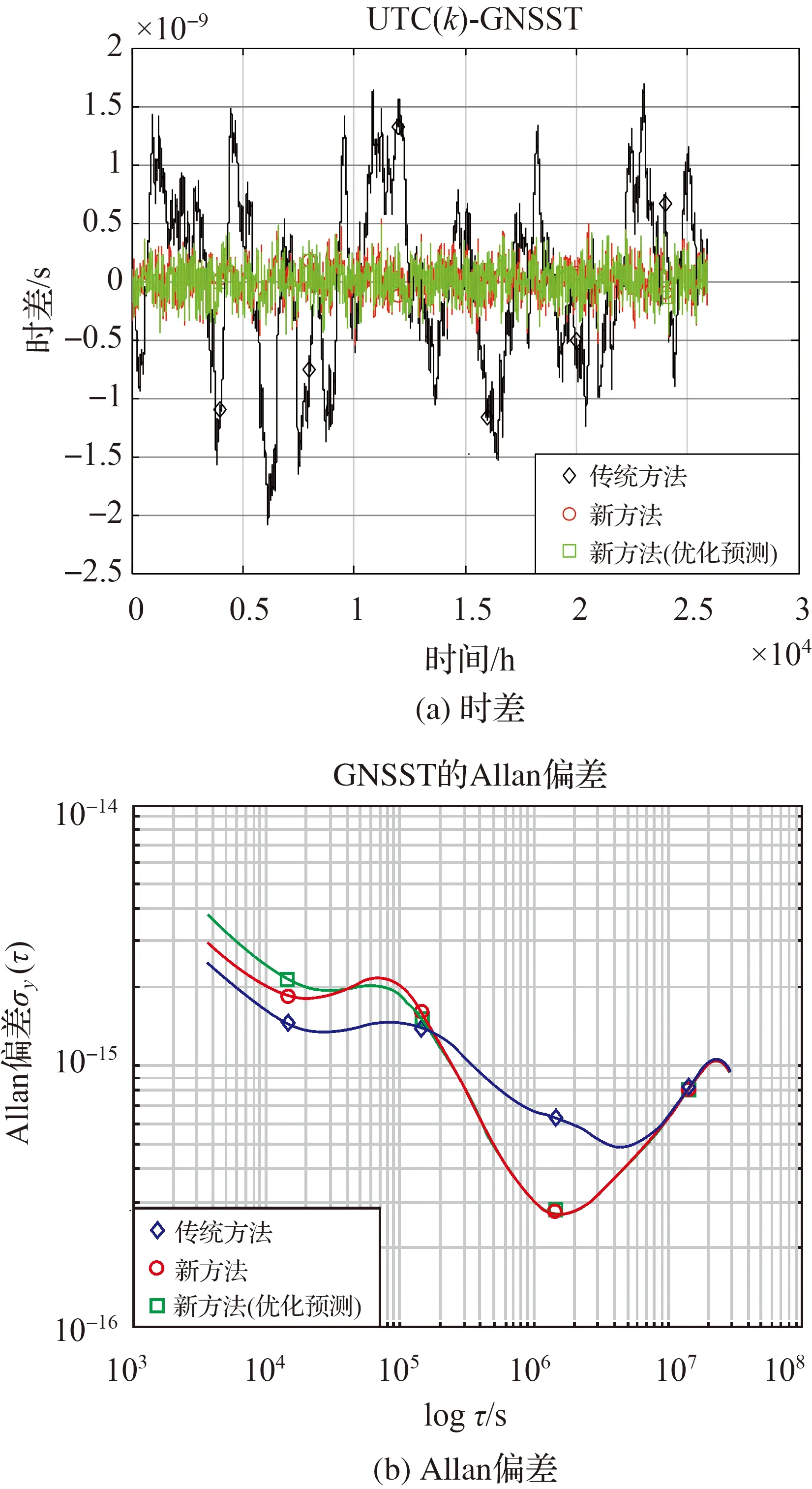
图12 3次试验的[UTC(k)-GNSST]的时差和GNSST的Allan偏差Fig.12 Time differences of [UTC(k)-GNSST] and Allan deviations of GNSST of three experiments
后续将在本文的基础上,结合BDS地面钟、星载钟配置,进一步优化本文方法的算法设计,并分析BDT的频率稳定度、频率准确度、时间同步精度、时间自主保持能力等性能。
