(2+1)维海森堡铁磁自旋链方程的怪波解及其局域性质

谭晓漫, 扎其劳

(内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022)

2014年,Latha等推导出一个新的(2+1)维海森堡铁磁自旋链方程[1]

(1)

其中,q是一个关于空间变量x,y和时间变量t的函数,a,b,c,d是磁耦合系数。该方程用来描述海森堡铁磁自旋链系统中非线性波传播,它也是非线性Schrödinger方程在(2+1)维的推广。通过特殊选择磁耦合系数a,b,c,d的值,方程(1)可表示为可积模型,拥有Lax对[2-3]和无穷多守恒律[3]。也可以通过Darboux变换方法[2-3]、Hirota双线性方法[4]、李群方法[5]以及符号计方算法[6-7]求解方程(1),并获得怪波解[2]、孤子解[3-4]、群不变解[5]、奇异解和周期波解等[5-6]。而目前关于方程(1)怪波解的局域分析和呼吸子解尚未被报道。因此,本文的重点是分析方程(1)怪波解的局域性质和求解呼吸子解。首先,利用符号计算方法构造(2+1)维海森堡铁磁自旋链方程(1)的怪波解；其次,通过分析怪波解的等高线[8],获得其局域化特征；最后,求得(2+1)维海森堡铁磁自旋链方程(1)的呼吸子解。

1 怪波解及其局域化特征

1.1 符号计算与怪波解

取方程(1)的种子解为q=e-idx,令其怪波解为

(2)

(3)

将(3)式代入(2)式,得方程(1)的有理函数解

(4)

当b=c=-d=1时,(2+1)维海森堡铁磁自旋链方程的解(4)在不同维度上的波形如图1所示。当限制维度为x=1,y=1和t=1时,图1中的(a),(b)和(c)分别为怪波和孤子。

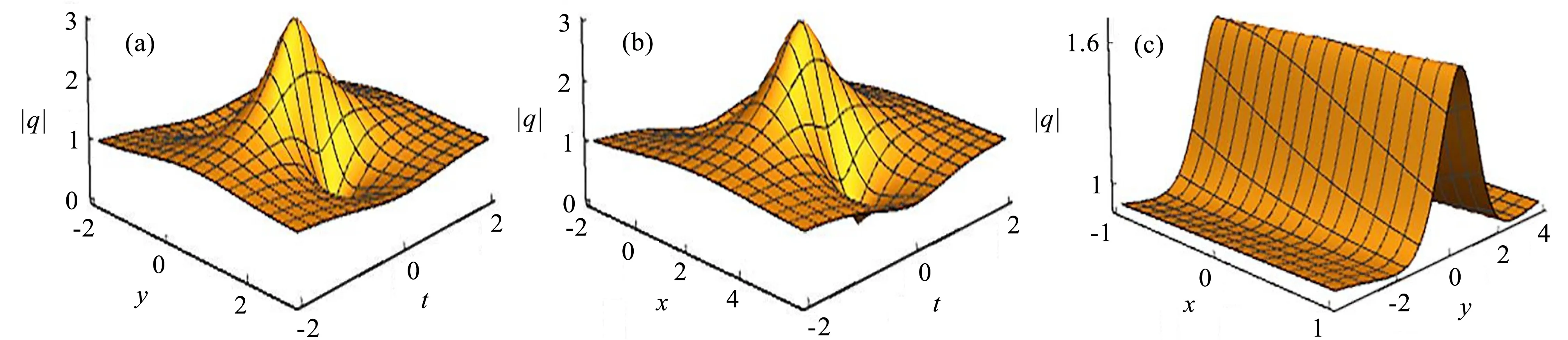
图1 x=1时的怪波(a)、y=1时的怪波(b)和t=1时的孤子(c),参数b=c=-d=1Fig.1 By selecting b=c=-d=1,(a) rogue wave with x=1; (b) rogue wave with y=1; (c) soliton with t=1

1.2 怪波解的局域化特征

情形1当x=1时,怪波解(4)可写成

(5)

128b2+64bc2d+8c4d2+64bc2d3+16c4d4-16b2H+64c3d3y+

64bcd2Hy+16c3d3Hy-32c3d5Hy+256bdy2-8bc2dH+

16bc2d3H-c4d2H+4c4d4H-4c4d6H+512b2d2t2+256bc2d3t2+

32c4d4t2-128b2d2Ht2-64bc2d3Ht2-8c4d4Ht2+64bc2d5Ht2+

16c4d6Ht2-256b2d4Ht4-128bc2d5Ht4-16c4d6Ht4+256bcd2y+

256bcd4Hyt2+64c3d5Hyt2+64c2d2y2+64bdHy2+16c2d2Hy2+

256bd3Hy2t2-96c2d4Hy2+64c2d4Hy2t2-128cd3Hy3-64d2Hy4=0。

(6)

(1) 当H=0时,等高线方程(6)化为双曲线

(7)

它的两条渐近线分别为

(8)

图2 密度图、双曲线(长虚线)、渐近线(短虚线)的组合(a)和双曲线(长虚线)、渐近线(短虚线)的组合(b),参数x=b=c=-d=1Fig.2 By selecting x=b=c=-d=1,(a) the combination of density plots,heyperbola (long dash line) and asymptotes (short dash line); (b) the combination of heyperbola (long dash line) and symptotes (short dash line)

(2) 当H=1时,等高线方程(6)化为凹的闭曲线

(9)

(10)

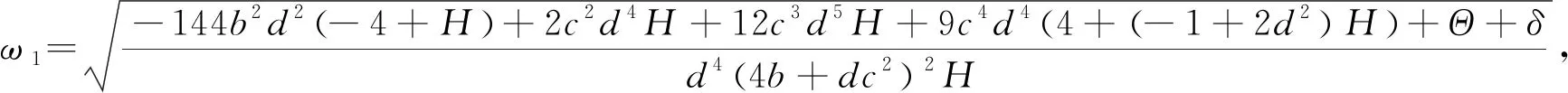
Θ=8bd3(H+6cdH+9c2(4+(-1+d2)H)),

其中

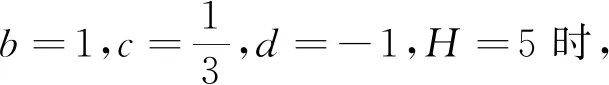
其中

Θ=8bd3(H+6cdH+9c2(4+(-1+d2)H)),

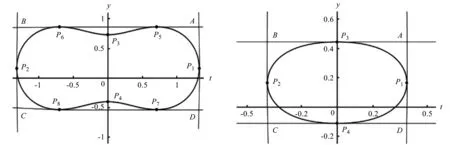
图3 等高线方程(6)在 图4 等高线方程(6)在 H=1时的凹的闭曲线 H=5时的凸的闭曲线 Fig.3 The concave curve of the contour plot (6) Fig.4 The convex curve of the contour plot (6)

图5 面积S(实线),长度L(长虚线)和宽度W(短虚线)Fig.5 The area S (solid line),the length L (long dot line) and width W (short dot line)

(11)

(12)

故

(13)

其中

Θ=8bd3(H+6cdH+9c2(4+(-1+d2)H)),

(14)

(15)

其中

ω4=4bd(4+H+4d2t2H),σ=c2d2(4+H+4d2t2H)。

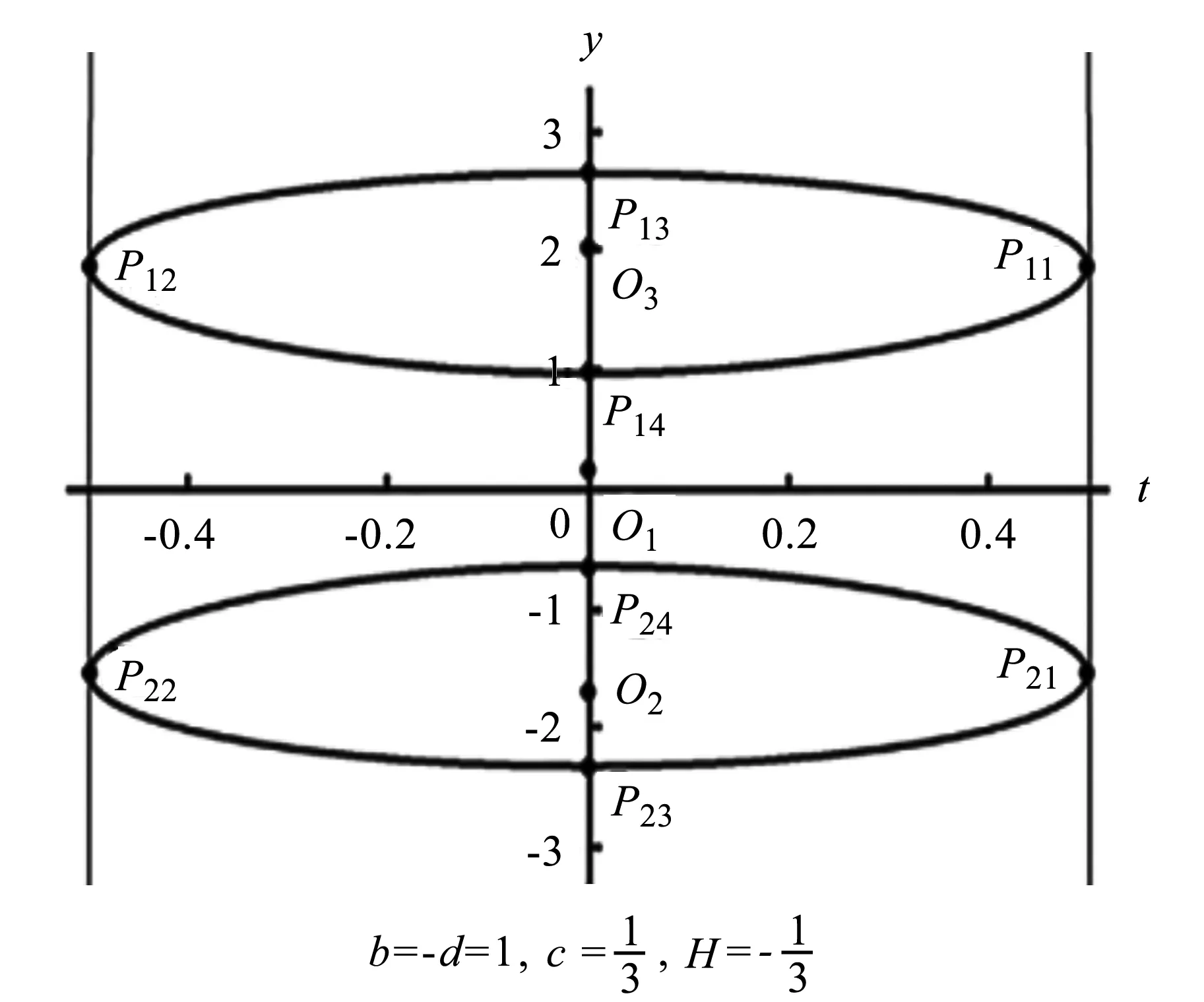
图6 等高线方程(6)的凸的闭曲线Fig.6 The convex curve of the contour plot (6)

P12P11平行于P22P21,y轴上的其他四个端点分别为

其中

并且有三个中心,分别为

图1(b) (y=1) 的情形类似情形1，故此处省略。

情形2当t=1 时,怪波解(4)可写成

(16)

128b2+64bc2d+512b2d2+8c4d2+256bc2d3+32c4d4-16b2H-

8bc2dH-128b2d2H-c4d2H-64bc2d3H-256b2d4H-8c4d4H-

128bc2d5H-16c4d6H+64bc2d3x2+16c4d4x2+16bc2d3Hx2+

64bc2d5Hx2+16c4d6Hx2-4c4d6Hx4+256bcd2xy+64c3d3xy+

64bcd2Hxy+16c3d3Hxy+256bcd4Hxy+64c3d5Hxy-32c3d5Hx3y+

256bdy2+64c2d2y2+64bdHy2+16c2d2Hy2+256bd3Hy2-

96c2d4Hx2y2-128cd3Hxy3-64d2Hy4+4c4d4Hx2+64c2d4Hy2=0。

(17)

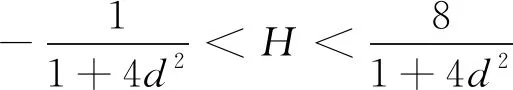
(1) 当H=0时,等高线方程(17)化为

128b2+64bc2d+512b2d2+8c4d2+256bc2d3+32c4d4+16c4d4x2+

256bcd2xy+64c3d3xy+256bdy2+64c2d2y2+64bc2d3x2=0。

(18)

(2) 当H=1时,等高线方程(17)可化为如下

(19)

(20)

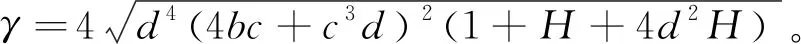
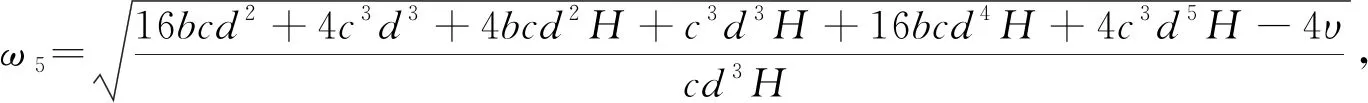
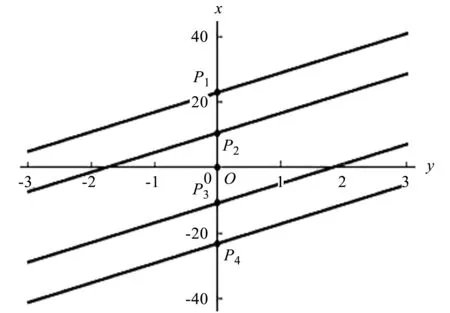
图7 等高线方程(17)在时的直线Fig.7 The lines of the contour plot (17) with

(21)

其中

ξ=16bcd2+4c3d3+4bcd2H+c3d3H+

16bcd4H+4c3d5H。

其中

ξ=16bcd2+4c3d3+4bcd2H+c3d3H+16bcd4H+4c3d5H。

2 呼吸子解

设方程(1)的呼吸子解的形式为

(22)

其中μ=gx+kt+ny,θ=hx+mt+ly。将方程(22)代入方程(1),令coshwμcossθsinhzμsinrθ同次幂系数为零,且ad=-1时,可得一个代数方程组,求解该代数方程组得到如下两组解:

(23)

(24)

其中b,c,d是任意参数。

将(23)式代入(22)式,得到Ma呼吸子

(25)

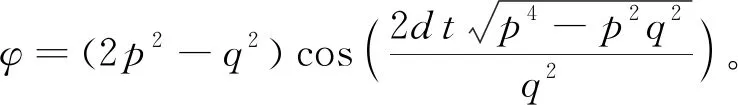
将(24)式代入(22)式,得到Akhmediev呼吸子

(26)

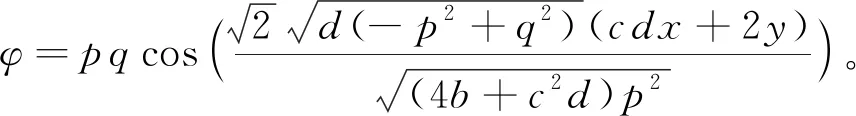
图8 x=1时的Ma呼吸子(a), y=1时的Ma呼吸子(b), t=1时的孤子(c),参数Fig.8 By selecting c=d=q=1, p=2, (a) Ma breather with x=1, (b) Ma breather with y=1, (c) soliton with t=1

3 结论

(2+1)维海森堡铁磁自旋链方程是著名非线性Schrödinger方程在(2+1)维的推广,本文首先研究了该方程的怪波解,并通过讨论怪波的等高线,分析了它的局域性质,揭示了怪波在不同的等高处的特性。其次研究了(2+1)维海森堡铁磁自旋链方程的两种呼吸子解,即Ma呼吸子与Akhmediev呼吸子。本文采取的计算机符号计算求解方法具有一定的普适性,可以应用到高维非线性方程中,有望获得更有意义的结果。