双势作用下玻色-爱因斯坦凝聚孤子的操控

王 艳

(长治学院电子信息与物理系,山西 长治 046011)

0 引言

近年来,对于玻色-爱因斯坦凝聚体(BEC)研究的热点之一就是量子操控,有关冷原子实验技术的不断提高实现了对各种不同形式的束缚外势的调控[1,2],可通过调节BEC中原子间相互作用或外部囚禁势阱来调控BEC的性质[3-6],比如:可以通过控制原子间相互作用的强弱,实现对BEC双孤子相互作用的操控[7]、通过调节周期性势阱的驱动频率和强度来控制孤子的位置[8]。另外还有利用超辐射散射实现对BEC动量的操控[9],以及通过调节原子有效质量,可以在不改变双阱势的前提下操控凝聚体[10]。

本文考虑通过控制外势场实现对BEC孤子的操控,关注的外势是双势,对双势参数的调节可实现对其强度、宽度和位置等的改变。数值模拟研究发现,BEC孤子在不同参数的双势中表现出不同的演化行为,因此可以通过控制双势实现对BEC孤子的操控。

1 理论基础

当凝聚体的横向尺寸与其修复长度具有相同数量级且比纵向长度小得多时,吸引的凝聚体孤子沿纵向的动力学可用一维的非线性薛定谔方程描述为

式中:ψ(t,x)是凝聚体波函数,V(x)是外势,这里考虑的是两个高斯势组成的双势,可以由两束激光形成,具体形式为

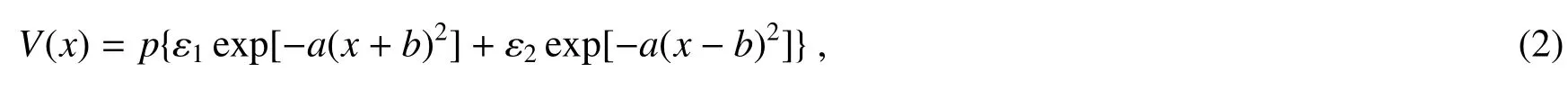
式中:p是外势的强度,参数a和b分别表示单个高斯势的宽度和位置。当参数ε1=ε2=1时,外势是双势垒;当ε1=ε2=-1时,外势是双势阱;当ε1=ε2=±1时,外势是混合势。在方程(1)和(2)中引入了无量纲变量而是横向谐振子长度,m是原子质量,ω⊥是横向谐振动角频率,as是s波散射长度[11]。此处所考虑的是一个在谐振子磁势阱中制备后被装入激光场中的BEC,磁囚禁势要远小于光学势,因此外势只保留了起主导作用的光学势。

2 数值模拟

2.1 单孤子在双势中的演化

考虑选取孤子形式为ψ(0,x)=ηsech[η(x-x0)]exp[iξ(x-x0)],其中η、x0、ξ分别表示孤子的振幅、中心位置和中心频率。选定孤子的参数η=1、x0=0、ξ=0.1,研究单孤子在双势中的演化行为。

当孤子处于双势阱中时有比较复杂的演化行为,其演化与双势阱的各参数密切相关,选取双势阱中单个势阱宽度的参数a=1,势阱强度参数p取不同的值时孤子的演化情况如图1～5所示,当p=0.1时,孤子能越过势阱,发生遂穿现象,结果显示在图1中;当p=0.2时,孤子会被单个势阱俘获,在被俘获的势阱内其振幅会有波动,使得孤子的演化过程呈现了很强的呼吸行为,孤子中心位置有小幅度波动,结果显示在图2中,可以通过改变势阱的位置参数b来控制孤子的位置;当p=1.5时,孤子在两势阱之间摆动,结果显示在图3中;当p=1.7时,孤子又越过了势阱,发生遂穿现象,与p=0.1时不同的是势阱最深的区域是孤子的禁区,孤子在穿越势阱时是一种“幽灵式”的遂穿,结果显示在图4中;当p=2.5时,孤子又能被势阱俘获,与p=0.2时不同的是势阱最深处是孤子的禁区,BEC孤子被分裂成两组分,而且孤子的演化过程呈现了一定的呼吸行为,结果显示在图5中。外势参数a既表示高斯势的宽度也表示势阱壁的陡峭程度,当a越大时势阱壁越平缓,孤子越容易越过势阱,发生遂穿现象;当a越小时势阱越窄,孤子也越容易越过势阱,发生遂穿现象,如图6所示。

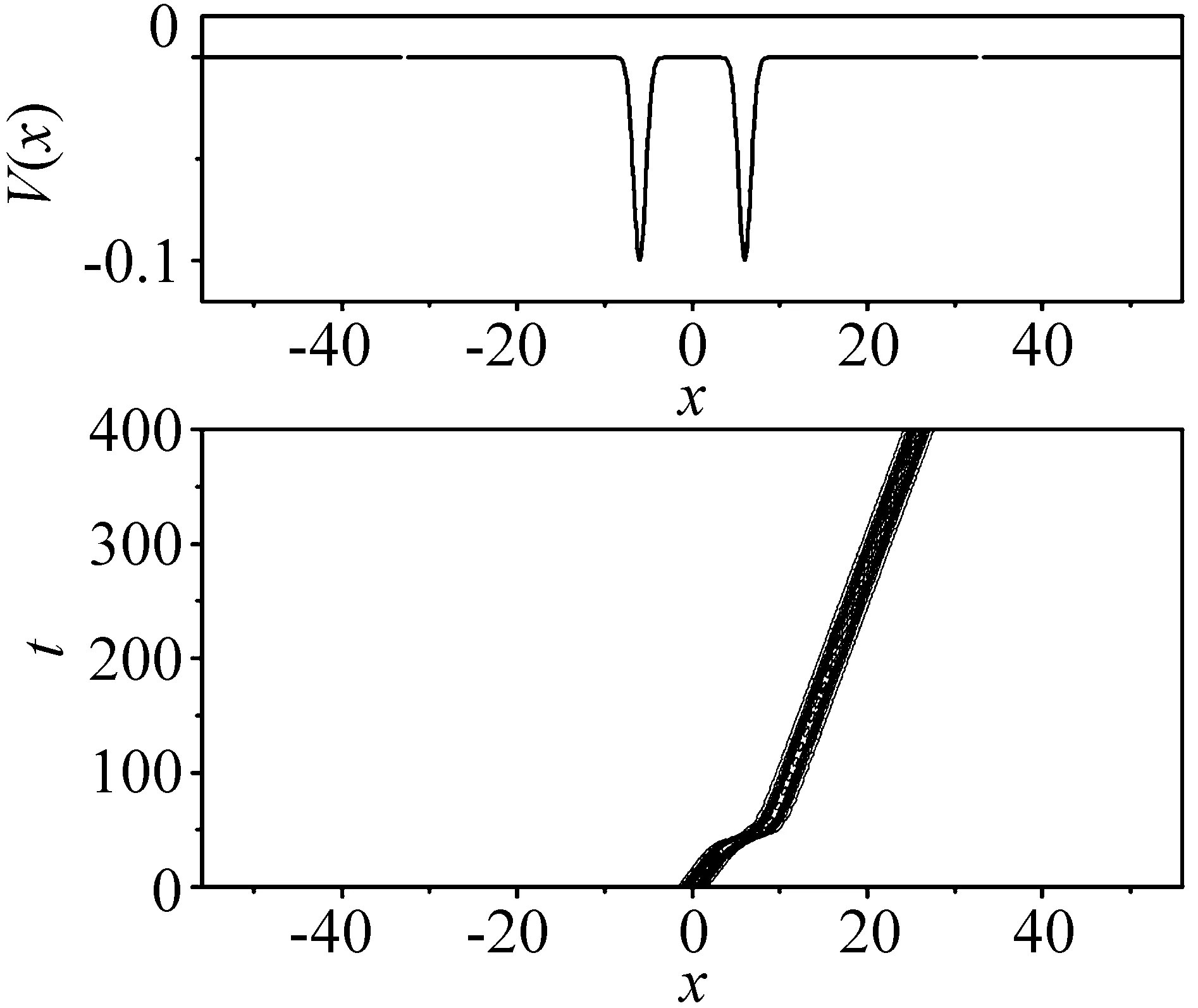
图1 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=0.1,ε1= ε2=-1,a=1,b=6Fig.1 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η =1,x0=0,ξ=0.1,p=0.1,ε1= ε2=-1,a=1,b=6

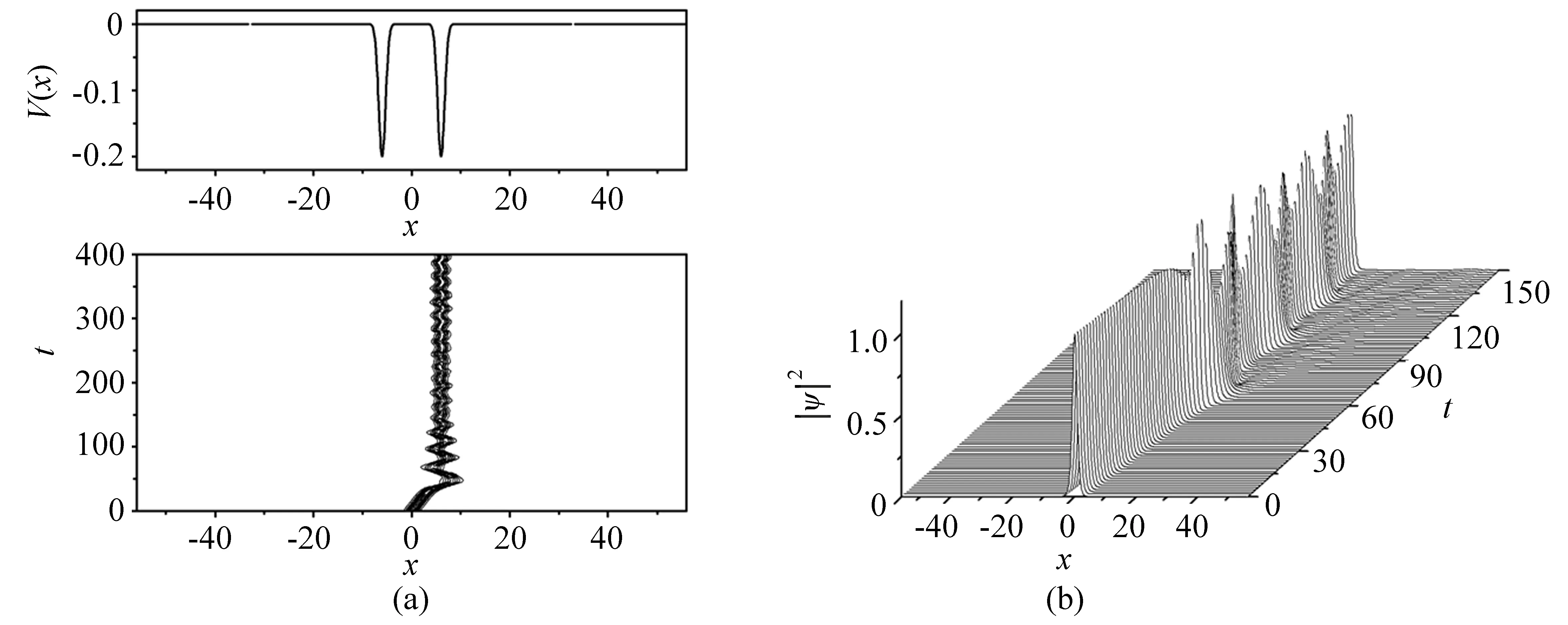
图2 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=0.2,ε1=ε2=-1,a=1,b=6。(a)等高线图;(b)三维曲面图Fig.2 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=0.2,ε1= ε2=-1,a=1,b=6.(a)Contour plot;(b)3D surface

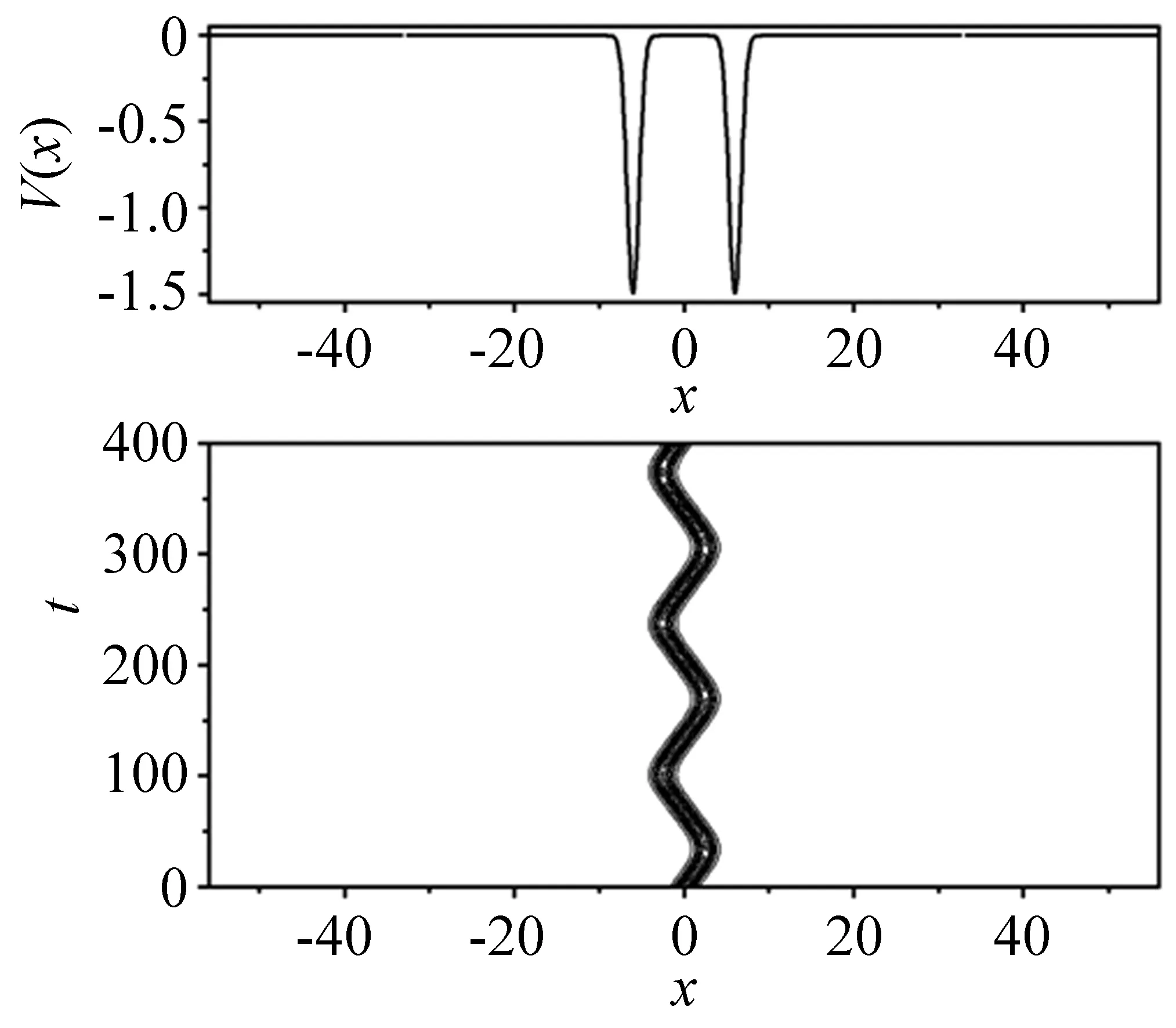
图3 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=1.5,ε1=ε2=-1,a=1,b=6Fig.3 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=1.5,ε1= ε2=-1,a=1,b=6

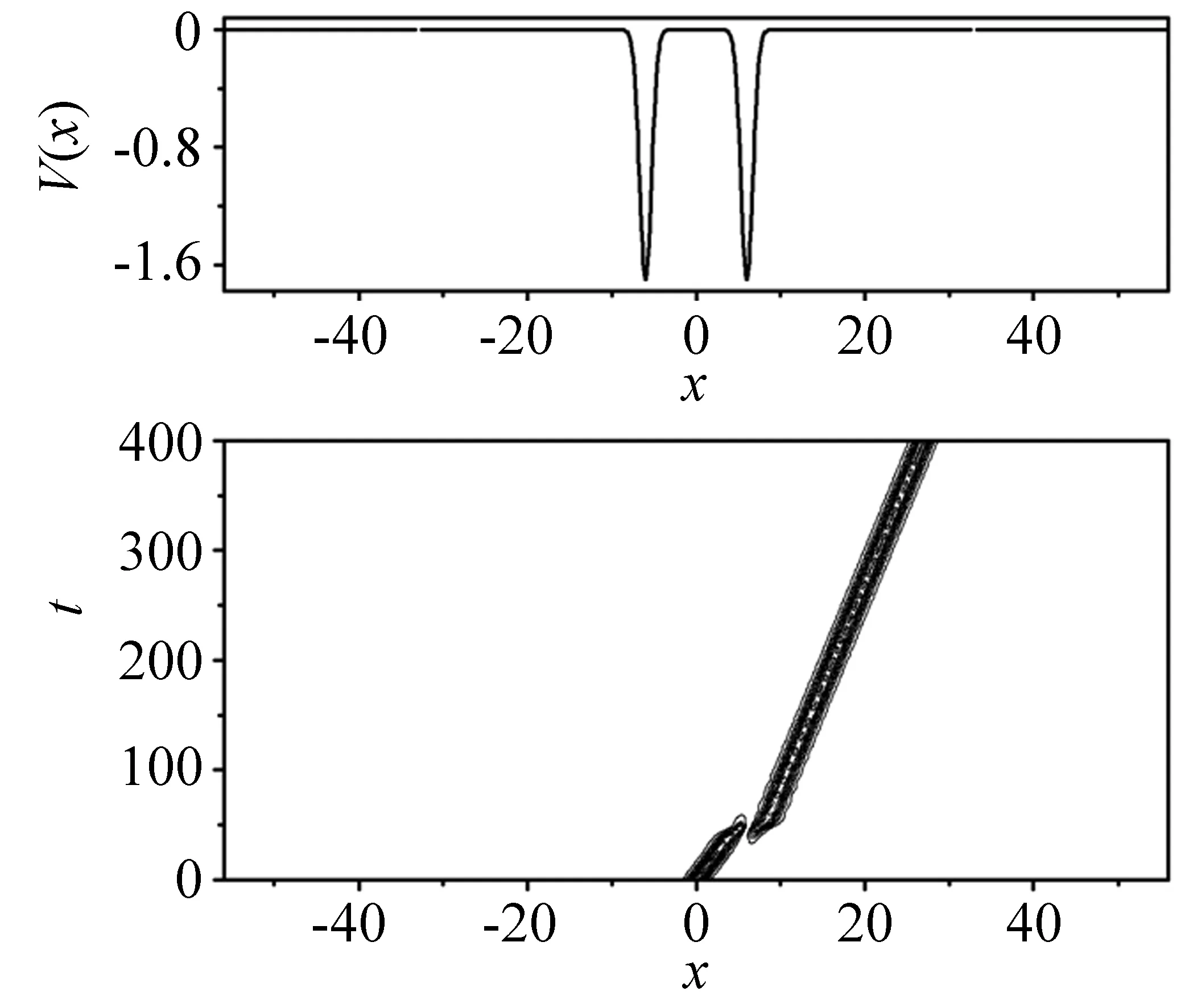
图4 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=1.7,ε1=ε2=-1,a=1,b=6Fig.4 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=1.7,ε1= ε2=-1,a=1,b=6

图5 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=2.5,ε1=ε2=-1,a=1,b=6。(a)等高线图;(b)三维曲面图Fig.5 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=2.5,ε1= ε2=-1,a=1,b=6.(a)Contour plot;(b)3D surface

图6 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=0.2,ε1=ε2=-1。(a)a=0.05,b=20;(b)a=20,b=6Fig.6 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=0.2,ε1= ε2=-1.(a)a=0.05,b=20;(b)a=20,b=6

考虑外势强度参数p=0.2,当孤子处于双势垒中时,演化结果如图7所示,孤子在双势垒之间摆动,从图7与图2和图6的比较可知,与在双势阱中相比孤子更难穿越势垒,当然如果双势垒的强度参数p比较小或者孤子的中心频率参数ξ较大,孤子也能穿越势垒,发生遂穿现象;在势阱和势垒组成的混合势中,选择合适的外势宽度参数a=1,不论孤子参数ξ=0.1或ξ=-0.1,孤子都能被势阱俘获,结果如图8所示,这样更方便操控孤子的位置。

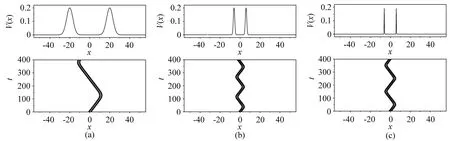
图7 双势中BEC孤子的演化,其中参数为:η=1,x0=0,ξ=0.1,p=0.2,ε1=ε2=1。(a)a=0.05,b=20;(b)a=1,b=6;(c)a=20,b=6Fig.7 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,ξ=0.1,p=0.2,ε1= ε2=1.(a)a=0.05,b=20;(b)a=1,b=6;(c)a=20,b=6

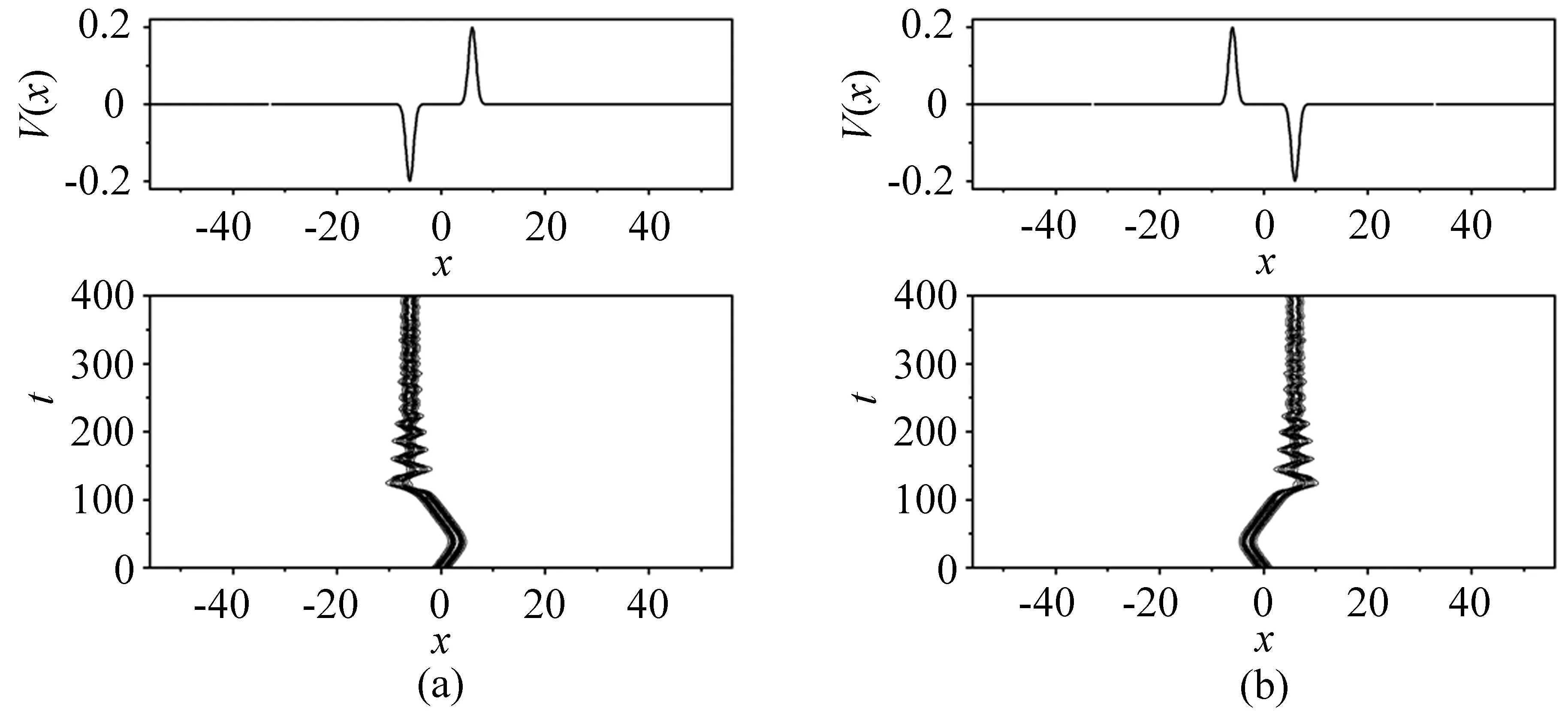
图8 双势中BEC孤子的演化,其中参数为:η=1,x0=0,p=0.2,a=1。(a)ξ=0.1,b=6,ε1=-ε2=-1;(b)ξ=-0.1,b=6,ε1=-ε2=1Fig.8 Evolution of the BEC soliton in double potentials,here the parameters are as follows:η=1,x0=0,p=0.2,a=1.(a)ξ=0.1,b=6,ε1=-ε2=-1;(b)ξ=-0.1,b=6,ε1=-ε2=1

2.2 双孤子在双势中的演化

考虑两个等振幅且中心频率为0的孤子形式ψ(0,x)=sech(x-x0)+sech(x+x0),其中2x0为孤子的初始间距。当双孤子的初始间距2x0=20时,考虑外势参数p=0.2、a=1的情况,在双势阱中的演化如图9所示,两孤子可能会被两个势阱各自俘获;在双势垒中的演化如图10所示,若两孤子在双势垒的外侧,就会相互远离,若两孤子在双势垒的内侧,就会发生相互作用。总之,势阱吸引孤子,势垒排斥孤子。

图9 双势中两个BEC孤子的演化,其中参数为:p=0.2,ε1=ε2=-1,x0=10,a=1。(a)b=6;(b)b=14Fig.9 Evolution of two BEC solitons in double potentials,here the parameters are as follows:p=0.2,ε1= ε2=-1,x0=10,a=1.(a)b=6;(b)b=14

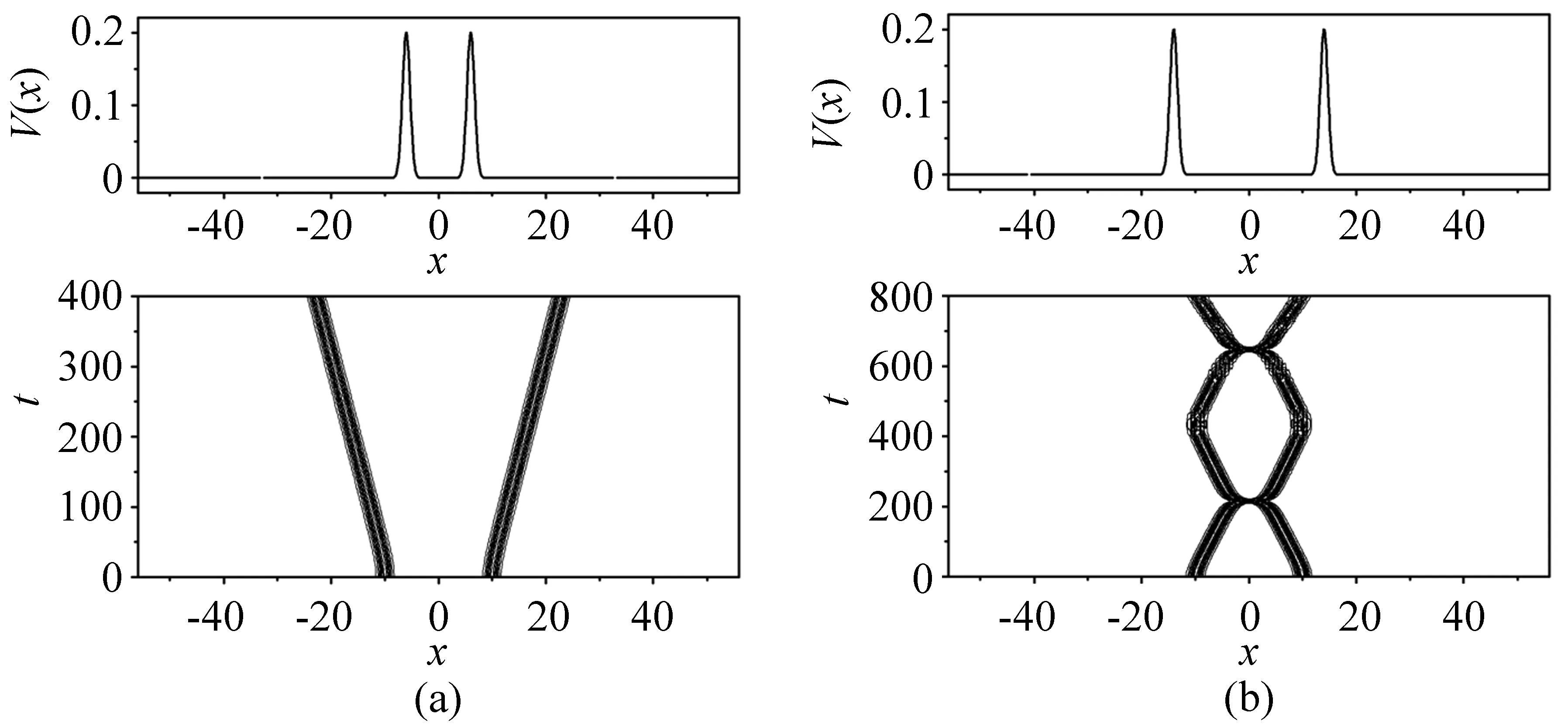
图10 双势中两个BEC孤子的演化,其中参数为:p=0.2,ε1=ε2=1,x0=10,a=1。(a)b=6;(b)b=14Fig.10 Evolution of two BEC solitons in double potentials,here the parameters are as follows:p=0.2,ε1= ε2=1,x0=10,a=1.(a)b=6;(b)b=14

3 结论

操控和管理势场中的BECs是BEC动力学中的重要问题,讨论了在双势作用下BEC孤子的动力学演化。孤子在双势阱的作用下表现出比较复杂的演化行为,有摆动、遂穿、被势阱俘获;可以利用BEC孤子在势阱和势垒中不同的演化行为,设计出混合势来操控BEC孤子,可准确控制其位置,为与BEC孤子操控相关的宏观量子现象的应用提供依据。