基于Hardy-type佯谬的混合态高概率量子非局域关联检验*

刘晋 缪波 贾欣燕 樊代和

(西南交通大学物理科学与技术学院,成都 610031)

量子非局域关联是量子力学预言的重要现象,同时也是量子理论区别于经典理论的重要特征之一.因此,对量子非局域关联的高成功概率检验有着重要意义.本文提出了一种基于Hardy-type佯谬的、可用于针对纯态和混合态进行高成功概率量子非局域关联检验的逻辑,并对其适用性进行了证明.研究发现,利用本文提出的检验逻辑对量子纯态进行量子非局域关联检验,成功检验概率将随着量子纯态的纠缠度增加而出现先增大后减小的现象,最大的成功检验概率超过39%.进一步利用提出的检验逻辑,以Werner态这种量子混合态为例,进行了针对混合态的量子非局域关联的高概率检验研究.研究发现,随着混合态的纯度增加,成功进行量子非局域关联检验的概率也将增加.最后给出了针对Werner态这种量子混合态进行高成功概率量子非局域关联检验的条件和范围.

1 引 言

1935 年,Einstein,Podolsky和Rosen三人[1]提出了著名的关于量子力学完备性的讨论,即EPR佯谬.他们认为量子力学是一套不完备的理论,即量子力学预言存在着量子非局域关联的现象.因此,量子非局域关联被认为是量子力学最典型也是最重要的特征之一,同时也是量子力学区别于经典物理的重要现象之一.同时,量子非局域关联还对量子信息进程的实现具有重要意义,因此对量子非局域关联的检验不论从理论还是实验研究显得至关重要.

目前对于量子非局域关联的检验常用的有两类方案：一是通过对Bell不等式的违背来检验量子非局域关联,另外一类则是无不等式的检验方案来检验量子非局域关联.1964年,Bell[2]提出一个满足局域隐变量而在量子力学中是违背的不等式来说明没有任何的局域实在论能重复量子力学的预测,从而验证了量子非局域关联的存在.1969年,Clauser,Horne,Shimony和Holt四人[3]在Bell不等式的基础上,提出了两比特的更加便于实验验证量子非局域关联的CHSH-Bell不等式,并且在实验上得到了验证[4].1990年,Greeberger,Horne,Zeilinger[5]提出的GHZ佯谬是关于量子非局域关联的无不等式证明,然而其只适用于大于等于三粒子的系统.1993年,为了证明两粒子系统的量子非局域关联,Hardy[6]提出了两粒子情况下的佯谬,该证明表面仅只有一阶梯子的情况下,可以获得违反局域隐变量理论的最大概率约为9%.基于Hardy佯谬,通过对两比特纠缠态的单次联合测量,即可在无统计不等式的情况下验证量子非局域关联,因此Hardy佯谬也被认为是“Bell定理的最佳的版本”[7].尽管利用Hardy佯谬检验量子非局域关联的概率非常低,但是足以证明量子非局域关联的存在.之后学者将Hardy佯谬推广到K阶梯子的量子非局域关联的证明,当 K→∞时,最大概率可达到50%[8].后来,通过许多量子态,例如通过利用光子对的偏振纠缠态[9-11],轨道角动量纠缠态[12,13]以及能量-时间纠缠态[14],实验结果均证明了量子非局域关联现象的存在,违背了经典理论的预测.后来,学者们又将Hardy佯谬推广到了多粒子[15,16]和多维[17]的系统中,并且成功地检验了量子非局域关联现象.然而,值得关注的是,到目前为止,上述提到的大多数关于量子非局域关联检验的研究,均是以量子纯态作为为研究对象的.

从实验角度而言,由于受到各种实验不完美因素的限制,实验制备的量子态往往是一个量子混合态.因此,利用量子混合态来进行量子非局域关联的检验就具有重要的现实意义.目前,针对量子混合态进行的量子非局域关联检验的研究中,文献[18]将原始量子非局域关联检验的相关证明推广到一类特殊的混合态,给出了一个满足混合态量子非局域关联检验的必要条件.文献[19]将原始的量子非局域关联的严格证明进行改进和推广,将一些典型的混合态进行了量子非局域关联的相关研究,改进了文献[18]中的结果,但是其不利于进行实验的验证.尽管文献[20]提出了一种基于混合态的量子非局域关联检验更优的条件,但是成功检验概率较小,不利于进行实际的实验检验.

本文研究了一种适用于量子混合态[21,22]进行Hardy-type佯谬的逻辑,这种逻辑可以以较高的成功概率来进行针对量子混合态的量子非局域关联检验.首先,本文介绍了提出的可适用于量子混合态的高概率Hardy-type佯谬逻辑,并证明了其正确性；其次,证明了提出的检验逻辑也能适用于纯态的量子非局域关联检验的情况；最后,本文以Werner态[23]这种量子混合态为例,进一步研究了进行量子非局域关联检验的条件等.

2 适用于量子混合态的Hardy-type佯谬高概率检验逻辑

受文献[24]启发,我们以两比特态的量子态为基础,首先给出可用于混合态的高概率Hardytype佯谬检验逻辑.考虑由自发参量下转换所产生的信号光(s)和闲置光(i),选取相应的测量基对信号闲置光子进行偏振联合测量.用 P(αs,βi) 表示测得s光子的偏振在 αs方向和i光子的偏振在βi方向的联合测量概率.由于s光子与i光子的偏振测量概率可看作两个独立的事件,因此可以得到：定义则有：

假设通过选取合适的测量基 {αms,βni},可使得(3)—(5)式同时满足：

在满足(2)式的情况下,受(3)—(5)式条件的约束,可以证明能够得出如下两个结论.

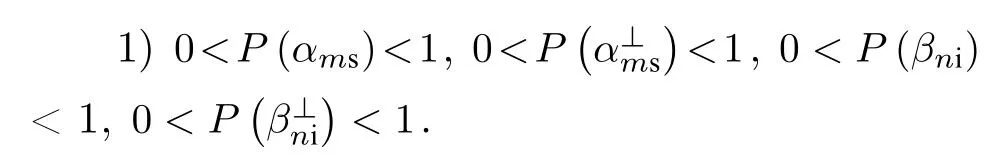
证明由(2)式可知,s光子的偏振与i光子的偏振必定不在α1s和 β1i方向,即 P(α1s)／=1 与则代入(3)式后可得到此结果不能满足(5)式.因此可以得出若s光子偏振在方向,即那么根据(3)式有P(α2s,则此结果不能满足(5)式,因此s光子偏振必定不在方向,即若i光子偏振在方向,即根据(3)式有则此结果不能满足(5)式,所以i光子偏振必定不在方向,即根据以上分析,可得

由于上面已经得出 0＜P(α1s,β1i)＜ 1 ,则根据(3)式可以得出因此s光子的偏振与i光子的偏振必定不在和 β2i方向上,即若s光子偏振在 α2s方向,即 P(α2s)=1 ,根据(5)式可得到P(α1s,β2i)=1,则不能满足(3)式,因此s光子偏振不在 α2s方向,即若i光子偏振在方向上,即根据(5)式有则不能满足(3)式,因此i光子的偏振不能在方向上,即因此可以得出：0＜P(α2s)＜ 1 ,

通过如上的分析,可以汇总得出如下的结论：

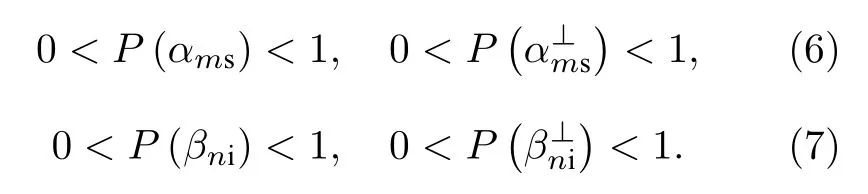
2) 在满足(2)式的情况下,经典局域关联将导致 H3＜ 1.

证明定义(8)—(10)式为：

由(3)(式与)(1a)式以及(8)式相结合可得P(β1i)+P=1+H4＞ 1,进一步与(1b)和(7)式相比较可得到

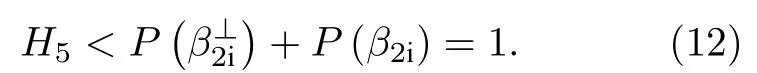
从以上证明得到的两个结论中可以看出,在经典局域关联下,如果选取的测量基能够同时满足(3)—(5)式,则(2)式必定不能成立,即

然而,在量子力学非局域关联理论中可以证明,在选取的测量基能够同时满足(3)—(5)式时,却可以得到的结论.因此,通过检验概率H值是否大于0,就可以检验量子非局域关联是否存在.并且H值越大,则对于量子非局域关联检验的概率越高,量子非局域关联现象越明显.

3 基于Hardy-type佯谬的高概率量子非局域关联检验

下面首先来证明上述提出的高概率Hardytype佯谬检验逻辑,针对量子纯态中也是适用的.对于两比特偏振纠缠纯态,其波函数可表示为

其中,|H〉表示水平偏振态,|V〉表示垂直偏振态,r (0≤r ≤1)值的大小决定了(15)式所示的量子纯态的纠缠度.例如,当 r =1 时,(15)式为最大纠缠态.

当使用如下所示的通用测量基 |φ〉M,

作用于(15)式,则可以计算得出相应的联合测量概率为

此时,利用Mathematica程序,可以计算得出在满足(3)—(5)式的条件下(即H1= H2= H3=可以获得的最大概率值 Hmax.图1显示了 Hmax随r 的变化关系.

从图1中可以看出,对于如(15)式所示的量子纯态,量子非局域关联的成功检验概率会随着r 值的增大先增大后减小.特别地,当r =0.773066时,可获得最大的 Hmax值,即量子非局域关联检验的最大概率为此时对应的测量基分别为：α1s=0.722166 ,α2s=1.50353 ,β1i=1.11185,β2i=0.305655.该结果与文献[24]利用纯态进行的量子非局域关联检验得到的结果一致,证明了提出的关于Hardy-type佯谬检验量子非局域关联的有效性.与原始的Hardy佯谬检验方案成功概率约9%相比[6],利用本文提出的逻辑,可将量子非局域关联检验的成功概率提高到约39.1%,因此本文提出的基于Hardy-type佯谬逻辑,可极大地提高进行量子非局域关联检验的成功概率.值得注意的是,当 r＜ 0.378525 或r＞ 0.778883时,由于(3)—(5)式无法被同时满足,因此对这些范围内的量子纯态,无法用本文提出的逻辑进行量子非局域关联的检验.

图1 Hmax随r 的变化Fig.1.Relationship between Hmax and r.

进一步重点研究关于混合态的高概率量子非局域关联检验.具体而言,以Werner态这种量子混合态为例,利用本文提出的Hardy-type佯谬检验逻辑,分析量子混合态的量子非局域关联检验情况.

对于量子混合纠缠态Werner态,其密度矩阵可写为[23]

其可认为是如(15)式所表示的非最大纠缠纯态|ψ〉混合了一定的白噪声(0≤t＜ 1)所得到.其中I表示单位矩阵.本文通过的值来判定该混合态的混合程度,即当对应纯态,则是对应混合态.Tr(ρ2)的值越高,Werner态越接近于量子纯态.

对于如(18)所描述的量子混合态,当用如(16)式所示的通用测量基进行联合概率测量,可计算得到如下式所示的联合测量概率：

同理,利用(19)式,可以计算得出在满足(3)—(5)式的条件下(即 H1=H2=H3=1),可以获得的最大概率值 Hmax.特别地,在 r =0.773066 (此情况下,Werner态中所含纯态部分(即当 t =1 时的情况)可获得最大概率的量子非局域关联检验)和 r =0.599997 (此情况下,下文可证明所对应的Werner态,满足量子非局域关联的检验的条件范围是最大的)两种情况下,如(18)式所示的量子混合态,基于本文提出的Hardy-type佯谬的量子非局域关联检验成功概率以及 Tr(ρ2) 随参数t 的变化关系如图2所示.

从图2中可以看出,利用本文提出的Hardytype佯谬逻辑,不论r 值处于哪种情况,随着t 参数值的增大(即混合态越来越接近纯态),检验量子非局域关联的成功概率都将越增大.从图2(a)中可以看出：当 r =0.773066 时,用(18)式所示的混合纠缠态进行量子非局域关联检验,仅当满足t ≥0.982327(此时 Tr(ρ2)≥0.973725)时,该混合态才能利用本文提出的检验逻辑进行量子非局域关联检验,但成功检验的概率较大,为 Hmax=0.33782 ,且随着t 的增大而非线性增大.特别地,当t =1(即纯态)时,Hmax=0.391179 ,该结果与文献[24]利用纯态检验得到的结果一致.从图2(b)中可以看出：当 r =0.599997 时,用(18)式所示的混合纠缠态进行量子非局域关联检验,当满足t ≥0.912649(Tr(ρ2)≥0.874696)时,该混合态就能利用本文提出的检验逻辑进行量子非局域关联检验,但成功检验的概率为 Hmax=0.172799 ,且随着t 的增大而非线性增大.特别地,当 t =1 (即纯态)时,Hmax=0.261343.与图2(a)所示的情况相比,尽管图2(b)中所用的参数可用于成功检验量子非局域关联的范围更大,但其缺点是成功检验的概率要稍低一些.但不论如何,利用本文提出的Hardytype佯谬检验逻辑,都能以较大的成功概率检验量子非局域关联.

图2 Tr(ρ2) 以及 Hmax随t 参数的变化关系 (a) r =0.773066 的情况；(b) r =0.599997 的情况；其中蓝色实线表示 Hmax随t 的变化关系,对应于右边纵坐标；黑色点化线表示 Tr(ρ2) 随t 的变化关系,对应于左边纵坐标Fig.2.Relationship between Tr(ρ2) and Hmax with t.The blue solid line means Hmaxvs.t ,using the right longitudinal coordinates.The black dot dash line means Tr(ρ2) vs.t using the left longitudinal coordinates.Fig.2 (a) is the situation of r =0.773066 and Fig.2 (b) is the situation of r = 0.599997.

值得注意的是,利用本文提出的Hardy-type佯谬检验逻辑,针对如(18)式所示的混合态,尽管可以以较高的成功概率进行量子非局域关联的检验,但是,从上面的分析也可以看出,只有满足一定条件(即混合态的纯度必须要大于某一个值,以及r 的取值必须在某一范围)的混合态才能(即能找到一定的测量基可使得条件H1=H2=H3=1能够被同时满足)进行量子非局域关联的检验.因此,图3给出了利用本文提出的Hardy-type佯谬检验逻辑,可对如(18)式所示的混合态成功进行量子非局域关联检验的范围.

从图3中可以看出,对(18)式所示的混合态而言,仅当在满足条件：0.378525≤r ≤0.778883时,该混合态才能利用本文提出的Hardy-type佯谬检验逻辑成功地进行量子非局域关联检验.而且,对于某一固定的r 值,(18)式所示混合态的纯度也必须进一步满足一定条件(即存在t 参数的最小值 tmin),才能成功地进行量子非局域关联检验.例如,当 r =0.599997 时,(18)式所示的混合态具有最大的条件范围进行量子非局域关联的检验.即只要混合态的纯度满足条件 t ≥0.912649 (此时对应的 Tr(ρ2)≥0.874696),就能成功地进行量子非局域关联检验.

图3 tmin随r 的变化Fig.3.Relationship between tmin and r.

4 结 论

提出了一种适用于任意两比特纠缠混合态的Hardy-Type佯谬检验逻辑,该逻辑可以较高的概率成功地检验量子非局域关联.首先,利用偏振联合概率测量的方法,证明了该检验逻辑的适用性.在此基础之上,以两比特偏振纠缠纯态为例,证明了该检验逻辑也能适用于量子纯态的情形.结果表明,对纠缠纯态而言,该检验逻辑可获得的成功检验概率随着r 的增加将出现先增大后减小的情形,最大成功检验概率可从传统的约0.09提高到约Pmax=0.391179.其次,本文以Werner态这种混合态为例,从理论上分析了当Werner态中的参数r 和t 改变时,该混合态进行量子非局域关联检验的情形.研究结果表明,对于固定r 值的混合态,纯度越高(即 Tr(ρ2) 越接近1),则其成功检验量子非局域关联的概率越大.最后,本文也研究了针对Werner混合态的成功检验量子非局域关联的t 参数范围.结果表明,当 r =0.599997 时,可用于量子非局域关联检验的混合态的范围最大,即只需t＞ 0.912649即可.由于本文提出的检验逻辑针对量子混合态,可以较大的成功概率检验量子非局域关联,因此该方法更加有利于实验的验证.