关于σ-空间的基和极小基

杨雯澜，李进金，张呈玲

（闽南师范数学与统计学院，福建漳州363000）

1997年，Ákos[1]首先给出了广义拓扑(generalized topology)的定义，设X是非空集合，g是X的一个子集族，如果g满足：1)∅∈g;2)g中元素对任意并满足封闭性，则称g是X上的广义拓扑，称(X，g)是广义拓扑空间.此后Ákos 等[2-5]对广义拓扑展开了研究.2013年，Kim 等[6]在广义拓扑的基础上定义了σ-结构，设X是非空集合，σ是X的子集族，如果σ中的元素对于任意并满足封闭性，则称σ是X上的一个σ-结构，称σ中的元素为σ-开集，称(X，σ)为一个σ-空间.Kim 等[6-8]在σ-开集的基础上讨论了σ-结构的一些性质，2017年黄丽[9]给出了σ-子空间、σ-连续映射、(σ1，σ2)-连续映射的定义.而在拓扑空间中基是非常重要的概念，对于拓扑空间基和子基的简化问题的讨论一直受到很多学者的关注.文献[10]给出了拓扑空间基的定义，2011年Khayyeri 等[11]定义了广义拓扑空间的基，文献[12]给出了LF拓扑空间基的定义.本文在前人研究基础上，定义了σ-空间中的基和极小基，并探讨其相关性质.

不难发现，σ-结构不一定在有限交下封闭且σ-结构中任意并封闭的条件与拓扑结构并封闭的条件不同：设σ是X上的一个σ-结构，则空集不一定属于σ.那么σ-空间中基的定义与拓扑空间中基的定义有什么联系?拓扑空间中基的相关性质在σ-空间中是否适用?此外，一个拓扑空间可以有多个不同的基，而基又能生成唯一的拓扑，那么σ-空间的基能否生成唯一的σ-结构?另一方面，文献[13]指出在一般拓扑空间的基ℬ是极小的当且仅当ℬ中不存在并可约元，那么这一结论在σ-空间中是否适用?此外，Stong[14]指出每个有限拓扑空间都存在唯一的极小基，但这一结果还未推广到σ-空间.受以上启发，对σ-空间中的概念进行推广，给出了σ-空间中的基以及极小基的概念.下面针对上述提出的相关问题，进行具体探讨，得到了一些结果.

1 预备知识

首先，对本文中的一些记号进行简要说明.设X为非空集合，(X，σ)表示一个σ-空间，σ-空间的基记作δ.设x∈X，则点x的σ-邻域记作Ux，点x的σ-邻域基记作γx，σx表示包含点x的所有σ-开集(σ-邻域)构成的集族.文中关于拓扑空间的邻域、基、子基、邻域基等概念均见文献[10]，在此不赘述.

定义1[10]设X是一个集合，T是X的子集族.如果T满足如下条件：

1)X，∅∈T;

2)若A，B∈T，则A∩B∈T;

3)若T1⊂T，则∪A∈T1A∈T，则称T是X的一个拓扑.

引理1[10]设X是一个集合，ℬ是集合X的一个子集族(即ℬ ⊂P(X)).如果ℬ满足条件：

1)∪B∈ℬB=X;

2)如果B1，B2∈ℬ，则对于任何x∈B1∩B2，存在B∈ℬ使得

则X的子集族

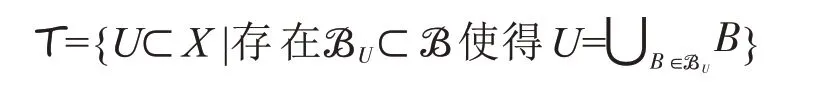
是集合X的唯一的一个以ℬ为基的拓扑.

引理2[15]P(X)的任何子集都是X上的某些拓扑的子基.

定义2[6]设X为非空集合，2X是X的幂集，σ⊂2X，如果对于i∈I≠∅，Ui∈σ，∪i∈IUi∈σ，则称σ为X上的一个σ-结构，称(X，σ)为一个σ-空间.称集族σ中的元素为σ-开集.

定义3[9]设(X，σ)是一个σ-空间，x∈X，如果存在U∈σ使得x∈U，则称U是x的σ-邻域.

定义4[9]设(X，σ)是一个σ-空间，(Y，T)是一个拓扑空间，f：X→Y是一个映射，

1)如果任给V∈T，f−1(V)∈σ，则称f：X→Y是σ-连续映射.

2)如果任给x∈X及Y中包含f(x)的邻域V，存在X中U∈σx，使得f(U)⊂V，则称f在点x处σ-连续.

定义5[9]设(X，σ1)和(Y，σ2)为σ-空间，f：X→Y是映射，

1)若对于任意U∈σ2，f−1(U)∈σ1，则称f：X→Y是(σ1，σ2)-连续映射.

2)若对于任意x∈X，以及Y中包含f(x)的σ-邻域V，存在X中包含x的σ-邻域U，使得f(U)⊂V，则称f在点x处(σ1，σ2)-连续.

定义6[16]设C是U的一个覆盖，K∈C，如果K可以表示成C-{K}中若干元的并，则称K是C的可约元.否则，称K不是可约元.

2 σ-空间的基

本节对比拓扑空间中基的定义方式，同时结合σ-结构的条件定义了σ-空间的基，并且讨论了相关性质.

首先文献[10]给出了拓扑空间中基的定义，且Khayyeri R 和Mohamadian R[11]类比拓扑空间中基的定义方式定义了广义拓扑空间的基，那么可否仿照拓扑空间中基的定义方式定义σ-空间中的基?以下例子说明按照拓扑空间基的定义形式定义σ-空间的基不合理.

例1设X={a，b，c}，δ={{a}，{b}}，σ1={{a}，{b}，{a，b}}，σ2={∅，{a}，{b}，{a，b}}.容易验证，σ1，σ2都是集合X上的一个σ-结构，且δ是σ1，σ2的一个子族.若依据拓扑空间基的定义，对任意U∈σ1，σ2，都存在δ0⊂δ，使得U=∪B∈δ0B.则δ既是σ1的一个基，也是σ2的一个基.即X的子集族δ不能唯一的确定一个σ-结构以它为基.

对比定义1 拓扑结构的条件3)(即若T1⊂T，则∪A∈T1A∈T)与σ-结构的条件(即对于i∈I≠∅，Ui∈σ，则∪i∈IUi∈σ)可知，拓扑结构条件3)限制了∅必须属于T，但是σ-结构的条件并没有限制∅属于σ.即拓扑结构的条件3)比σ-结构的条件强.所以仿照拓扑空间基的形式定义σ-空间的基不合理.此外，不难发现拓扑空间中基的定义形式与定义1中的条件3)类似.受以上启发，类比σ-结构的条件形式给出σ-空间中基的定义.

定义7设(X，σ)是σ-空间，δ是σ的一个子族，若任意U∈σ，存在Bt∈δ，其中t∈T≠∅，使得U=∪t∈TBt，则称δ是σ的基，或称δ是σ-空间X的一个σ-基或基.特别地，σ是其自身的基.

类似于拓扑空间，对于局部情形，σ-空间中也有类似于基的概念.

定义8设(X，σ)是一个σ-空间，x∈X，则点x的所有σ-邻域构成的X的子集族称为点x的σ-邻域系.因为σx表示包含点x的所有σ-开集构成的集族，所以σx为点x在X中的σ-邻域系.

定义9设X是一个σ-空间，x∈X，σx为x的σ-邻域系.σx的子族γx如果满足条件：对于每一个U∈σx，存在V∈γx，使得V⊂U，则称γx是点x的σ-邻域系的一个基，或简称为x的一个σ-邻域基.

以下例子进一步阐明拓扑基与σ-基的区别与联系.

例2设X={a，b，c}，σ={∅，{a}，{b}，{a，b}}，δ1={∅，{a}，{b}}，δ2={{a}，{b}}.容易验证(X，σ)是一个σ-空间，δ1，δ2都是σ的一个子族.依据σ-基的定义，易知δ1是σ-空间X的一个基.由于存在∅∈σ，对于任意Bt∈δ2，其中t∈T≠∅，都不存在∅=∪t∈TBt.故δ2不是σ-空间X的一个基.而若依据拓扑基的定义方式，δ1显然是σ-空间X的一个基.又因为∅∈σ，而空集是任何集合的子集，故存在∅⊂δ2，使得∅=∪B∈∅B，所以依据拓扑基的定义方式δ1，δ2都是σ-空间X的一个基.即σ-基的定义比拓扑基的定义要强.

下面这个定理为判定某一个σ-开集族(即由σ-开集构成的族)是否是给定的σ-结构的一个基提供了一个易于验证的条件.

定理1设δ是σ-空间(X，σ)的一个σ-开集族(即δ⊂σ)，则δ是σ-空间X的一个基当且仅当对于每一个x∈X和x的每一个σ-邻域Ux，存在Vx∈δ，使得x∈Vx⊂Ux.

证明必要性.如果δ是σ-空间X的一个基，则对于每一个x∈X和x的每一个σ-邻域Ux，由定义3知x∈Ux且Ux∈σ.根据基的定义，存在Bt∈δ，其中t∈T≠∅，使得Ux=∪t∈TBt.那么由x∈∪t∈TBt可知，存在Vx=Bt∈δ使得

这证明δ满足定理中的条件.

充分性.设定理中的条件成立.对任意U∈σ及x∈U，由于U是x的一个σ-邻域，故存在Vx∈δ使得x∈Vx⊂U.于是

因此U=∪x∈UVx，从而δ是σ-空间X的一个基.证毕.

由此，利用σ-基可以判定一个集合是否为σ-开集.即U是σ-空间X的σ-开集当且仅当对任意的x∈U，存在V∈δ使得x∈V⊂U.

在拓扑空间中，并不是一个集合的每一个子集族都可以确定一个拓扑以它为基.由于σ-结构比拓扑结构的条件弱，那么在σ-空间中是否一个集合的每一个子集族都可以确定一个σ-结构以它为基?以下定理给出了答案.

定理2设X是一个集合，δ是集合X的一个子集族(即δ⊂2X)，则X的子集族

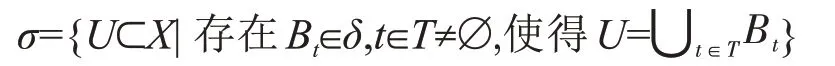
是集合X的唯一一个以δ为基的σ-结构，σ称为由δ生成的σ-结构，δ称为σ的基.

证明对于任意Ai∈σ(i∈I)，则存在Bt∈δ，t∈T≠∅，使得Ai=∪t∈TBt，于是有∪i∈IAi=∪i∈I(∪t∈TBt)=∪t∈∪i∈ITBt∈σ.所以σ是集合X的一个σ-结构，根据σ的定义立即可见δ是σ的一个基.下证唯一性.

假设集合X还有一个以δ为它的一个基.根据基的定义，对于任意存在Bt∈δ，其中t∈T≠∅，使得A=∪t∈TBt，所以A∈σ.这证明另一方面，如果A∈σ，则存在Bt∈δ，t∈T≠∅，使得A=∪t∈TBt.由于，所以又因为A=∪t∈TBt且是一个σ-结构，所以这又证明了综上证毕.

推论1幂集P(X)的任何子集都是X上的某些σ-结构的基.

推论1 与给定的P(X)子集有关，对于P(X)上任何子集都可以构造一个σ-结构，即与子基在拓扑空间中的作用相同.

应用定理2，用先给出基的办法来给定σ-结构.且以下例子说明在σ-空间中X的子集族中是否含有空集，构造出的σ-结构是不同的.而在拓扑空间中，依据基的定义，空集不会影响拓扑结构的生成.从而进一步验证了定义7的合理性.

例3设X={a，b，c}，则有以下结论成立：

1)δ={{a}，{b}，∅}是X的子集族，则σ={∅，{a}，{b}，{a，b}}是集合X的唯一一个以δ为基的σ-结构.

2)δ={{a}，{b}}是X的子集族，则σ={{a}，{b}，{a，b}}是集合X的唯一一个以δ为基的σ-结构.

3)B={{a}，{b}，{a，c}}是X的子集族，容易验证ℬ 满足引理1 的两个条件，则T={{a}，{b}，{a，c}，{a，b}，X，∅}是集合X的唯一一个以ℬ为基的拓扑.

4)B={∅，{a}，{b}，{a，c}}是X的子集族，容易验证ℬ 满足引理1 的两个条件，则T={{a}，{b}，{a，c}，{a，b}X，∅}是集合X的唯一一个以ℬ为基的拓扑.

同样地，利用σ-基可以判定σ-结构的粗细，并获得由不同基生成相同σ的等价条件.

定理3设δ和δ′分别是集合X的σ和σ′的基.下列条件等价：

1)σ′细于σ，即σ⊂σ′;

2)如果B∈δ且x∈B，则存在B′∈δ′使得x∈B′⊂B.

证明1)⇒2).设σ′细于σ，即σ⊂σ′.如果x∈B∈δ，因为δ⊂σ，则B∈σ，于是B∈σ′.由于δ′是σ′的基，故根据定理1，存在B′∈δ′使得x∈B′⊂B.

2)⇒1).设条件2)成立.对任意U∈σ，取x∈U.由于δ是σ的基，所以存在B∈δ使得x∈B⊂U.由条件2)，存在B′∈δ′，使得x∈B′⊂B，于是x∈B′⊂U.又因为δ′是σ′的基，所以U∈σ′，即σ⊂σ′.证毕.

一般来说，基中元素的个数不大于σ-结构中元素的个数，所以用基来刻画连续映射更为简单.以下定理给出讨论.

定理4设(X，σ)是一个σ-空间，(Y，T)是一个拓扑空间，f：X→Y，则f是σ-连续当且仅当拓扑空间Y中有一个基ℬ，使得对于任何一个B∈ℬ，原像f−1(B)是X中的一个σ-开集.

证明必要性.显然，因为Y的拓扑本身便是Y的一个基.

充分性.设ℬ是Y的拓扑的一个基，它满足定理中的要求.如果U是Y的一个开集，则存在ℬ0⊂ℬ使得U=∪ℬ∈ℬ0B，于是

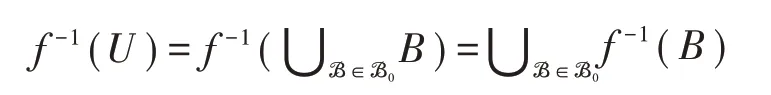
是X中的一族σ-开集之并，所以f−1(U)是X中的一个σ-开集.根据定义4，f是σ-连续.证毕.

定理5设(X，σ1)和(Y，σ2)为σ-空间，f：X→Y，则f是(σ1，σ2)-连续当且仅当σ-空间Y中有一个基δ，使得对于任何一个B∈δ，原像f−1(B)是X中的一个σ-开集.

证明必要性.因为f：X→Y是(σ1，σ2)-连续，σ是其自身的基，所以σ2本身便是Y的一个基.从而σ-空间Y中存在一个基σ2，使得对于任意B∈σ2，原像f−1(B)∈σ1.

充分性.设δ是Y的σ-结构的一个基，它满足定理中的要求.如果U是Y的一个σ-开集，则存在Bt∈δ，t∈T≠∅，使得U=∪t∈TBt，于是

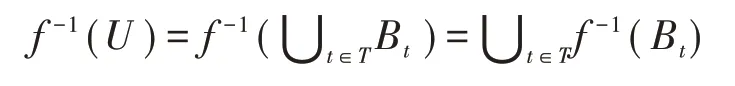
是X中的一族σ-开集之并，所以f−1(U)∈σ1.根据定义5，f是(σ1，σ2)-连续.证毕.

σ-邻域基的概念可以用来验证映射在一点处的连续性.

定理6设(X，σ)是一个σ-空间，(Y，T)是一个拓扑空间，f：X→Y是满射，x∈X.若f(x)有一个邻域基Vf(x)，使得对于任何V∈Vf(x)，原像f−1(V)是x的一个σ-邻域，则f在点x处σ-连续.

证明设Vf(x)是f(x)的一个邻域基，它满足定理中的要求.如果U是f(x)的一个邻域，则存在V∈Vf(x)使得V⊂U.因此f−1(V)⊂f−1(U).因为f−1(V)是x的一个σ-邻域且f是满射，则f−1(V)∈σx，所以f(f−1(V))⊂f(f−1(U))=U.根据定义4，f在点x处σ-连续.证毕.

在拓扑空间中定理6的逆命题成立，那么在σ-空间中其逆命题是否成立?下面的例子给出否定的答案.

例4设X={a，b，c}，Y={b，c}，σ={{b}}，T={∅，{c}，{b}，Y}，则(X，σ)是一个σ-空间，(Y，T)是一个拓扑空间.定义映射f：X→Y满足：f(a)=c，f(b)=c，f(c)=b，容易验证f是满射.由定义4 容易验证映射f在点b处σ-连续.根据拓扑空间邻域基的定义知，对于f(b)=c的任何一个邻域基Vf(b)，都存在V={c}∈Vf(b)，则f−1(V)={a，b}∉σ，故f−1(V)不是点b的一个σ-邻域.逆命题不成立.这与拓扑空间的结论不同，因为σ-邻域的定义比拓扑空间的邻域的定义加强了.

定理7设(X，σ1)和(Y，σ2)为σ-空间，f：X→Y是满射，x∈X.若f(x)有一个σ-邻域基γf(x)，使得对于任意V∈γf(x)，原像f−1(V)是x的一个σ-邻域，则f在点x处(σ1,σ2)-连续.

证明类似定理6的证明即可得证.

以下例子说明定理7的逆命题不成立.

例5设X={a，b，c}，Y={b，c}，σ1={{b}}，σ2={{c}}，则(X，σ1)和(Y，σ2)是σ-空间.定义映射f：X→Y满足：f(a)=c，f(b)=c，f(c)=b，容易验证f是满射.由定义5容易验证映射f在点b处(σ1，σ2)-连续.由σ-邻域基的定义知f(b)=c有且仅有一个σ-邻域基γf(b)={{c}}，故存在V={c}∈γf(b)，则f−1(V)={a，b}∉σ1，所以f−1(V)不是点b的一个σ-邻域.逆命题不成立.

σ-空间中的基与σ-邻域基有以下关联.

定理8设X是一个σ-空间，x∈X，则如果δ是X的一个基，则

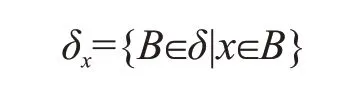
是点x的一个σ-邻域基.

证明可根据定理1直接推得.证毕.

定理9设X是一个集合.则X的子集族δ和是X的同一个σ-结构的两个基的充要条件是δ和满足条件：

1)如果x∈B∈δ，则存在使得

证明必要性.设是X的同一σ-结构的两个基，任意x∈B∈δ，所以B是x的一个σ-邻域.因为是σ的基，由定理1，存在使条件1)成立.同理可证条件2)成立.

设x∈B∈δ，由条件1)存在使从而即任意A∈σ，存在Bt∈δ，t∈T≠∅，使得所以由条件2)类似可证从而故为同一σ-结构的基.证毕.

3 σ-空间的极小基

首先给出σ-空间中并可约元的定义.

定义10设X是一个σ-空间，δ是X上一族非空子集.对于任意的子集B∈δ，若存在δ中的子集族{Bi|i∈I≠∅}使得B∉{Bi|i∈I≠∅}且∪i∈IBi=B，则称B是集族δ的一个并可约元.

接下来看一个简单的例子.

例6设X={a，b，c，d}，σ={∅，{a}，{b}，{a，b}}，容易验证(X，σ)是一个σ-空间.根据σ-空间中基的定义，δ1={∅，{a}，{b}，{a，b}}，δ2={∅，{a}，{b}}都是σ-空间X的基.显然，δ2中元素个数比δ1少，那么在σ-空间中是否存在极小基?即包含元素个数最少的基.

文献[13]给出了一般拓扑空间极小基存在的充要条件，结合例6，这一结论对于σ-空间也成立.

定理10设X是一个集合，δ是X上的一族非空子集，那么δ是X上的某一σ-空间的极小基，当且仅当若δ的一个子集族{Bi|i∈I}满足∪i∈IBi∈δ，则存在i0∈I使得∪i∈IBi=Bi0.

证明必要性.设δ是某一σ-空间的极小基.假设δ的一个子集族δ1={Bi|i∈I}满足∪i∈IBi∈δ，但对于任意子集B∈δ1，∪i∈IBi≠B.那么，存在B′∈δδ1使得∪i∈IBi=B′.这就意味着δ{B′}也是这一σ-空间X的一个基，与δ是极小基矛盾.

充分性.显然，根据推论1 知δ是X上的一族非空子集，则δ是X上的某一σ-空间的基.若δ的一个子集族δ′也是这一σ-空间X的基，则对于任意的子集B∈δ，存在δ′的一个子集族{Bi|i∈I}使得∪i∈IBi=B∈δ，由定理可知，存在i0∈I使得∪i∈IBi=Bi0.故B=Bi0∈δ′，即δ⊂δ′.又因为δ′⊂δ，则δ=δ′.这就证明了δ是这一σ-空间X的极小基.证毕.

结合定理10和定义10得到以下推论.

推论2σ-空间的基δ是极小的当且仅当δ中不存在并可约元.

定义11设(X，σ)是σ-空间，若X只有有限多个元素，则称(X，σ)是一个有限σ-空间.

Stong R E 在文献[14]中指出每个有限拓扑空间都存在唯一的极小基，这是由于有限拓扑空间的每一点都存在唯一的极小开邻域(即包含元素个数最少的开邻域).那么有限σ-空间中的任一点是否存在唯一的极小σ-邻域(即包含元素个数最少的σ-邻域)，有限σ-空间又是否存在唯一的极小基?

例7设X={a，b，c，d}，σ={{a，b，c}，{a}，{b，c}，{a，b}}，则(X，σ)是σ-空间.由σ-邻域的定义知，点b的σ-邻域有{a，b，c}，{b，c}，{a，b}.显然，点b不存在唯一的极小σ-邻域.

那么在有限σ-空间中是否存在唯一的极小基?

定理11设(F，σ)是一个有限σ-空间，则σ-空间F存在唯一的极小基.

证明设Vi(i∈I≠∅)不是σ中的可约元，即Vi不可以表示成σ-{Vi}中若干元的并.设U是所有Vi的集合.因为F是有限σ-空间，所以U是含有有限个元素的集族.根据推论2，容易验证U是σ的一个基，且σ的所有基包含U.故σ-空间F存在唯一的极小基.

4 总结

本文针对σ-空间进行研究，给出了基和极小基的概念，探讨了σ-连续、(σ1，σ2)-连续等性质，以及极小基存在的判定条件.上述结果充分丰富了σ-空间的理论知识，未来将对σ-子空间与σ-积空间的基与极小基和σ-空间的可数性做进一步的研究.