函数图象、性质、求值，分段函数

一、单项选择题

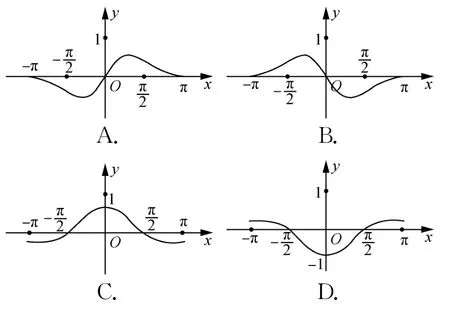
1.（2021·天津高三期末）函数f（x）=在[-π，π]的大致图象是（ ）

2.（2021·泰州高三期末）已知定义在R上的奇函数f（x）满足f（x）=f（x-6），且当0≤x＜3时，f（x）=其中a为常数，则f（2019）+f（2020）+f（2021）的值为（ ）

A.2 B.-2

3.（改编自2020·四川内江高三一模）已知函数f（x）=+sinx+x2021，则f（ln2）+f（ln3）+…+f（ln2020）+（ ）

A.4040 B.2

C.4038 D.9

4.（2020·黑龙江铁人中学高三月考）设函数f′（x）是定义在（0，π）上的函数f（x）的导函数，有f′（x）cosx-f（x）sinx＞0，若a=则a，b，c的大小关系是（ ）

A.a＜b＜cB.b＜c＜a

C.c＜b＜aD.c＜a＜b

5.（2020·重庆八中高三月考）德国数学家莱布尼茨是微积分的创立者之一，他从几何问题出发，引进微积分概念.在研究切线时认识到，求曲线的切线的斜率依赖于纵坐标的差值和横坐标的差值，以及当此差值变成无限小时它们的比值，这也正是导数的几何意义.设f′（x）是函数f（x）的导函数，若f′（x）＞0，且对∀x1，x2∈R，且x1≠x2总有则下列选项正确的是（ ）

A.f（π）＜f（e）＜f（2）

B.f′（2）＜f′（e）＜f′（π）

C.f′（1）＜f（2）-f（1）＜f′（2）

D.f′（2）＜f（2）-f（1）＜f′（1）

二、多项选择题

6.（改编自2020·四川高三模拟）已知函数f（x）=sinx-x，则下列关系正确的是（ ）

A.函数f（x）是奇函数

B.函数f（x）在R上单调递减

C.x=0是函数f（x）的唯一零点

D.函数f（x）是周期函数

7.（改编自2020·上海浦东新区高三一模）已知函数f（x）=则以下说法中不正确的是（ ）

A.f（f））=2

B.f（x）在[0，+∞）上是增函数

C.f（x）是偶函数

D.f（x）的值域为R

三、填空题

8.（改编自2020·山西高三月考）已知函数f（x）=则不等式f（6-x2）＞f（5x）的解集是________.

9.已知f（x）=xlnx-2x+a，x∈[1，e2]，曲线y=f（x）在点（e，f（e））处切线的斜率为________；若存在x0∈[1，e2]，f（x0）≤0，则a的取值范围为________.

四、解答题

10.（2021·石嘴山三中高三期末）已知函数f（x）=x2+alnx.

（1）当a=-2时，求函数f（x）在点（e，f（e））处的切线方程；

（2）若g（x）=f（x）+在[1，+∞）上是单调增函数，求实数a的取值范围.

11.（改编自2020·山东临沂高三期中）已知函数f（x）=-+ax2+bx+ab.

（1）若f（x）是奇函数，求函数f（x）的单调区间；

（2）若f（x）在x=1处有极大值，求当x∈[-1，2]时f（x）的值域.

12.（改编自2020·北京卷）已知函数f（x）=12-x2，设曲线y=f（x）在点（t，f（t））处的切线与坐标轴围成的三角形的面积为S（t），求S（t）的最小值.