松散承压含水层渗透系数变化规律与估算模型研究

陈陆望，彭智宏，王迎新，葛如涛，李蕊瑞

松散承压含水层渗透系数变化规律与估算模型研究

陈陆望，彭智宏，王迎新，葛如涛，李蕊瑞

(合肥工业大学 资源与环境工程学院，安徽 合肥 230009)

我国华北隐伏型煤田的煤系普遍被第四系松散层覆盖，其中的松散承压含水层在煤矿生产中常带来矿井突水、地表沉降、井筒变形破坏等水文地质灾害，造成巨大经济损失和人员伤亡。渗透系数是反映松散承压含水层土体介质渗透能力的重要参数，其数值的合理估算，对该类煤矿水文地质灾害的防治具有重要指导意义。目前，华北隐伏型煤田松散承压含水层渗透系数往往仅通过现场抽水试验确定，基于地质勘探钻孔信息与数据估算松散承压含水层渗透系数的模型研究较少。通过收集淮北煤田祁东煤矿松散承压含水层已有抽水试验的钻孔信息与数据，选取承压含水层厚度、泥层砂层比、最厚砂层占比、有效应力与底砾层厚比作为影响指标，分别与渗透系数进行相关性分析。最终确定底砾层厚比、有效应力、泥层砂层比为关键影响指标，并分析其对渗透系数的影响规律。结果表明，松散承压含水层渗透系数随底砾层厚比的增加而增大，随有效应力和泥层砂层比的增加而减小。在此基础上，采用多元线性回归分析，提出了基于底砾层厚比、有效应力、泥层砂层比的渗透系数估算模型。并将该估算模型应用于淮北煤田祁南、朱仙庄、青东煤矿松散承压含水层的渗透系数估算，结果显示估算结果与试验值一致。

松散承压含水层；渗透系数；底砾层厚比；有效应力；泥层砂层比；多元线性回归

我国华北隐伏型煤田含煤地层普遍被第四系松散层覆盖，该松散层内普遍发育多层以非胶结砂土、砂砾、砾石为骨架的承压含水层，且各含水介质各向异性明显。邻近松散承压含水层的煤层开采，常发生矿井突水、地表沉降、井筒变形破坏等煤矿水文地质灾害，造成巨大经济损失和人员伤亡[1-4]。开展此类煤矿水文地质灾害的防治，很大程度上取决于对该类松散承压含水层渗透系数的合理估算。目前，华北隐伏型煤田松散承压含水层渗透系数往往仅通过现场抽水试验确定，且受人力、物力与财力的限制，能进行抽水试验的钻孔有限，无法反映研究区范围内松散承压含水层现场实际渗透系数的变化规律及其空间效应。已有的研究表明，渗透系数是分析松散含水层各向异性必不可少的参数，若将研究区内整个含水层渗透系数作为常值处理，必然会造成较大误差，因此，开展松散承压含水层渗透系数变化规律的研究具有重要的工程应用价值[5]。

近年来，不少国内外学者对土体渗透系数的变化规律进行了研究。D. W. Taylor[6]指出渗透系数对数值随孔隙比的变化呈线性关系；Jiang Xiaowei等[7]用应力控制孔隙率来解释渗透系数随深度衰减的规律，提出渗透系数与深度的半经验方程；吴婧[8]考虑颗粒级配和密实度对土体孔隙尺寸的影响，提出了基于孔隙尺寸的渗透系数估算模型；张改玲等[9]研究了同一水力梯度下渗透系数随围压大小的变化规律；曾玲玲等[10]提出能反映重塑黏土渗透系数变化规律的数学模型；刘维正等[11]通过固结渗透联合试验，提出适用于天然沉积饱和黏土渗透系数预测模型。但目前已有的估算模型大都是基于室内实验提出，并不适用于计算华北隐伏型煤田松散承压含水层现场实际渗透系数，且该类松散承压含水层介质组成复杂、埋深大，室内实验很难再现其实际的地质与环境。

淮北煤田祁东煤矿在第四系松散承压含水层下开采，煤层顶板突水频发，如3221、3222、7130等工作面在开采过程中均发生了大面积突水。根据矿井水质分析表明，突水水源主要来自松散承压含水层第四含水层(简称四含)。因此，研究四含的渗透性具有重要的工程应用价值。鉴于此，笔者以淮北煤田祁东煤矿四含为研究对象，基于淮北煤田祁东煤矿松散承压含水层大量抽水钻孔信息与数据，采用多元线性回归分析，筛选关键影响指标，分析其对渗透系数的影响规律，建立松散承压含水层渗透系数与关键影响指标的估算模型，并开展该估算模型的验证分析，为松散承压含水层渗透系数的确定提供一种新的科学有效手段。

1 研究区概况与数据获取

1.1 祁东煤矿地质概况

祁东煤矿位于典型的华北隐伏型煤田—淮北煤田宿南矿区境内。淮北煤田地处安徽省北部，华北板块东南缘、郯庐断裂左侧，以宿北断裂为界分为南北2个构造分区。主体构造线有近EW向和NNE向2组，正、逆断层主要为NE和NNE方向，褶皱方向则较多变[12-13]，如图1所示。淮北煤田内煤矿含煤地层普遍被第四系松散层覆盖，研究区祁东煤矿在松散承压含水层下开采过程中曾发生多次突水事故，具有比较典型的研究和参考价值。

祁东煤矿以魏庙断层为界划分为南北2个采区。魏庙断层以北采区松散层厚度为330~450 m，魏庙断层以南采区松散层厚度为360~440 m[13]。

祁东煤矿松散层厚度变化明显，自上而下可划分为4个含水层(组)及3个隔水层(组)，如图2所示。第1含水层(简称一含)为近地表的潜水含水层，2—4层含水层(分别简称二含、三含、四含)为承压含水层[14-15]。其中，四含直接覆盖在煤系之上，是矿井开采的直接充水水源。各含水层岩性多以黏土质砂、粉细砂和中砂为主，垂向上呈交替沉积，一般单层厚度较小，含水层内含有黏土夹层。隔水层多由钙质黏土与砂质黏土组成，第1、第2隔水层厚度较小，普遍小于25 m，隔水性能一般；第3隔水层厚度大，平均厚度达80 m，隔水性能强。

1.2 抽水钻孔数据

现场钻孔抽水试验确定含水层渗透系数是野外水文地质工作中经常采用的较为行之有效的方法之一[16-17]。松散承压含水层的渗透系数通常受到含水层结构、土体粒度、围压大小的影响。初步选取抽水试验钻孔所揭示的承压含水层厚度、泥层砂层比、最厚砂层占比、有效应力与底砾层厚比作为研究对象的影响指标，从中筛选关键影响指标，并探讨其对渗透系数的影响，最后建立相关计算公式。为便于计算，在有效应力计算中，容重统一取15 kN/m3。

此次模型建立选取祁东煤矿部分四含抽水钻孔影响指标数据，见表1。

表1 祁东煤矿部分四含抽水钻孔影响指标数据

2 渗透系数的关键影响指标

为进一步明确表1中各指标对渗透系数的影响程度，对表1中各抽水钻孔指标数据进行相关性分析，分析不同特征指标与渗透系数之间的线性关系显著水平，从而可通过抽水钻孔指标数据建立简单实用的预测渗透系数的表达式。

对表1中数据进行整理，底砾层厚比为0.036~ 0.550，承压含水层厚度为21.31~73.00 m，泥层砂层比为0.042~2.400，最厚砂层占比为0.067~0.548，有效应力为1 527.70~2 428.30 kPa。将上述指标与渗透系数进行Pearson相关性分析，结果见表2，由此可以看出，除底砾层厚比和最厚砂层占比外，其余指标与渗透系数相关性均不高，且仅底砾层厚比、最厚砂层占比、有效应力与渗透系数显著性水平小于0.05，呈显性相关。

表2 各自变量与因变量K相关性

因此，为进一步研究各指标与渗透系数的相关性，对各指标进行对数化处理。选取lg、lg、lg、lg与lg作为自变量，lg作为因变量进行相关性分析，结果见表3。结果显示各自变量与因变量lg的相关性从大到小排序为lg、lg、lg、lg、lg，其中lg与lg间的相关系数过小，且显著性水平大于0.05，线性相关不显著。

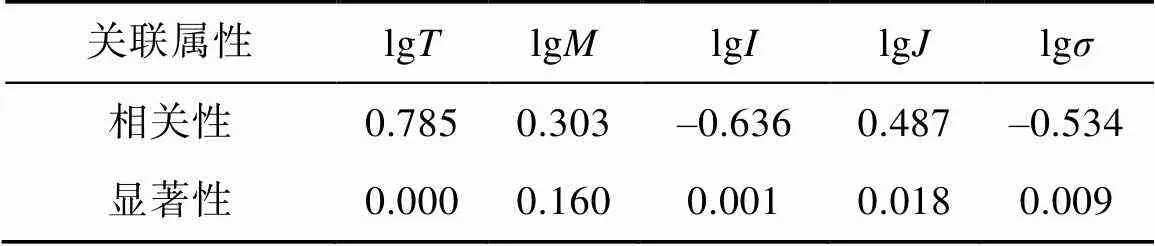
表3 对数化后自变量与因变量lgK的相关性

当一个因变量被多个自变量同时控制时，简单的相关系数通常不能真实地反映因变量与各自变量的关系。因此，为选取适当指标进行回归分析，还需计算各自变量与因变量的偏相关系数[18]。偏相关系数指的是排除其他自变量对某个自变量与因变量的影响后，因变量与该自变量的相关程度，反映自变量与因变量的净相关程度[10]。偏相关系数绝对值越大，说明该自变量与因变量的净相关程度越大。因此，在决定引入哪个自变量进入回归方程时，应以偏相关系数的大小作为判断依据。选定lg作为因变量，、、、、、lg、lg、lg、lg与lg作为自变量，得到不同自变量与因变量的偏相关系数(表4)。

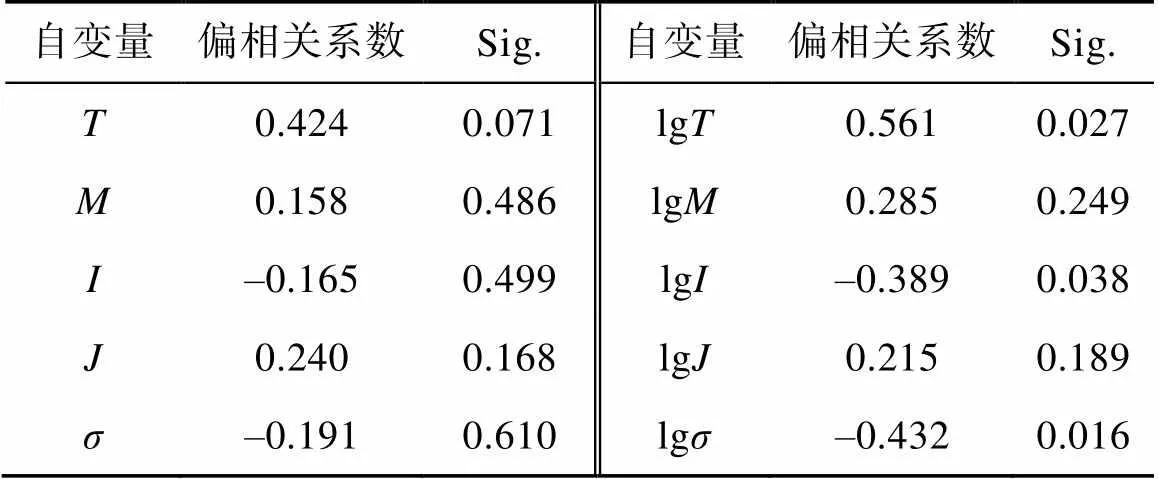
表4 因变量lgK与各自变量偏相关系数统计

结果表明，以lg作为因变量，lg、lg、lg、lg与lg作为自变量的双对数形式的偏相关系数明显高于、、、与作为自变量的半对数形式的偏相关系数。因此，将、、、与剔除出线性回归方程。在对数形式的自变量中，净相关程度从高到低排列为lg、lg、lg、lg、lg。其中，lg与lg的净相关程度最高，lg、lg与lg的净相关程度远低于其他影响指标，且回归系数检验得到的相伴概率值Sig.分别为0.249、0.189，均大于0.05，说明lg、lg与lg之间不仅净相关程度低且线性关系的显著性水平也差，应剔除出回归方程。

综上分析结果，松散承压含水层渗透系数的关键影响指标为有效应力、底砾层厚比和泥层砂层比，且各自变量与因变量之间采取双对数形式所呈现的线性关系最为显著。

3 渗透系数随关键影响指标的变化规律

3.1 底砾层厚比T

淮北煤田四含底部常见含大块砾石的砂土层(底砾层)，受沉积环境影响，底砾层分布无序，其中砾石大小悬殊，对含水层透水性具有显著影响。王祯伟[19]统计了淮北煤田四含碎屑粒度与渗透系数的关系，得出含水层渗透性由粒度结构决定。李江华等[20]对多伦煤矿松散砂砾含水层的底砾层分布情况进行统计，并采用砂土渗溃性试验装置对底砾层渗溃性进行研究。

通过计算底砾层厚度与松散承压含水层厚度的比值(底砾层厚比，计算结果见表1)，可得到底砾层厚比与渗透系数的关系(图3)。

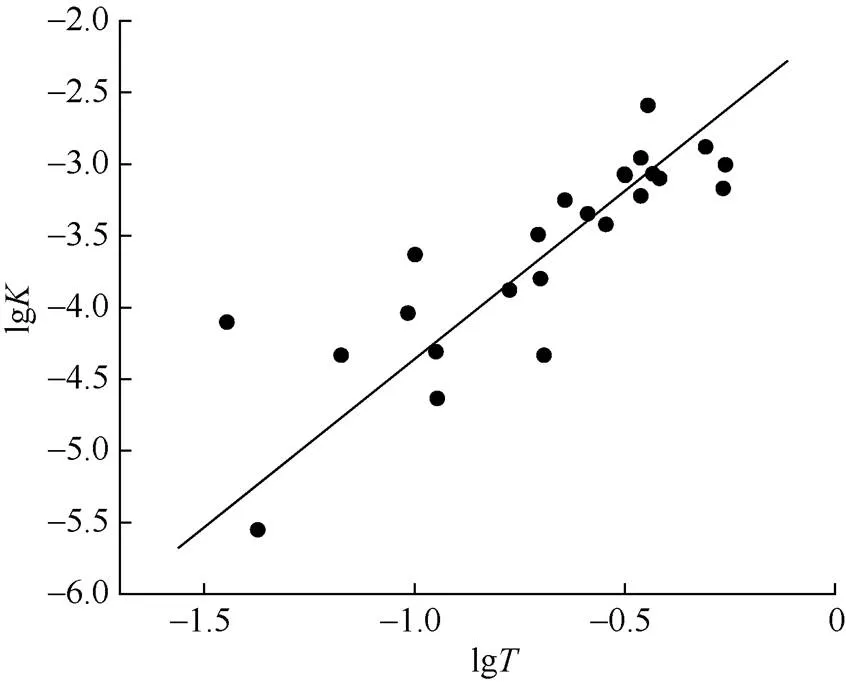
图3 渗透系数K与底砾层厚比T的关系

由图3可以看出，渗透系数随底砾层厚比的增加而增大。

3.2 有效应力σ

从理论上分析，饱和土体中的渗流场与应力场相互作用，相互制约。渗流产生的静水压力和动水压力改变渗透介质的应力状态，渗透介质的透水性也将随应力场的变化而改变。罗晓辉[21]认为，土体渗透系数与有效应力和压缩系数有关；杨志锡等[22]给出了土体渗透系数与有效应力的分段耦合关系式。

整理表1数据，得到松散承压含水层渗透系数随有效应力的变化规律，如图4所示。可见，随着有效应力的增加，渗透系数总体呈下降趋势，这是由于有效应力越大，一些大孔隙越容易受压闭合，颗粒间连通性变差，必然会引起渗透系数的减小[23-27]。

图4 渗透系数K与有效应力σ的关系

3.3 泥层砂层比I

松散承压含水层的组成成分较为复杂，砾石、黏土、砂质亚黏土、含黏土质粉砂、细砂、中砂等交替出现[18]，因此，同一含水层各区域泥层砂层比不尽相同。根据表1中抽水钻孔数据得到松散承压含水层各泥层砂层比与渗透系数的关系(图5)，总体上渗透系数随着泥层砂层比的增加而减小。

图5 渗透系数K与泥层砂层比I的关系

4 模型的建立

为进一步确定松散承压含水层渗透系数的各影响指标与渗透系数间的定量关系，采用多元线性回归方法，得到各关键影响指标与渗透系数的估算模型。根据关键影响指标分析结果，将与渗透系数相关性最高的lg作为主要自变量，分别与lg和lg进行不同组合的多元线性回归分析，以取得最优的估算模型，分析结果见表5。

由表5可知，当模型中lg不作为主要自变量，仅以lg、lg作为自变量的回归方程1相关系数最低。仅以lg作为自变量的多元线性回归方程5，相关系数稍低。分别以lg、lg、lg作为自变量的多元线性回归方程2、方程3与方程4相关系数均在0.79以上。此外，同时考虑lg、lg、lg的多元线性回归方程4相关系数与调整2均高于其他方程，即其线性拟合程度最高。

利用方程4对表1中的渗透系数进行估算，将其结果与抽水试验得到的渗透系数进行对比，如图6所示。图中显示，方程4估算结果与抽水试验结果吻合较好，渗透系数估算值的上下限分别为试验值的3倍和1/3倍，远小于一个数量级，这样的误差范围在渗透系数的估算模型中是可以接受的。因此，松散承压含水层渗透系数估算模型为：

表5 多元线性回归方程、线性系数及显著性特征

注：为相关系数；调整2为可决系数；为方差检验量；Sig.为显著性水平(<0.05)；、、、为数值。

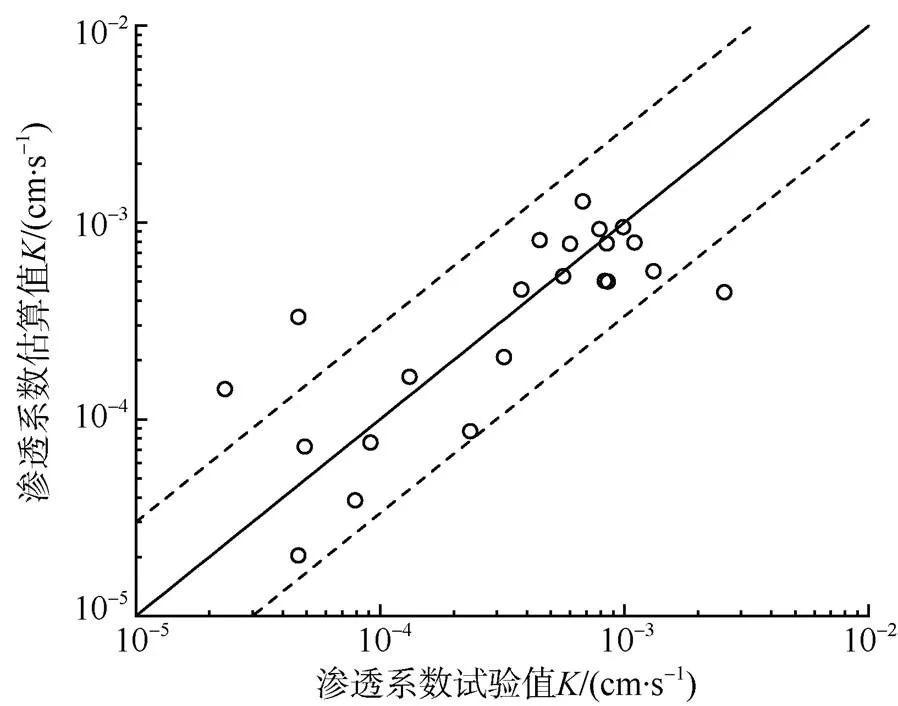
图6 回归模型估算值与抽水试验值对比

lg=0.040+1.186lg–0.964lg–0.468lg(1)

该估算模型说明，当松散层底砾层厚比和有效应力一定时，渗透系数随土体泥层砂层比呈指数递减关系；当底砾层厚比和泥层砂层比一定时，渗透系数随有效应力呈指数递减关系；当有效应力和泥层砂层比一定时，渗透系数随底砾层厚比呈指数递增关系。仅需底砾层厚比、有效应力与泥层砂层比，利用式(1)即可较为准确地估算含水层不同区域的渗透系数，且这些基本拟合参数可通过地质勘探钻孔直接获得，在实际工程中具有重要的应用价值。

5 模型的验证及分析

为验证该模型的正确性与实用性，整理淮北煤田祁南煤矿、朱仙庄煤矿和青东煤矿部分抽水钻孔数据，进行渗透系数估算，结果见表6。

图7是渗透系数估算值与抽水试验值的对比。结果显示，大部分估算值集中于3倍和1/3倍试验值之间，进一步论证了该估算模型的正确性与实用性。

表6 祁南、朱仙庄和青东煤矿部分四含抽水钻孔影响指标数据

续表

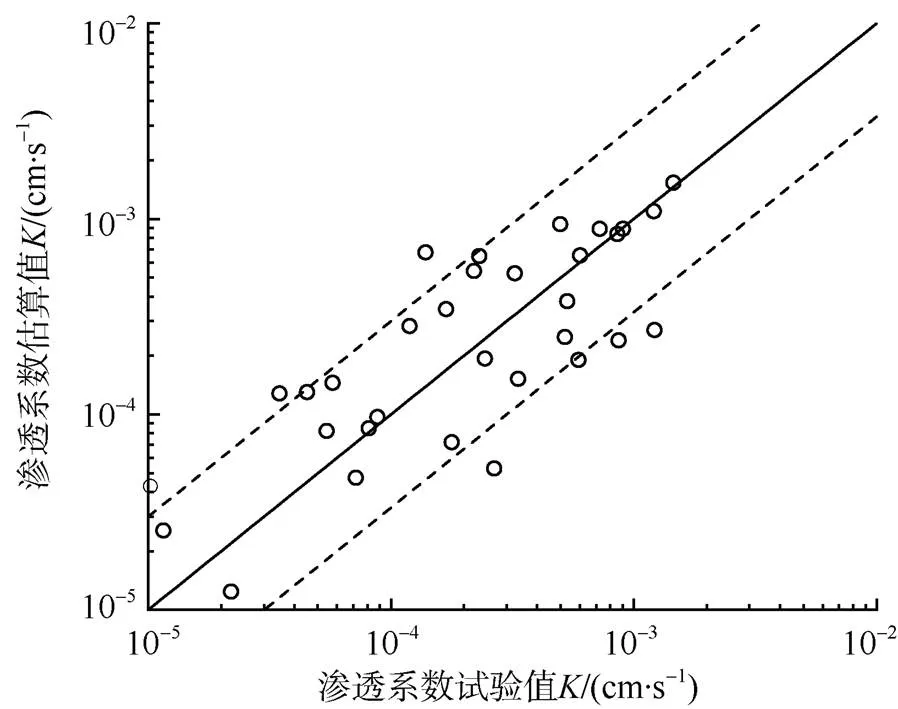
图7 祁南、朱仙庄、青东煤矿渗透系数估算值与抽水试验值对比

6 结论

a.基于祁东煤矿松散承压含水层抽水钻孔资料，通过多元线性回归分析，明确渗透系数的关键影响指标为底砾层厚比、有效应力和泥层砂层比，提出了基于关键影响指标的渗透系数估算模型。

b.渗透系数随底砾层厚比的增加而增大，随有效应力和泥层砂层比的增加而减小，且渗透系数与各影响指标之间所呈现的线性关系以双对数形式最为显著。

c.将所建模型应用于祁南、朱仙庄、青东煤矿，估算其松散承压含水层的渗透系数，结果显示模型估算值与抽水试验值接近，说明模型可应用于含水层大范围渗透系数的确定。

[1] 王晓振. 松散承压含水层下采煤压架突水灾害发生条件及防治研究[D]. 徐州：中国矿业大学，2012. WANG Xiaozhen. Study on occurrence condition and prevention of support crushing and water inrush disaster during mining under unconsolidated confined aquifer[D]. Xuzhou：China University of Mining and Technology，2012.

[2] 许家林，朱卫兵，王晓振. 松散承压含水层下采煤突水机理与防治研究[J]. 采矿与安全工程学报，2011，28(3)：333–339. XU Jialin，ZHU Weibing，WANG Xiaozhen. Study on water-inrush mechanism and prevention during coal mining under unconsolidated confined aquifer[J]. Journal of Mining & Safety Engineering，2011，28(3)：333–339.

[3] 武强，金玉洁，董东林，等. 华北型煤田防治水决策优化管理技术[J]. 煤田地质与勘探，1998，26(4)：41–44. WU Qiang，JIN Yujie，DONG Donglin. Technique of optimizing management of controlling mine water for North China coal field[J]. Coal Geology & Exploration，1998，26(4)：41–44.

[4] 孙亚军，陈歌，徐智敏，等. 我国煤矿区水环境现状及矿井水处理利用研究进展[J]. 煤炭学报，2020，45(1)：304–316. SUN Yajun，CHEN Ge，XU Zhimin，et al. Research progress of water environment，treatment and utilization in coal mining areas of China[J]. Journal of China Coal Society，2020，45(1)：304–316.

[5] 谢新宇，刘育民，潘秋元. 渗透系数变化对一维大变形固结性状的影响[J]. 岩土工程学报，2000，22(4)：509–511. XIE Xinyu，LIU Yumin，PAN Qiuyuan. Effects of variable permeability on one-dimensional large strain consolidation[J]. Chinese Journal of Geotechnical Engineering，2000，22(4)：509–511.

[6] TALOR D W. Fundamentals of soil mechanics[M]. New York：John Wiley & Sons Inc.，1948.

[7] JIANG Xiaowei，WANG Xusheng，WAN Li. Semi-empirical equations for the systematic decrease in permeability with depth in porous and fractured media[J]. Hydrogeology Journal，2010，18(4)：839–850.

[8] 吴婧. 基于孔隙尺寸的粗粒土渗透系数计算方法研究[J]. 人民长江，2017，48(10)：74–78. WU Jing. Permeability coefficient calculation of coarse grain soil based on pore-size distribution technique[J]. Yangtze River，2017，48(10)：74–78.

[9] 张改玲，王雅敬. 高围压下砂土的渗透特性试验研究[J]. 岩土力学，2014，35(10)：2748–2754. ZHANG Gailing，WANG Yajing. Experimental investigation of hydraulic conductivity of sand under high confining pressure[J]. Rock and Soil Mechanics，2014，35(10)：2748–2754.

[10] 曾玲玲，洪振舜，陈福全. 压缩过程中重塑黏土渗透系数的变化规律[J]. 岩土力学，2012，33(5)：1286–1292. ZENG Lingling，HONG Zhenshun，CHEN Fuquan. A law of change in permeability coefficient during compression of remolded clays[J]. Rock and Soil Mechanics，2012，33(5)：1286–1292.

[11] 刘维正，石名磊，缪林昌. 天然沉积饱和黏土渗透系数试验研究与预测模型[J]. 岩土力学，2013，34(9)：2501–2507. LIU Weizheng，SHI Minglei，MIAO Linchang. Experimental study of permeability coefficient of natural saturated clay and its prediction model[J]. Rock and Soil Mechanics，2013，34(9)：2501–2507.

[12] 方婷，解国爱，王博，等. 淮北煤田构造特征和形成机制[J]. 煤田地质与勘探，2017，45(3)：1–6. FANG Tin，XIE Guoai，Wang Bo，et al. The structure features and forming mechanism of Huaibei Coalfield[J]. Coal Geology & Exploration，2017，45(3)：1–6.

[13] 冯晓青. 华北隐伏型煤田松散承压含水层下开采顶板突水预测与防治技术研究[D]. 合肥：合肥工业大学，2016. FENG Xiaoqing. Prediction and prevention of water inrush under the unconsolidated and confined aquifer in concealed coalfields in North China[D]. Hefei：Hefei University of Technology，2016.

[14] 黄雪梅. 祈东矿新生界松散层的工程性质研究[J]. 土工基础，2007，21(1)：21–24. HUANG Xuemei，Study on the engineering properties of Qidong mining area Cenozoic Group[J]. Soil Engineering and Foundation，2007，21(1)：21–24.

[15] 陈陆望，何建东，施小平，等. 松散承压含水层水文地质参数分区及水流场数值模拟[J]. 现代地质，2015，29(4)：967–974. CHEN Luwang，HE Jiandong，SHI Xiaoping，et al. Subarea of hydrogeological parameters and numerical simulation of groundwater flow field in the unconsolidated confined aquifer[J]. Geoscience，2015，29(4)：967–974.

[16] 薛禹群，朱学愚. 地下水动力学[M]. 北京：地质出版社，1979. XUE Yuqun，ZHU Xueyu. Groundwater hydraulics[M]. Beijing：Geological Publishing House，1979.

[17] 杜欣，曾亚武，唐冬云. 基于水下抽水试验的岩体渗透系数研究及应用[J]. 岩石力学与工程学报，2010，29(增刊2)：3542–3548. DU Xin，ZENG Yawu，TANG Dongyun. Research on permeability coefficient of rock mass based on underwater pumping test and its application[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(Sup.2)：3542–3548.

[18] 杜怡韩，黄博，曹兵，等. 物理参数影响粉质黏土渗透系数变化规律[J]. 辽宁工程技术大学学报(自然科学版)，2019，38(2)：148–153. DU Yihan，HUANG Bo，CAO Bing，et alInfluence of physical parameters on variation of permeability coefficient of silty clay[J]. Journal of Liaoning Technical University(Natural Science)，2019，38(2)：148–153.

[19] 王祯伟. 论孔隙含水层的沉积特征与水文地质条件的关联机理[J]. 煤炭学报，1993，18(2)：81–88. WANG Zhenwei. Relationship between depositional characteristics of porous aquifer and hydro-geological conditions[J]. Journal of China Coal Society，1993，18(2)：81–88.

[20] 李江华，李宏杰，黎灵，等. 松散砂砾含水层下特厚煤层分层综放开采可行性研究[J]. 煤炭科学技术，2019，47(5)：88–94. LI Jianghua，LI Hongjie，LI Ling，et al. Feasibility study on slicing fully-mechanized caving mining in extra-thick coal seam under unconsolidated gravel aquifer coarse-grained aquifer[J]. Coal Science and Technology，2019，47(5)：88–94.

[21] 罗晓辉. 深基坑开挖渗流与应力耦合分析[J]. 工程勘察，1996，6：37–41. LUO Xiaohui. Coupling analysis of seepage and stress in deep foundation pit excavation[J]. Geotechnical Investigation & Surveying，1996，6：37–41.

[22] 杨志锡，叶为民，杨林德. 基坑工程中应力场与渗流场直接耦合的有限元法[J]. 勘察科学技术，2001，3：32–36. YANG Zhixi，YE Weimin，YANG Linde. The finite element method of direct coupling between the stress field and the seepage field of foundation pit projects[J]. Site Investigation Science and Technology，2001，3：32–36.

[23] 万力，蒋小伟，王旭升. 含水层的一种普遍规律：渗透系数随深度衰减[J]. 高校地质学报，2010，16(1)：7–12. WAN Li，JIANG Xiaowei，WANG Xusheng. A common regularity of aquifers：The decay in hydraulic conductivity with depth[J]. Geological Journal of China Universities，2010，16(1)：7–12.

[24] 吕卫清，董志良，陈平山，等. 正常固结软土渗透系数与固结应力关系研究[J]. 岩土力学，2009，30(3)：769–773. LYU Weiqing，DONG Zhiliang，CHEN Pingshan，et alResearch on relationship between permeability coefficient and consolidation stress of normal consolidation clay[J]. Rock and Soil Mechanics，2009，30(3)：769–773.

[25] 王皓，乔伟，柴蕊. 采动影响下煤层覆岩渗透性变化规律及垂向分带特征[J]. 煤田地质与勘探，2015，43(3)：51–55. WANG Hao，QIAO Wei，CHAI Rui. Overburden rock permeability variation and vertical zoning characteristics under the influence of coal mining[J]. Coal Geology & Exploration，2015，43(3)：51–55.

[26] 李广信. 关于有效应力原理的几个问题[J]. 岩土工程学报，2011，33(2)：315–320.LI Guangxin. Some problems about principle of effective stress[J]. Chinese Journal of Geotechnical Engineering，2011，33(2)：315–320.

[27] 刘希亮，罗静，朱维申. 深部含水层渗透系数均匀试验研究[J]. 岩石力学与工程学报，2005，24(16)：2989–2993.LIU Xiliang，LUO Jin，ZHU Weishen. Uniform experimental study on permeable coefficient of deep aquifer[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(16)：2989–2993.

Variation law and estimation model of permeability coefficient in unconsolidated confined aquifer

CHEN Luwang, PENG Zhihong, WANG Yingxin, GE Rutao, LI Ruirui

(School of Resources and Environmental Engineering,Hefei University of Technology, Hefei 230009,China)

The coal measure strata in the concealed coalfields in North China are generally covered by the Quaternary loose soils. Many hydrogeological hazards, such as mine water inrush, surface subsidence and wellbore deformation failure, have occurred in mining under unconsolidated confined aquifer, which has caused huge economic losses and casualties. The permeability coefficient is an important parameter that reflects the permeability of soil medium in the unconsolidated confined aquifer. A reasonable estimation of its values has important guiding significance for the prevention and control of such hydrogeological hazards. At present, the permeability coefficient of the unconsolidated confined aquifer in the concealed coalfield in North China is often only determined by the pumping test, and there are few models to estimate the permeability coefficient of unconsolidated confined aquifer based on geological exploration borehole information and data. In the paper, the data of the existing pumping test boreholes in the unconsolidated confined aquifer in the Qidong coalmine of the Huaibei Coalfield was collected and the thickness of confined aquifer, the mud-sand ratio, the thickest sand ratio, the effective stress and the thickness ratio of bottom gravel were selected as influencing indices. The thickness ratio of bottom gravel, the effective stress and the mud-sand ratio were determined as the key influencing indices after analyzing the correlation with the permeability coefficient. Therefore, its influence laws on permeability coefficient are analyzed, and the results show that the permeability coefficient of unconsolidated confined aquifer increases with the thickness ratio of bottom gravel, and decreases with the effective stress and the mud-sand ratio. Then, using multiple linear regression analysis, a permeability coefficient estimation model was proposed based on the thickness ratio of bottom gravel, the effective stress and the mud-sand ratio. The estimation model has been successfully estimated the permeability coefficients of the unconsolidated confined aquifer in Qinan, Zhuxianzhuang and Qingdong coalmines of the Huaibei Coalfield, and the estimated results are consistent with the values of pumping test.

unconsolidated confined aquifer; permeability coefficient; thickness ratio of bottom gravel; effective stress; mud-sand ratio; multiple linear regression

移动阅读

语音讲解

P641；TD741

A

1001-1986(2021)01-0189-09

2020-10-09；

2020-11-28

国家自然科学基金项目(41972256)

陈陆望，1973年生，男，湖北蕲春人，博士，教授，博士生导师，从事煤矿防治水方面的研究. E-mail：luwangchen8888@163.com

陈陆望，彭智宏，王迎新，等. 松散承压含水层渗透系数变化规律与估算模型研究[J]. 煤田地质与勘探，2021，49(1)：189–197.doi: 10.3969/j.issn.1001-1986.2021.01.020

CHEN Luwang，PENG Zhihong，WANG Yingxin，et al. Variation law and estimation model of permeability coefficient in unconsolidated confined aquifer[J]. Coal Geology & Exploration，2021，49(1)：189–197.doi: 10.3969/j.issn.1001- 1986.2021.01.020

(责任编辑 周建军)