一种考虑壁面摩擦作用的发射井引射器设计方法
2021-03-31权辉谢建谢政李良
权辉, 谢建, 谢政, 李良
(1.火箭军工程大学 兵器发射理论与技术军队重点实验室,陕西,西安 710025;2.火箭军工程设计研究院,北京 100111)
井下热发射时,火箭由发射台支撑竖立在发射井中.点火后,火箭发动机喷出的高温高速燃气射流在发射井中形成低压区域,井口场坪上的空气在引射效应的作用下,进入发射井对井下设备设施具有冷却作用,减缓了热环境的冲击,这种现象称为发射井引射效应,是发射井的重要特征[1].所以,发射井的优化设计需要对发射井的引射流场进行深入分析,以期在给定流场压强、速度、温度的情况下获得最大的引射系数[2],最大限度减缓热环境影响.
对于引射器的优化设计,当前仍然以一维近似理论为主要分析设计方法[3-4],如Eames理论[5]、EI-Dessouky理论[6]、祝银海理论[7]、Galanis理论[8].随着计算流体力学的发展,CFD和实验相结合也成为引射器设计的重要方向[9-12].对于发射井流场,王飞等[1]和文献[13-14]中采用CFD方法分析了W型发射井出井过程中引射流场变化情况.由于发射井的巨大尺寸和复杂结构,采用CFD方法优化设计时,如果某一参数变化,则存在反复建模,会消耗大量的计算资源,所以CFD方法并不可取.而一维近似理论由于模型简单,计算快捷,在发射井优化设计时具有一定优势.
文献[15]根据一维引射器理论提出了引射器函数和静压协调函数的概念,分析了理想发射井引射器的工作特性.但是所采用的模型并未考虑壁面摩擦作用,根据其方法得到的工作特性与实际发射井存在一定差距.本文在文献[15]的基础上考虑了混合室壁面的摩擦作用,分析壁面摩擦对发射井引射器工作特性的影响;建立发射井引射器的CFD模型,对混合室出口背压、发动机总压和混合室直径变化时的流场特性进行分析;将CFD的计算结果与引射器函数计算结果进行对比,验证壁面摩擦计算模型的可行性.
1 发射井引射器的准一维模型
1.1 准一维模型的基本假设
本文采用与文献[15]相同的发射井模型,发射井引射原理如图1所示.发动机喷出的燃气射流为工作流体,由引射作用进入发射井内的空气为引射流体.1-1截面为火箭发动机出口截面.2-2截面为虚拟喷管[16]出口截面,假设在此截面上火箭发动机正好处于完全膨胀状态,将此截面作为混合室入口.3-3截面为混合室出口截面,假设在此截面之后引射流体和工作流体完全混合.
本文采用引射器函数方法对壁面摩擦作用进行研究,采用如下假设:
① 工作气流和引射气流在混合室入口满足静压匹配关系,流场只有沿流向的速度分量,两股气流均为比热恒定,比热比恒定的理想气体;
② 不考虑混合室内的具体掺混过程,气流在掺混过程中不发生化学反应,且认为混合室出口已完成掺混,混合气流也为理想气体;
③ 气流为绝热流动.
1.2 理想引射器方程组
理想引射器忽略了壁面摩擦作用.其根据工作气流和引射气流的总温总压、气流物性参数和混合室出口压强来求解混合室入口和出口截面上所有流场参数.
设火箭发动机入口总温为T*、总压为p*、比热比为γp、气体常数为Rp、定压比热容为cpp,井口空气总温为T0、总压为p0、比热比为γs、气体常数为Rs、定压比热容为cps,发动机喉部横截面积为At、引射器横截面积为A3;2-2截面上工作流体的压强为p2(根据静压匹配关系,2-2截面上引射流体的静压与工作流体的静压相等,所以统一设为p2)、温度为Tp2、密度为ρp2、速度为vp2、过流面积为Ap2,2-2截面上引射流体的温度为Ts2、密度为ρs2、速度为vs2、过流面积为As2;3-3截面上的温度为T3、密度为ρ3、速度为v3、比热比为γ3、气体常数为R3、定压比热容为cp3、静压为p3,引射系数为u.此外,在求解过程中出现的关于引射流体的量统一加下标s,关于工作流体的量统一加下标p,如果该量仅限于2-2截面,则再加下标2;求解过程中混合流体仅考虑3-3截面,出现的变量统一加下标3.根据文献[15],可以得到理想引射器方程组
(1)
式中,θ、c、b1均为中间变量.
实际引射器由于壁面存在摩擦作用,并不完全符合引射器方程组,计算所得混合室入口压强较实际引射器偏低.为提高设计准确度,需要根据摩擦作用规律对方程组(1)进行修正.
1.3 考虑壁面摩擦的引射器方程组
沿发射井轴向取厚度为dx的微元如图2所示(图2中虚线框).横截面周长为πD3,微元受到的壁面摩擦作用力可以表示为
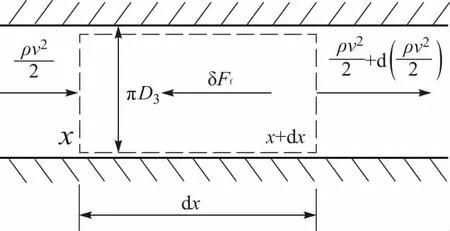
图2 发射井壁面摩擦作用示意图
(2)
式中:cf为微元与壁面之间的摩擦因数;动压ρv2/2为轴向位置坐标x的函数.
考虑到发射井为中心引射,靠近壁面处流体为引射流体,2-2截面与3-3截面之间的发射井壁面受到的摩擦力可以表示为
(3)
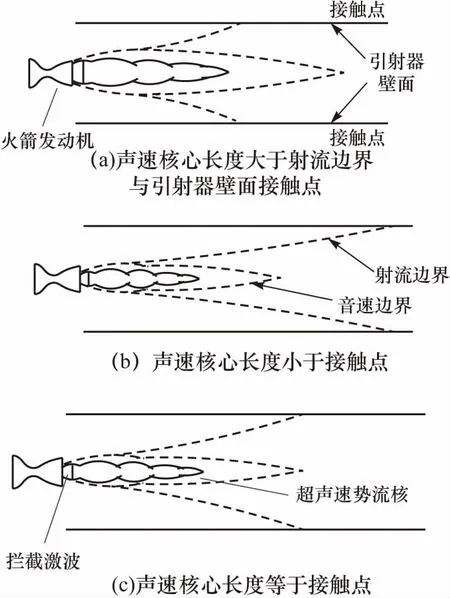
图3 引射器中超声速射流与壁面位置关系示意图
设定混合室入口到接触点之间的轴线长度为Lf1,接触点到混合室出口之间的轴线长度为Lf2,令2-2截面x=0,3-3截面x=Lf,Lf=Lf1+Lf2,式(2)可以化为
(4)
为了进一步简化计算,假设引射流体从2-2截面开始到混合室出口动压呈线性变化,则式(3)可以化为
(5)
混合室前后的动量守恒方程可以写为
mpvp2+msvs2-m3v3=p3A3-p2A3+Ff
(6)
将式(5)和式(6)代入式(1)并替换掉动量方程,可以得到考虑壁面摩擦作用的引射器方程组.
1.4 考虑壁面摩擦的极限引射器方程组
由3-3截面的质量流量表达式、总静温关系式和理想气体状态方程可得
(7)
再将式(7)和式(5)代入动量方程式(6)得
(8)
把式(8)代入式(1),并替换动量方程得到考虑壁面摩擦作用的极限引射器方程组。
考虑壁面摩擦作用的极限引射器方程组在求解过程中,必须满足动量方程的判别式≥0,即
(9)
当Δ=0时,一个p2值仅对应一个v3值,进而对应一个p3值,这形成p2-p3曲线上的驻点条件.结合Δ=0与极限方程组可以形成考虑壁面摩擦作用的驻点极限引射器方程组.
当Δ>0时,一个p2值对应两个v3值,进而对应两个p3值,这时引射器处于不确定状态.可令Δ取最小值,并取两个v3值中的较小者,从而使一个p2值仅对应一个p3值,实现引射器状态的确定.结合Δ的最小值条件与极限方程组并取较小v3值,可以形成考虑壁面摩擦作用的最小极限引射器方程组.
2 考虑壁面摩擦作用的引射器函数和静压协调函数
2.1 引射器函数
2.1.1摩擦引射器函数
把考虑壁面摩擦的引射器方程组中用p2及已知参数表示的未知变量都代入动量方程时,可以得到考虑壁面摩擦作用的基本引射器方程(以下简称摩擦引射器方程).为了便于研究,在此引入摩擦引射器函数Ef(为方便起见,以下简称摩擦引射器函数),摩擦引射器方程可以用摩擦引射器函数表示为
Ef(T*,p*,γp,Rp,T0,p0,γs,Rs,p3,
At,A3,cf,Lf;p2)=
(mpvp2+msvs2-m3v3-Ff)/
(A3+p2-p3)=0
(10)
简记作
Ef(p2)=0
(11)
2.1.2摩擦驻点极限函数
把考虑壁面摩擦的驻点极限方程组中所有已知量、用p2和已知参数表示的未知变量都代入Δ=0式时,得到考虑壁面摩擦作用的驻点极限引射器方程(以下简称摩擦驻点极限方程).同3.1节过程,引入摩擦驻点极限引射器函数EfΔ(以下简称摩擦驻点极限函数),摩擦驻点极限方程可以表示为
EfΔ(T*,p*,γp,Rp,T0,p0,γs,Rs,
At,A3,cf,Lf;p2)=0
(12)
简记作
EfΔ(p2)=0
(13)
2.1.3摩擦最小极限函数
把考虑壁面摩擦的最小极限方程组中所有已知量、用p2和已知参数表示的未知变量都代入Δ并取最小值时,得到考虑壁面摩擦作用的最小极限引射器方程(以下简称摩擦最小极限方程).同3.1节过程,引入摩擦最小极限引射器函数Efm(以下简称摩擦最小极限函数),摩擦最小极限方程可以表示为
Efm(T*,p*,γp,Rp,T0,p0,γs,Rs,
At,A3,cf,Lf;p2)=min(Δ)
(14)
简记作
Efm(p2)=min(Δ)
(15)
2.2 静压协调函数
2.2.1摩擦静压协调函数
理论上,从摩擦引射器方程可以解出用已知量表示p2的函数,称为考虑壁面摩擦作用的基本静压协调函数(以下简称摩擦静压协调函数),用Efp来表示,其表达式记为
p2=Efp(T*,p*,γp,Rp,T0,p0,γs,Rs,p3,
At,A3,cf,Lf)
(16)
简记作
p2=Efp
(17)
2.2.2摩擦最优静压函数
从摩擦驻点极限方程可解出的用已知量表示p2的函数,称为考虑壁面摩擦作用的最优静压协调函数(以下简称摩擦最优静压函数),用Efpo来表示,其表达式记为
p2=Efpo(T*,p*,γp,Rp,T0,p0,γs,Rs,
At,A3,cf,Lf)
(18)
简记作
p2=Efpo
(19)
2.2.3摩擦最小静压函数
从摩擦最小极限方程解出的用已知量表示p2的函数,称为摩擦最小静压协调函数(以下简称摩擦最小静压函数),用Efpm来表示,其表达式记为
p2=
Efpm(T*,p*,γp,Rp,T0,p0,γs,Rs,
At,A3,cf,Lf)
(20)
简记作
p2=Efpm
(21)
3 发射井引射器工作特性
3.1 静压协调函数曲线
当静压协调函数的某个自变量发生变化时,形成函数随该变量变化的曲线,称为静压协调函数曲线.求解具体某个参数的静压协调函数曲线需要用引射器函数作为中间变量,先求取该参数变化时的引射器函数曲线族,再求取曲线族的零点形成静压协调函数的曲线.
静压协调函数共有13个自变量,在发射井的设计中,可以人工控制的重要参数包括发动机的入口参数、发射井尺寸和混合室出口压强.下面分别对p3、p*、D3变化时的静压协调函数展开研究.
当p3变化时,可以求取引射器函数曲线族的零点形成p3的静压协调函数曲线,但是由于引射器有多个零点,所以静压协调函数曲线有多个分支,实际中引射器(如上节算例)并不能形成很低的混合室入口压强,考虑到实际引射器工作状态在参数变化时的连续性和唯一性,静压协调函数曲线取纵坐标最大的分支.以下p*、D3变化时静压协调函数曲线也取纵坐标最大的分支,不再赘述.
取T*=3 000 K,p*=5 MPa,T0=300 K,p0=101 325 Pa,p3=101 325 Pa,发动机喉部直径Dt=0.1 m,发射井直径D3=4 m,Rs=286.890 9 J/(kg·K),γs=1.401 7,Rp=357.562 8 J/(kg·K),γs=1.247 0,p2=0 ~ 101 325 Pa,cf=0.006 5,Lf=30 m为基本取值.
当p3变化其余量不变时,计算得到p3的摩擦静压协调函数曲线如图4所示.
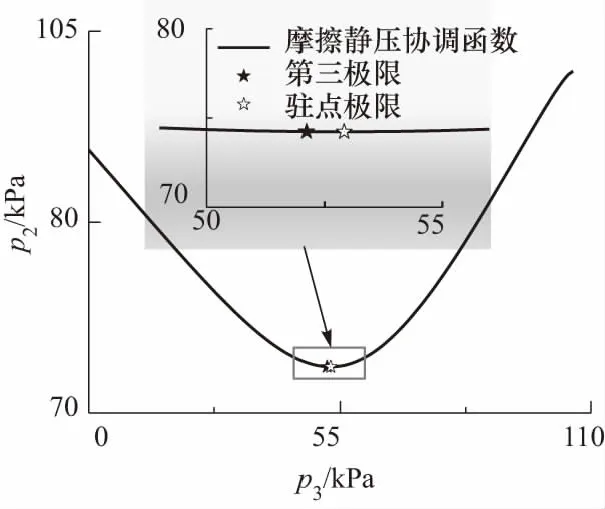
图4 p3变化时的摩擦静压协调函数
当p*变化其余量不变时,计算得到p*的摩擦静压协调函数曲线如图5所示.曲线并不是无限发展,而是从101 325 Pa开始终于约325 MPa.
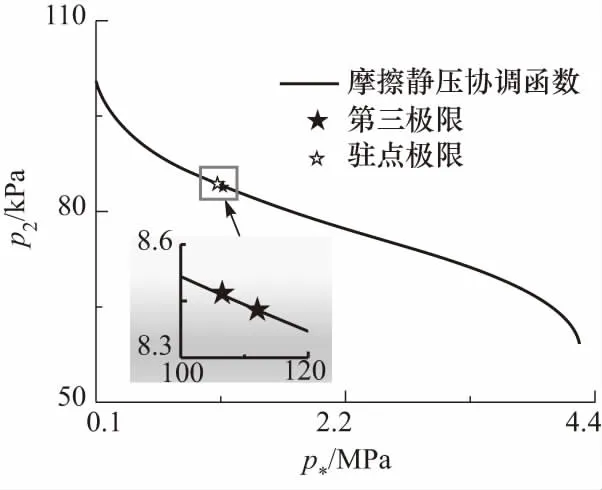
图5 p*变化时的摩擦静压协调函数
当D3变化其余量不变时,计算得到D3的摩擦静压协调函数曲线如图6所示.从图6可以看出,随着D3的增大,p2先是急剧减小而后缓慢增大逐渐趋于水平靠近101 325 Pa.
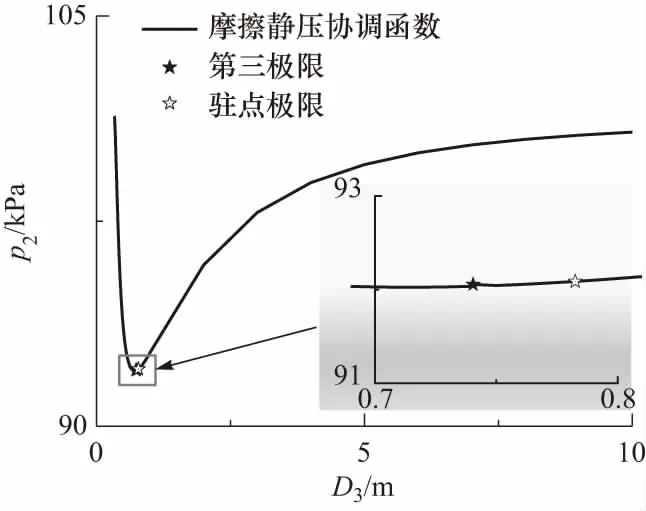
图6 D3变化时的摩擦静压协调函数
3.2 工作特性曲线
采用引射器函数方法时可以使用静压协调函数随着已知参数的变化曲线来反映引射器工作特性[15].考虑壁面摩擦作用的引射器由于极限工作条件的限制,一些设计参数只能在有限范围内取值,这就需要在静压协调函数曲线上做出限制.结合极限工作条件对静压协调函数曲线做出限制和修正的能够反映发射井引射器工作性能的曲线称为发射井引射器的工作特性曲线.本文仅讨论关于p3、p*、D3的工作特性曲线,为方便起见分别记作p2-p3特性曲线、p2-p*特性曲线、p2-D3特性曲线.
3.2.1p2-p3特性曲线
当混合流体达到速度极限时,混合室出口压强不再影响混合室入口参数,p3的降低并不能改变引射器的状态,p2-p3图上工作曲线变为与横轴平行的直线[2].但是文献[2]中研究的是没有考虑混合室壁面摩擦作用的理想引射器,当考虑壁面摩擦作用时情况有所不同,下面进行详细分析.
根据引射器方程组,已知T*、p*、T0、p0、Dt、D3、Rs、γs、Rp、γp、p3、cf、Lf,可以求得唯一确定的p2.如果p2是已知量,则可以根据极限方程组求得两个p3,即唯一的混合室前端状态对应着不唯一确定的后端状态.实际的引射器不可能是随机的二选一状态,所以p2-p3工作状态只能在驻点左右两个单值半边摩擦静压协调函数曲线上.计算可知右半边曲线上混合气流速度均为亚声速,而左半边曲线上混合气流速度存在超声速状态,所以p2-p3工作状态只能位于摩擦静压协调函数右半曲线上.
下面证明第三极限必定位于左半曲线上.由式(8)可得p2-p3图上摩擦静压协调函数取得驻点时速度为
(22)
将驻点条件Δ=0代入式(22)可得
(23)
而混合气流达到声速时速度为
(24)
式中γ3为混合流体的比热比,其可以表示为
(25)
如图4所示,在驻点附近只有p3变化而其余参数不变时,R3、T03变化相对于p3比较缓慢,在驻点极限和第三极限的表达式中可以当成定值.于是当cf、L不为0或者D3不为∞时,
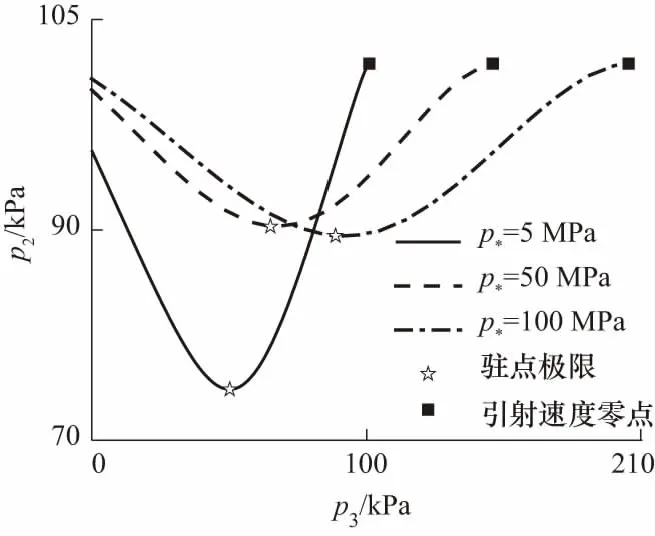
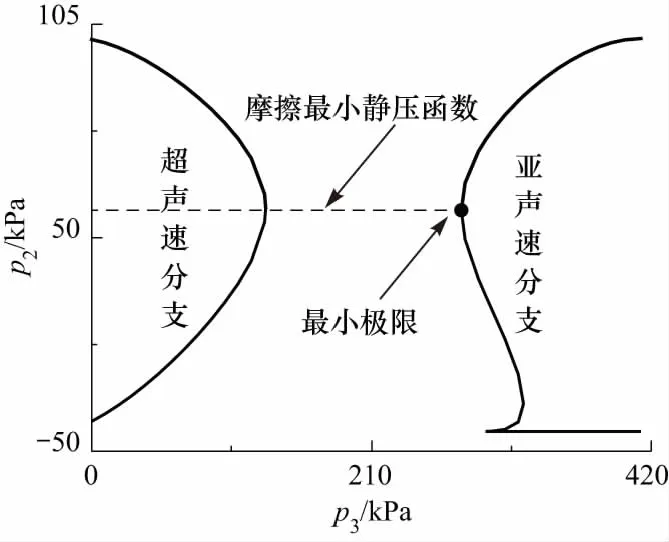
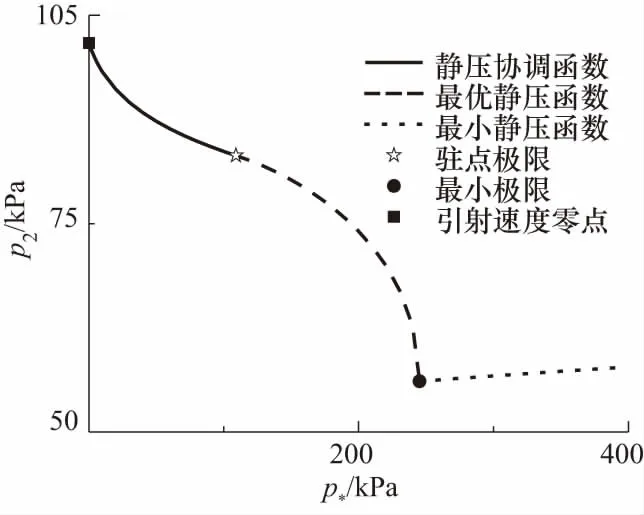
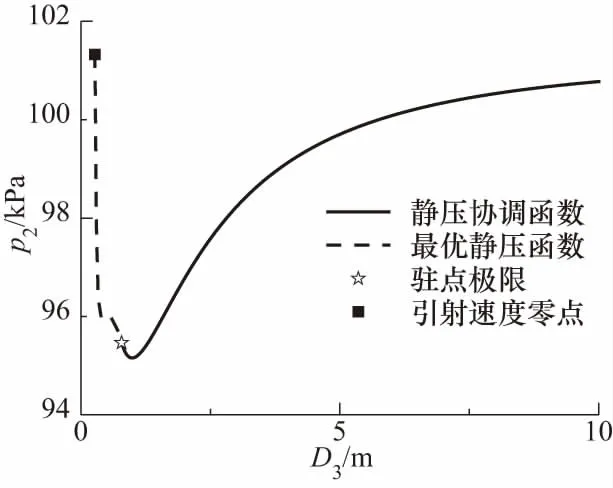
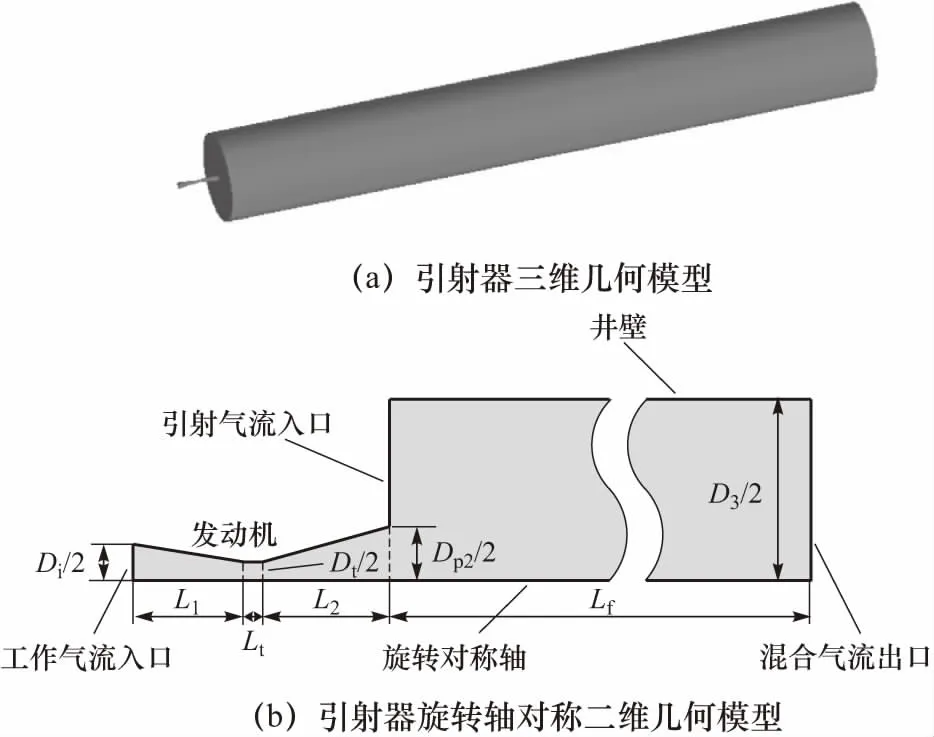
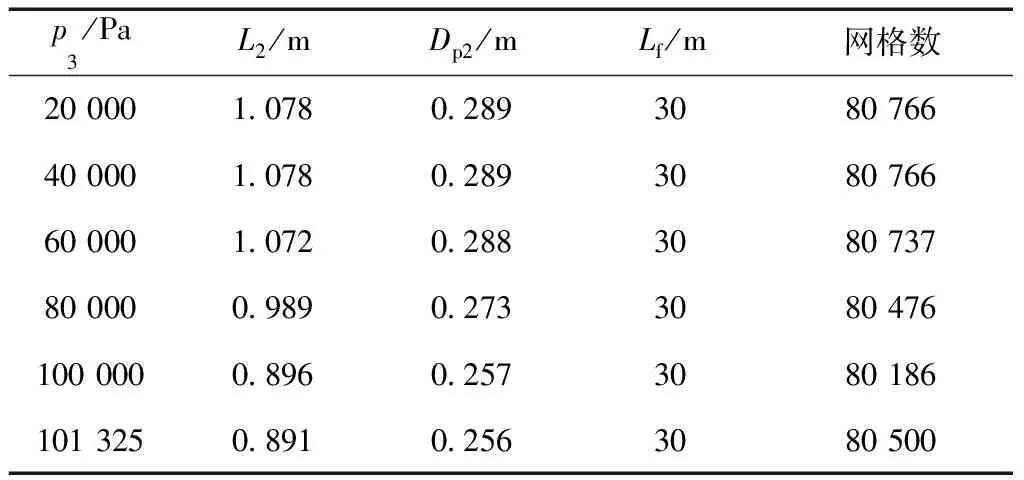
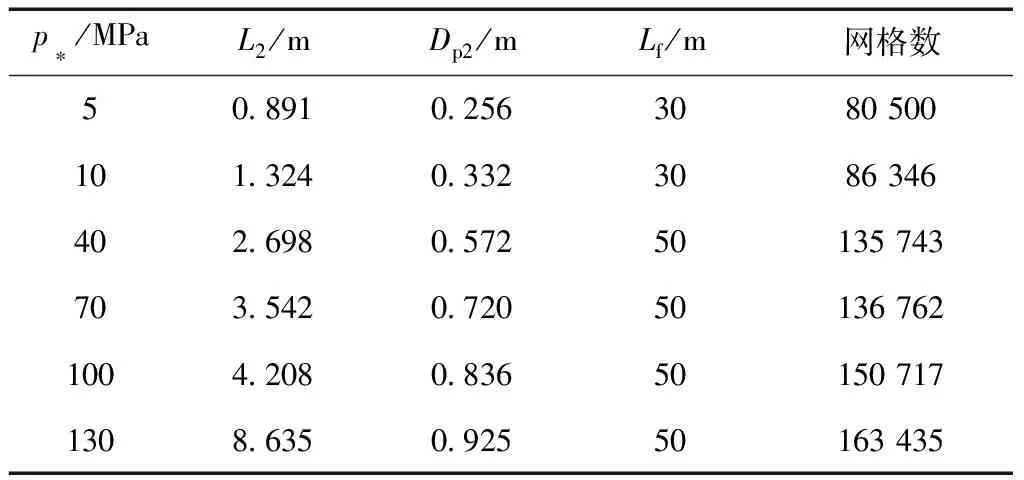
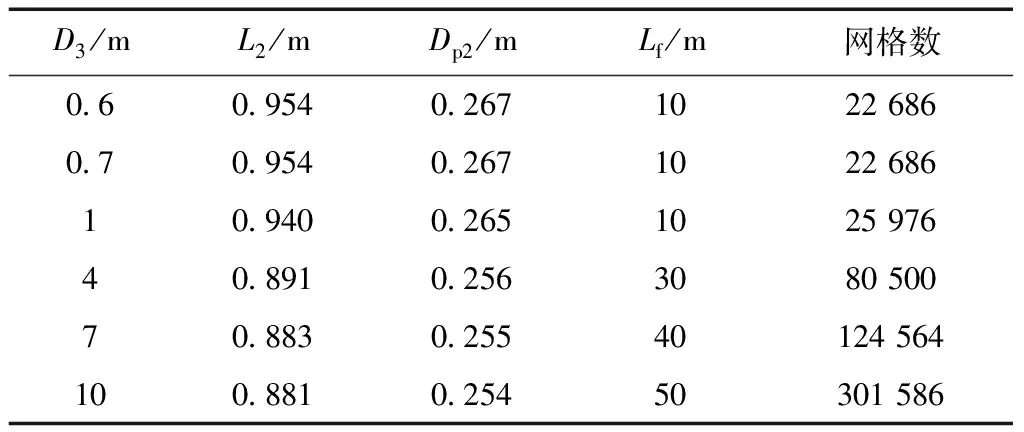
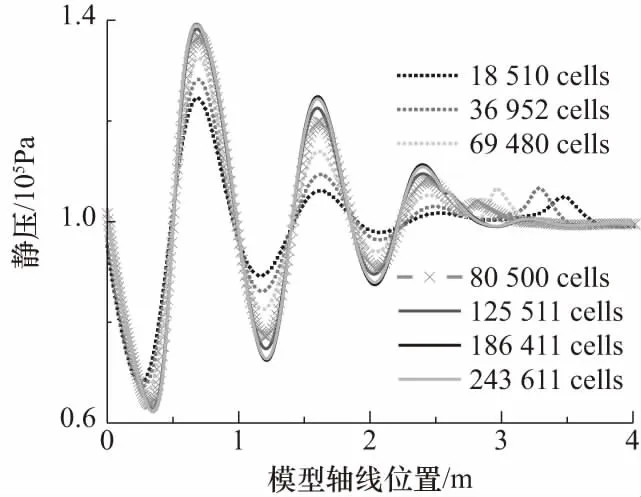
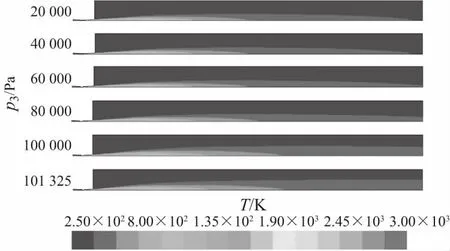
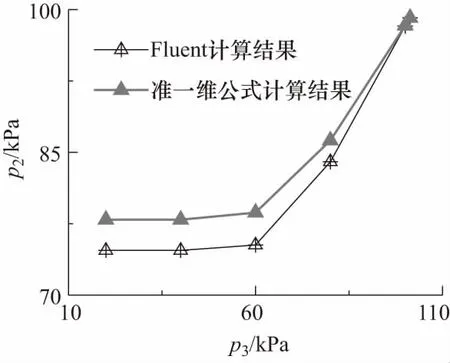
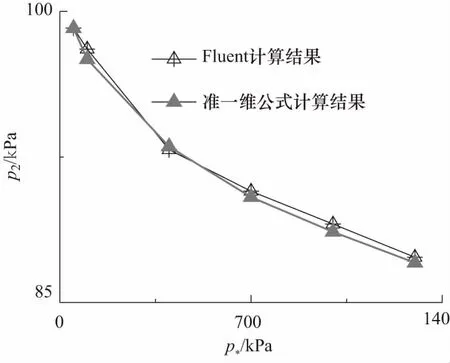
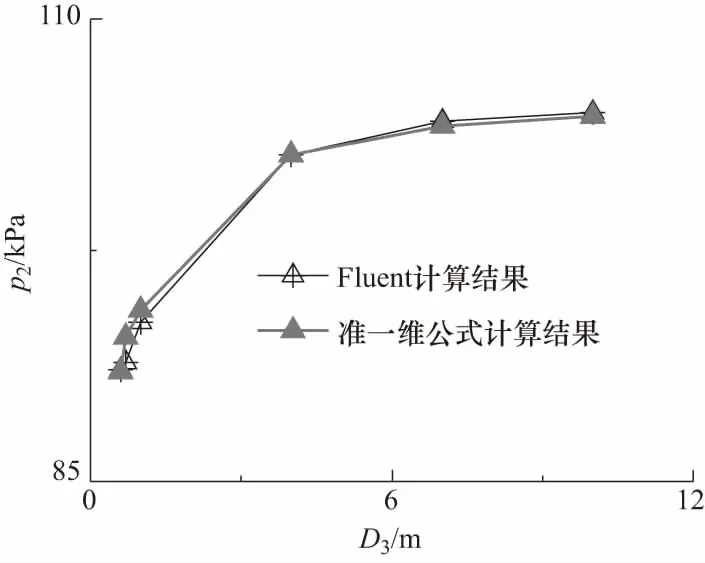
v3Δ (26) 根据(8)式计算可知,在p2-p3图上,摩擦静压协调函数左半曲线上混合气流速度均大于驻点混合气流速度,右半曲线上混合气流速度均小于驻点混合气流速度.所以第三极限必定位于左半曲线上.也即考虑壁面摩擦的发射井引射器在p3变化时不能达到第三极限. 当p3小于驻点极限时,根据前面分析,工作点不能位于摩擦静压协调函数左半曲线,所以必定与p3无关,混合室后端不能影响前端,只能保持驻点状态不变.即随着p3的减小,在p2-p3图上当工作点处于驻点左边时,工作点位于过驻点的与横轴平行的直线段上. 综合以上分析,得到引射器p2-p3特性曲线如图7所示.从图7可以得到,混合室两端的压强都有确定的取值范围,p2为(驻点极限,引射流体总压),p3为(0,引射速度零点),这在发射井设计时必须予以考虑. 图7 p2-p3的工作特性曲线 设计引射器一般考虑的是如何提高引射流体流量.但从图7可以知道,不能通过持续降低混合室出口压强的方法来持续提高引射流量.引流流量有一个最大值,通过降低p3来提高引射流量时,刚达到流量最大值的点具有较高的混合室出口压强,是引射效率最高的点,这个点称为最优点.设计发射井或者单纯的等面积引射器时,应尽量使其处于最优点. 3.2.2p2-p*特性曲线 分别取p*为5,50和100 MPa时得到p3的摩擦静压协调函数曲线如图8所示.从图8可以看出对于每一个给定的p*,对应着一个p3静压协调函数曲线,也就对应一个驻点极限.随着p*增大,对应的p3摩擦静压协调函数曲线向右向上移动,对应的驻点极限(p3Δ,p2Δ)也逐渐向右移动.在p2-p*图上,由于环境p3不变,随着p*增大,存在p3Δ=环境p3点(将这点称为p2-p*图上的驻点极限).在p2-p*图上驻点极限之后,环境p3 图8 不同p*条件下p3的摩擦静压协调函数 当p*继续增大时,摩擦最优静压函数没有零点,式(9)中Δ>0,此时p2-p3图上没有驻点.取p*=300 MPa,p3变化其余参数不变,得到p3的摩擦静压协调函数曲线如图9所示.当p*>246 MPa时,p3的摩擦静压协调函数曲线结构相比于图8发生很大变化,由原来具有驻点的多分支曲线变为没有驻点的亚声速分支和超声速分支.当p3由最大值不断减小时,工作点只能移到亚声速分支上与超声速分支上距离最近的点,此点对应于式(9)取得最小值.工作点不能跳跃进入超声速分支,这是因为实际的引射器物理状态的变化都是连续的,不存在跳跃的情况.工作点也不能沿亚声速分支下移,这是因为,如果工作点下移,则同一个p3值就对应着两个p2值,这是实际引射器物理状态的唯一性相矛盾.将p2-p*曲线上同时满足摩擦最优静压函数和摩擦最小静压函数的工作点定义为p2-p*特性曲线的最小极限点.当p*增大到经过最小极限之后,对应的极限p3cr>环境p3,在p*对应的p2-p3特性曲线上引射器工作在与横轴平行的摩擦最小静压函数曲线段(如图9虚线所示),所以特性曲线必定与环境p3无关,将沿着摩擦最小静压函数曲线发展. 图9 当p* =300 MPa时p3的摩擦静压协调函数 从摩擦最优静压函数和摩擦最小静压函数在最小极限点连续变化来看,引射器不能达到第三极限,只能达到驻点极限.假设混合气流达到声速极限,则工作特性曲线在最小极限点不能连续变化,出现跳跃,与实际物理状态的连续性不相符.这是从另外一个途径证明了考虑壁面摩擦的情况下,引射器只能达到驻点极限,而不能达到声速极限. 随着p*的继续增大,混合室入口静压p2缓慢增大,最终达到p2=p0,引射条件破坏. 综合以上分析,得到引射器p2-p*特性曲线如图10所示.从图可以得到,从引射速度零点开始,混合室入口静压p2随着发动机总压p*的增加而持续降低,在经过驻点极限后降低的趋势逐渐加剧,在经过最小极限点之后,p2随着发动机总压p*的增加逐渐升高,最终趋于p2=p0. 图10 关于p2-p*的工作特性曲线 3.2.3p2-D3特性曲线 当D3变化时,不同D3对应的p2-p3特性曲线也跟随变化,其分析过程与p2-p*特性曲线相同,不再赘述.根据计算分析,得到引射器p2-D3特性曲线如图11所示.随着D3从∞开始减小,p2从p2=p0开始减小,沿着摩擦静压协调函数曲线发展,在降低到一个最小值后有所回升到达驻点极限,而后沿着摩擦最优静压函数发展,p2最终升高到p2=p0.值得注意的是,考虑壁面摩擦作用的情况下,p2-D3特性曲线没有最小极限,但是有一个p2最小值点,这与理想引射器有所不同,在引射器设计时应予以考虑. 图11 关于p2-D3的工作特性曲线 为了验证准一维公式计算发射井引射器的准确性,采用Fluent建模求解并与理论公式的结果进行对照,分析理论公式的适用性,同时也对Fluent模型做出验证. 经过简化后的发射井几何模型如图12(a)所示.为了使CFD模型与引射器函数模型相对应,CFD几何模型中不设专门的引射气流进气道,发动机外壳以外到井壁之间的空间作为进气道.不设扩压段,横截面形状保持圆形不变,管道轴线为直线.考虑到模型的圆柱轴对称特点,在Fluent计算时可以采用旋转轴对称模型,将三维模型转化为二维以简化计算.简化后的旋转轴对称二维几何模型如图12(b)所示. 图12 引射器的几何模型 为了与前文对应,同时尽量避免发动机出口激波带来的总压损失,计算混合室出口压强、发动机总压、混合室直径变化时的发动机出口几何尺寸,使发动机处于微弱欠膨胀状态或者完全膨胀状态得到几何模型各部分尺寸如表1~3所示.其中,发动机亚声速收缩段和喉部采用统一取值,Di为0.264,L1为0.937,Dt为0.100,Lt为0.030.扩张角统一取为10°. 表1 不同p3条件下几何模型参数 表2 不同p*条件下几何模型参数 表3 不同D3条件下几何模型参数 用ICEM划分网格,在发动机位置和几何形状边缘处进行网格加细(网格图不再展示).选用密度基稳态二维轴对称模型,加载能量方程,湍流模式选取Realizablek-ε,组分传输设置两种理想气体分别为空气和自设气体,其中自设气体定压比热容为1 800.136 9 J/(kg·K),摩尔质量为23.251 8 g/mol.发动机入口为压力入口,总、静压取值根据总压和气动函数公式计算得到,总温为3 000 K.引射气流入口为压力出口,压力取值为101 325 Pa,总温为300 K.混合室出口为压力出口,取值根据表1~3变化,总温为300 K.对称轴为axis,其余为wall.选择隐式求解器,二阶迎风格式离散,克朗数设为1. 以D3=4 m的工况进行网格无关性验证.分别取网格数为18 510、36 952、69 480、80 500、125 511、186 411、243 611的6种网格模型计算得到轴线静压如图13所示.从图可以看出,随着网格数的增大,轴线静压曲线逐渐趋于稳定不变,不同网格数轴线静压差距越来越小.网格数为80 500的模型与网格数为125 511、186 411、243 611的3组模型计算结果最大相对误差为3.92%,且其静压与网格数为69 480的模型差距较大.综合比较,选取网格数为80 500的模型网格密度进行所有工况的计算,针对不同几何模型进行适当调整.发动机喷管位置,网格进行适当加密,最小网格尺寸为7.50×10-4m,混合室出口处网格相对稀疏,最大网格尺寸为0.106 m,网格最大长宽比为54.8. 图13 不同网格模型下轴线静压 不同混合室背压条件下温度云图如图14所示,速度云图如图15所示.从图可以看出,总体上,射流温度的扩展范围大于射流速度,出现这种现象的原因是两种流体之间的能量传递除过热对流之外还有热辐射,而动量传递以对流为主要方式.随着混合室出口环境压强的增大,超声速射流的温度边界逐渐扩张,而速度边界逐渐收窄,出现这种现象的原因是随着混合室出口压强的增大,工作流体的动量更多地用于克服逆压梯度,使混合室出口速度减小,轴线或者平均速度的减小使相应的射流速度边界收窄;根据总静温关系,随着平均速度的减小,静温增大,使得相应的温度边界扩张.在p3=20 kPa和p3=40 kPa两种工况混合室中超声速射流边界保持一致,这正是对应于准一维公式中混合室出口环境压强处于驻点极限之下的情况.射流核长度基本不变,可见射流核对混合室出口压强并不敏感. 图14 p3变化时的温度云图 图15 p3变化时的速度云图 不同发动机总压条件下温度云图如图16所示,速度云图如图17所示.从图可以看出,随着发动机总压p*的增大,混合室中超声速射流的温度和速度的扩展范围都逐渐增大;射流核心区的长度明显增长,高温高速区的范围明显增长.这说明射流的动量和能量随着发动机总压的增大均明显增大,对比图14和图15可知,由于混合室出口压强不变,射流温度和速度边界扩展规律没有明显变化;发动机总压对射流核心区的长度具有明显影响. 图16 p*变化时的温度云图 图17 p*变化时的速度云图 不同混合室直径条件下引射器温度云图如图18所示,速度云图如图19所示.从图可以看出,随着混合室直径的增大,射流核长度保持不变,这也说明射流核长度与混合室直径没有关系;在混合室直径较小时,工作流体所占的流通面积较大,混合室管路中存在相当长度的超声速段;在混合室直径较小时,流动形态接近于超声速管道流动,而在直径较大时,流态接近于自由射流. 图18 D3变化时的温度云图 图19 D3变化时的速度云图 由于发动机出口直径计算的过程中没有考虑摩擦作用,按照理想引射器计算,所以发动机出口直径并不完全符合完全膨胀状态,超声速射流存在“葫芦串”,这在发动机总压较高时现象较为明显. 不同混合室出口背压条件下两种方法计算得到的混合室入口压强如图20所示.从图可以看出,随着混合室出口背压的降低,Fluent计算结果和引射器公式计算结果的差距逐渐增大,最大相对误差为4.31%.在p3=20 kPa和p3=40 kPa时,两种方法计算结果曲线均保持水平状态,表明摩擦最优静压函数的提法符合引射器流场规律. 图20 p3变化时Fluent和准一维公式计算得到的p2 不同发动机总压条件下两种方法计算得到的混合室入口压强如图21所示.从图可以看出,随着发动机总压的升高,两种方法计算得到的混合室入口压强均不断降低,而且结果具有很高的一致性.这表明在发动机总压变化时,本文所提引射器函数的一系列公式能够较为准确地描述发射井引射器的流场状态. 图21 p*变化时Fluent和准一维公式计算得到的p2 不同混合室直径条件下两种方法计算得到的混合室入口压强如图22所示.从图可以看出,Fluent计算结果和引射器函数公式计算结果吻合得非常好.这表明在混合室直径变化时,本文所提引射器函数的一系列公式能够较为准确地描述发射井引射器的流场状态. 图22 D3变化时Fluent和准一维公式计算得到的p2 图20~图22两种方法计算结果的比较说明,本文两种计算方法得到了相互映证.实际上本文计算中管道长度根据发动机总压和混合室直径进行了粗略估计,又为了便于结果比较进行了一定取舍选择.壁面摩擦因数根据可压缩流体等截面管道流动理论进行了粗略估计[16],又为了便于比较计算,统一取为了0.006 5.如果对每种工况仔细分析,选择更准确的管道长度和壁面摩擦因数,两种方法计算结果的差距还可进一步缩小. 在发射井引射器的实际设计中应用本文准一维方法,应当充分考虑发射井中发射台等其他设备对壁面摩擦因数的影响,根据实验或者CFD方法获得较为准确的摩擦因数,以期获得较好的设计精度.在实际混合室长度较短时,考虑混合不均匀的影响,实际混合室长度较长时,对引射流体动压沿混合室轴线的分布规律进行调整. 本文根据发射井构型特点提出了采用等面积引射器描述发射井的方法并充分考虑了壁面的摩擦作用,提出了摩擦引射器模型,分析了当p3、p*、D3变化时的引射器工作特性.采用Fluent建模仿真的方法研究了当p3、p*、D3变化时的引射器混合室流动规律,并与引射器公式计算结果进行了对照验证.通过研究得到以下结论: ① 在考虑壁面摩擦作用的情况下,第三极限不能达到,引射器只能达到驻点极限.p2-p3特性曲线在引射速度零点和驻点极限之间均服从摩擦静压协调函数,在混合室出口压强小于驻点极限时是与横轴平行的直线.p2-p*特性曲线在引射速度零点和驻点极限之间均服从摩擦静压协调函数,在驻点极限和最小极限之间服从摩擦最优静压函数,在最小极限之后服从摩擦最小静压函数直至混合室入口压强趋于101 325 Pa.p2-D3特性曲线没有最小极限,在驻点极限和引射速度零点之间服从摩擦最优静压函数,在驻点极限之后服从摩擦静压协调函数. ② 随着混合室出口压强的增大,混合室超声速射流的温度边界逐渐扩张,而速度边界逐渐收窄.随着p*的增大,射流的温度边界和速度边界扩张,射流核增长.在D3变化时,射流核长度基本不变,但是D3越小,超声速段长度越长,引射器混合室内流场越接近于管道流动,D3越大,引射器混合室内流场越接近于自由射流. ③ 按照本文所提的摩擦作用计算方法,在p*、D3变化时,Fluent计算结果和引射器函数方法的一系列公式计算结果吻合得很好.在混合室出口背压p3变化时,随着p3的减小,Fluent计算结果和公式计算结果的差距逐渐加大,但最大误差为4.31%,在驻点极限以下,误差保持不变.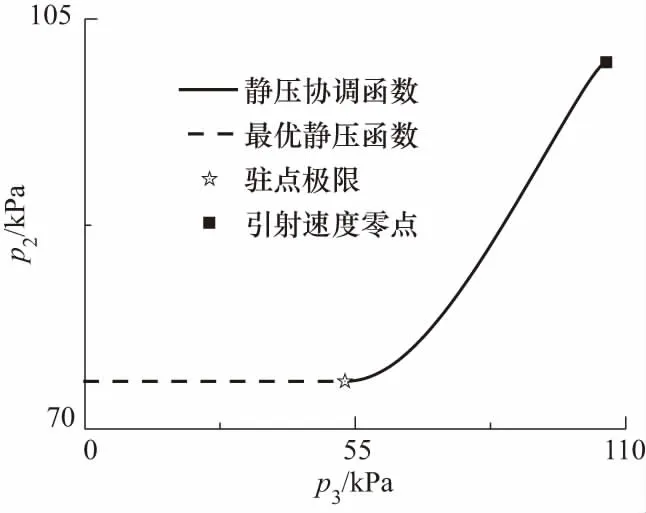
4 Fluent发射井引射器流场分析
4.1 模型构建
4.2 计算结果





5 两种方法的比较
6 结 论
