基于梯度方向的反马赛克算法

仲顺安， 郭宇豪， 马越， 任仕伟， 王卫江

(北京理工大学 信息与电子学院,北京 100081)

现如今镜头广泛应用于数码相机、手机、平板电脑等消费电子产品，电子产品中的彩色数字图像的每个像素通常由3个通道，即红(R)、绿(G)、蓝(B)来描述，理论上来讲得到一幅完整的彩色图像需要3个CMOS感光原件，分别获得红、绿、蓝3个通道的分量.但实际上为了控制产品成本，减少体积，绝大部分电子设备的数码相机都使用一个单一的图像传感器和一个颜色滤波阵列(color filter array, CFA)，在每个像素点记录3个通道中的1个，采集的图像被称作CFA图像或马赛克图像.为了得到一幅完整的彩色图像，需要利用每像素位置1个分量的信息，对另外2个分量进行插值处理，恢复整幅图像的R、G、B分量，这一过程被称作CFA图像插值或反马赛克处理(Demosaicing).

目前使用最广泛的颜色滤波阵列是Bayer格式的CFA[1]，如图1所示.Beyer阵列按照五点形的方式对G分量进行采样，按照矩形的方式对R、B分量采样，每个2×2像素大小的范围中包含2个G分量，1个R分量和1个B分量，本文中只讨论关于这种Bayer阵列CFA图像的反马赛克插值问题.

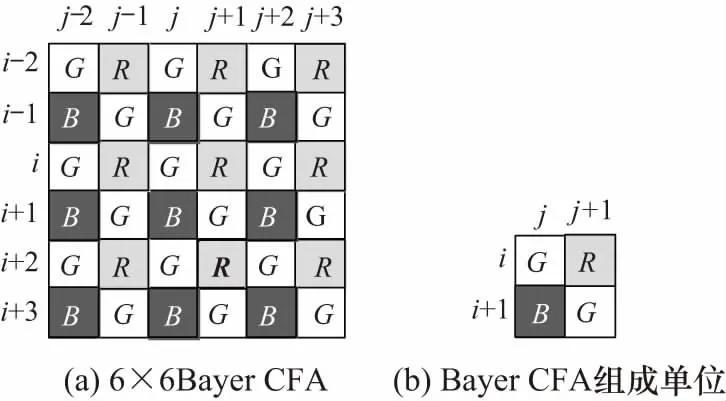
图1 Bayer模式CFA

常见Bayer CFA图像反马赛克算法有标准图像插值法[2]，边缘方向插值法[3]，颜色差分插值法[4]，交替映射插值法[5]等.由邻近插值法，双线性插值法等计算简便的算法组成的标准图像插值法将Bayer图像分成R、G、B三个通道分别进行插值.边缘方向插值法通过分析发现，跨边界方向的插值会导致恢复图像边界模糊，所以提出对于G分量判断边缘方向，并沿边缘方向进行插值，对于R，B分量仍使用原有的双线性插值方法.交替映射插值法利用R、G、B三通道之间很强的相关性，特别是在图像高频区域，经过分解滤波器提取高频和低频分量，通过综合滤波器进行重构，参考G通道的高频分量，经过多次迭代修正R、B通道的高频分量.

在许多实际应用中，反马赛克的处理过程往往包含在数码相机内，或者使用光学传感器的硬件数字系统中，所以一个优质的反马赛克算法需要同时满足满足算法易于实现和算法性能优质两个要点.文献[2-4]提到的反马赛克方法易于硬件实现，但是算法的复合峰值信噪比(composite peak signal noise ratio，CPSNR)较低，文献[5]所提出的算法可以获得较理想的CPSNR，但是多次迭代造成计算量增大、计算过程复杂.上述文献算法基于硬件需要，进行改进后，提出了兼具性能与运算量优势的自适应比例合成反马赛克算法PCA(proportional combination algorithm)[6]和EODM(edge-oriented demosaicking)[7]，并以后者为基础完成相应超大规模集成电路的设计.在充分研究上述算法的基础上，本文提出一种基于梯度方向的反马赛克算法，可以获得比文献[2-4]和文献[6]更高与文献[7]相当的CPSNR性能，运算量远小于文献[5]，易于硬件数字系统实现.

1 算法结构

自然图像的红、绿、蓝3个通道平面之间具有非常高的相关性[8]，梯度变化上有很强的相趋性.因此，本文利用待插值像素点及其周围的梯度变化规律，进行红、绿、蓝3通道的插值运算.如图2，这里提出的反马赛克算法主要有3部分构成，分别是水平和竖直梯度的计算(weighting gradient calculator，WGC)，绿色通道的插值(G-plane interpolator，GI)，红、蓝通道的插值(RI&BI).

图2 算法数据流

通过对Bayer格式的图像进行分析可以发现，一方面，每一个R和B分量的四周都被G分量包围，可以从水平和垂直两个方向对G分量插值恢复，便于结合水平和垂直方向的梯度；另一方面G分量的信息量是R和B的总和，对G分量插值需要计算的位置更少，得到的结果更准确.所以算法先恢复整幅图像的G分量，这样可以得到更为准确的G分量插值结果，并以此为基础恢复R、B分量，高质量的G分量插值有助于提升整幅图像的反马赛克性能[9].

算法在恢复R、B分量时，利用Bayer图像原有的R、B分量信息进行插值，并用上一步恢复的完整G分量信息进行校正处理，在保证运算量变化不大的情况下，大大提升了反马赛克性能.

2 算法描述

2.1 加权水平和垂直梯度的计算

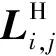
(1)

(2)

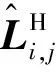
(3)

(4)

(5)

2.2 G分量的插值

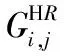
(2Ri,j-Ri,j-2-Ri,j+2)/4

(6)

(2Ri,j-Ri-2,j-Ri+2,j)/4

(7)

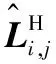
(8)

(9)

(10)

若Pi,j所在位置原本是B像素，那么求这个位置G分量的公式为

(2Bi,j-Bi,j-2-Bi,j+2)/4

(11)

(2Bi,j-Bi-2,j-Bi+2,j)/4

(12)

这样就完成了对整幅图像G分量的插值恢复.接下来将利用G分量的梯度变化对R分量和B分量进行恢复.

2.3 R分量和B分量的插值

以图1的Bayer阵列为例，在Gi,j，Bi+1,j，Gi+1,j+1三处R分量分别取：

Ri,j=(Ri,j-1+Ri,j+1)/2+ΔGHr

(14)

ΔGHr=Gi,j-(Gi,j-1+Gi,j+1)/2

(15)

Ri+1,j=(Ri,j-1+Ri,j+1+Ri+2,j-1+Ri+2,j+1)/

4+ΔGXr

(16)

ΔGXr=Gi+1,j-

(Gi,j-1+Gi,j+1+Gi+2,j-1+Gi+2,j+1)/4

(17)

Ri+1,j+1=(Ri,j+1+Ri+2,j+1)/2+ΔGVr

(18)

ΔGVr=Gi+1,j+1-(Gi,j+1+Gi+2,j+1)/2

(19)

对于B分量的插值，在Gi,j、Ri,j+1、Gi+1,j+1三处，B分量分别取：

Bi,j=(Bi-1,j+Ri+1,j)/2+ΔGVb

(20)

ΔGVb=Gi,j-(Gi-1,j+Gi+1,j)/2

(21)

Bi,j+1=(Bi-1,j+Bi-1,j+2+Bi+1,j+Bi+1,j+2)/

4+ΔGXb

(22)

ΔGXb=Gi,j+1-

(Gi-1,j+Gi-1,j+2+Gi+1,j+Gi+1,j+2)/4

(23)

Bi+1,j+1=(Bi+1,j+Bi+1,j+2)/2+ΔGHb

(24)

ΔGHb=Gi+1,j+1-(Gi+1,j+Gi+1,j+2)/2

(25)

这样就完整恢复了整幅图像的各个颜色分量.

2.4 算法结构对比

图3展示了自适应比例合成反马赛克算法(PCA)与本算法在计算水平梯度时，采用变量选区的区别.在图3(a)所示的PCA计算水平梯度时，将中心的4个像素位置看做一个整体，认为其具有统一的水平梯度，并选取水平邻近的12个Bayer像素值进行计算.而在图3(b)所示的本算法中，将中心4个位置的水平和垂直梯度分开计算，这里以Ri,j+1处为例，只需要考虑其邻近R分量进行计算，提升计算精度的同时减少运算量.

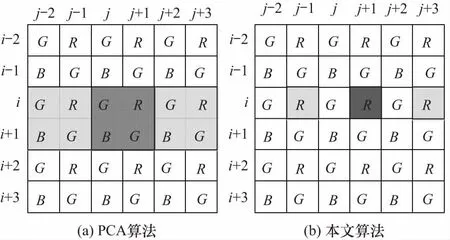
图3 本算法与PCA计算梯度选区的比较

其次，本算法在进行G分量插值时，依据所在位置水平梯度和垂直梯度判断是否存在明显方向性，若处于明显边界处，则按照边界方向进行插值，否则进行比例合成插值，以此提升对G分量插值的精度.而自适应比例合成反马赛克算法(PCA)在进行G分量插值时，直接依据水平梯度和垂直梯度，进行比例合成插值，对于图像中明显边界处的区分不足，容易造成插值误差.

3 各算法处理性能的比较

通常为了衡量一种CFA图像插值算法的性能，有主观和客观两种评价方法.主观上通过观察对比插值图像的视觉效果做判断；客观上通过比较插值恢复图像与原始图像的差异，即计算峰值信噪比(PSNR)或复合峰值信噪比(CPSNR)[10].为了检验本文算法的反马赛克性能，本文采用24幅分辨率为512×768的Kodak set图像[11]作为测试源，将本文提出的算法与目前存在的几种典型CFA图像反马赛克算法的CPSNR性能及运算量进行比较.为了简明起见，本文将双线性插值方法称作方法1，边缘方向插值的方法称作方法2，颜色差分插值算法称作方法3，自适应比例合成反马赛克算法称作方法4，8次迭代的交替映射插值方法称作方法5，本论文提出的改进的基于梯度方向自适应比例合成反马赛克算法称作方法6，EODM算法称作方法7.对比结果如表1和表2所示.

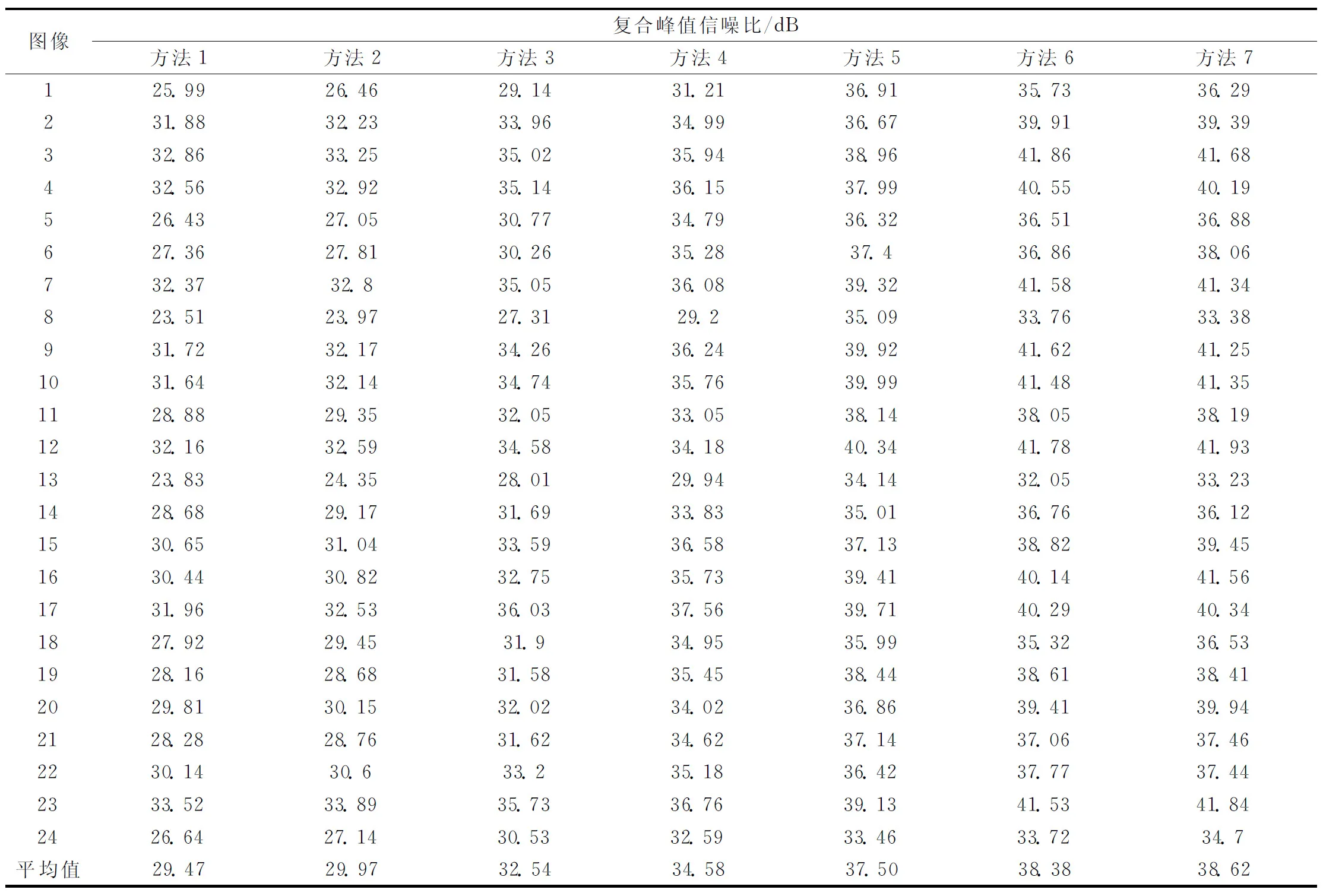
表1 本文提出算法与其他算法的CPSNR性能比较

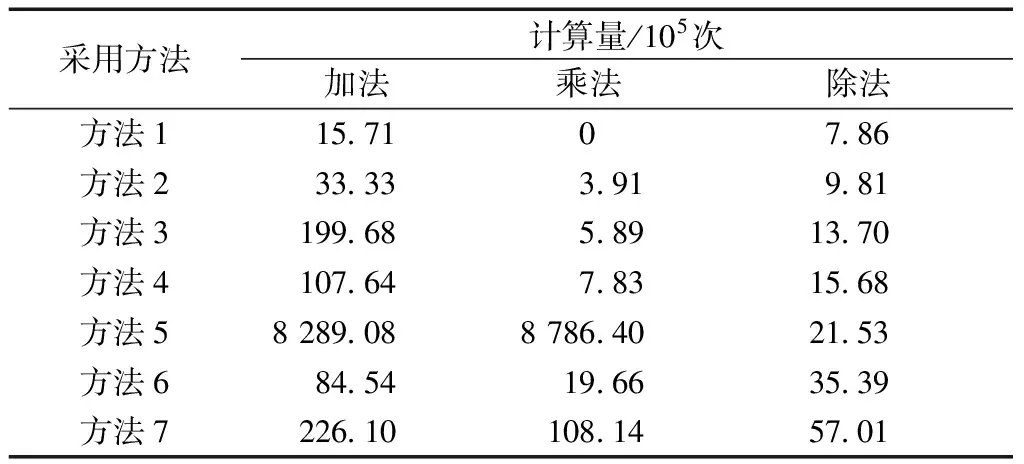
表2 对于512行768列的图像，本算法与其他典型算法运算量比较

按照以下原则对7种方法的运算量进行比较：①图像滤波运算换算成乘加运算;②条件判断分支选择计算量最大的分支进行统计;③矩阵的乘法、求逆运算换算成乘加运算;④不统计像素坐标的计算;⑤不统计绝对值运算.

结合表1、2的数据可以看出：此处提出的方法6，在CPSNR性能上明显优于方法1～方法4，部分优于方法5，与方法7基本相当.在运算量方面，方法6明显小于方法5和方法7，可以说是性价比最优的反马赛克算法.

相比于前几种方法，本算法性能的提升主要是因为，分别计算每个像素位置的水平和竖直梯度，并以此进行方向判断作为G分量插值的依据，大大提升了G分量插值运算的性能，并因此明显优化整体算法性能.

在与近些年提出的EODM算法(方法7)比较中，算法的CPSNR性能基本相当，但是运算量大大降低.这是由于，①本算法直接利用各分量的梯度进行方向判断及插值运算，避免了计算G-R和G-B的值和加权平均的运算；②本算法发现只考虑水平、垂直和没有明显方向3种情况即可以大大优化反马赛克性能，与EODM中的五种情况相比，减少了大量效果改善不显著的运算步骤.

4 结 论

本论文提出了一种基于梯度方向的反马赛克算法，在与其他典型算法CPSNR性能和算法计算量两方面的比较中，均处于优势位置.尤其是在与已经应用到硬件系统的PCA算法的比较中，在运算量基本相当的情况下，大大改善了反马赛克处理后的图像质量；在与VLSI(very-large-scale integration)实现的EODM算法的比较中，两者反马赛克的性能相差不大，但是本算法大大简化了算法步骤，在后续的硬件实现中将节省更多的资源，具有更高的性能代价比.

在数码消费产品日益小型化，硬件资源日益紧张的今天，成像质量高、运算结构简单的本算法更适用于产品的数字图像采集功能.未来可以继续对于本算法提升处理能力的研究，并完成基于FPGA或数字IC的实现，提升其实时处理图像的性能，有机会将其应用在高速摄像机或可穿戴设备当中.