在一题多解中培养思维的灵活性

江苏省泰州实验学校 高明月

思维品质是人的思维的个性特征。思维品质反映了每个个体智力或思维水平的差异，主要包括深刻性、灵活性、独创性、批判性、敏捷性和系统性六个方面。思维的灵活性是建立在思维的系统性和深刻性的基础上，并为思维的敏捷性、独创性和批判性提供保证。因此，培养思维的灵活性显得尤为重要。

一题多解是指从不同的角度，运用不同的思维方式来解答同一道题的思考方法。一题多解是小学数学教学中常用的方法，被认为是提高学生解题能力、培养学生思维灵活性的有效方法。经常进行一题多解的训练，可以锻炼学生的思维，使学生的头脑更灵活。

下面结合两个案例谈谈如何在一题多解中培养学生思维的灵活性。

一、分数除法应用题

问题1：行驶1 千米用汽油多少升？

问题2：1 升汽油可以行驶多少千米？

这道分数除法应用题是苏教版六年级上册“分数除法”单元的习题，学生的困惑是弄不清谁除以谁，经常把被除数和除数写反了。针对这一情况，一题多解的训练不仅可以拓宽学生的解题思路，沟通知识间的内在联系，而且能有效地帮助学生突破难点，培养学生思维的灵活性。

方法一：画图法

借助图形化抽象为具体，弄清数量之间的关系，促进数学理解。

问题1：行驶1 千米用汽油多少升？

（1）画图。把题目中的条件和问题整理在线段图上，如图1：

图1

（3）出示数量关系式：总数÷份数=每份数。

问题2：1 升汽油可以行驶多少千米？

（1）画图。把第一个问题的答案作为已知条件整理在线段图上，如图2：

图2

（3）出示数量关系式：总数÷每份数=份数。

方法二：倍比法

解应用题时，先求出题中两个对应的同类数量的倍数，再通过倍数去求未知数，这种解题的方法称为倍比法。

问题1：行驶1 千米用汽油多少升？

（1）先把条件和问题整理一下。

1 千米 ——？升

问题2：1 升汽油可以行驶多少千米？

（1）整理一下条件和问题：

？千米 —— 1 升

方法三：迁移法

把整数除法的意义迁移到分数除法中来。

把题目中的分数换成整数，就成了这样一道题：“一辆小汽车行驶1000 千米用汽油80 升。问题1：行驶1 千米用汽油多少升？问题2：1 升汽油可以行驶多少千米？”

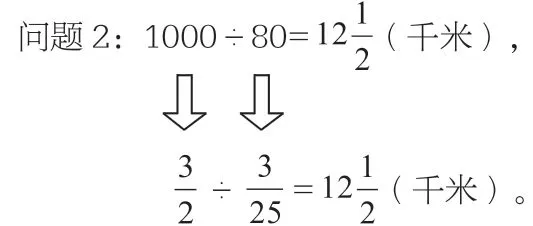
画图法借助直观的图形，有助于弄清数量之间的关系。倍比法把两个同类量进行倍比，可以将纷繁的关系变得简洁明了。迁移法将新知转化为旧知，借助已有的知识经验来解决新问题。通过一题多解的训练，学生能从不同的角度，运用不同的思维方式来思考问题，在思维过程中能从一种解题途径转向另一种解题途径，能举一反三、触类旁通，从而培养学生思维的灵活性。

二、移多补少应用题

【例2】小明和小红各有一些糖，小明给小红3 颗糖以后，小明还比小红多2 颗糖，原来小明比小红多多少颗糖？

这道移多补少应用题是一年级的数学思维训练题。在课前的调查中，多数学生认为原来小明比小红多5 颗糖，错误率较高。一年级学生抽象思维的水平较低，画图法变抽象为具体，再结合详细的讲解，会促进学生的理解。

方法一：画图法和倒推法的融合

（1）指导画图。

从后来的情况想起。后来，“小明比小红多2 颗糖”，他们两人一样多的糖有多少呢？我们不知道，也不需要知道，用省略号表示小明有这么多糖，小红也有这么多糖，这是他们两人一样多的部分，如图3：

图3

“小明给了小红 3 颗糖以后，小明还比小红多2 颗糖”，说明这3 颗糖小明也有。小红的3 颗糖是小明给她的，要还给小明，原来小明比小红多8 颗糖。3+2+3=8（颗）。（如图4）

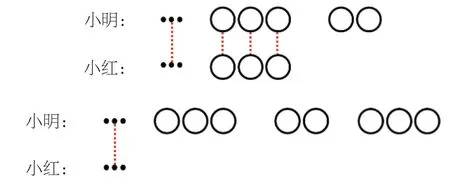
图4

（2）了解“倒推法”。

后来，“小明比小红多2 颗糖”，原来，小明比小红多8 颗糖。由后来的情况去推想原来的情况，这种方法叫作“倒推法”。（如图5）

图5

方法二：画图法、假设法和倒推法的融合

（1）从后来的情况想起，假设小红后来有5 颗糖，那么小明后来有7 颗糖，小红的3 颗糖是小明给她的，要还给小明，原来小明有10 颗糖，小红有2 颗糖，原来小明比小红多8 颗糖。5-3=2（颗）， 7+3=10（颗），10-2=8（颗）。

（2）课件演示。（如图6）

图6

（3）追问：“能不能假设小红后来有2 颗糖呢？”（小明给了小红3 颗糖，小红要还给小明3 颗糖，如果假设小红有2 颗糖，不够还给小明）看来，假设的糖的颗数要够还给别人才行。

在解决问题时，引导学生从后来的情况想起，找到解决问题的突破口，接着指导画图、课件演示，既降低了学生思考的负荷，又让学生体会到倒推法的巨大作用。假设法是先假想出一种结果，再推想出原来两人相差的糖的颗数。

倒推法与假设法的有机融合，使学生体会到解决问题策略的多样性，又培养了思维的灵活性。思维的灵活性体现在：思维起点灵活，从不同角度、方向，用多种方法来解决问题；思维过程灵活，从分析到综合，从综合到分析，全面而深刻地思考问题。多种策略的呈现打开了学生的思路，培养学生从不同角度思考问题的习惯，进而较全面地分析问题、解决问题，再用同类问题加以巩固练习，学生在方法的迁移中，逐步达到举一反三、运用自如的程度，从而提升思维的品质。

学生思维品质的提升是一个漫长的过程，不是一朝一夕就能实现的，只有用心栽培，方能静待花开。