基于人工鱼群算法的两轮机器人运动控制研究
2021-03-29谭志银
谭志银


摘要:为了降低机器人实际运动位置与目标位置跟踪误差,设计了径向基函数(Radial Basis Function, RBF)神经网络控制器。利用人工鱼群算法迭代搜索最优值原理对RBF神经网络控制器进行优化,将优化后的控制器用于两轮机器人控制系统中,并给出了两轮机器人误差控制方程式。同时采用MATLAB软件对两轮机器人的控制系统进行仿真,对比分析优化前和优化后输出误差变化范围。结果表明:优化后两轮机器人在向目标位置移动时产生的误差变化幅度范围较小。利用人工鱼群算法优化RBF神经网络控制器,能够提高控制器的反应速度,降低两轮机器人跟踪目标产生的误差。
关键词:两轮机器人;RBF神经网络控制器;人工鱼群算法;优化;仿真
中图分类号:TH112 文献标志码:A 文章编号:1008-4657(2021)03-0074-05
引言
随着智能化时代的到来,各式各样的机器人也随之而来。其中,仿人机器人研究较多,主要包括双足行走式和轮式两种方式。目前常见的轮式机器人有两轮、三轮和四轮式。轮子越多,行驶相对更加穩定,但是约束过多,结构也相对复杂。两轮机器人具有结构简单、运动灵活,可以在空间较小的范围内执行复杂任务[ 1-2 ]。面对外界各种不确定因素,两轮机器人移动过程中,其控制精度格外重要。因此,必须加快我国机器人控制领域的研究,更好的适应各种复杂环境。
两轮机器人控制系统一直是研究的热点问题,为了使机器人更好的为社会服务,对机器人控制系统展开了研究。文献[ 3-4 ]研究两轮平衡机器人PID控制系统,分析了两轮机器人斜坡简图,构造机器人动力学方程式。设计PID控制系统,通过仿真验证控制系统的稳定性,提高了机器人运动的稳定性。文献[ 5-6 ]研究了两轮机器人神经网络补偿控制系统,设计了两轮机器人结构示意图,引用了BP神经网络控制系统,利用神经网络算法逼近方法提高机器人运动精度,在不同工况条件下对机器人补偿效果进行仿真验证,提高了机器人检测精度。文献[ 7 ]研究了两轮机器人模糊PID控制系统,给出了模糊理论控制算法,引用PID控制系统,给出了模糊自适应PID控制流程,通过仿真对两轮机器人进行验证,证明了控制系统的有效性。以前研究的机器人控制系统,从在某种程度上说,提高了机器人运动轨迹跟踪精度。但是,随着智能化产业的发展,对机器人位置精度的要求也变得越来越苛刻,需要不断的追求高精度控制系统。对此,本文创建了两轮机器人二维模型简图,定义了机器人在向目标位置移动产生的误差方程式,给出了机器人运动路径最短表达式。同时设计了两轮机器人RBF神经网络控制器,利用人工鱼群算法迭代搜索全局最优值原理对控制器进行优化。通过仿真曲线比较优化前和优化后的误差变化范围,为两轮机器人控制系的研究提供参考。
1 两轮机器人
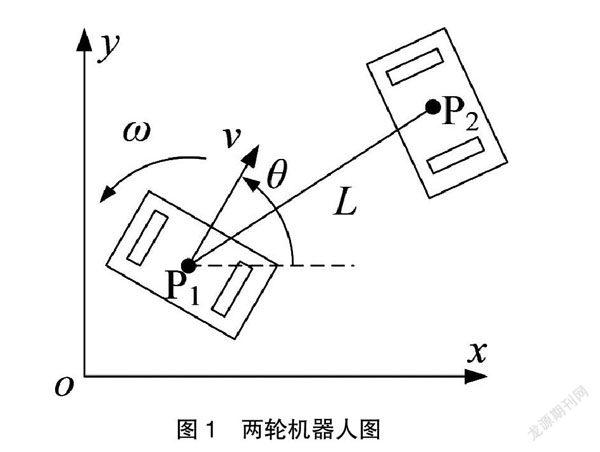
在直角坐标系中,建立两轮机器人运动简图,如图1所示。
在图1,O-xy为直角坐标系,机器人起点位置为P1点,终点位置为P2点,机器人移动位移为L。机器人通过调整自转角度θ和移动速度v从起点位置向终点位置移动。
两轮机器人向目标移动过程中,其速度和角速度[ 8 ]定义为
式中:x、y分别为坐标系横向、纵向位置;ω为两轮机器人自转角速度。
两轮机器人向目标方向运动时,其运动位移误差定义为
式中:s为期望运动位移;sd为实际运动位移。
若要降低两轮机器人运动位移误差,必须使机器人运动路径最短,其表达式为
式中:(xi,yi)为起点位置;(xj,yj)为终点位置。
2 改进RBF神经网络控制
2.1 人工鱼群算法
采用人工鱼群算法,其人工鱼个体位置[ 9-10 ]为
式中:Xi为个体寻优变量。
在人工鱼所在位置处,其食物浓度定义为
式中:f(X)为适应度函数。
不同人工鱼个体相距位置定义为
人工鱼群算法搜索过程包括以下部分[ 9-10 ]:
1)觅食行为,其状态定义为
式中:V为人工鱼的视野范围;V为区间[-1,1]之间随机数。
如果Xj位置食物浓度高于Xi,则人工鱼就会向Xj位置移动一步,即为觅食行为,如下所示
式中:s为移动步长;t为迭代次数。
2)聚群行为,在人工鱼为Xi位置时,d 如果XC位置适应度较好,则向XC位置聚集,否则继续觅食,如下所示 3)追尾行为,寻找视野区间中优秀个体,若Xj位置适应度较好,并且不太拥挤,则向其Xj处移动,否则继续觅食,如下所示 4)随机行为,当迭代次数达到最大值,仍然没有搜索到最优值,就会产生随机行为,如下所示 采用人工鱼群算法流程图如图2所示。 2.2 RBF控制器优化 RBF神经网络采用多输入单输出的网络结构,能够逼近任意连续的函数,具有较好的控制效果。RBF神经网络采取的函数为高斯基函数[ 11 ],如下所示 式中:x = [x1,x2,…,xn]T为输入向量;cj = [cj1,cj2,…,cjn]为中心矢量;bj为基宽度参数。 在RBF神经网络控制器中,其权向量定义为 控制器网络输出函数[ 11 ]定义为 两轮机器人控制目标函数可以定义为 采用梯度下降法[ 11 ],不同参数迭代算法定义为: 式中:α为动量变化因子;η为学习速率。 采用人工鱼群算法对RBF神经网络控制器进行优化,将优化后的控制器用于两轮机器人中,其优化控制流程如图3所示。 3 仿真与分析 为了验证两轮机器人优化后的控制效果,进行仿真实验,比较优化前和优化后的机器人运动误差,从而体现出人工鱼群算法优化后的优越性。假设两轮机器人起始位置坐标为(0,0),终点位置坐标为(1000,1000)。在相同环境中,横向跟踪误差如图4所示,纵向跟踪误差如图5所示。 根据图4可知,优化前,两轮机器人横向输出误差范围在-3 mm至3 mm之间,变化幅度较大。优化后,两轮机器人横向输出误差范围在-2 mm至2 mm之间,变化幅度较小。 根据图5可知,优化前,两轮机器人纵向输出误差范围在-3 mm至3 mm之间,变化幅度较大。优化后,两轮机器人纵向输出误差范围在-2 mm至2 mm之间,变化幅度较小。 对比优化前和优化后的两轮机器人控制效果,优化后输出误差明显低于优化前。优化前的RBF神经网络控制器,机器人横向和纵向输出误差相差不大;优化后的RBF神经网络控制器,机器人横向和纵向输出误差相差不大。但是RBF神经网络控制器采用人工鱼群算法优化后,控制精度得到了提高,优势相对明显。因此,采用人工鱼群算法优化RBF神经网络控制器,可以使两轮机器人定位更加精确,适合机器人高精度移动的场合。 4 结语 针对两轮机器人跟踪误差较大问题,设计了RBF神经网络控制器,采取人工鱼群算法对控制器进行优化,将优化后的控制器进行仿真验证。实验结果表明:优化前,两轮机器人横向和纵向跟踪误差在-3 mm至3 mm之间,优化后,两轮机器人横向和纵向跟踪误差在-2 mm至2 mm之间。优化后,两轮机器人运动轨迹跟踪误差降低了,证明了人工鱼群算法具有较好的搜索功能,能够提高两轮机器人运动精度,为后期从事两轮机器人研究人员提供参考方法。 参考文献: [1] 陶言侃.双轮自平衡机器人设计及轨迹跟踪控制研究[D].哈尔滨:哈尔滨工业大学,2019. [2] 李巧艺.酒店服务机器人结构设计与运动控制研究[D].成都:西南交通大学,2017. [3] 闫辉,贾彦茹,董建军.一种两轮自平衡机器人比例-积分-微分控制方法[J].自动化技术与应用,2021,40(3):6-10. [4] Carlucho I, Paula M D, Villar S, et al. Incremental q-learning strategy for adaptive pid control of mobile robots[J].Expert Systems With Applications, 2017,80:183-199. [5] 黎小巨,殷素峰,陳洵凛,等.两轮自平衡机器人姿态误差的神经网络补偿研究[J].机床与液压,2020,48(15):44-49. [6] Hoang N B, Kang H J. Neural network-based adaptive tracking control of mobile robots in the presence of wheel slip and external disturbance force[J].Neurocomputing,2016,188:12-22. [7] 夏国清,陈华珍.模糊理论和PID相融合的两轮自平衡机器人智能控制系统[J].现代电子技术,2018,41(21):117-120. [8] Begnini M, Bertol D W, Martins N A. A robust adaptive fuzzy variable structure tracking control for the wheeled mobile robot: simulation and experimental results[J].Control Engineering Practice, 2017,64: 27-43. [9] 姚正华.改进人工鱼群智能优化算法及其应用研究[D].徐州:中国矿业大学,2016. [10] Costa F P M, Rocha M A C A, Fernandes M G P E. An artificial fish swarm algorithm based hyperbolic augmented lagrangian method[J].Journal of Computational and Applied Mathematics, 2014,259:868-876. [11] 申爱民,贺严松.用于车辆非线性液压悬架的径向基函数神经网络控制优化与仿真[J].中国工程机械学报,2020,18(2):148-152. [责任编辑:郑笔耕]
