基于自表示的双图规格化特征选择聚类

汪宏海，吴 樱

基于自表示的双图规格化特征选择聚类

*汪宏海1,2，吴 樱1,2

（1.浙江省文化和旅游发展研究院，浙江，杭州 311231；2.浙江旅游职业学院，浙江，杭州 311231）

特征选择得到的识别特征可以用于聚类分析，提高聚类分析的质量。受数据自表示特性和双图规则化学习的启发，提出了一种新的特征选择聚类算法。利用数据和特征的自表示特性，不仅保留了数据的流形信息，而且保留了特征空间的流形信息。此外，为了充分发挥双图模型的作用和鉴别局部聚类的效果，加入局部判别特征选择聚类，大大提高了聚类的有效性和鲁棒性。

特征选择；自表示；双图规格化；聚类

0 引言

大数据中存在着高维数据。这些高维的数据不仅数据维度非常大，冗余的数据也非常多。数据降维可以降低数据的维度，排除一些冗余复杂的噪声数据集[1]。数据降维的方法主要有两种：特征选择和特征提取。特征选择是从原始的众多特征中，选择出具有代表性质的特征，由于是从原始的特征集合中筛选出来的特征集，所以不会破坏原有的数据，并且具有解释性强的优点[2]。本研究主要关注特征选择。特征选择按照使用标签信息的方式，可分为监督、半监督、非监督算法。由于现实中很多数据没有标签信息，因此，非监督特征选择具有更广泛的应用[3-4]。

在特征选择领域中，根据选择思想的不同，选择方法可以分为过滤法(filter)、包裹式(wrapper)、嵌入式(embedding)[5]。Embedding方法由于结合了机器学习的思想，具有较好的效果[6]。很多非监督特征选择算法用来做聚类，由于在选择后获得表示特征用于聚类，因此，聚类质量得到了加强[7]。在Embedding方法的研究中，目前较为成熟且较为广泛使用的方法，基本上都是基于将流形学习与NMF思想结合的算法，比如拉普拉斯评分（Laplacianscore：LapScore）[8]、谱特征选择（SPEC： spectral feature selection[9]，多类簇特征选择（MCFS：Feature Selection For Multi-cluster Data）[10]，最小冗余谱特征选择算法(MRSF:Spectral Feature Selection with Minimum Redundancy)[11]，联合嵌入式学习和稀疏回归的特征选择(JELSR:Joint embedding Learning and Sparse)[12]，局部性和相似性保留嵌入特征选择(LSPE：locality and similarity preserving embedding feature selection)[13]。

已有的算法中，LapScore只保留数据流形的位置，但是没有学习机制和迭代更新机制；SPEC可以看作是LapScore的扩展，但主要用于监督特性选择，并不适用于无监督特征选择；考虑到不同集群之间的关系，MCFS保留了数据集的多集群结构。JELSR将嵌入式学习和稀疏回归统一到一个无监督的特征选择框架中，利用学习后的稀疏投影矩阵进行特征选择。MRSF是基于稀疏多输出模型来最小化冗余特性的。LSPE将嵌入式学习和特征选择集成在一个联合框架中。总之，上述特征选择算法都是在数据流形空间中进行的，有些保持局部信息，有些保持相似性以提高学习性能，都缺少了对数据表示特征的有效使用。

基于此，受自表示特性和双图规则化学习的启发，提出一种新的特征选择聚类算法。本算法不使用投影矩阵，而是利用数据和特征的自表示特性，在数据空间中使用自表示系数矩阵作为特征自表示构造的重要度量，利用数据空间中的自表示系数矩阵对特征进行排序。不仅保留了数据的流形信息，而且保留了特征空间的流形信息。此外，加入局部判别特征选择聚类，可以大大提高聚类的有效性和鲁棒性。

2 本文算法

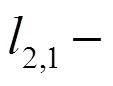
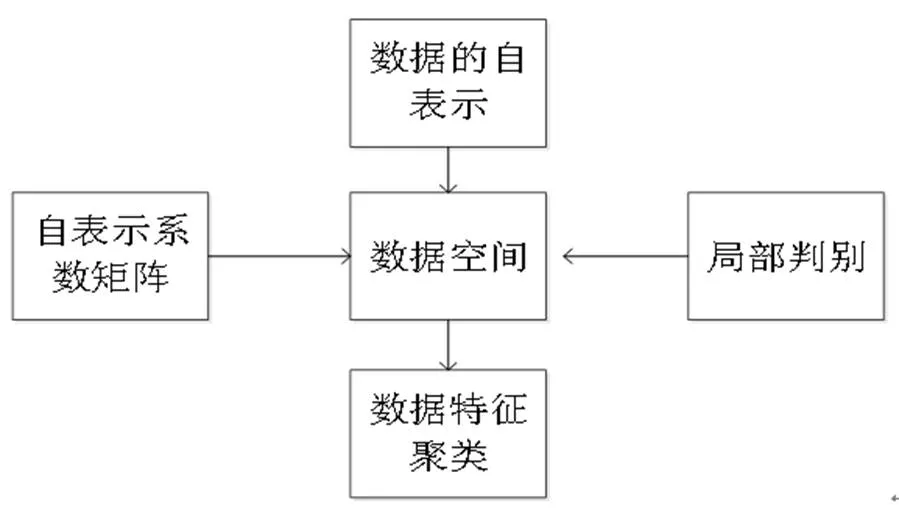
图1 数据处理过程

2.1 关键技术

本算法中，数据点和特征是通过利用自表示来表示的。对于每个向量x，通过自表示属性，可以由中的所有特征表示，即1;2; …;x来表示。可以得出：

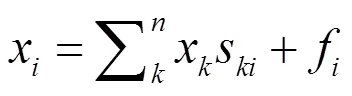
(2)

类似的，在数据空间，可以得到：

XT=XTP+H (3)

将自表示重构误差最小化，即解决如下问题：

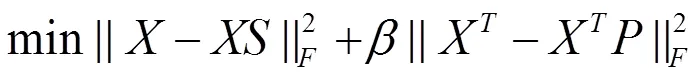
其中，参数（≥0）平衡这两个自表示的错误项。

在数据空间和特征空间中构造两个邻域图来保存局部几何信息，即数据图和特征图。在数据空间中构造最近的邻域图G，图中的每个节点对应一个数据点。如果两个数据点位于个最近的邻域内，则设置一条边。两个数据点之间的相似性作为边缘权重。选择0-1加权方案作为权重函数。

0-1权重方案定义如下：

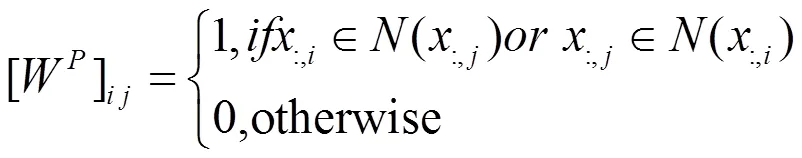
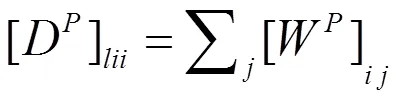
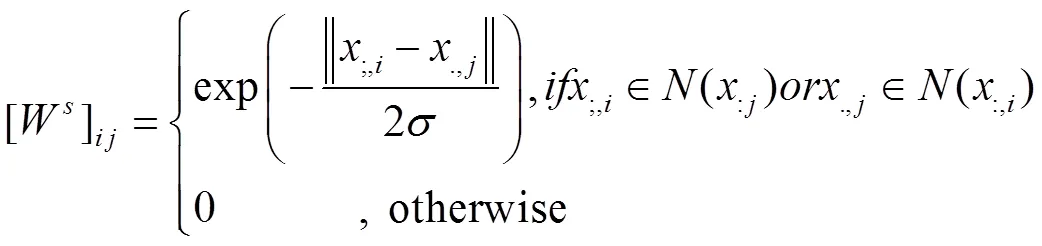
特征图的拉普拉斯算子矩阵是L=D-W，其中D是一个对角矩阵，并且

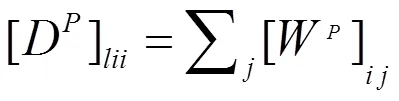
X=11i+22i+…+XS

X=11j+22j+…+XS

把的第列和第列表示为

S=[1i,2i,…,S]

S=[1j,2j,…,S]

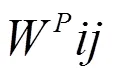
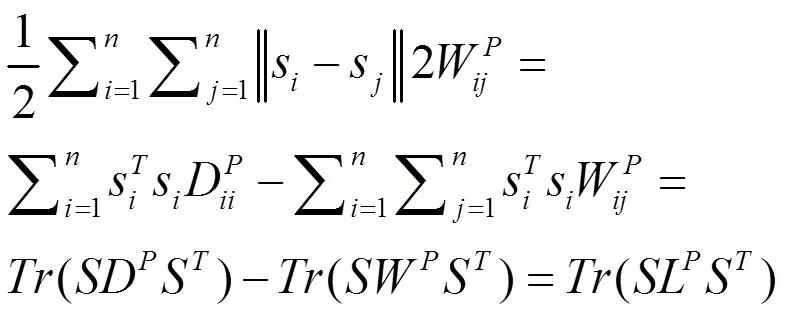
同样，考虑到数据空间的自表示矩阵和相似矩阵W，可以得到以下的数据表示平滑度：

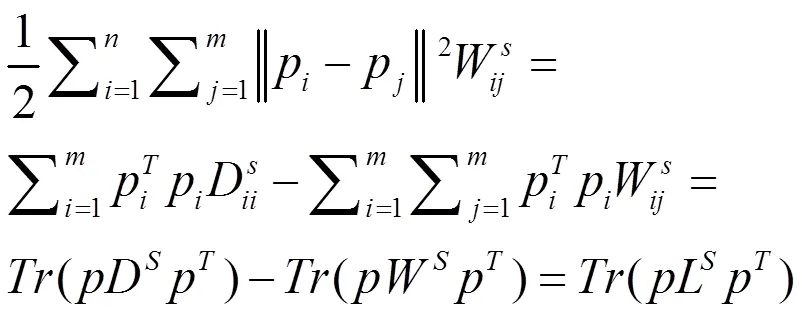
在上述数据图和特征图的基础上，利用自表示特性，同时考虑数据空间和特征空间的多种信息，寻求一个在数据空间和特征空间中都具有的准确表示。因此，本算法解决以下最小化问题：

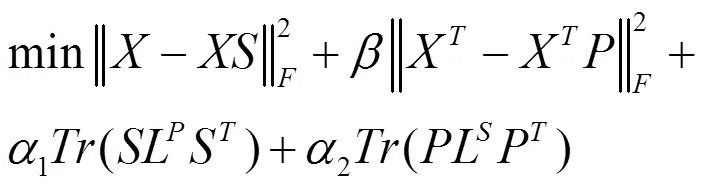
,≥0 (9)

上式中，>0,1>=0,2>0。为了简单和方便，让1=1=，这样，目标函数就可以改写为：

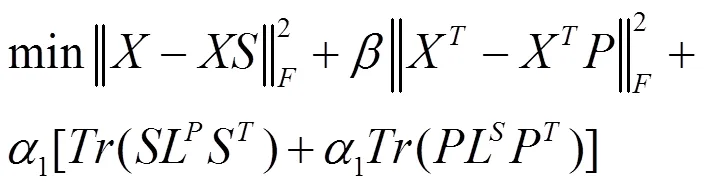
,≥ 0 (10)

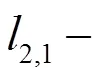
因此，本问题即是：

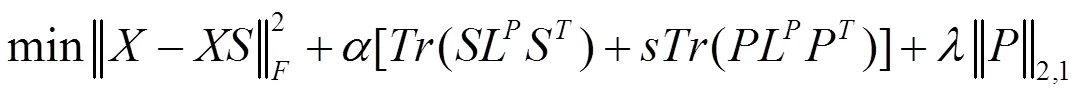
≥ 0 (11)

参数λ（λ ≥ 0）平衡最后稀疏的项目。此式子通过迭代的方式进行求解。

2.2 融入LDC（local density clustering）的聚类算法

根据预先设置的聚类数，将聚类分为若干部分，使同一类元素的相似性尽可能大，使不同类元素的相似性尽可能小。在上面的算法中，根据||P||的值按降序选取数据集的前个特征，从而在特征选取后得到矩阵X= [1,2，…，]∈×。然后，对数据集X进行聚类。将数据集X划分为聚类簇，得到标记矩阵= [1,2，…，m]∈{0,1}×c。m的第个元素是m，如果X∈C，则m= 1，否则为0。

首先定义一个矩阵Z：

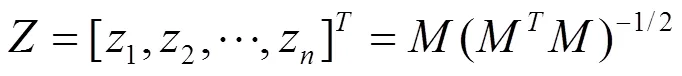
其中Z为数据向量习的聚类赋值向量。由于MM是一个对角矩阵，可以很容易地得出结论：

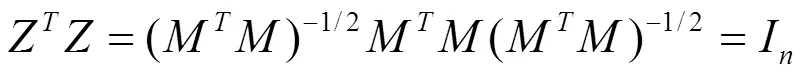
定义簇间散射矩阵S、簇内散射矩阵S和总散射矩阵S如下：

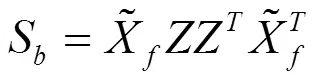
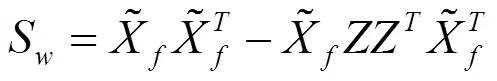
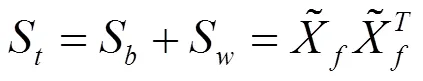
．>0 (17)

由于式(13)中ZZ = I，可以通过最小化以下目标得到最佳的聚类分配矩阵Zbest功能：

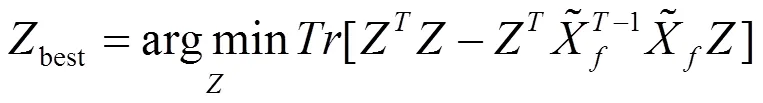
> 0 (18)

由于数据的局部流形信息类似于线性，采用由数据点x的个最近邻组成的局部团N(x)，其中包含数据点x本身及其(- 1)个最近邻。因此，建立了一个局部线性判别模型来评价聚类结果。

定义一个矩阵X= [x1,x2，…，x]，其中包含局部分N(x)中的所有数据点，并将对应的索引集定义为= {1,2，…,i}。同样，根据局部线性判别模型，定义1= [11,12，…，1k]∈×，由矩阵簇Z按照下式计算得到：

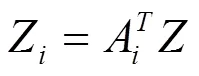
> 0 (20)

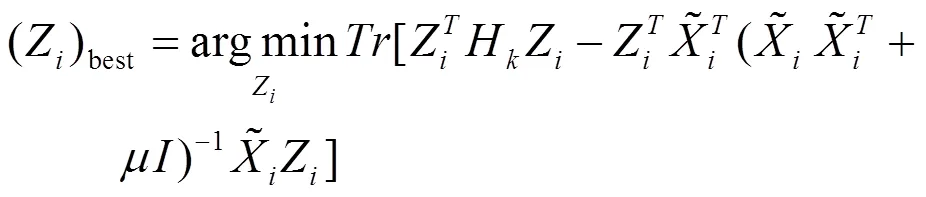
> 0 (21)

因为：

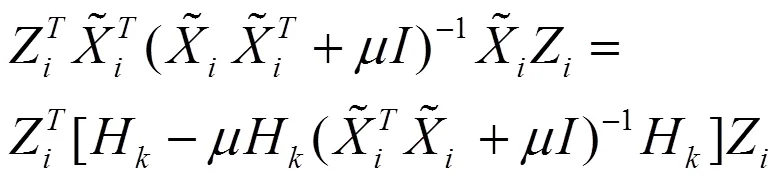
因此，公式（21）就可以转化为：

> 0 (23)

把上式改为：

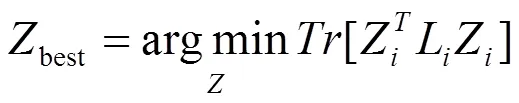
其中：

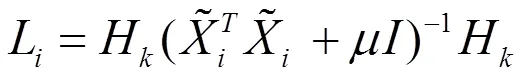
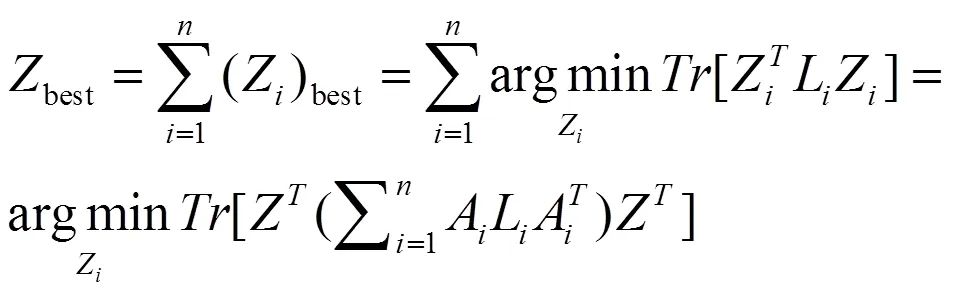
定义

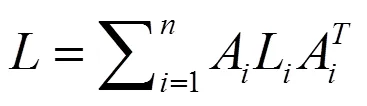
那么上式就可以写作：

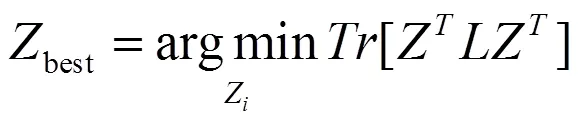
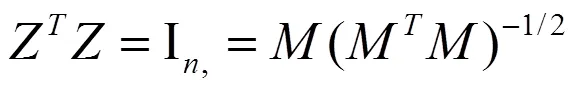
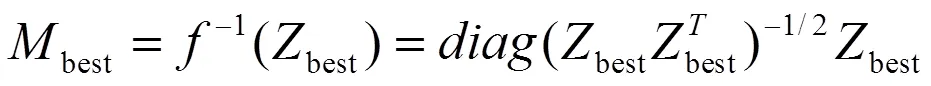
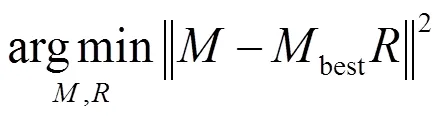
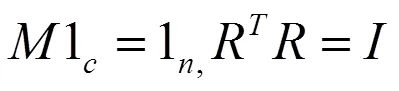
2.3 具体算法流程

本文算法分为以下10个步骤：

Step1．加载数据矩阵。

Step2．计算出数据矩阵的特征空间的非负矩阵因子，数据空间的非负矩阵因子，初始化矩阵，，。

Step3.根据迭代更新规则（5），(9)和（10）更新矩阵，和。

Step 4.根据||P||2的值按降序选取前个特征。

Step 5.构造每个数据点的局部小圈子。

Step 6.根据式(24)计算L，通过全局积分求解式(26)中的拉普拉斯矩阵。

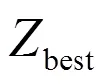
Step 9．通过连续迭代优化得到二值聚类分配矩阵M。

Step 10．最后，通过评价指标计算出ACC和NMI输出结果。

3 实验及数据分析

3.1 数据集及参数设置

实验中验证了在5个数据集上，本文算法和其他特征选择算法的比较结果，并对结果进行了分析。5个数据集分别为：UMIST图像集，包括20个人共575幅图像，每个人具有不同角度、不同姿态的多幅图像；ORL图像集包括40人，共400张面部图像；BC数据集包括2类569个数据；Ionosphere是一个经典的二元分类问题，共有351个观测值，34个输入变量；Dbworld_bodies包含2类64个数据。实验比较的算法包括LapScore[8]、SPEC[9]、MCFS[10]、MRSF[11]、JELSR[12]、LSPE[13]。

表1 数据集

Table 1 Data set

数据集维度大小类数 UMIST64457520 ORL102440040 BC305692 Ionosphere343512 Dbworld_bodies4702642

实验中参数的设置如下：LSPE、LapScore、SPEC和MCF，邻居数选自{3,5,10,15}，σ的内核权重选自{1,103,105}。本算法的正则参数α选自{0.01,0.1,0.5,1.0,5.0,9.0,13.0,17.0}，β选自{100, 1000}，λ选自{300,800,2000,4000,6000,8000}。常规参数α选自{0.01,0.1,0.5,1.0,5.0,9.0,13.0,17.0}，β和θ选自{300,800,2000,4000,6000,8000}，μ选自{10−8,10−6,10−4,10−2,100,102,104,106,108}。

3.2 评价指标

用两个广泛使用的评价矩阵来评价聚类的性能。聚类精度(ACC)，归一化互信息(NMI)。ACC和NMI值越大，说明性能越好。

给定数据点，c和g分别为的聚类标签和有效真实标签。

ACC的定义如下：

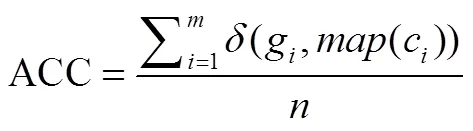
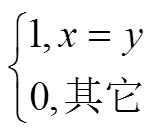
NMI的定义如下：

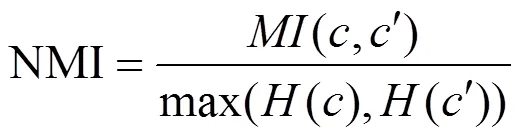
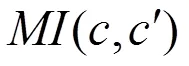
NMI是评价聚类标签之间的相似性程度的一种外部准则，它评估了聚类标签和基本真实标签之间的相似程度。ACC和NMI是两个聚类评估标准，它们可能无法同时在一个数据集中获得最佳效果。

3.3 实验结果

实验记录了最优参数的最佳聚类结果。表2显示了5个数据集的平均ACC和标准偏差，用粗体突出显示最佳结果。

3.3.1 本文算法实验结果

表2 相关算法ACC

Table 2 ACC of related algorithms

算法UmistORLIonosphereBCDbworld_bodies LapScore37.30 ± 0.9344.50 ± 0.7366.94 ± 2.2070.17 ± 0.3673.47 ± 1.16 SPEC42.56 ± 1.2049.88 ± 0.2367.70 ± 2.3374.00 ± 0.2377.94 ± 1.85 MCFS46.55 ± 1.0049.40 ± 0.9357.26 ± 3.0071.00 ± 0.5891.13 ± 1.04 JELSR48.90 ± 1.0350.02 ± 0.5667.90 ± 2.8174.20 ± 0.3090.63 ± 0.00 MRSF48.38 ± 1.0549.78 ± 0.6963.00 ± 2.3072.9 ± 0.2285.02 ± 1.59 LSPE49.26 ± 1.1250.25 ± 0.8070.00 ± 2.6675.86 ± 0.2493.75 ± 0.00 本文算法61.21 ± 2.2560.71 ± 1.5188.79 ± 2.3775.55 ± 0.0095.68 ± 0.014

表3显示了5个数据集的NMI，用粗体突出显示最佳结果。

表3 相关算法NMI

Table 3 NMI of related algorithms

算法UmistORLIonosphereBCDbworld_bodies LapScore56.32 ± 1.5267.80 ± 1.76 8.16 ± 0.0016.79 ± 0.0023.82 ± 1.01 SPEC57.04 ± 1.2470.26 ± 1.65 8.33 ± 0.0018.83 ± 0.0025.20 ± 1.62 MCFS69.20 ± 1.3170.98 ± 1.78 1.01 ± 0.7717.32 ± 0.0067.88 ± 1.62 JELSR70.18 ± 1.6470.20 ± 1.72 7.84 ± 1.2118.86 ± 0.0054.89 ± 0.00 MRSF66.67 ± 1.4370.50 ± 1.81 3.82 ± 0.0017.32 ± 0.0056.79 ± 2.39 LSPE70.01 ± 1.5071.04 ± 1.1113.10 ± 0.4918.83 ± 0.0068.09 ± 0.00 本文算法70.51 ± 1.5275.25 ± 1.3323.12 ± 0.5730.99 ± 0.0059.99 ± 1.27

从表2和表3中，可以看到：本文算法优于其他算法，在几乎所有数据集的聚类精度方面都取得了较好的结果，尤其是在处理面部数据的时候。与其他特征选择算法相比，本算法的主要改进之处在于它利用了特征空间的自表示特性，特征空间中的信息对于聚类是非常重要的。SPEC, MCFS和MRSF是两阶段的特征选择算法，而JELSR，LSPE和本文算法同时集成多种策略。JELSR将嵌入式学习和稀疏回归相结合，LSPE将嵌入式学习和特征选择相结合，本算法将自表示、流形嵌入和特征选择相结合。总体上，JELSR、LSPE的聚类质量优于其他算法，说明同时求解多个问题优于按顺序求解。LSPE是实验中第二好的算法，也说明了将嵌入学习和特征选择结合起来进行特征选择是一种较好的方法。

3.3.2 没有加入局部判别的算法效果

为了更清楚的体现局部判别的对算法结果的影响，在不加入局部判别的情况做了相关实验，表4显示了5个数据集ACC结果，表5显示了5个数据集NMI结果。

表4 相关算法ACC（无局部判别）

Table 4 ACC of related algorithms （without local discrimination）

算法UmistORLIonosphereBCDbworld_bodies LapScore37.30 ± 0.9344.50 ± 0.7366.94 ± 2.2070.17 ± 0.3673.47±1.16 SPEC42.56 ± 1.2049.88 ± 0.2367.70 ± 2.3374.00 ± 0.2377.94±1.85 MCFS46.55 ± 1.0049.40 ± 0.9357.26 ± 3.0071.00 ± 0.5891.13±1.04 JELSR48.90 ± 1.0350.02 ± 0.5667.90 ± 2.8174.20 ± 0.3090.63±0.00 MRSF48.38 ± 1.0549.78 ± 0.6963.00 ± 2.3072.9 ± 0.2285.02±1.59 LSPE49.26 ± 1.1250.25 ± 0.8070.00 ± 2.6675.86 ± 0.2493.75±0.00 本文算法58.68 ± 2.6957.64 ± 1.8485.45 ± 2.5875.24 ± 0.0994.70±.021

表5 相关算法NMI（无局部判别）

Table 5 NMI of related algorithms（without local discrimination）

算法UmistORLIonosphereBCDbworld_bodies LapScore56.32 ± 1.5267.80 ± 1.76 8.16 ± 0.0016.79 ± 0.0023.82 ± 1.01 SPEC57.04 ± 1.2470.26 ± 1.65 8.33 ± 0.0018.83 ± 0.0025.20 ± 1.62 MCFS69.20 ± 1.3170.98 ± 1.78 1.01 ± 0.7717.32 ± 0.0067.88 ± 1.62 JELSR70.18 ± 1.6470.20 ± 1.72 7.84 ± 1.2118.86 ± 0.0054.89 ± 0.00 MRSF66.67 ± 1.4370.50 ± 1.81 3.82 ± 0.0017.32 ± 0.0056.79 ± 2.39 LSPE70.01 ± 1.5071.04 ± 1.1113.10 ± 0.4918.83 ± 0.0068.09 ± 0.00 本文算法70.36 ± 1.6574.14 ± 1.4521.76 ± 0.7330.13 ± 0.0858.24 ± 1.38

从表4和表5的结果可以看出，本文提出的算法即使在没有局部判别信息的情况下，总体效果也优于相关算法。但与加入局部判别信息的本最终算法比较，效果略微差一些，方差变大。因此，说明了加入局部判别，可以提高聚类的有效性和鲁棒性。

4 结论

本研究提出了一种自表示的双图规格化特征选择聚类算法，不仅保留了数据的流形信息，而且保留了特征空间的流形信息。此外，加入局部判别特征选择聚类，可以大大提高聚类的有效性和鲁棒性。

[1] 机器学习中的特征选择方法研究及展望[J].北京邮电大学学报, 2018(1):1-12.

[2] 谢娟英,丁丽娟,王明钊.基于谱聚类的无监督特征选择算法[J].软件学报,2020,56(1):20-32.

[3] Meng Y,Shang R,Jiao L,et al.Feature selection based dual-graph sparse non-negative matrix factorization for local discriminative clustering[J].Neurocomputing,2018，32(3)：1783-1796.

[4] Shang R,Wang W,Stolkin R,et al.Non-Negative Spectral Learning and Sparse Regression-Based Dual-Graph Regularized Feature Selection[J]. IEEE Transactions on Cybernetics,2017,45(6):1-14.

[5] Meng Y,Shang R,Jiao L,et al.Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints[J].Engineering Applications of Artificial Intelligence,2018, 69:24-35.

[6] Hou C, Nie F, Li X, et al. Wu,Joint embedding learning and sparse regression:a framework for unsupervised feature selection[J]. IEEE Trans on Cybernetics, 2014,44 (6):793-804.

[7] Zhu X Y. Improved Algorithm Based on Non-negative Low Rank and Sparse Graph for Semi-supervised Learning[J].Journal of Electronics & Information Technology,2017,10(4):1123-1128.

[8] Tian S,Zhang Y,Yan Y.ℓ1/2-norm regularized nonnegative low-rank and sparse affinity graph for remote sensing image segmentation[J].Journal of Applied Remote Sensing,2016,10(4):042008.

[9] Zhao Z, Wang L, Liu H. Efficient spectral feature selection with minimum redundancy[C]. Proceedings of 24th AAAI Conference on Artificial Intelligence, 2010:673-678.

[10] Zhao Z, Liu H.Spectral feature selection for supervised and unsupervised learning[C]. Machine Learning, Proceedings of the Twenty-Fourth International Conference (ICML 2007),2007.

[11] Cai D, Zhang C, He X. Unsupervised feature selection for multi-cluster data[C]. Acm Sigkdd International Conference on Knowledge Discovery & Data Mining, ACM, 2010.

[12] Li Z,Tang J.Unsupervised Feature Selection via Nonnegative Spectral Analysis and Redundancy Control[J].IEEE Transactions on Image Processing,2015, 24(12):5343-5355.

[13] Fang Y,Xu X,Li Z.Locality and similarity preserving embedding for feature selection[J]. Neurocomputing, 2014,128:304-315.

[14] Zhu X Y, Wang Y, Li Y B. A new unsupervised feature selection algorithm using similarity-based feature clustering.[J] Computational Intelligence,2019, 47(1):161-173.

[15] 方佳艳,刘峤.具有同步化特征选择的迭代紧凑非平行支持向量聚类算法[J].电子学报,2020，56(1):20-32.

[16] Yang Y, Xu D, Nie F, et al. Image clustering using local discriminant models and global integration[J].IEEE Trans. Image Process. 2010,19(10): 2761-2773.

[17] Wu S S, Hou M X, Feng C M. LJELSR: A Strengthened Version of JELSR for Feature Selection and Clustering[J]. International journal of molecular sciences,2018, 22(8):888-905.

[18] Ahmad AliyuUsman,Starkey Andrew.Application of feature selection methods for automated clustering analysis:a review on synthetic datasets[J].Neural computing and applications,2018,56(3):115-119.

FEATURE SELECTION CLUSTERING BASED ON SELF-REPRESENTING DOUBLE GRAPH NORMALIZATION

*WANG Hong-hai1,2，WU Ying1,2

(1. Zhejiang Institute of Culture and Tourism Development, Hangzhou, Zhejiang 311231, China; 2. Tourism College of Zhejiang, Hangzhou, Zhejiang 311231, China)

The recognition features obtained through feature selection can be used in cluster analysis to improve the quality. Inspired by the self-representation characteristics of data and regular learning of double graphs, a new feature selection clustering algorithm was proposed. Utilizing the self-representation characteristics of data and features, not only the manifold information of the data but also the manifold information of the feature space was retained. In addition, in order to make the dual graph model work at full capacity, and identify the effects of local clusters, we added the local discriminative features for clustering, which had greatly improved the effectiveness and robustness of clustering.

feature selection; self-representation; double graph normalization; clustering

TP18

A

10.3969/j.issn.1674-8085.2021.02.013

1674-8085(2021)02-0076-07

2020-09-23；

2020-11-09

*汪宏海(1977-），男，江西樟树人，副教授，硕士，主要从事算法优化、图像处理等方面的研究(E-mail:redsea54@163.com);

吴 樱(1980-），女，浙江杭州人，讲师，硕士，主要从事酒店人力资源管理、酒店数字化运营等方面的研究(E-mail:652348105@qq.com).