一类分数阶比率依赖型捕食系统的动力学分析

蒲武军，杜争光

一类分数阶比率依赖型捕食系统的动力学分析

*蒲武军，杜争光

（陇南师范高等专科学校数学系，甘肃，陇南 742500）

讨论了一类食饵带有疾病的分数阶比率依赖型捕食系统的动力学行为。利用线性化方法定性分析了各类平衡点的稳定性，并给出了其正平衡点局部渐近稳定的充分条件。数值模拟显示，参数和阶数对平衡点的收敛速度及其稳定性产生很重要的影响。

分数阶；比率依赖型捕食系统；局部渐近稳定性；Hopf分支

近年来，随着计算机技术的不断发展，分数阶计算引起了许多学者的关注，并成功应用到工程技术领域[1-2]，特别是许多应用数学工作者[3-7]用分数阶计算模拟现实过程。靳桢[8]研究了一类食饵带有疾病的比率依赖型捕食系统，讨论了其平衡点的稳定性。受此启发，本文考虑如下分数阶模型：

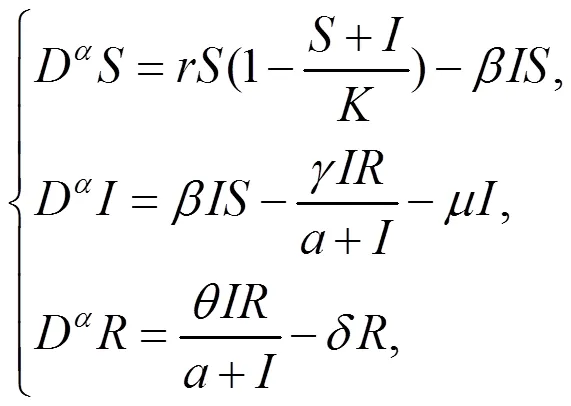
1 预备知识

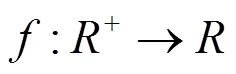
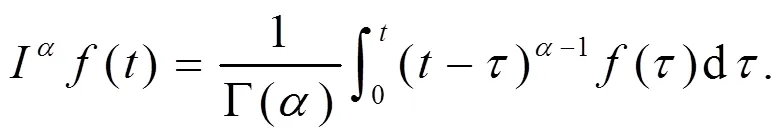
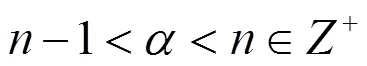
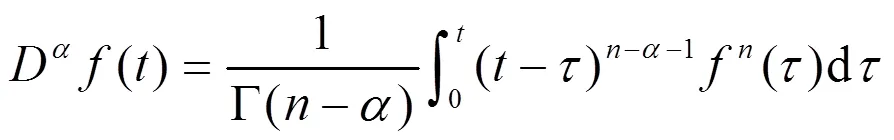
引理1[10]考虑如下的自治系统：

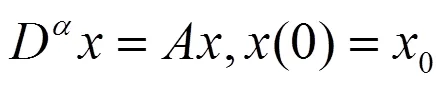
引理2[11]考虑如下的分数阶系统：

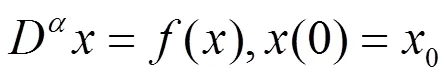
2 主要结果及其证明

2.1 解的存在唯一性

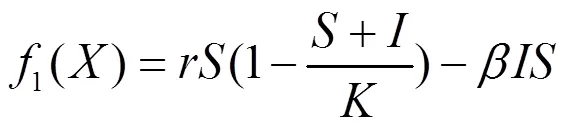
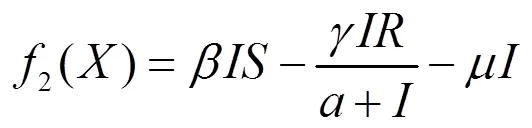
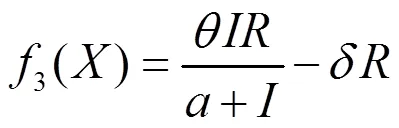
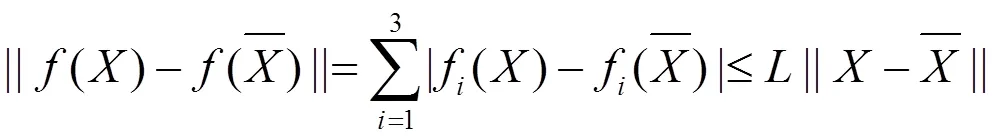
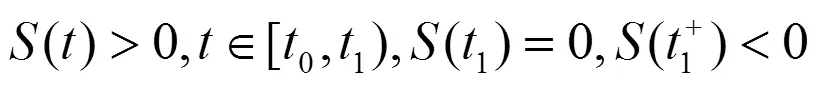
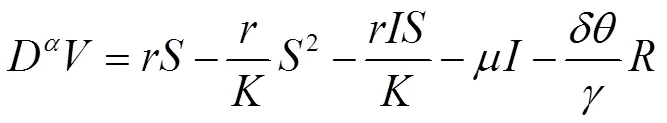
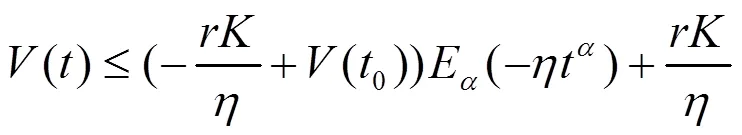
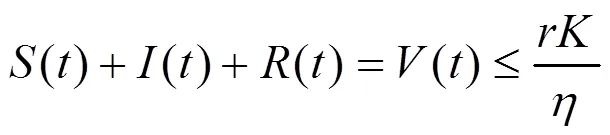
2.2 平衡点的局部稳定性

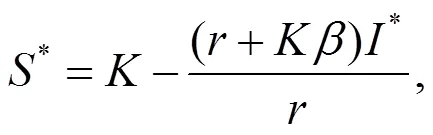
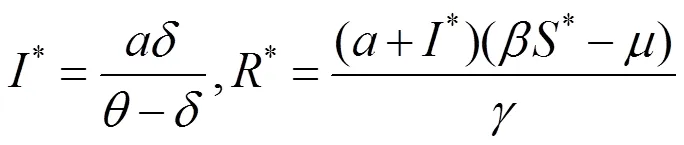
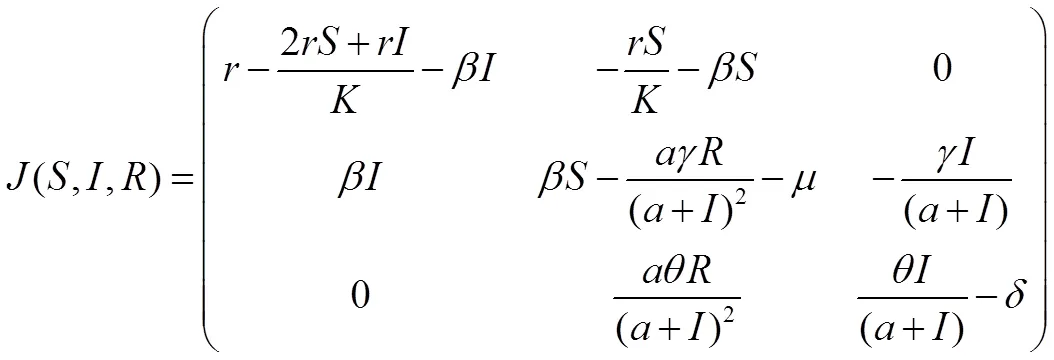
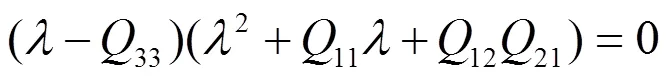
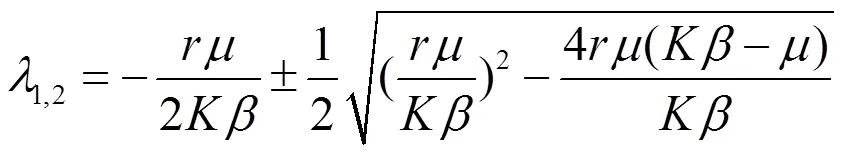
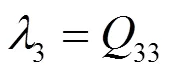
情形1：

情形2：

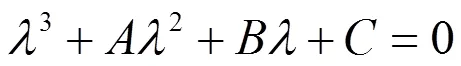
方程(8)三个特征根可表示为

其中

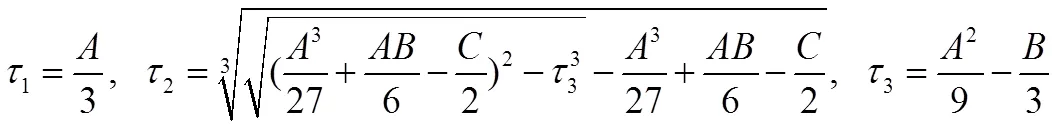
证明：结论(i)和(iii)显然成立，故只需证明结论(ii)成立即可，注意到

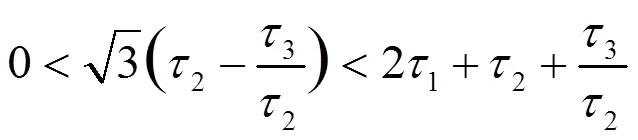
3 数值模拟

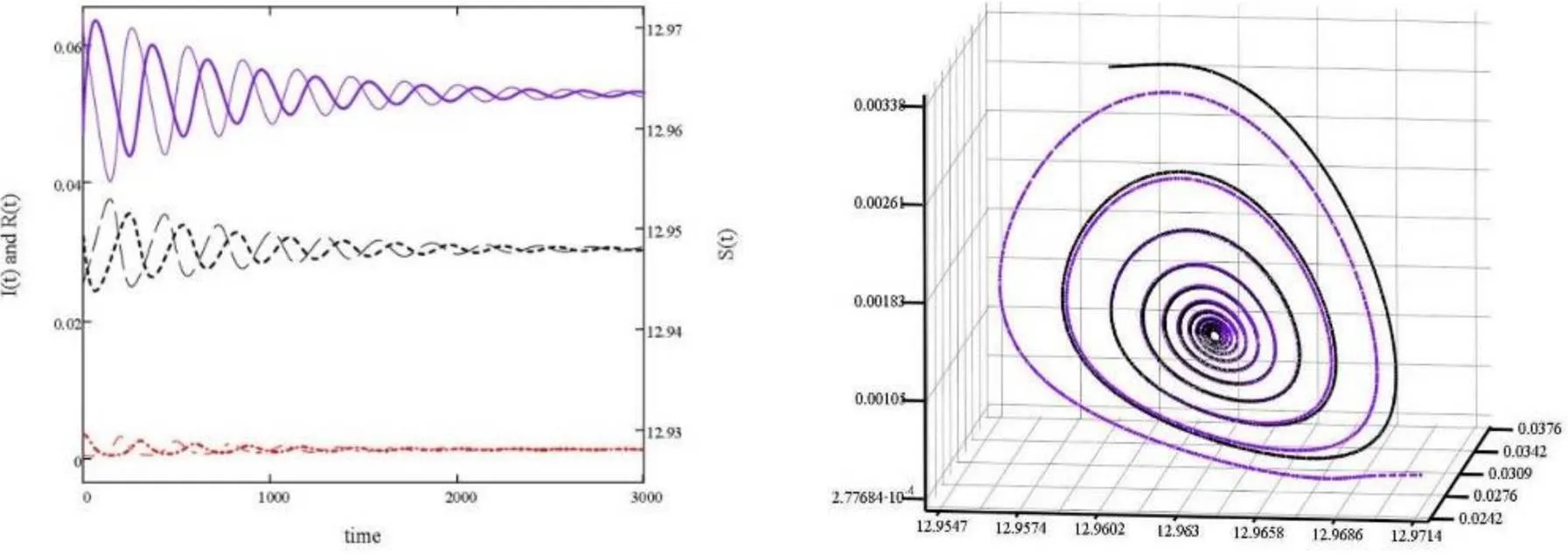
图1 易感者S，感染者I，捕食者R的收敛性及其相图

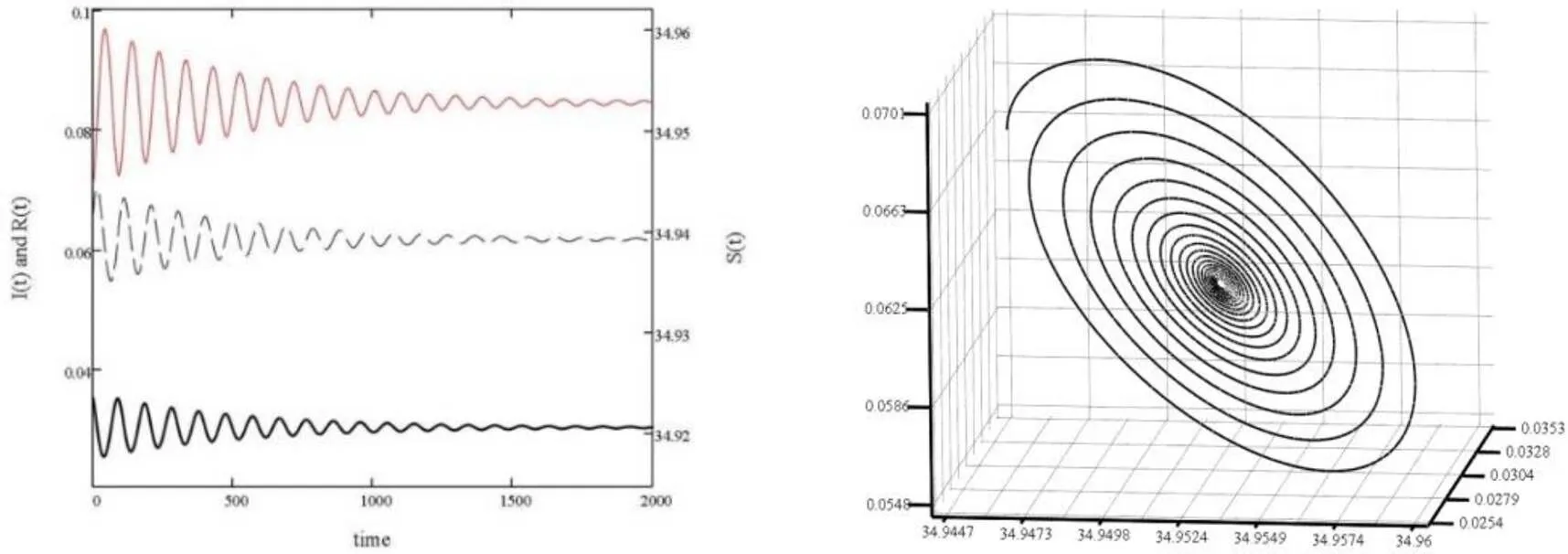
图2 不同参数下易感者S，感染者I，捕食者R的收敛性及其相图

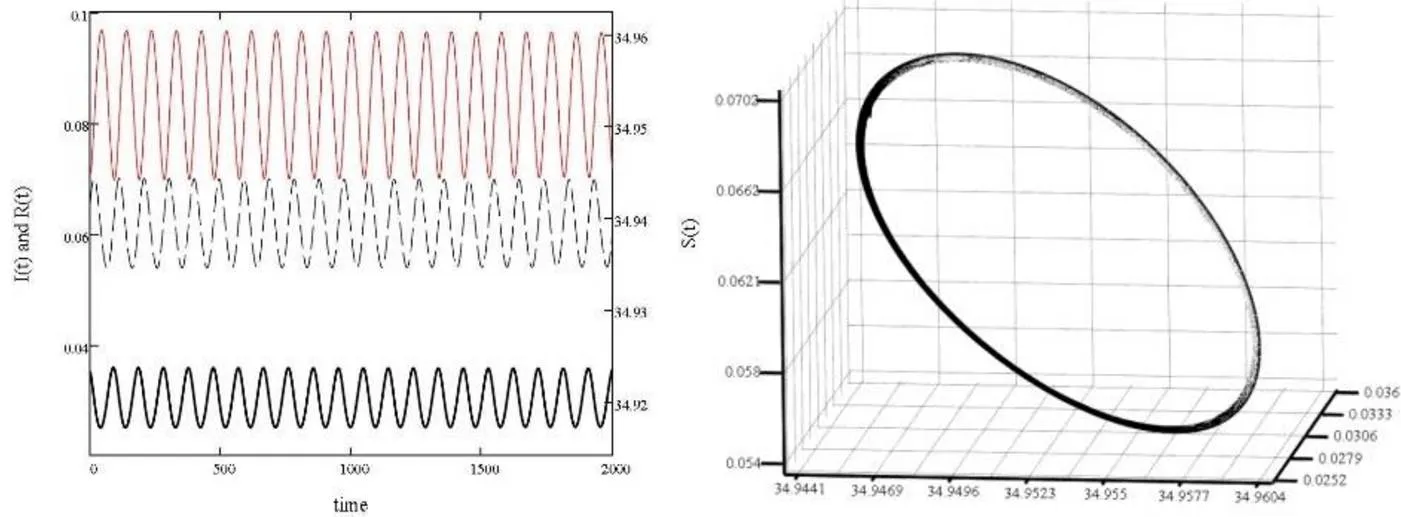
图3 α=0.988时，易感者S，感染者I，捕食者R的振荡及正平衡点附近的周期性闭轨

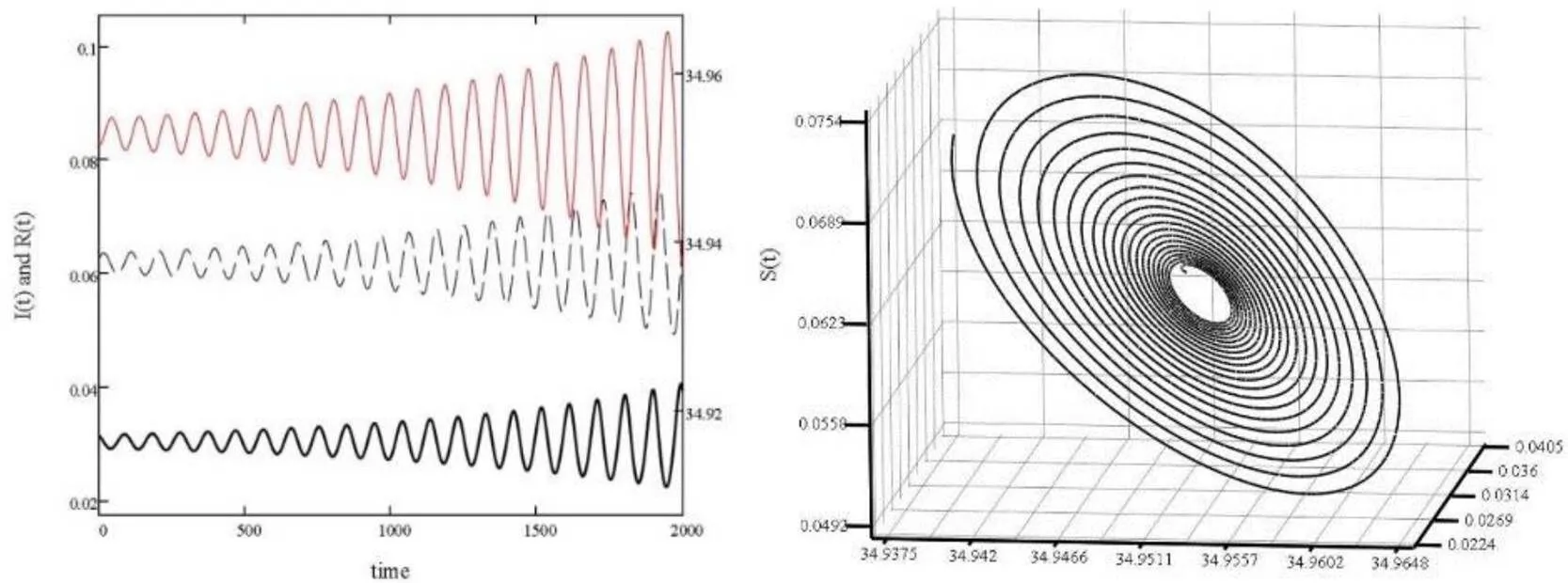
图4 α=0.988时，易感者S，感染者I，捕食者R发散及正平衡点不稳定

4 讨论

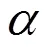
[1] Laskin N.Fractional market dynamics[J] .Physica A，2000,287(3):482-492.

[2] Duarte F B, Machado J T. Chaotic phenomena and fractional-order dynamics in the trajectory control of redundant manipulators[J] . Nonlinear Dynam,2002,29 (1–4):315-342.

[3] Bozkurt. F, Yousef A. Flip bifurcation and stability analysis of a fractional-order population dynamics with Allee effect[J] .Journal of Interdisciplinary Mathematics，2019,22(6):1035-1050.

[4] 蒲武军,杜争光.一类分数阶广义捕食者-食饵模型的动力学分析[J].西北师范大学学报:自然科学版,2018, 5:10-15.

[5] 刘娜,方洁,邓玮,等. 一类分数阶复值SIR传染病模型的稳定性分析[J].数学的实践与认识,2019,23:256-261.

[6] 赵新俊,郑义. 分数阶SIR传染病模型的稳定性分析[J]. 生物数学学报,2018,1:11-16.

[7] 杜争光. 具有Holling Ⅳ型功能反应的分数阶捕食者-食饵模型的动力学分析[J].井冈山大学学报:自然科学版,2019,40(3):9-13.

[8] Jin Z, Haque M.Global stability analysis of an eco-epidemiological model of thesalton sea[J]. J. Biological Systems,2006,14(3):373-385.

[9] Podlubny I. Fractional Differential Equations：An Introduction to Fractional Derivatives，Fractional Differential Equations，to Methods of their Solution and Some of their Applications[M].Academic press,1998.

[10] Matignon D.Stability result on fractional differential equations with applications to control processing[C]. IMACS-SMC proceedings,Lille,France,1996:963-968.

[11] Petras I. Fractional-order Nonlinear Systems：Modeling，Analysis and Simulation[M]. London，Beijing Springer：HEP,2011.

[12] Li Y, Chen Y. Podlubny I,Stability of fractional-order nonlinear dynamic systems：Lyapunov directmethod and generalized Mittag-Leffler stability[J]. Comput. Math. Appl,2010,59:1810-1821.

[13] Muhammed Çiçek, Yakar CoGkun, OLur Bülent. Stability,Boundedness，and Lagrange Stability of Fractional Differential Equations with Initial Time Difference[J].The Scientific WorldJournal，2014，Article ID 939027:1-7.

DYNAMICS OF A RATIO-DEPENDENT PREDATOR-PREY OF FRACTIONAL ORDER SYSTEM

*PU Wu-jun, DU Zheng-guang

(Department of Mathematics, Longnan Teachers College, Longnan, Gansu 742500, China)

In this paper, we studied the dynamic behavior of a fractional-order ratio-dependent predator–prey system with disease on the prey. The stability of all kinds of equilibrium points of the system was qualitatively analyzed with the linearization method, the sufficient conditions for the local asymptotic stability of the positive equilibrium point of the system were given, and the numerical simulation showed that the parameters and order of the system had an important influence on the convergence rate and stability of the equilibrium point.

fractional-order; ratio-dependent predator-prey model; local asymptotic stability; Hopf bifurcation

O157.13

A

10.3969/j.issn.1674-8085.2021.02.003

1674-8085(2021)02-0014-05

2020-10-14；

2020-12-04

陇南市2019年科技指导性计划项目（2019-ZD-14）

*蒲武军(1979-)，男，甘肃庄浪人，讲师，硕士，主要从事生物数学方面的研究(E-mail:puwj2005@163.com);

杜争光(1973-)，男，甘肃礼县人，副教授，主要从事应用微分方程方面的研究(E-mail:lnsz_dzg@163.com).