初中生数学高阶思维的结构模型①

周 莹 林 毅

(广西师范大学数学与统计学院 541004)

互联网技术的高速发展、全球化进程的持续发酵等时代因素推进了学生对高阶思维的需求，也促使高阶思维能力成为21世纪人才成功的先决条件.通俗来说，高阶思维是完成复杂任务、解决劣构问题的一种重要能力和心理特征，是21世纪的一种高级综合能力[1].数学作为中学教育中的主要科目，是一门极具抽象性、逻辑性的学科，核心素养的倡导要求数学课堂需要涵盖高阶思维的深度学习.通过高阶思维的参与，帮助学生超越灌输型的数学知识学习，深入挖掘数学知识的本质内涵，转向有意义构建的数学思维学习.然而，数学教育中大部分学生的思维层次处于低层次或中等层次，在数学学习中他们拘囿于定向思维、正向思维等单一思维方式思考问题，习惯于思维定势及循规蹈矩，拘囿于解决常规数学问题，却不善于解决复杂性、开放性的问题情境[2] [3] [4].就以“青浦实验”经验为例，研究组成员前后相隔17年对同为初中二年级的数千学生进行数学认知水平测试，测试显示，经历数学教学改革以来，学生的数学认知能力在前三个水平(操作性记忆水平、概念性记忆水平与说明性理解水平)都有显著提升，然而在最高水平——探究性理解水平并没有太多变化.此外，研究组成员还发现数学教师的课堂教学理念也明显从“重概念取向”转向“重概念兼顾能力取向”，强调高层次思维技巧和创造性思维技能成为数学课堂的主流思想.“青浦实验”虽是中国数学教育的一个缩影，其中折射出的问题却是国内数学教育者都应思考的，如何打破数学高阶思维发展的僵局？这也是生发本文研究灵感的启迪器，自认识到数学高阶思维的重要性及其匮乏困境，本文从探究初中生数学高阶思维的评价结构模型构建及测量两方面出发，以期深入认识数学高阶思维的内在结构机制，为数学高阶思维培养目标“落地”课堂教学提供参考与借鉴.

1 数学高阶思维结构的研究假设

为探究数学高阶思维的结构模型，本研究采用文献梳理及实证检验的混合研究范式，即从国内外数学高阶思维的相关研究成果中梳理其结构共性特征，结合我国数学教育特点提出数学高阶思维的结构模型假设，再佐以问卷调查形式验证其模型的合理性.

1.1 数学高阶思维的内涵

国内外学者对数学高阶思维的内涵认识多从其思维过程的角度出发.譬如，Klum(1990)提出，高阶数学思维过程包括所有不仅仅涉及记忆和模仿的信息活动，还包括信息的变化与重构，它具有复杂性、解法和应用标准不唯一等特点，另外整个思维过程还需耍思维者的自我监控，并设计一些详细的解释和判断过程[5]；David Tall认为高层次数学思维都应含有两个特征：思维对象包括严谨的数学定义，思维过程包含数学定理与命题的逻辑演绎，它在数学学习中表现为学习者对数学思维对象理解的透彻和精确性，并能按照数学的方法和规则进行合理严密的逻辑推理，具有较强的数学问题解决能力[6]；Sophocleous和Pitta-Pantazi(2015)基于整体化思维模型，认为数学高阶思维整合了基本数学知识、批判性思维、创造性思维和各种复杂的思维过程[7]；许礼光和沈琼认为高层次数学思维是一种综合性思维过程，常发生在元认知、问题解决、应用与创造性活动中，学生的思维经历联系与转化、抽象与扩展、批判与监控的过程[8].尽管学者们关注的数学高阶思维过程皆略有不同，但其中均有涉及共通的一般性高阶思维技能在数学学习领域中的表现，如问题解决能力、批判性思维、创造性思维及元认知能力.基于上述，本研究从思维过程方面阐述数学高阶思维的概念界定，即数学高阶思维是指在数学知识学习过程中，顺利运用批判性思维、创造性思维、问题解决及元认知能力为核心的高层次认知过程进行心智活动的综合性能力.

1.2 数学高阶思维的结构模型构建

综观数学高阶思维的本土化研究，学者们鲜少细致探究数学高阶思维的结构成分，多是以移植一般性高阶思维的结构框架或是单独研究数学高阶思维的某一特殊思维.譬如，张红霞、刘妍均以布卢姆认知目标分类学为基础，将分析、综合、评价和创造定为数学高阶思维[9] [10].在数学课堂教学中，培养学生的高阶思维能力是重要任务，也是课堂教学的重点问题[11].为方便教师在教学实践中展开对数学高阶思维的专项训练与培训，本文主要从数学高阶思维的主要子能力着手研究，以实现子能力的平衡发展推动数学高阶思维能力的整体提升.

就高阶思维能力要素的角度分析，研究者一般枚举高阶思维的主要分类，将复杂的高阶思维体系化为某几种认知能力的集合体，重点关注具体思维的认知过程.譬如，Lewis和 Smith(1993)提出，高阶思维包括批判性思维、问题解决、决策、创造性思维四种关键能力[12]； FJ King(1998)认为高阶思维能力是包括批判性思维、逻辑思维、反省思维、元认知和创造性思维的思维技能集合[13]；钟志贤教授(2004)认为高阶思维能力是指问题求解、决策、批判性思维和创造性思维能力[14]；黄国祯(2014)结合21世纪新时代对人才的要求，总结归纳出高阶思维的能力框架，包括：复杂问题解决能力和批判性思维能力、协作和沟通能力以及创造性思维能力[15].归纳以上国内外学者的研究成果，就如Udall与 Daniels(1991)所言，高阶思维至少包括三种思考，分别是批判思考、创造思考与问题解决[16].借鉴一般性高阶思维的结构共性，并突出在数学高阶思维过程中思维者的自我监控调节作用，本文以数学批判性思维、数学创造性思维、数学问题解决能力、数学元认知能力四条主线构建数学高阶思维的结构机制.问题是引发高阶思维过程的起点，因此，数学问题解决能力是高阶思维运转机制的基石，批判性思维和创造性思维作为两条主线贯穿在高阶思维认知过程中，而数学元认知能力作为上层建筑集中调控高阶思维的运行过程.

其中，数学批判性思维从属于批判性思维，引用李文婧的观点，数学批判性思维是指在数学学习活动中有目的、有意识地对已有的数学表述和数学思维过程、结果作出自我调节性分析、判断、推理、解释和调整的个性品质[17].通常，学者们会采用加利福尼亚批判性思维倾向测验(CCTDI)中对批判性思维的维度界定，即将批判性思维分为：寻找真相、开放思想、分析能力、系统化能力、批判性思维的自信心、求知欲和认知成熟度7个维度[18].数学创造性思维即指运用已有知识经验，在创造想象的参与下，通过思维揭示出数学对象的本质，而且在此基础上产生出某种新颖独特的、前所未有的思维成果的过程[19].考量数学创造性思维的能力水平一般从数学问题的多解法任务(Leikin，2009)着手，即以流畅性、灵活性和新颖性考察学生的数学创造性思维表现[20].数学问题解决能力是反馈学生数学能力的重要指标，蔡金法提出，数学问题解决是指学生将他们的数学知识综合应用于新的问题情境的能力，它要求学生能识别所遇到的问题，能判断这些问题的条件是否完备，并能根据已知条件构造和选择恰当的策略、综合所学知识去解决所碰到的问题，同时能对解题过程及答案作出评价，判断解题过程和答案的正确性[21].在此基础上，结合徐斌艳、高翔对数学问题解决能力的分析框架，本文将从策略合理性、表达清晰性及答案正确性三方面考察初中生的数学问题能力水平.数学元认知能力是指以数学认知活动、进程、结果等为对象的认知，也是学生对自己的数学认知活动进行计划、体验、监控和调节的过程[22] [23].为凸显数学元认知对数学认知活动的统筹功能，本文继承卡瓦诺和柏尔马特(Cavanaugh J C & Perlmutter M)的元认知结构三分法，将数学元认知能力分为数学元认知知识、数学元认知监控、数学元认知体验三个维度[24].基于上述，数学高阶思维的测量结构框架假设可呈现为“四维度十六因子”模型，如图1所示.

图1 数学高阶思维的测量结构框架假设

2 研究设计

2.1 问卷的初步编制

所编初始问卷的题目来源主要有：加利福尼亚批判性思维倾向测验量表(CCTDI)、姜玉莲的“高阶思维调查问卷”[25]、王光明团队的“初中生数学元认知调查问卷”[26].在问卷的编制初期，根据初中生数学学习特点及数学思考规律，对上述问卷进行引用及改编，随之结合广西师范大学的3名数学教育学专家与桂林中学的2名数学教师的指导意见，修改及增添部分题项，形成了65道题目的问卷初稿.问卷分为五部分，一为基本信息；二为数学批判性思维分量表28道题目；三为数学创造性思维分量表12道题目；四为数学元认知能力分量表14道题目；五为数学问题解决能力分量表11道题目.问卷采用李克特五点计分法，选项从“非常符合”、“符合”、“不确定”、“不符合”、“非常不符合”分别赋分为5、4、3、2、1.以问卷总分为数学高阶思维评价指标，分数越高表示数学高阶思维能力越强.

2.2 样本选取与调查过程

为了取样的代表性和普适性，调查样本分别从公立和民办两种学校属性的初中随机选取，其范围囊括了初一至初三三个年级.整个调查取样分为三个阶段进行.

第一阶段：预测.样本取自桂林市的广西师范大学附属外语实验中学、桂林市德智中学，共发放问卷304份，经剔除问卷答案呈规律性、统一性、多选性以及大部分未作答的无效问卷，得到有效问卷270份，问卷有效率为88.82%.其中初一94人，初二98人，初三78人，男女比例为1∶1.177.该部分有效问卷数据经使用SPSS软件进行项目分析及探索性因子分析，剔除部分问卷题项，检验数学高阶思维的测量结构框架假设，以形成再测问卷.

第二阶段：再测.样本取自桂林市的广西师范大学附属外语实验中学、桂林中学、宝贤中学.共发放问卷987份，经剔除无效问卷，得到有效问卷910份，问卷有效率为92.20%.其中初一465人，初二301人，初三144人，男女比例为1：1.106.该部分有效问卷数据主要进行信效度分析，经验证性因素分析及相关性检验来考察问卷的结构效度，以学业成绩为校标考察问卷的校标效度，并以Cronbach α系数与分半信度同时表征问卷信度，进一步明确数学高阶思维的测量结构框架，形成正式问卷.

第三阶段：重测.该阶段以正式问卷调查再测调查的部分学生.其中回收问卷160份，经剔除无效问卷，得到有效问卷143份，问卷有效率为89.4%.该部分有效问卷数据主要用以计算重测的Cronbach α系数以验证问卷是否具有良好的稳定性.

3 问卷的预研究结果分析

3.1 项目分析

项目分析的主要目的在于检验编制的量表或测验个别题项的适切性或可靠程度，其过程就是探究高低分的受试者在每个题项的差异或进行题项间同质性检验，其结果可作为个别题项筛选或修改的依据[27].本研究采取的项目分析手段分别是极端组比较法和同质性检验法.首先，将问卷中的反向题进行反向计分，并重新核验输入数据有无缺失值或是错误值.随之，求出量表个别题项的临界比值(critical ratio 简称 CR 值)，即以根据题项总分加以排序分为高分组(总分最高的27%)和低分组(总分最低的27%)两组，对两组进行独立样本T检验，删除高低分组平均数差异检验未达0.05显著水平且CR值小于3.000的题项，共2道(27、28).而后，求出题项总分与个别题项的相关系数矩阵，剔除显著性(双尾)p的数值大于0.05且相关系数小于0.3的题项，共6道(3、4、6、7、27、28).综合项目分析情况，问卷题项由65道精简到59道.

3.2 探索性因素分析

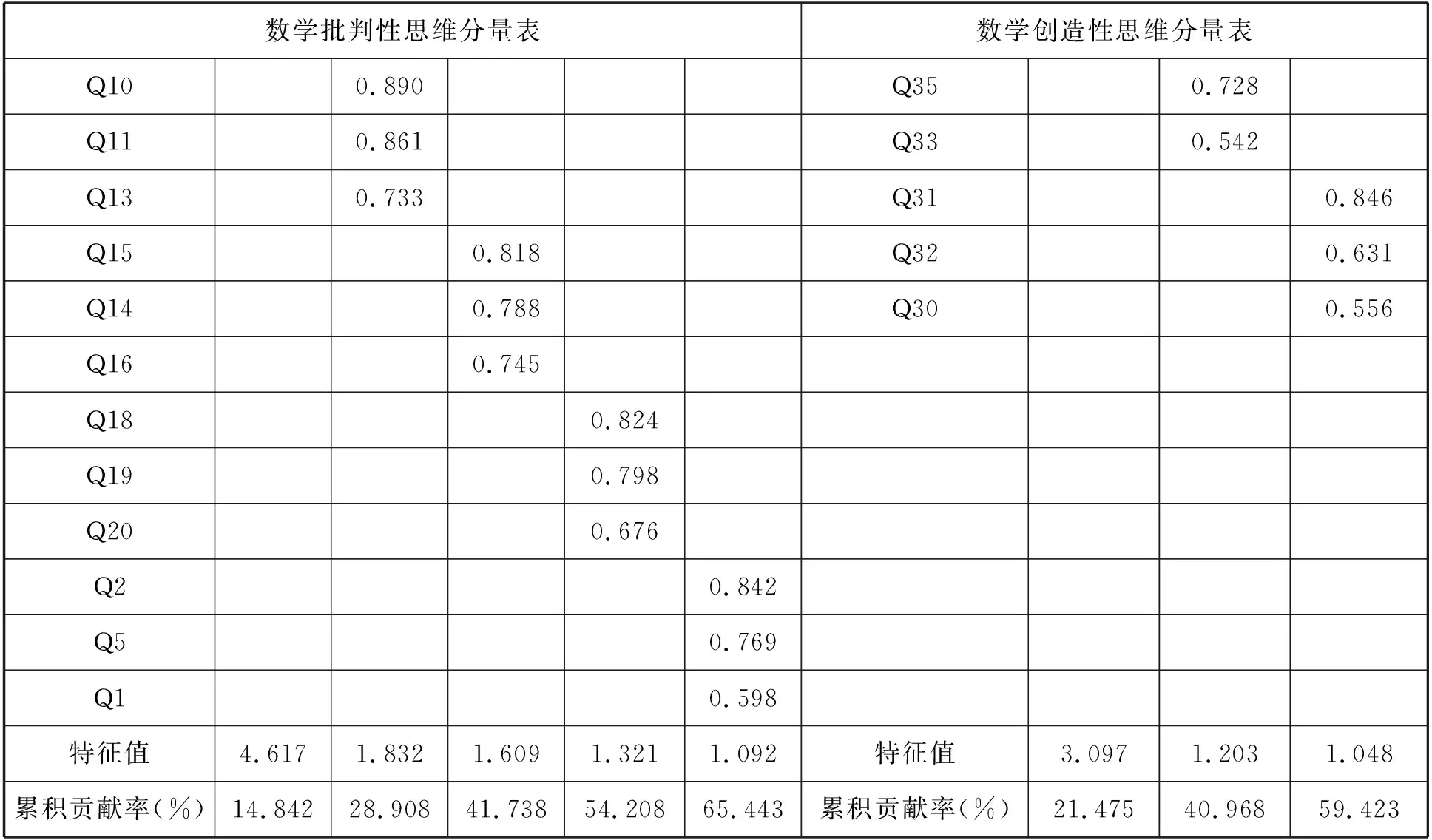
进行探索性因素分析的目的在于侦测量表的潜在结构，检验数学高阶思维的测量结构假设是否合理，同时进一步缩减题项的数目.首先就理论结构四个主维度分别计算其KMO抽样适当性参数与Bartlett’s的球形检验，根据Kaiser(1974)的评判标准，四个主维度的KMO值均在0.7上下区间，且χ2值显著(p=0.000<0.05).KMO与Bartlett’s检验结果表明，四个分量表的KMO值在0.689至0.818之间，且χ2值显著，表示问卷数据具有共同因素存在，适合于进行因素分析.紧接着，采取主成分分析法及最大方差旋转法确定四个主维度的因素结构及各因素所含的题项数目，共同因素保留的判断依据为因子数符合碎石图检验、因素特征值大于1且至少包含3道题项、题项因素负荷大于0.5以及共同性大于0.2.根据上述原则对数据进行探索性因素分析，可剔除15道题项(8、9、12、17、25、26、29、36、40、44、48、49、50、54)，形成44道题项的再测问卷，探索性因素分析结果如表1-2所示.

在探索性分析过程中，由于数学批判性思维分量表的原假设开放思想与认知成熟度维度中仅含2道题项，不满足共同因素保留原则，因此剔除这两维度.经探索性因素分析可见，各分量表所萃取的公共因子累积解释方差占总方差的百分比分别为65.443%、59.423%、52.422%、57.988%，均在50%以上，满足方差百分比决定法的最低要求，说明所萃取的公共因素基本可以反映数学高阶思维的潜在特质.综合问卷四个主维度的探索性因素分析结果及问卷的理论构念，数学批判性思维分量表(共16项)的五个因素分别命名为：求知欲、分析能力、系统化能力、批判性思维的自信心、寻找真相；数学创造性思维分量表(共9项)的三个因素分别命名为：新颖性、灵活性、流畅性；数学元认知能力分量表(共9项)的三个因素分别命名为：元认知知识、元认知体验、元认知监控；数学问题解决能力(共10项)的三个因素分别命名为：答案正确性、策略合理性、表达清晰性.因此，除了数学批判性思维的维度架构与假设有所出入，其他分量表的维度架构均与假设一致.

表1 数学批判性思维分量表与数学创造性思维分量表的探索性因素分析结果

续表

表2 数学元认知能力分量表与数学问题解决能力分量表的探索性因素分析结果

4 问卷的正式确定及结果分析

根据再测样本(n=910)的有效问卷数据，再次使用极端组比较法和同质性检验法进行分析，结果显示高低分组平均数差异检验均达0.05显著水平且CR值大于3.000，题项与总分的相关系数均大于0.3，因此，无需进一步剔除问卷题项.同时，对再测样本数据进行探索性因素分析，分析结果与预测样本数据的问卷结构架构基本吻合，说明问卷因素确定合理.

4.1 结构效度分析

4.1.1 验证性因素分析

为进一步探究数学高阶思维问卷的因素结构模型是否与实际搜集的数据契合，以及指标变量是否可以有效作为问卷因素构念(潜在变量)的测量变量，利用AMOS 20.0软件对再测样本数据进行验证性因素分析，其中，运用最大似然估计法(Maximum Likelihood)进行模型运算.根据相关文献研究和探索性因素分析的结果建构，待验证的因素结构模型有：模型一、数学批判性思维分量表的结构模型；模型二、数学创造性思维分量表的结构模型；模型三、数学元认知能力分量表的结构模型；模型四、数学问题解决能力思维分量表的结构模型；模型五、数学高阶思维总问卷的结构模型.由表3所呈现的整体模型拟合情况检验结果来看，绝对适配度指数、增值适配度指数、简约适配度指数均达模型可接受的标准，表示本研究所提的理论模型与实际数据是可以契合的，即模型一至模型五的外在质量佳，结构效度良好.初中生数学高阶思维的整体测量结构模型由图2所示，各测量项目在其所属共同因素上的因素负荷量均在0.60-0.76之间，说明问卷结构清晰，本文的问卷结构模型设置较为合理.

表3 数学高阶思维问卷验证性因素分析的拟合指标

图2 初中生数学高阶思维的测量结构模型

4.1.2 相关性检验分析

除了验证性因素分析，相关性检验分析也是问卷结构效度检验的一个常用方式，即通过SPSS软件计算并比较问卷各主维度之间的相关系数及其与总问卷的相关系数.计算结果见表4，问卷各主维度的相关系数在0.392～0.572之间，处于中等程度的相关水平，而各主维度与总问卷的相关系数在0.710～0.889，相关水平呈现良好态势.这说明问卷各主维度之间既相互联系，也具备良好的独立性，能客观反映问卷所需测量的内容.

表4 数学高阶思维问卷的相关性检验结果

4.2 校标效度分析

本研究采用高分组和低分组学生的数学高阶思维差异分析作为数学高阶思维问卷的预测效标.按100分制，通常以60分为及格线，则将学生的最近一次集体测验的学业成绩作为分组依据，高于60分记为高分组，反之为低分组.由独立样本T检验结果显示，高分组学生在数学高阶思维各因素得分及总分均高于低分组学生，且显著性概率值P均小于0.05，这说明高低分组学生在数学高阶思维及其各因素水平均在统计学上呈现显著性差异；同时，由实际效果值Eta Squared统计结果可见，效果值均大于0.14，即表示学业成绩与数学高阶思维及其各维度在实际上呈现一种高度关联强度.基于上述，数学高阶思维问卷具有较高的校标关联效度.经结构效度分析及校标效度检验可得结论，44道题项的再测问卷效度良好，可作为初中生数学高阶思维测量的正式问卷施以调查.

表5 高低分组学生的数学高阶思维差异分析

4.3 信度分析

所谓信度，指的是测验工具所得结果的可靠性与稳定性.本研究对再测样本数据(n=910)进行统计得出总问卷及各分量表的Cronbachα系数，同时就总问卷按奇数题或偶数题分割成两个次量表，计算其折半信度，以检验问卷的内在信度；再而就重测样本数据(n=143)进行统计得出重测信度，以检验问卷的外在信度.统计结果表明，总问卷的Cronbachα系数为0.924，分量表的Cronbachα系数在0.757～0.875之间，总问卷的折半信度为0.832，分量表的折半信度在0.668～0.815之间，由此可见，总问卷及分量表的内部一致性较高.在重测中，总问卷的重测信度达0.920，各分量表的重测信度0.750～0.837之间，说明测量问卷的稳定性较好，外在信度达标.

5 讨论及结论

5.1 数学高阶思维的结构

数学高阶思维的测量是数学高阶思维实证研究的重要组成部分，对客观把握数学高阶思维水平，深入探究数学高阶思维的影响机制以及长远性探索其培养策略具有重要意义.然而，现有数学高阶思维的相关研究并不多，更缺乏科学高效的测量问卷对数学高阶思维水平进行大规模的测评研究.在国内学者的认知中，数学高阶思维应是多维结构的思维体系，然而由于研究者对其概念内涵理解、研究视角的不同，往往生发出不同的数学高阶思维结构模型.譬如，周超的五维数学高阶思维模型(深刻性、灵活性、独造性、批判性与敏捷性)[28]、张红霞的四阶层数学高阶思维模型(分析、综合、评价和创造).本章基于已有研究经验，以通用高阶思维的共有能力要素为基础，结合数学学科特征明确界定了数学高阶思维：数学高阶思维是指在数学知识学习过程中，顺利运用批判性思维、创造性思维、问题解决及元认知能力为核心的高层次认知过程进行心智活动的综合性能力.在其概念基础，深入探寻其主要能力要素的测评经验，形成测评模型构想，并依据初中生思维发展规律，征求有关专家意见编制对应的问卷工具.为验证该理论构想，研究以1000多名初中生学生分批展开问卷的预测、再测及重测，并就有效问卷数据进行探索性分析和验证性分析.结果显示，除了数学批判性思维的维度架构与理想构想有所出入，其他分量表的维度架构均与理论构想一致.分析数学批判性思维中开放思想及认知成熟度的缺失原因，可归结于通用性批判性思维移植数学学科的不适性，这两因素更指向一般性批判思维特征，数学学科特征在其中表现不够明显.总的来说，研究中的数学高阶思维结构构想还是得到了大量实证数据的有力支持，因此，数学高阶思维以数学批判性思维、数学创造性思维、数学元认知能力及数学问题解决能力为要素进行测评的想法是合理的.

5.2 数学高阶思维的心理测量学特征

研究通过系统梳理国内外高阶思维、数学高阶思维等相关文献，明确提出数学高阶思维的操作性定义及测评模型构想.在问卷初稿编制过程中，研究者邀请了数名数学教育学及心理学专家、一线数学教师对问卷条目进行修订，并挑选数名初中生对问卷条目的可读性进行验证，综合各方反馈意见再次确定问卷初稿条目65项，以确保问卷的内容效度.为确保问卷条目质量，研究进行了三轮不同规模的测试及测量学分析.首先以预测检查问卷结构，经极端组比较法和同质性检验法进行项目分析剔除6道低效题项，并经探索性分析剔除了15道题项，形成了四维度十四因子的测评模型，各维度的累积贡献率均达50%以上，合理验证及修正了原问卷结构的模型假设.而后以再测检验问卷质量，经验证性因素分析及相关性检验测评问卷的结构效度，并以学业成绩为校标检验其校标效度，结果显示，双重效度分析结果均呈现良好状态，说明问卷结构设置合理且有效.最后辅以重测验证问卷可靠性，同质性信度、分半信度及重测信度测试结果表明问卷具有良好的稳定性，内外在信度均达标.基于上述，初中生数学高阶思维问卷的各项效度指标、信度指标均达到心理测量学标准，可见，该问卷是一个可靠、有效的心理学测量工具.