神坛上的达·芬奇(续)——以达芬奇的数学手稿为中心

代 钦

(内蒙古师范大学科学技术史研究院 010022)

5 达·芬奇的数学证明及其启迪作用

发现问题、解决问题和证明命题是数学研究的重要内容，其中蕴含着直觉(直观)想象能力和理性精神.数学命题的证明要言必有据，简洁清晰.达·芬奇缺乏数学证明的严格训练，原因有以下几个方面：首先，达·芬奇没有接受系统的数学教育，16岁之前只接受过几个月的数学教育，在遇到卢卡·帕乔利之后才开始向他学习数学.这说明达·芬奇大部分数学知识是自学的，不成系统.另外，在达·芬奇手稿中的几何图形、工程建筑图形数量压倒性得多，这就导致人们错误地认为达·芬奇只注重直观想象而忽略了抽象的演绎证明.其次，从1473年(21岁)开始，达·芬奇采用了从右至左的“镜像”书写方法，读者直接阅读他的文稿是非常困难的，必须通过镜像才能正常阅读.他使用“镜像”书写方法的目的在于防止他的研究成果被剽窃.因为那个年代还没有可以让人宣布发明权的期刊，也没有专利申请或保护发明者不受剽窃侵害的机构.再次，达·芬奇的行文表达给别人的印象也很一般，正如欧仁·明茨所说：“对于当时的人文主义学者来说，精确清晰的语言表达是驾轻就熟的本领，而未曾受过修辞学教育的列奥纳多，则习惯于用一套自己熟悉的方式来记录他的研究成果.也许，他孤僻的性格与非凡的创造能力存在着一定的联系，正如所谓的‘自古天才皆寂寞’.他的论述科学的文风既不出彩，也不简洁.他的想法缺乏当时文人学者的系统性和条理性.他没有把公式和想法整理成一个“理论体系”，而是把他的发现组织成段落，平铺直叙，丝毫不带学究气或哲学条理.”(1)欧仁·明茨.列奥纳多·达·芬奇(第二卷)[M].陈立勤，译.北京：人民美术出版社，2014：54.最后，达·芬奇的认知与实践之间的矛盾是明显的.“优柔寡断是他性格中的主导因素.随着研究范围的扩展，这种性格便愈趋明显，使他难以在一个方向长时间地集中精力，无法归纳出有力而权威的结论.”(2)欧仁·明茨.列奥纳多·达·芬奇(第二卷)[M].陈立勤，译.北京：人民美术出版社，2014：60.在他的数学手稿中经常看到这种现象.尽管如此，我们在达·芬奇手稿和笔记中也常常看到注重逻辑证明的理性精神和对一些复杂的数学命题的证明.如他提醒自己“大胆怀疑，小心求证.”(3)[意大利]达·芬奇.达·芬奇艺术与生活随笔[M].戴专，译.北京：光明日报出版社，2012：129.他也认为“在伟大的数学事实里，论证的确定性最为显著地提升了研究者的思维能力.”(4)[意大利]达·芬奇.达·芬奇艺术与生活随笔[M].戴专，译.北京：光明日报出版社，2012：97.而且他格外看重数学的论证，他认为：“人类的任何研究若不经数学的论证就不能称为真科学.”(5)[英]艾玛·阿·里斯特.达·芬奇笔记[M].郑福浩，译.北京：生活·读书·新知三联书店，2007:6.达·芬奇也对数学论证中的由因推果、由果索因等方法提出了独到的见解.

下面主要介绍三个问题：1.达·芬奇对勾股定理及其证明的热衷；2.对“化圆为方”的痴迷与希波克拉底定理的广泛应用——直线形与曲线形的等积变换；3.立体几何命题的证明.

5.1 达·芬奇对勾股定理的研究

勾股定理，正如开普勒所说是数学中的黄金.有了勾股定理才会发现无理数，以至产生连续的概念、函数的概念；有了勾股定理才会计算两点间的距离，从而为笛卡儿创立解析几何奠定了基础.这些数学成就直接促使了微积分乃至现代数学的诞生.正因为如此，自古以来勾股定理吸引了成千上万的数学爱好者和数学家，出现了勾股定理的数百种证明方法.数学发展史上没有第二个定理有如此丰富的证明方法.在历史的长河中，作为文艺复兴时期伟大的艺术家和科学家的达·芬奇对勾股定理情有独钟，不仅给出了一种别出心裁的证明，而且其手稿中能够见到勾股定理的直观表达的各种图形有一百多处.

达·芬奇各种手稿提供了一个重要信息，即他系统地学习了欧几里得《几何原本》，并对勾股定理等内容有自己的见解或扩展性思路.他在欧几里得证明方法的基础上，给出一个证明方法，具体如下(6)E.S.Loomis. The Pythagorean Proposition[M].Washington: National Council of Teachers of Mathematics，1972年复刻版.：

如图17，Rt△AEK中，已知∠AKE=90°，KE=a，AK=b，AE=c，求证:AK2+KE2=AE2.

图17 达·芬奇的勾股定理证明

证明：分别以AK、KE、AE为边作正方形AKHI、KEFG、ABDE.以正方形ABDE对角线交点为中心，将△AKE旋转180°至△DCB.连接线段CK、IF、HG.△AKE与ΔHKG关于线段IF对称，所以S△AKE=S△HKG，且I、K、F三点共线.

∠IAE=90°+∠α=∠KAB，∠ABC=90°+∠β=∠AEF，四边形IAEF可理解为关于点A逆时针旋转90°，所以四边形KABC与四边形IAEF全等，即S四边形ABCK=S四边形IAEF，且有

S正方形ABDE+2S△AEK

=S六边形ABCDEK=2S四边形ABCK

=2S四边形IAEF=S六边形AEFGHI

=S正方形AKHI+S正方形KEFG+2S△AKE，

于是有S正方形ABDE=S正方形AKHI+S正方形KEFG，

也即AK2+KE2=AE2或a2+b2=c2.

达·芬奇对勾股定理情之所钟，在他手稿中经常见到勾股定理的欧几里得证明方法之图形及由此而引发的各种有趣的变形问题(在直角三角形两个直角边上向外作两个正方形，斜边上向内作一个正方形)和其他扩展性问题.

达·芬奇给出了勾股定理的上述证明的同时，也思考了另外一种情形，在直角三角形两个直角边上向外作正方形，在斜边上向内作正方形，如图18(7)达·芬奇.大西洋古抄本[M].第1353页.左下角和右上角两幅图所示.

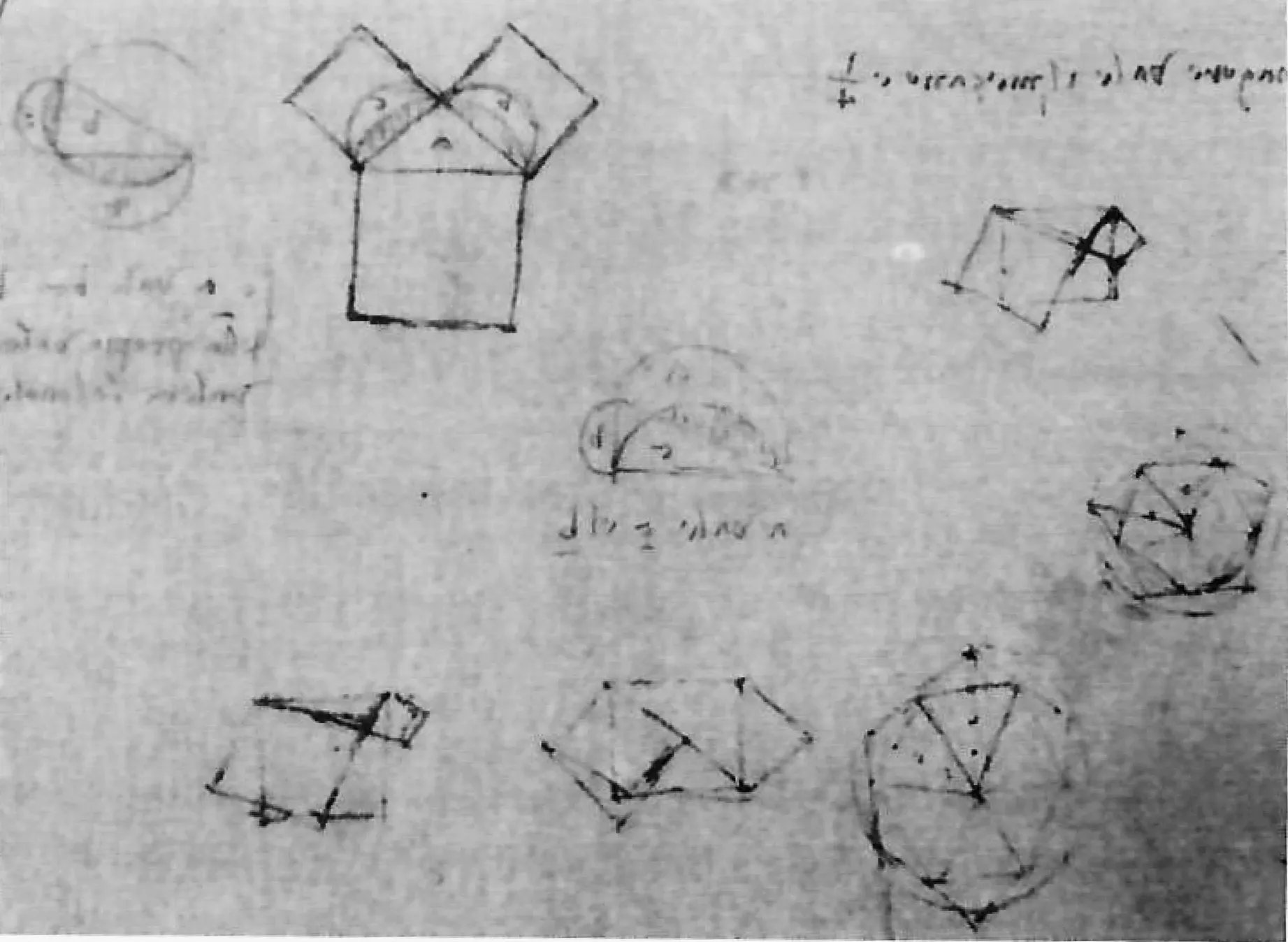
图18

达·芬奇虽然没有给出证明过程，但是该图形从直观上给人一种有益的启示.根据这个图形也很容易证明勾股定理，如图19.

图19 勾股定理证明

我们可以根据图18中勾股定理图形证明该定理，具体如下：

如图19所示，在Rt△ABC中，已知∠A=90°，求证:BC2=AB2+AC2.

证明：分别以AC、AB、BC为边作正方形ACDE、ABFG、BCHI.延长边DE和边FG并交于点M.

有S矩形BNLI=S平行四边形MIBA=S正方形ABFG，

同理有S矩形HLNC=S平行四边形HCAM=S正方形ACDE.

因为S正方形BCHI=S矩形HLNC+S矩形BNLI，

所以S正方形BCHI=S正方形ACDE+S正方形ABFG，

即BC2=AB2+AC2.

(2)勾股定理的扩展性思考

①在不破坏直线形的情形下，直角三角形三个边上的正方形内切圆面积是否有与勾股定理相当的结果，如图20.

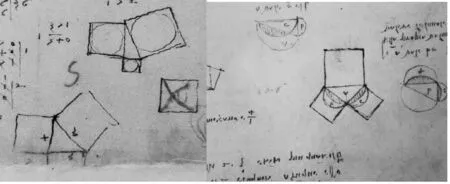
图20 达·芬奇对勾股定理的扩展性思考1

图21 达·芬奇对勾股定理的扩展性思考2

②在直角三角形中，分别以三边为直径的半圆面积是否有与勾股定理相当的结果.

③在曲线形直角三角形三边上作弯曲的正方形(弯曲菱形)并思考能否有与勾股定理相当的结果.如图21(8)达·芬奇.大西洋古抄本[M].第1337页.，曲线形直角三角形勾股命题的直观图形，这一想法本身就有很高的科学思想方法的价值.达·芬奇认为有三种曲线形三角形：(1)两边为直线一边为曲线的三角形；(2)一边为直线两边为曲线的三角形；(3)三边皆为曲线的三角形.无论是哪一种曲线三角形，都会让人思考一个问题，那就是曲线三角形的内角和是否是180°以及三角形的哪些性质仍然保持不变.于是很容易产生拓扑学的观念了.甚至有人认为“列奥纳多也是拓扑学领域的开拓者”.(9)[美]沃尔特·艾萨克森.列奥纳多·达·芬奇——从凡人到天才的创造力密码[M].汪冰，译.北京：中信出版社，2018:208.

④如果将直角三角形三边上的正方形扩展为立方体(或长方体)，如图22(10)达·芬奇.大西洋古抄本[M].第1383页.，那么以斜边为边的立方体体积是否等于分别以两条直角边为边的立方体的体积之和？(设直角三角形斜边为c,两个直角边分别为a、b，那么c3=a3+b3？).我们不妨把这个命题称为“立方体的勾股命题”.这实际上是倍立方体问题的一般情形.达·芬奇虽然没有给出自己的结论，但是从他的手稿中多处出现的类似几何图形可以看出，达·芬奇至少从勾股定理的结论类比得出一些有趣的问题.这些问题具有很高的数学思维方法方面的价值.

图22 立方体的勾股命题

5.2 达·芬奇对希波克拉底定理的应用

古希腊人提出了三大作图问题：三等分任意角；倍立方体，求作一立方体，使其体积为已知立方体体积的两倍；化圆为方，求作一个正方形，使其面积等于已知圆的面积.这三大作图问题有只使用没有刻度的直尺和圆规之限定条件.数学史上已经证明了在限制条件下不能解决三大问题.但是在这一过程中不知多少学者殚精竭虑地探险并开辟新的道路，在这曲折而漫长的路上达·芬奇也留下了自己的足印.倍立方体问题和化圆为方问题引起了达·芬奇的浓厚兴趣，特别是化圆为方问题使他痴迷到疯狂的程度，甚至他宣布已经解决了该问题：“在圣安德助日(11月30日)，我来到化圆为方的终点；在晚间烛光即将熄灭时，在我写的纸张上‘完成’了.”(11)华特·艾萨克森.达文西传[M].严丽娟，林玉菁，译.台北：商周出版，2019:220.

图23 471v几何游戏

除此之外，达·芬奇的兴趣更倾向于曲线型和直线形之间的等积问题，由此引出各种月牙形图案.月牙形是一种边缘为两个圆弧的平面图形.这主要体现在他的很多工程设计、建筑设计和几何学手稿中.特别是在“几何游戏”中给出的36幅图形更是令人叹为观止，如图23.“471v几何游戏”的主题就是由圆和正方形的各种内切、外接、重叠、交叉等具有创意的操作而形成的各种图案.其中，有一半以上图形中有月牙形.据说，达·芬奇在试图解决“化圆为方”问题的过程中，废寝忘食地制作了各种各样的月牙形、曲线三角形等有规则的图形.他把制作月牙形的过程看作一种智力游戏，因此“决定写一本论文——取名为《几何学游戏》——想法填满了一页又一页.可想而知，这本书也加入了其他未完稿的论文行列.”所谓“论文行列”就是《大西洋古抄本》.达·芬奇玩月牙形玩得快疯了，就像月亮会影响人的情绪，引发精神失常(12)华特·艾萨克森.达文西传[M].严丽娟，林玉菁，译.台北：商周出版，2019:219..

达·芬奇的月牙形问题来自古希腊数学家和天文学家希波克拉底(Hippocrates of Chios, 公元前5世纪下半叶).他生于希俄斯，公元前5世纪下半叶活动于雅典.早年经商，不幸落入海盗之手，财产丧失殆尽.为诉讼和查访，在雅典住了很长时间，其间常到学校听课.后来从事几何学研究，做出杰出贡献.他在研究化圆为方问题时提出一种化月牙形为方形的方法，并将一个月牙形和一个圆一起转化为正方形，认为这样就可以化圆为方.结论虽然有误，但在解决这一问题过程中使用的方法和显示出的几何技巧长期为人称道.希波克拉底的月牙形问题有以下三种不同情形：

(1)在直角三角形ABC中，如果以两直角边AC、BC为直径向形外作半圆，又以AB为直径向形内作半圆，则S月牙形AC+S月牙形BC=S△ABC，如图24(13)沈康身.历史数学命题欣赏[M].上海：上海教育出版社，2002:633..

图24 希波克拉底定理1

(2)设扇形AOC为一个圆的四分之一.以AC为直径在这四分之一圆的外面，作一个半圆.试证明：以这四分之一圆和这个半圆所围的月牙形，与△AOC面积相等，如图25.

图25 希波克拉底定理2

(3)设ABCD等于以AD为直径的圆的内接正六边形的一半.作该圆与以AB为直径的半圆之间的月牙形.试证明：梯形ABCD的面积等于该月牙形面积的三倍加上以AB为直径的半圆的面积，如图26.

图26 希波克拉底定理3

5.3 立体几何证明

立体图形体积问题的研究内容主要在《马德里手稿Ⅱ》第44页-47页、第65页-70页.达·芬奇其他手稿中也有一些研究立体体积的内容.下面从《马德里手稿Ⅱ》中摭取三棱锥与正方体体积关系研究的一幅手稿，举例说明，如图27(14)Leonardo Da Vinci. Tratados Varios De Fortificacion Estatica Y Geometria Escritos En Italiano Ⅱ：Library Number 8936[M].Tokyo: Iwanamisyoten, 1975：70.，是将正方体分割成6个体积相等的三棱锥的过程，并给了简单证明.

图27 立体体积研究

把达·芬奇用镜像写法写的论证过程反过来观看，并翻译成现代形式，如图28-34，具体如下：

V三棱锥d-cbg=V三棱锥f-cbg(c-bfg)=V三棱锥n-bfg，

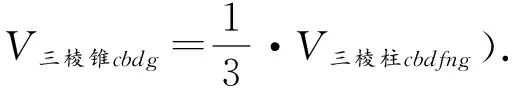
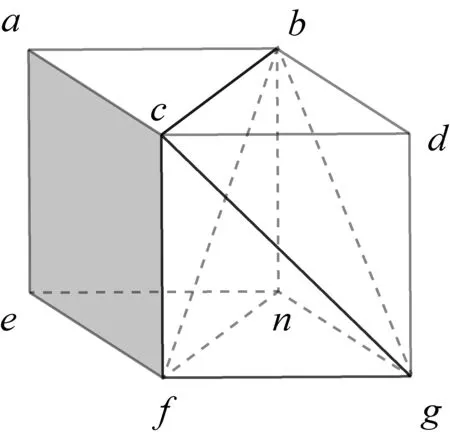
图28

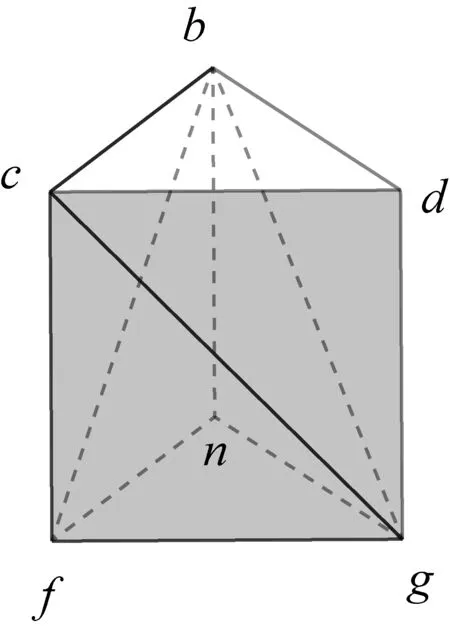
图29

图30

图31

图32

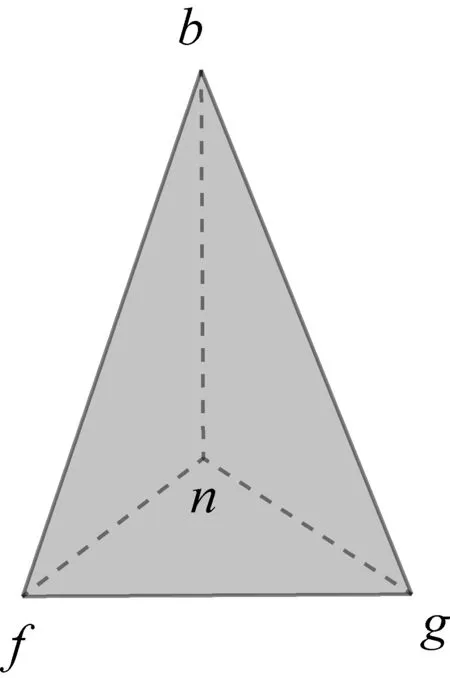
图33

达·芬奇这个证明过程的整体思路和步骤是正确的，但是在个别细节问题上犯了写错字母的错误，我们在这里根据他的证明的说明予以纠正.

6 立体图形的制作

用数学家的眼光看多面体的几何图形，就是由点线面组成的抽象的一个存在，换言之，这些几何图形与现实世界的具体事物无关.但是在达·芬奇的精神世界里多面体具有反映生命和自然相互统一的意义.在研究炼金术的过程中，达·芬奇发现可以人为地合成自然界中所没有的化合物，他由此想到，利用几何设计同样可以创造出大自然中不存在的形体，也许可以揭示大自然隐秘不为人知的一面.另一方面，达·芬奇认为，人是微缩的地球，……因为人也是由土、水、气和火构成，构成地球的要素也是构成人的要素(17)[意大利]达·芬奇.达·芬奇艺术与生活笔记[M].戴专，译.北京：光明日报出版社，2012:149..达·芬奇的这一观点是古希腊哲学家毕达哥拉斯和柏拉图关于宇宙万物形成元素的哲学观点的继承.即他们认为，正多面体有五种，它们对应宇宙元素情况如下：土元素对应正六面体，火元素对应正四面体，水元素对应正二十面体，气元素对应正八面体，而正十二面体则象征着浩瀚的天空.宇宙万物用这种几何语言书写了它的结构和规律.达·芬奇以柏拉图的五种正多面体为出发点，在结合数学与艺术的内在联系的基础上，创作了精妙绝伦的多面体图形，让人们领略到数学的纯粹美和达·芬奇的惊世才华.

达·芬奇手稿中的图形多为立体图形，其中为其老师卢卡·帕乔利著作《神圣比例》(如图34)而作的插图是最著名的.1496年达·芬奇与卢卡·帕乔利一同被聘请到米兰宫廷后，达·芬奇有了向卢卡·帕乔利学习数学的良机，这使达·芬奇的数学水平有了很大的提高.1498年，达·芬奇为卢卡·帕乔利的著作《神圣比例》以柏拉图五种正多面体为中心画了60幅插图，其中1幅为教堂门，3幅分别为圆柱体、圆锥体和球，其余为28种多面体的开窗型和具体型成对出现的56幅图，如图35.这些图形的制作充分展示了达·芬奇卓荦不羁的空间直观想象能力.在历史上有人已经画过柏拉图正多面体，但是，“达·芬奇针对它们设计了一种更‘具体的’展现方式.他用钢笔、墨水和水彩将这些形状画成悬挂在空间中、光影中以对称方式塑造的实物.如图37、图38.此外，他还将每个形状绘制成‘开窗’的式，以便向人们全面展示每个形状的空间组合情况.”(18)[英]马丁·肯普.达·芬奇100个里程碑[M].叶芙蓉，译.北京：金盾出版社，2019:83.

图34 帕乔利《神圣比例》封面

De divina Proportione(《神圣比例》，1498年)(19)Luca Pacioli. De divina Proportione [M].XXI-XXII中立体图形的制作耗费了达·芬奇的大量心血，有些图形的制作过程在其手稿的不同地方能够见到，如在《大西洋古抄本》中制作空心正二十面体时，先作了一个简单的素描(如图36)，然后作了完整的图36(20)达·芬奇.大西洋古抄本[M].第518r，第1203页..

图35 《神圣比例》中正十二面体

图36 518r“几何学研究”

图37 达·芬奇为《神圣比例》作的插图

图38 达·芬奇为《神圣比例》作的插图

除上述几何图形外，在达·芬奇手稿中还有一些富有启发性的几何图形，如图39“三维透视研究”(21)达·芬奇.大西洋古抄本[M].709r，第893页..我们用三张大小相同的正方形纸张可以制作该图的模型，连接各顶点就得到一个有规则的二十面体，但不是正二十面体.既然用三个相同的正方形两两垂直地交叉后得到一个有规则的二十面体，那么使用类似方法适当改变几何图形形状能否得到一个正二十面体呢？答案是肯定的.我们可以用三张大小相同的黄金矩形制作该模型.

图39 709r三维透视研究

人们由“三维透视研究”联想到用三张相同的黄金矩形能够制作正二十面体的过程是富有创意的.这种方法在中小学数学教学中有重要的用武之地，通过类似的活动可以培养学生手脑并用的能力，同时能够增进学生数学文化知识，也可以培养学生对数学的学习兴趣.

图40 黄金矩形

图41 正二十面体的制作

图42 正二十面体

7 达·芬奇的数学应用

达·芬奇的数学应用涉及到他研究的所有领域，是极其广泛的.这里仅简要地介绍他在绘画创作中的数学应用——比例理论和透视法.达·芬奇在不少绘画创作中用到了数学，这是肯定的，如《维特鲁威人》《马的研究》等.在有些作品的创作中并不一定用到数学，他通过直觉可以把握要创作的诸对象的位置和大致比例，如不少人认为达·芬奇《最后的晚餐》《蒙娜丽莎》的创作中严格地使用了透视法、黄金比例，尽管在他的相关手稿中没有发现使用透视法的迹象,“但是这依然无法令人信服地证明列奥纳多在创作中自觉使用了精确的数学比例.”(22)[美]沃尔特·艾萨克森.列奥纳多·达·芬奇——从凡人到天才的创造力密码[M].北京：中信出版社，2018:207.

7.1 维特鲁威人

马尔库斯·维特鲁威·波利奥(Marcus Vitruvius Pollio)，公元前1世纪生活于罗马共和制向帝制过渡的重要转折时期，他是一个“保守主义者”，不遗余力地维护从古希腊传承下来的人文价值观和建筑理想.他学习研究的领域包括绘图、几何学、算术、光学、历史学、哲学、音乐学、医学、法律、天文学、古典语文学、古典文献学等，非常广泛.我们从他的经典著作《建筑十书》中可以看到这些研究领域.由于文艺复兴时期的人文主义者崇尚古代文学艺术的辉煌，对希腊语和拉丁语文献抱有浓厚的兴趣，这使维特鲁威的《建筑十书》进入他们的视野.因此，维特鲁威的《建筑十书》很自然地成为了达·芬奇学习研究的珍贵文献，并对他产生了深刻影响.也许是一种巧合，维特鲁威有“措辞笨拙，语句臃肿，忽然节外生枝”(23)[古罗马]维特鲁威.建筑十书(典藏版)[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注；陈平，中译.北京：北京大学出版社，2019:英译者前言XIII.的写作方式，而达·芬奇在这方面有过之而无不及，甚至在一张稿纸上写完全不同的内容，而且还采用镜像书写方法.

图43 人体比例

《建筑十书》第3书中有：一座建筑应反映出人体的比例.维特鲁威认为大自然是按照下述方式构造人体的，面部从颏到额顶和发际为身高的十分之一，手掌从腕到中指尖也是如此；头部从颏到头顶为八分之一；从胸部顶端带发际包括颈部下端为六分之一；从胸部的中部到头顶为四分之一.面部本身，颏底至鼻子最下端是整个脸高的三分之一，从鼻下端至双眉之间的中点是另一个三分之一，从这一点至额头发际也是三分之一.脚长是身高的六分之一，前臂为四分之一，胸部也是四分之一，其他肢体又有各自相应的比例.

图44 维特鲁威人

这种人体比例的思想对达·芬奇的绘画创作也产生了重要影响.达·芬奇也崇尚维特鲁威的人体比例并强调运用维特鲁威的比例，指出建筑师维特鲁威把人体的尺寸安排如下：四指为一掌，四掌为一足，六掌为一腕尺，四个腕尺为人之身高，四腕尺合一步，二十四掌合全身.他在建筑里也用到这些丈量方法，如果你叉开双腿，使身高降低十四分之一，分别举起双臂使中指指尖与头顶齐平，连接伸展的四肢的末端组成一个外接圆，肚脐恰巧在整个圆的中心位置，而两腿当中的空间恰好构成一个等边三角形.而且人在平伸双臂时的宽度等于他的高度.人下跪的时候，他的高度就减少了四分之一等，(24)[意]达芬奇.达芬奇笔记[M].杜莉，译.北京：金城出版社，2011：91.如图43(25)(古罗马)维特鲁威.建筑十书(典藏版)[M].[美]I.D.罗兰，英译，[美]T.N.豪，评注；陈平，中译.北京：北京大学出版社，2019:297..

由上述两端叙述可以知道，维特鲁威实际上给出了人体比例的两个模型，即以肚脐为中心的圆模型和以耻骨为中心的正方形模型.达·芬奇综合并适当调整这两套模型创作了《维特鲁威人》，这超越了维特鲁威，描述了完美的人体比例.《维特鲁威人》中描绘了一个男人在同一位置上的“十字型”和“火字形”的姿态，并同时被分别嵌入到一个矩形和一个圆形中，如图44(26)[意]列奥纳多·达·芬奇. 达·芬奇笔记[M].[美]H·安娜·苏，编.刘勇，译.长沙：湖南科学技术出版社，2015：45..

对于达·芬奇在创作《维特鲁威人》时把人放置在正方形和圆中，有人认为这是达·芬奇对化圆为方的一种尝试(27)Joel Levy. A Curious History of Mathematics: The Big Ideas from Primitive Numbers to Chaos Theory[M]. New York: Metro Books, 2013: 43..

对达·芬奇而言，人类不仅是一个具有无穷无尽的生命力的有机体，也是世界的典范，个人和宇宙的关系正如一面镜子，相互折射，相互映衬，《维特鲁威人》就是达·芬奇对两者关系的完美诠释.

7.2 《马的研究》

马在人类文明发展的进程中扮演了极为重要的角色.在现代文明诞生之前，马是财富的象征，马是身份的象征，马是精神的象征，甚至马是民族和国家文化的象征.自古以来，无论是东方还是西方，马是艺术家们展示自己才华的对象之一.

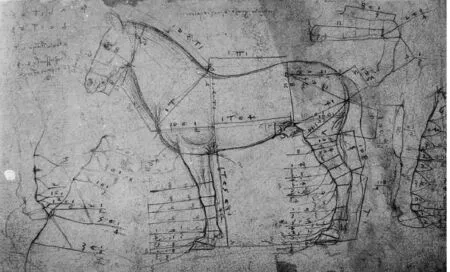
图45 马的身体各部位的数据

既然人体的各组成部分之间存在固定的比例关系，马是否也有类似于人体比例那样的比例关系呢？这是达·芬奇曾经思考的问题.达·芬奇认为：“马的体型是大自然赋予的，他试图从中提取某种‘视觉音乐’.”(28)[英]马丁·肯普.达·芬奇100个里程碑[M].叶芙蓉，译.北京：金盾出版社，2019:60.于是达·芬奇为了掌握马的解剖结构和体型比例，耗费了大量的精力.他以“一匹”和“十六分一匹”为单位详细记录了样本马的测量数据，然后以十六分之一为单位进行分解和二次分解，最后得到了马的体型比例，如图45(29)[英]马丁·肯普.达·芬奇100个里程碑[M].叶芙蓉，译.北京：金盾出版社，2019:61..达·芬奇关于马的艺术作品一般以这种比例为前提而创作的.

8 结语

达·芬奇作为意大利文艺复兴时期的伟人给人类留下了丰富而珍贵的文化遗产，他所做出的贡献达到让人无法想象的地步.他的成长过程、辉煌成就和睿智的思想为人们提供了如无边无际的海洋一般的遐想空间.

首先，科学、艺术、建筑、哲学等所有人类智慧的历史是他的伟大导师.他是欧几里得《几何原本》的研读者；他是毕达哥拉斯、柏拉图和亚里士多德的膜拜者；他是阿基米德力学和军事学的继承者；他是维特鲁威《建筑十书》的超越者；他是绘画为一门科学的提出者；他是解剖学的视觉化展示者；他是人类最高智慧的化身.

其次，达·芬奇是自学成才，不知道什么是系统教育.正因为这样，他的兴趣、所涉猎的领域、工作方式、思维过程等等不受任何所谓“规矩”的束缚.在历史上这样的例子不只达·芬奇一个，还有笛卡儿、爱迪生等等很多.虽然历史是不能假设的，但是我们也不妨假设——如果这些天才们接受了小学、中学和大学的系统而规范的教育，那么情况会如何呢？是不是诸多规范将他们给“规范”死了呢？这是我们每一个教育工作者必须认真思考的问题，从这里也会提出一些教育悖论来.

再次，达·芬奇数学手稿为我们数学教育工作者提供了宝贵的启示，使我们感到今天数学教育过于按部就班，过于教条.从手稿中发现以下几点：1.在小学可以学习三角形的各种形态及其内角和是否等于180°的情形，也可以掌握拓扑学的初步观念；2.在初中可以学习勾股定理的各种表述及由此而引发的曲线形勾股命题、立方体形的勾股命题等等，这对学生的直观想象和猜想能力的培养至关重要；3.数学学习要勤奋，动手动脑，正如欧几里得说的“没有为国王铺设的坦途”那样.达·芬奇的数学学习和研究以及他的数学手稿告诉我们，几何作图能力和直观想象能力的发展是相辅相成的.因此，数学教师要以身作则，引领学生养成动手动脑的习惯和能力，这是数学教学的根本.

最后，让我想起加勒特·汤姆森在《莱布尼茨》序言中的一段引言：“当我评价别人时若出现差错，我宁愿错在宽容他人上.对他人著作的评价也是如此.在著作中，我努力发现的不是应该责怪什么，而是应该赞扬什么，应该从中学到哪些东西.”(30)加勒特·汤姆森.莱布尼茨[M]. 李素霞，杨富斌，译.北京：中华书局，2014:1.达·芬奇虽然是神坛上的天才，但他是一个人.金无足赤，人无完人.达·芬奇的任何一项工作似乎都没有做全，没有完整的系统，而且个别研究中丢三落四或者出现错误.他的手稿是他生前没有来得及整理出版的初稿，因此这些瑕疵的存在是有情可原的，这些绝不会沾污他的伟大，也许会点缀他人生的足迹.

(续完)