数列教学中的数学思想之光

2021-03-24张蜀青

数学通报 2021年2期

张蜀青

(广州市执信中学 510642)

1 引言

等差数列和等比数列是中学数学中最常见的两类数列，不少教师在课堂教学中常常通过一些现实情境、物理常识或者传说引入相关概念．例如在介绍等差数列时，教材通过会场座椅的排列规律引入等差数列的概念，在介绍等比数列时，有些教师通过传说中的国王与数学家(也有说是棋士、年轻人等)以稻谷为赌注下棋的故事引入等比数列．然而，这些情境对于激发学生思考似乎并未产生预期的作用，因为它们并不能反映出等差数列与等比数列深刻的思想内涵．国家课程标准强调数学教学需要密切联系生活，这一理念充分体现在教材中．课程标准也强调数学思想的渗透与学生的数学素养与数学思维能力的提升，这从六大核心素养的提出可见一斑．因此本文通过等比数列求和公式的教学，说明数学课堂中如何在尊重教材的基础上重组内容，充分体现等比数列求和公式的重要性，进而渗透数学思想，为后续的学习做好铺垫．

2 等比数列求和的案例设计

“等比数列的求和公式”一直以来是公开课、说课比赛、教学设计比赛的选材热点．而无论是现实生活还是数学，等比数列都随处可见，例如银行贷款本息的计算便与等比数列有关，物理上原子核的裂变过程也是个等比数列．因此课堂教学中以生活情境为出发点还是以数学情境为出发点并无一定之规，教学过程自然流畅、学生不感到突兀即可．

从纯数学推导过程看，等比数列求和公式并不难，难在如何让学生知其所以然．通常纯数学的表述是这样的：

设an=a1qn-1，n∈N，试求{an}的前n项和Sn．

单纯从传授知识的角度推导求和公式并不难，事实上，记

Sn=a1+a2+…+an，

(1)

在Sn的两边同时乘以公比q得

qSn=a1q+a2q+…+anq

=a2+a3+…+an+1，

(2)

将(1)与(2)两式相减得

(1-q)Sn=a1-an+1.

此处需要讨论q是否为1，如果q≠1则有

学生并不难理解这个推导过程，如果按此方式展开教学，效率还特别高，因而被很多老师采用，还有的老师介绍了多种推导方法，甚至利用因式分解1-qn=(1-q)(1+q+...+qn-1)推导出这个求和公式．然而，这样的教学设计存在几个明显的问题：1.公式的推导和前面的情境是什么关系？假如没有关系，这个问题的情境设置目标是什么？2.为什么会想到乘以q再两式相减？3.过度技巧化的推导方法不仅掩盖了数列求和公式的本质，还可能引发学生的厌学情绪，丧失探究的好奇心．

教育的目的之一是激发学生的学习热情，教会他们用数学家的眼光去观察世界，而不是把数学家思考的结论告诉学生．所以课堂教学不应该仅仅停留在让大多数学生知道怎么做，更重要的是让大家知道为什么这么做，这或许也是课程标准强调教育要结合学生实际生活的原因之一．

而数列教学该从生活情境出发还是数学情境出发？我们在《问题驱动的中学数学课堂教学》[1]中提出了两种方案，一种方案基于生活情境，另一种方案基于数学情境，从教学实践效果的比较看，两者并无本质区别．徐利治先生有一种观点，他认为：“数学教育不妨纯粹一点”(参见[2])．他的意思是，基础教育阶段主要是打基础，学生到了大学可以根据就读的专业再学习如何用数学．虽然不能完全苟同徐先生的观点，但创设情境的确不能为了生活化而生活化．

等比数列在我国古代数学中也不罕见，古人云：“一尺之锤，日取其半，万世不竭”，这段话虽然表达的是极限概念，但一尺长的棍子按上述方法逐段截取后得到的便是一个等比数列．因此，等比数列求和公式的教学也可通过对该问题的改编层层深入地展开．

问题1一尺之锤，日取其半，到第n天一共截取了多少？

日期12…n每天截取的长度1214…12n

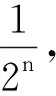
问题2一尺之锤，日取其q(0

分析：每日截取原来的q(0

日期123…n每天截取的长度q(1-q)q(1-q)2q…(1-q)n-1q

则第n天截取之后截取的总长度为

q+(1-q)q+…+(1-q)n-1q，

这个和就具有一般性了，比问题1复杂了许多，但仍然可以采用逆向思维的方法寻求解决的方法．既然是每日截取原来的q(0

日期12…n每天截取后剩余的长度1-q(1-q)2…(1-q)n

由此可得

q+(1-q)q+…+(1-q)n-1q=1-(1-q)n.

显然这个结论适用于任何q(0

如果将1-q换成q，则q也在0与1之间，上式转换成

(3)

有了问题2做基础，就不难拓展到公比q为一般实数的情形了：

问题3(3)式中的q是否对任意正实数都成立？

这里唯一需要启发学生的是，q>1如何转换为0

(4)

及

不难得

而对于q=1，问题是平凡的，学生很容易搞清楚，只需在(4)进行计算时提醒一下分母不能为0．而到问题3还没有把q所有可能的值都考虑到，还需要讨论q<0时的情形.

问题4假如q<0，等式(1)仍然成立吗？

既然学生能懂得当q>1时，取其倒数取而代之，也自然不难明白当q<0时应该用-q取而代之．在此基础之上，回到开始的问题可得一般等比数列{an}的求和公式：

Sn=a1+a2+…+an

至此，一般等比数列的求和公式的推导便大功告成了．

与传统的教学方法相比，上述一系列问题的设计是通过一些学生比较容易理解也方便计算的问题，逐步引导学生发现规律并最终得出求和公式，这里的问题与公式的推导过程是融为一体的，通过特殊的数列帮助学生捕捉到求和公式的信息并逐步得到一般等比数列的求和方法，整个过程一气呵成，形成关于等比数列求和的一个完整认知链，不存在情境与公式推导之间逻辑关系脱节的现象．因此教学过程中情境的创设与问题的解决应该是相呼应的，不能让情境与数学成为没有逻辑关联的两张皮．

3 拓展——现代数学思想之光

基础教育改革进行了很多年，其中一个重要的改革内容是将一部分原来在大学阶段学习的内容“下放”到了中学，让学生初步领略现代数学的魅力，这是必要的，也是国际基础教育改革的趋势．然而，从某种意义上看，数学思想的渗透也许比下放部分数学内容更重要，这种重要性主要体现在两个方面：

(1)思想方法是根本，学习数学知识的最终目的也正是为了掌握数学的思维方法；

(2)通过现代数学思想的渗透，让学生体会现代数学思想的智慧之光，待到他们进入大学，重温这种思想时可以更深刻地理解晦涩的数学内容，从而做到基础教育与大学教育之间的无缝衔接．

等比数列作为一类特殊的数列在数学中的应用是司空见惯的，例如阿基米德为了计算抛物线与直线y=x所围图形的面积，构造了一个特殊的等比数列，成功地计算出了这个图形的面积，这也是积分理论早期的萌芽，教师在讲授定积分理论时完全可以通过阿基米德的算法切入到定积分的定义．等比数列的应用远不止于此，在现代数学中也是经常使用的．例如，著名的康托尔三分集就需要等比数列来计算其测度．康托尔集是现代分形几何中出现的第一个分形集，很多分形集的构造都是基于和康托尔集类似的构造．作为等比数列的拓展，完全可以在课堂上作为一个重要的例子让学生了解这个集合构造的过程．

例1一尺之锤，日取其中段三分之一，第n天取下多少？

这里需要帮助学生搞清楚“日取其中段三分之一”是什么意思，第一日取中段三分之一，留下来两根长度为三分之一的棍子，所以第二日所取是每根棍子中间的三分之一，于是第二日留下了四根棍子，以此类推．这里实际上涉及到了两个等比数列，一是每日留下来的棍子个数，二是每日截下的棍子的长度，如下表：