数学问题解答

(江苏省徐州市第一中学 张培强 221140)

(安徽省旌德中学 赵忠华 242600)

(河南省方城县教研室 邵明宪 473200)

(安徽省南陵县城东实验学校 邹守文 241300)

2021年1月号问题解答

(解答由问题提供人给出)

2581如图1，半径为r、R的⊙B、⊙C外切于点A(R>r)，两圆的一条外公切线与⊙B相切于点D，与⊙C相切于点E，点H1、H2在BC上，且BH1=CH2.过点A作DE的垂线，与过点H1垂直于BC的直线相交于点F1，与过点H2垂直于BC的直线相交于点F2. 求证：

图1

(北京市朝阳区教育研究中心 蒋晓东 100028；北京市朝阳区芳草地国际学校富力分校 郭文征 100121)

证明如图2，连接BD、CE，过点B作BM⊥CE于点M.

图2

因为DE为⊙B、⊙C的切线，D、E为切点，

所以BD⊥DE，CE⊥DE.

所以四边形DBME为矩形.

所以BM∥DE，BD=EM.

所以CM=CE-BD=R-r.

则△F1H1A∽△BMC.

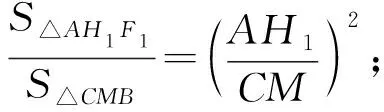
因为BH1=CH2，所以BH2=CH1.

所以BH1+BH2=BH1+CH1=BC.

注意到AH1=BH1-BA，AH2=BH2-BA，

所以AH1+AH2=BH1+BH2-2BA

=BC-2BA=BA+AC-2BA=AC-BA

=R-r. ④

由③和④得

在Rt△BCM中，由勾股定理，得

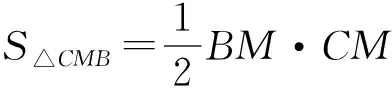
当且仅当点H1、H2重合为BC的中点H时，不等式中的等号成立.

2582设a,b,c,d>0,a+b+c+d=4.求证:

abcd(a2+b2+c2+d2)≤4.

(陕西省咸阳师范学院教育科学学院 安振平 712000)

证明应用调整方法证之.

记f(a,b,c,d)=abcd(a2+b2+c2+d2).

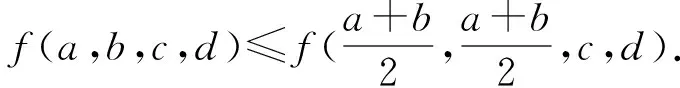
这等价于abcd(a2+b2+c2+d2)

等价于ab(a2+b2)+ab(c2+d2)

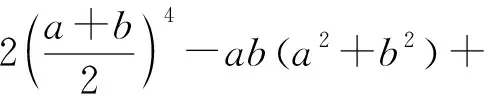
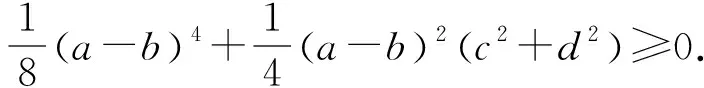
显然成立.

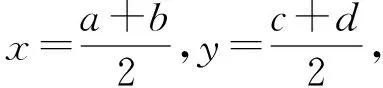
这时，所要证明的不等式等价于

f(x,x,y,y)≤4,也就是 2x2y2(x2+y2)≤4,

注意到xy≤1,所以，只要证明

(2xy)(x2+y2)≤4,

由基本不等式得

综上，知所要证明的不等式成立.

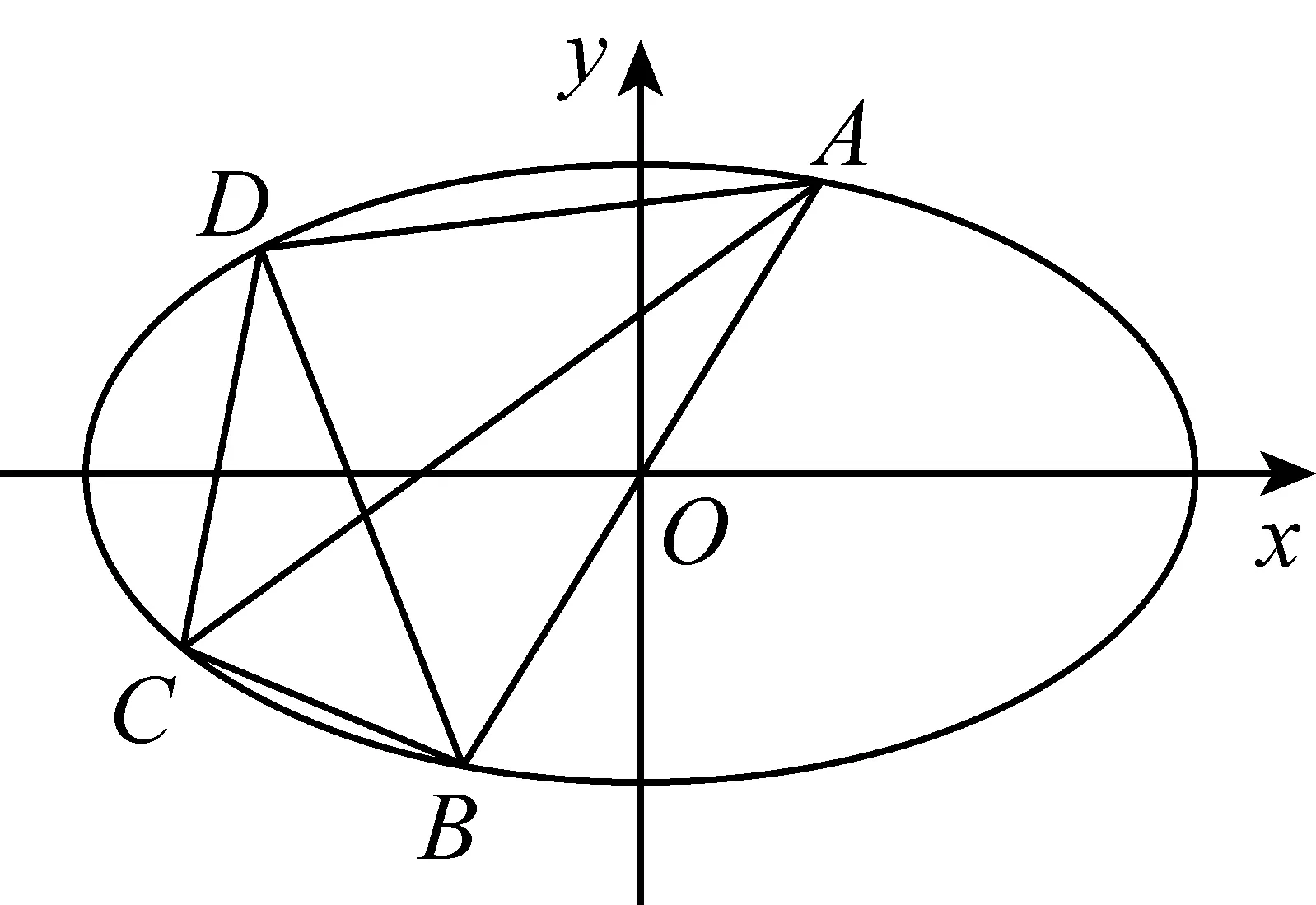
(江苏省徐州市第一中学 张培强 221140)

解设A(acosθ1,bsinθ1)，

B(-acosθ1,-bsinθ1)，

C(acosθ2,bsinθ2)，D(acosθ3,bsinθ3)，

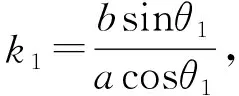
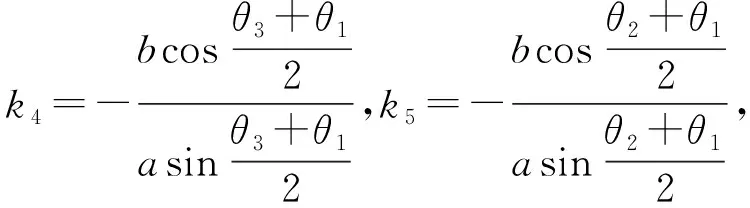
所以

(k1+k3)(k2k4+k2k5)

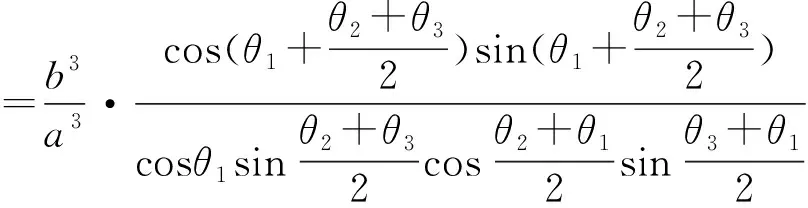
=(k2+k4)(k1k3+k4k6)，得证．

2584在△ABC中，三内角A、B、C所对边长分别为a,b,c，外接圆、内切圆半径和半周长分别为R、r和s.试证：

(浙江湖州市双林中学 李建潮 313012)

证明在△ABC中，由三角形恒等式

有 cosA+cosB+cosC

其次，在(1)式中作三角形代换

有

即

(2)

最后，将三角形恒等式

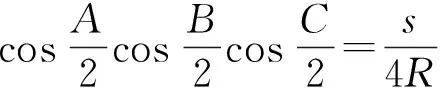
问题得证.

2585如图，点I为△ABC的内心，直线AI,BI,CI分别交线段BC,CA,AB于点D,E,F,记S△BID=S1,S△CID=S2,

(山东省泰安市宁阳第一中学 刘才华 271400)

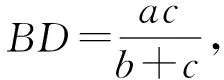
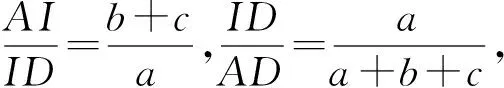
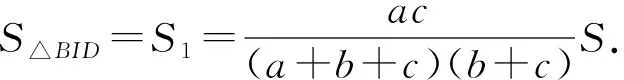
2021年2月号问题

(来稿请注明出处——编者)

2586如图，⊙I是△ABC的内切圆,D,E,F分别是圆与边BC,CA,AB相切的切点，射线DI和EF相交于K.证明：AK平分BC.

(安徽省旌德中学 赵忠华 242600)

2587设a，b，c，d>0，证明：

(河南省方城县教研室 邵明宪 473200)

2588如图，在Rt△ABC中，∠C=90°,BD平分∠ABC,且BD∶AC=2∶3，求证：∠ABC=60°.

(安徽省舒城县杭埠镇中心学校 丁遵标 231323)

2589试证明ex+4x4lnx≥x5+x4.

(安徽省六安第二中学 陶兴红 237005 )

(安徽省南陵县城东实验学校 邹守文 241300)