机器人路径规划算法研究

郑美英，董 航

（辽宁工程职业学院，辽宁 铁岭 112008）

在机器人设计中，路径规划是最基础也是最重要的因素之一，故对其算法研究尤为重要。本文将对传统路径规划算法与智能路径规划算法进行详细研究，并利用MATLAB软件进行算法仿真实验，验证求解路径规划问题的可行性，最后通过对两种算法进行的比较分析，确定最优算法。

一、机器人传统路径规划算法

（一）障碍物分类

机器人设计传统路径规划策略首先需要对环境中的障碍物进行分类，然后再根据障碍物的不同类型设计对应路径规划策略。在具体环境中，障碍物信息由机器人测距传感器实时采集[1]。本文将障碍物信息分为以下四种基本类型（如图1所示）。

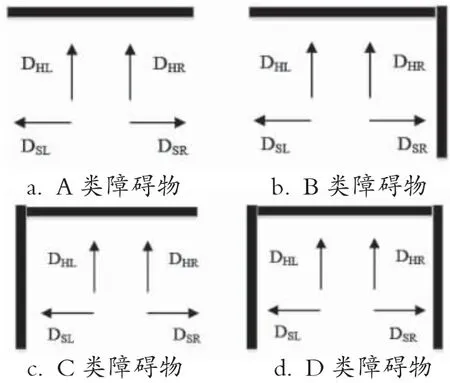
图1 障碍物4种基本类型示意图

图中DSL、DSR、DHL、DHR分别表示机器人车体左侧、车体右侧、车头左侧、车头右侧方向上与障碍物的距离。障碍物四种基本类型说明如下：

A类型：表示在机器人车体的前方有障碍物。

B类型：表示机器人车体的前方与车体右侧有障碍物。

C类型：表示机器人车体的前方与车体左侧有障碍物

D类型：表示机器人的前方、车体左侧、车体右侧都有障碍物。

（二）路径规划策略分析

在具体环境中，障碍物可能有多种类型，但都可概括为上述四种基本类型中的一种或几种类型的不同组合，所以需要分别对这四种基本类型障碍物的路径规划策略进行分析。当机器人四个方向检测不到障碍物时，没有路径规划行为，机器人直行。

在机器人路径规划过程中，为避免机器人与障碍物发生碰撞而损坏机器人，它与障碍物之间必须保持一定距离，即安全距离[2]。安全距离选取过小，机器人在进入路径规划模式前，可能与障碍物发生碰撞，导致路径规划失败；安全距离选取过大会造成机器人提前转向，最终偏离目标点。因此在分析路径规划策略前需要先确定机器人的安全距离[3]。

本研究机器人的转弯方式为两主动轮同时反向旋转带动履带运动从而实现机器人转弯，因此转弯中心即为机器人底盘的几何中心。测得底盘几何中心到履带顶点距离约为200mm，该顶点即为最易先与障碍物发生碰撞的危险点。由于在停车过程中受到惯性的影响，机器人依然会向前运动一段距离，经过多次实验测得此距离约为50mm。为了保险起见，机器人的安全距离选为300mm。

1．A类型障碍物路径规划策略分析

假设满足DHL≤300mm或DHR≤300mm，且DSL≥300mm且DSR≥300mm，就断定机器人此刻处于A类型障碍物环境中。

2．B类型或C类障碍物路径规划策略分析

假设满足DHL≤300mm或DHR≤300mm，且DSL≥300mm且DSR≤300mm，就断定机器人此刻处于B类型障碍物环境中。或者满足DHL≤300mm或DHR≤300mm，且DSL≤300mm且DSR≥300mm，就断定机器人此刻处于C类型障碍物环境中。由于B类型障碍物的路径规划策略与C类型类似，只是障碍物的分布导致机器人转弯方向相反，所以此处以C类型障碍物为例讨论路径规划策略，B类型可以此类推。

3．D类型障碍物路径规划策略分析

假设满足DHL≤300mm或DHR≤300mm，且DSL≤300mm且DSR≤300mm，就断定机器人此刻处于D类型障碍物环境中。

二、基于蚁群算法的机器人路径规划

（一）蚁群算法数学模型

20世纪90年代初，意大利得迪里戈博士团队通过长期对自然界蚂蚁觅食问题的研究提出了一种新型智能算法——蚁群算法（Ant Colony Algorithm，AG）[4]。他们在观察蚁群觅食过程时发现，蚂蚁在搜寻食物时，总是边搜寻边在路径上分泌一种信息素，其它蚂蚁通过识别该信息素来选择距离更短的路径。

（二）蚁群路径规划算法流程

蚁群路径规划算法的运算流程如图2所示。

图2 蚁群路径规划算法流程图

（三）仿真实验与分析

研究蚁群算法α、m、β、ρ、Q、Ncmax等主要参数的最优配置至关重要，但这些参数的配置方法至今未能形成完整的理论体系，所以只能借鉴仿真实验的统计数据[5]。

本文参数设置为α=1、β=15、Q=0.95、m=30、Ncmax=20。设置起点栅格为栅格环境左下角（栅格序号为0），目标点栅格为栅格环境右上角（栅格序号为399）。

图3所示为MATLAB仿真结果，规划出的路径用线条表示。由图可知机器人能寻找到一条从起点出发避开障碍物到达目标点的全局最优路径，同时此路径也为该栅格环境下所能找到的最短路径，路径长度为32.382 m。

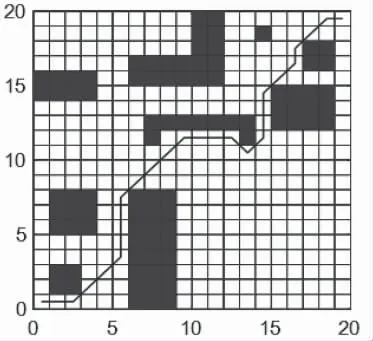
图3 蚁群算法最优路径

图4为蚁群算法收敛结果。由图4可知最短路径长度在迭代7次后收敛于最优路径长度32.382 m，算法运行所消耗的时间为8.515 s。仿真结果验证了蚁群算法解决机器人智能路径规划问题的可行性。

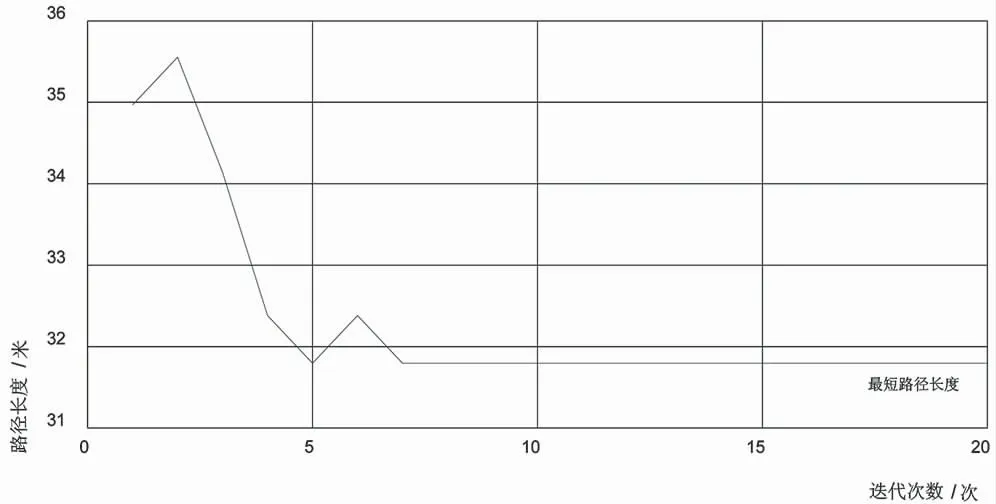
图4 蚁群算法收敛结果

三、基于遗传算法的机器人路径规划

（一）遗传算法数学模型

20世纪70年代初，美国的霍兰博士团队通过长期对达尔文进化论的研究提出了一种新型人工智能算法——遗传算法（Genetic Algorithm，GA）[6]。该算法是模仿自然界物竞天择思想而产生的一种基于遗传理论的算法[7]。目前，在机器人的智能路径规划问题中遗传算法也得到广泛应用。

（二）遗传路径规划算法流程

遗传路径规划算法的运算流程如图5所示。

图5 遗传路径规划算法流程图

（三）仿真实验与分析

与蚁群算法类似，研究遗传算法M、T、Pm、Pc等主要参数的最优配置至关重要，但这些参数的配置方法至今未能形成完整的理论体系，所以只能借鉴仿真实验的统计数据[8]。

在仿真实验前，对种群的各项参数设置如下：种群规模M=60，最大进化代数T=20，交叉概率Pc=0.8，变异概率Pm=0.2。设置起点为栅格环境左下角圆圈处（栅格序号为0），目标点为右上角方格处（栅格序号为399）。

图6所示为MATLAB仿真结果，规划出的路径用线条表示。由图可知机器人能寻找到一条从起点出发避开障碍物到达目标点的全局最优路径，同时此路径也为该栅格环境下所能找到的最短路径，路径长度为30.971 m。

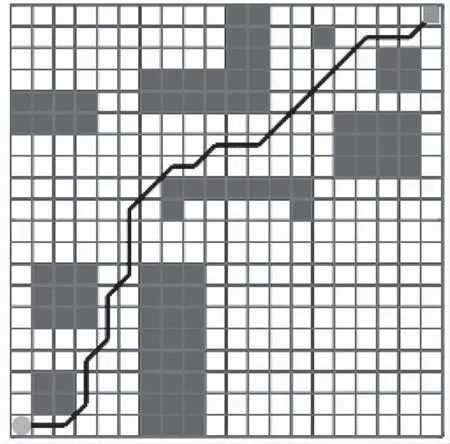
图6 遗传算法最优路径

图7为遗传算法收敛结果，由图可知最短路径长度在迭代10次后收敛于最优路径长度30.971 m，算法运行所消耗的时间为16.402 s。仿真结果验证了遗传算法解决机器人智能路径规划问题的可行性。

图7 遗传算法收敛结果

四、三种算法对比分析

利用智能算法在对机器人进行路径规划时，往往不是毫无要求的，还要附加一些路径距离更短、算法搜索效率更高或算法稳定性更强等限制条件[9]。前面只对蚁群算法与遗传算法进行了MATLAB仿真，验证了蚁群算法与遗传算法求解路径规划问题的可行性。下面将从最短路径长度和最优路径比例两方面对两种智能路径规划算法进行比较分析[10]。为避免一次仿真的偶然性，将这两种算法分别按照之前的设置仿真100次，得到结果如表1所示。

表1 蚁群算法与遗传算法性能比较

由表1可知在最短路径长度方面，遗传算法比蚁群算法所获得的路径更短，说明遗传算法更显智能；在获得最优路径比例方面，遗传算法也远高于蚁群算法说明遗传算法搜索稳定性更好。通过实验比较，遗传算法比蚁群算法具有更智能、更稳定的优点，因此选用遗传算法来解决机器人的路径规划问题。

根据设计要求，机器人应具有路径规划功能，此处可将遗传算法算法应用于解决机器人自主运动过程中的路径规划问题。基于遗传算法的机器人智能路径规划流程如图8所示。

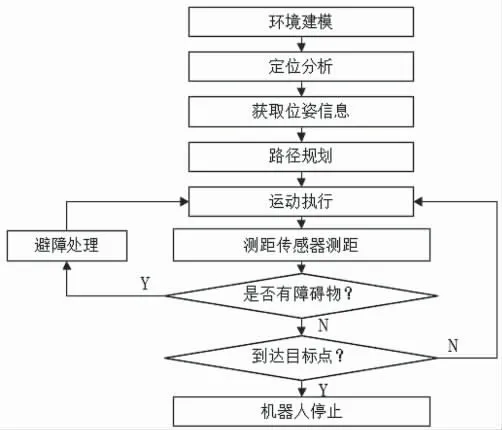
图8 基于遗传算法的机器人智能路径规划流程图

机器人首先向上位机发送定位请求，由定位系统对机器人当前的位置和位姿进行初始标定。在获得机器人位置和位姿信息后，通过获取起始点和目标点及障碍物等信息，调用遗传算法进行全局路径规划，分析规划结果，调用机器人运行程序开始控制机器人行进。若机器人检测到有障碍物，则进入避障处理子程序，最后判断机器人是否已经到达目标点。若是，则本次路径规划任务结束；否则需要重新定位机器人位置信息，再依次进行以上过程，直到到达目标点。

要实现基于遗传算法智能路径规划还需要能获取环境信息的传感器如视觉传感器、激光传感器，由于缺少此类传感器，暂无法获取和处理环境信息。在将来的研究当中将进一步完善机器人环境信息获取和处理能力以实现基于遗传算法的智能路径规划。因此本文最终选择传统路径规划算法来解决机器人自主运动过程中的路径规划问题。

五、结语

本文首先对传统路径规划算法进行了详细介绍，然后对智能路径规划算法研究现状进行了简单介绍，又着重分别对蚁群算法与遗传算法的原理进行了阐述，并叙述了运用这两种算法求解路径规划问题的流程，同时运用MATLAB软件进行了算法仿真实验，验证了蚁群算法与遗传算法求解路径规划问题的可行性。接着从最短路径长度和最优路径比例两个方面对两种算法进行了比较分析。发现遗传算法比蚁群算法具有更智能、更稳定的优点。