输入受限下的四旋翼无人机鲁棒容错控制
2021-03-23刘婷婷宋家友
刘婷婷, 宋家友, 桑 园
(1.郑州西亚斯学院电子信息工程学院,郑州 451150; 2.郑州大学信息工程学院,郑州 450001)
0 引言
多旋翼无人机(UAV)通过控制电机带动螺旋桨旋转,产生升力后可完成多个自由度的飞行运动,进行定高悬停和垂直起降,行动灵活,在军事侦察、航拍、编队表演、勘测等领域发挥着越来越重要的作用,已成为研究的热点[1-3]。由于多旋翼UAV在飞行过程中不断抖动,容易出现机械和电气故障,严重时还会造成UAV坠毁,所以对飞行控制系统的依赖性极高[4]。另外,多旋翼UAV的旋翼能提供的升力有限,在设计容错控制律时,需要充分考虑输入受限的影响[5-7]。
近些年,对多旋翼UAV容错控制的研究已经取得了一定成果。文献[8]针对四旋翼UAV轨迹跟踪的容错控制问题,提出了一种基于鲁棒控制和干扰观测器的容错控制方法,能够准确估计外界干扰和执行器加性故障,实现了UAV的容错控制,并通过仿真验证了方法的有效性。四旋翼UAV在执行高负荷和长航时任务时,旋翼的疲劳断裂容易导致UAV失控甚至坠毁。文献[9]针对悬停状态下四旋翼UAV的执行机构故障,提出了一种基于插值增益调度PID的主动容错控制方法,通过多模型故障诊断算法准确估计了执行器故障,并根据估计结果,动态切换控制律,实现了UAV的容错控制,但设计过程较为复杂;文献[10]提出了一种基于积分滑模控制的四旋翼UAV主动容错控制方法,通过构造观测器对执行机构故障进行实时观测,并设计了积分滑模控制律,通过对UAV的位置和姿态控制回路进行补偿,具有较强的容错能力。
在输入受限的情况下,本文充分考虑了执行器故障和外界干扰对四旋翼UAV的影响,提出了一种鲁棒容错控制方法,针对UAV的位置故障模型和姿态故障模型,分别设计鲁棒容错控制律,并通过模糊系统逼近未知项,实现了包容执行器故障和外界干扰的四旋翼UAV全状态鲁棒容错控制。
1 建立四旋翼UAV故障模型
四旋翼UAV是螺旋桨呈十字交叉布局的小型飞行器,体积小巧、结构紧凑,结构图如图1所示。

图1 四旋翼UAV结构图
图1中,旋翼1和旋翼3顺时针转动,旋翼2和旋翼4逆时针转动,工作时产生向上的升力[11-13]。由于UAV的4个旋翼的转速是有极限值的,并且容易发生失效故障,则4个旋翼在UAV位置环和姿态环所产生的气动力和气动力矩同样存在受限和失效两种情况。
接下来,分别对旋翼执行器受限及失效故障下的四旋翼UAV位置模型和姿态模型进行描述。
1.1 四旋翼UAV位置模型
综合考虑外部干扰、执行器受限以及执行器失效故障的影响,四旋翼UAV位置模型[14-15]可描述为
(1)
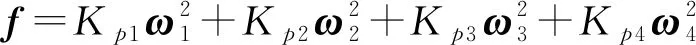
本文采用双曲正切函数来逼近受限函数,可以表示为
(2)
逼近误差为
Δ(f)=sat(f)-h(f)。
(3)
利用拉格朗日中值定理,将式(1)四旋翼UAV位置模型化简为
(4)

(5)
(6)

1.2 四旋翼UAV姿态模型
综合考虑外部干扰、执行器受限以及执行器失效故障的影响,四旋翼UAV姿态模型[16-17]可描述为
(7)
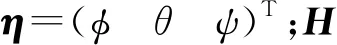
(8)
式中:l为旋翼轴心到UAV重心的距离;CD为UAV的反扭矩系数。
四旋翼UAV的位置故障模型和姿态故障模型建成后,就可以进行容错控制律的设计。
2 鲁棒容错控制律设计
针对外界干扰、执行器受限以及执行器故障情况下的四旋翼UAV位置模型和姿态模型,本文设计了自适应容错控制律,在设计过程中,将位置模型分为位置回路和速度回路逐步进行分析,并将姿态模型分为姿态角回路和角速度回路逐步分析,利用模糊系统[18-19]对未知项进行估计,从而实现对四旋翼UAV的鲁棒容错控制。鲁棒容错控制系统结构如图2所示。

图2 鲁棒容错控制系统
2.1 位置环鲁棒容错控制律设计
针对提出的四旋翼UAV的位置故障模型,设计了鲁棒容错控制律。
2.1.1 位置回路
(9)
对式(9)求导可得
(10)
设计虚拟控制指令vd为
(11)
式中,k1>0,是正定矩阵。为避免“微分爆炸”,将vd通过滑模滤波器
(12)
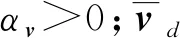
(13)
对式(13)求导可得
(14)

2.1.2 速度回路
令v的跟踪误差为
(15)
对式(15)求导可得
(16)
(17)
式中:Wv是参数向量;ξv是基函数向量;εv是误差。选取滑模面为
(18)
式中,a>0,是正定矩阵。对式(18)求导,并将式(16)、式(17)代入可得
(19)
设计四旋翼UAV位置环的鲁棒容错控制律为
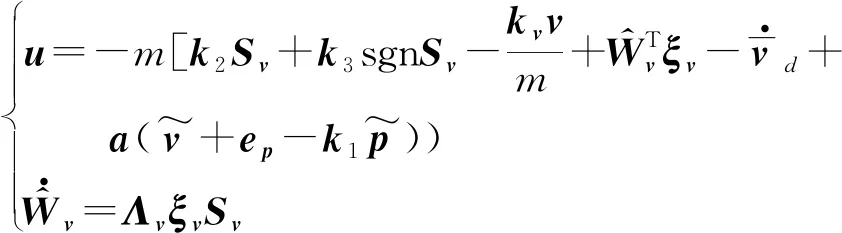
(20)
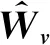
2.1.3 稳定性证明
证明过程如下。考虑如下Lyapunov函数
(21)

(22)
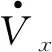
由控制指令u的表达式解算得到UAV的俯仰角指令θd和滚转角指令φd的表达式为
(23)
(24)
式中,ψd为人为输入的UAV偏航角指令。
2.2 姿态环容错控制律设计
针对提出的四旋翼UAV的姿态故障模型,设计了鲁棒容错控制律。
2.2.1 姿态角回路
(25)
对式(25)求导可得
(26)
设计虚拟控制指令Ωd为
(27)
式中,kη为正定矩阵。将Ωd通过滑模滤波器进行滤波后,输出到角速度回路中,即
(28)
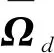
(29)
对式(29)求导可得
(30)

2.2.2 角速度回路
令角速度跟踪误差为
(31)
对式(31)求导可得
(32)
利用模糊系统对未知项Δ进行逼近,则
(33)
式中:Wη表示最优参数向量;ξη表示模糊基函数向量;εη表示误差。
选取滑模面为
(34)
式中,aη为正定矩阵。对式(34)求导,并将式(32)、式(33)代入可得
(35)
设计四旋翼UAV姿态环的鲁棒容错控制律
(36)
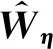
2.2.3 稳定性证明
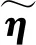
证明过程如下。考虑如下Lyapunov函数
(37)
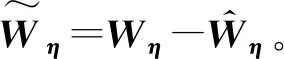
(38)
由于四旋翼UAV在实际飞行中,各参数都是有界的,因此可以得到下列不等式
(39)


(40)
式中:I3为单位阵。
(41)
3 仿真验证与对比分析
为了验证本文提出的鲁棒容错控制律在四旋翼UAV中的控制效果,在Matlab环境中进行了仿真验证。四旋翼UAV参数如表1所示。
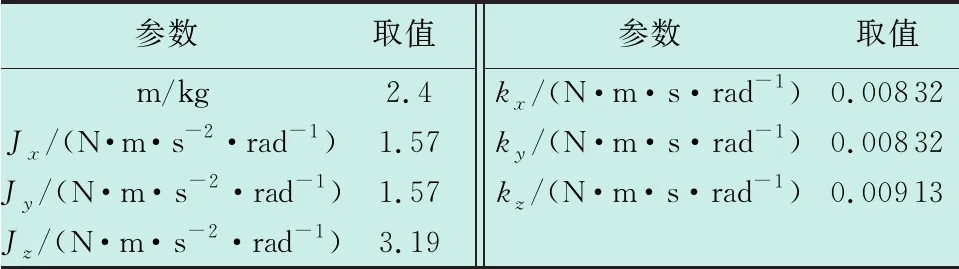
表1 四旋翼UAV参数
设定仿真时间为30 s,四旋翼UAV的位置指令(xdydzd)T=(20sin 0.8t30sint25sin 1.2t)T,偏航角指令ψd=6sin 1.6t,外界干扰dη=(dx,dy,dz)T=(0.2sint0.2sin 0.5t0.3sin 2t)T。故障设置:当t=10 s时,四旋翼UAV位置环发生执行器故障,故障因子sx=sy=sz=0.65;当t=20 s时,四旋翼UAV姿态环发生执行器故障,故障因数E=diag(0.7,0.6,0.65);输入限制为f∈[0,50],单位N,Γf i∈[-3,3],i=p1,q,r,单位N·m。经过调试,选取鲁棒容错控制律的参数如表2所示。

表2 鲁棒容错控制律参数
为了验证本文方法具有更好的鲁棒性和容错性,分别采用控制律式(20)、式(23)、式(24)、式(26)与文献[10]中设计的积分滑模容错控制律进行对比仿真,得到的结果见图3~图8,分别为位置(x,y,z)、滚转角φ、俯仰角θ和偏航角ψ的仿真曲线。误差分别为ex=x-xd,ey=y-yd,ez=z-zd,eφ=φ-φd,eθ=θ-θd,eψ=ψ-ψd。
从仿真结果可看出:执行器故障未发生时,本文所设计的鲁棒容错控制律能够在输入受限的情况下,克服外界干扰的影响,精确跟踪指令信号;而文献[10]所设计的控制律会在指令附近小幅振荡,说明本文控制律在输入受限下,对外界干扰具有较强的鲁棒性。另外,当t=10 s和t=20 s,四旋翼UAV执行器发生不同程度的故障时,在本文所设计的鲁棒容错控制律的作用下,仿真曲线在轻微振荡后,能够快速准确跟踪指令信号;而在文献[10]所设计控制律的作用下,仿真曲线的振荡幅度和频率都比较大。这也进一步说明了本文所设计的鲁棒容错控制律在输入受限情况下,对执行器故障具有较好的容错性。

图3 x仿真曲线

图4 y仿真曲线
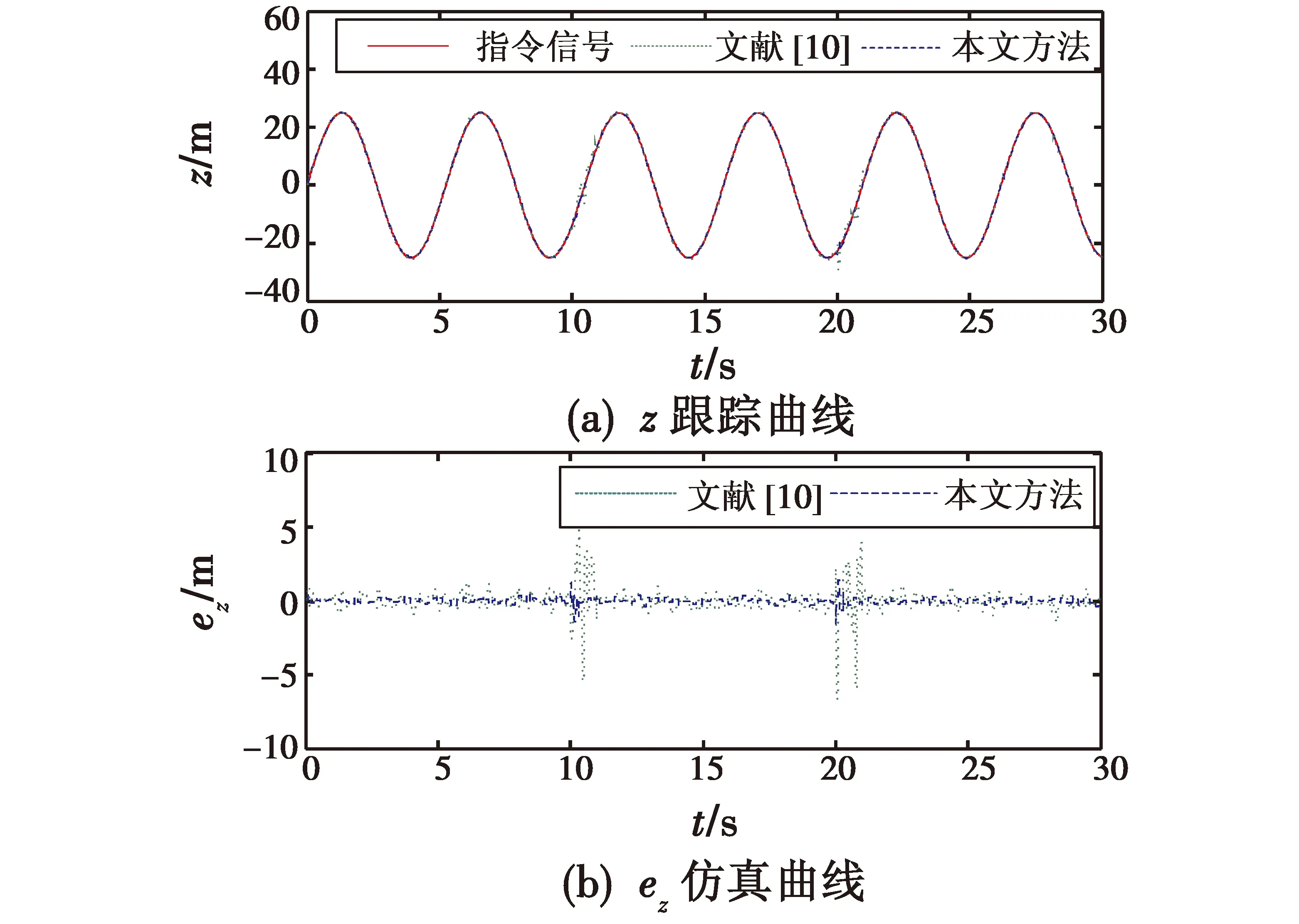
图5 z仿真曲线

图6 滚转角仿真曲线

图7 俯仰角仿真曲线

图8 偏航角仿真曲线
另外,得到的合力f以及力矩Γf仿真曲线分别如图9和图10所示。
从图9和图10可以看出,本文所设计的鲁棒容错控制律能够在实现包容执行器故障以及外界干扰的四旋翼UAV鲁棒容错控制的前提下,确保合力f和力矩Γf在规定的输入限制区间内。
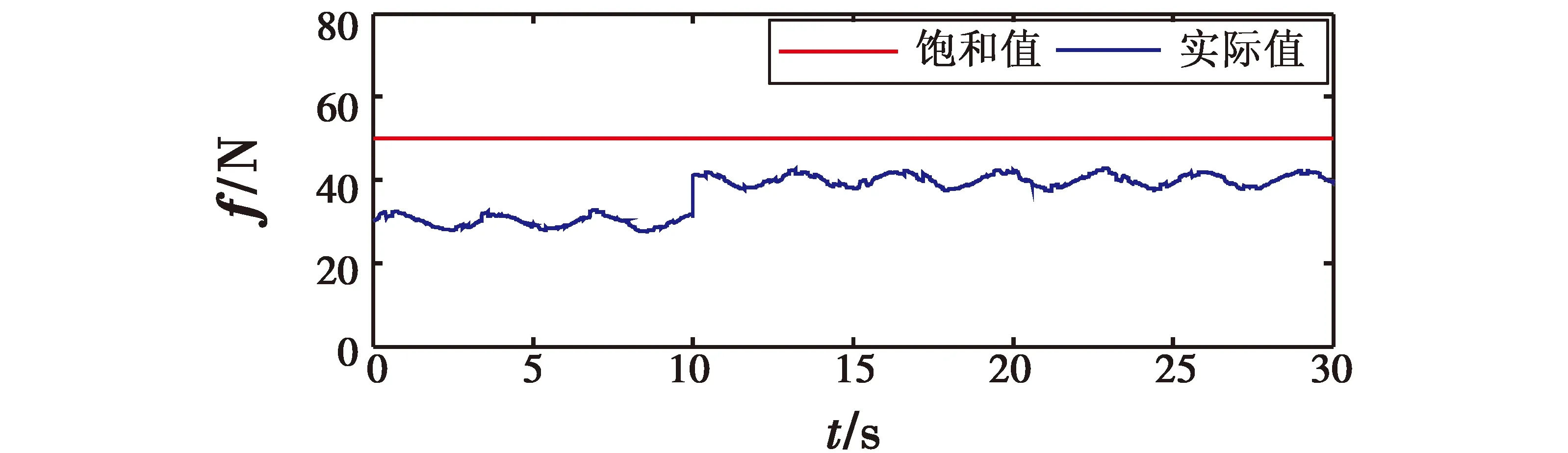
图9 合力f仿真曲线

图10 力矩Γf仿真曲线
为了验证模糊系统能够精确估计UAV位置模型和姿态模型中的未知项,得到未知项估计结果如图11所示。
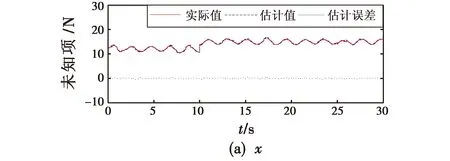
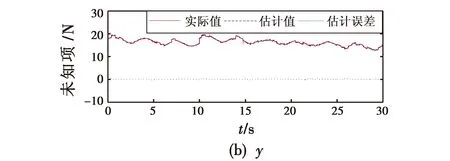

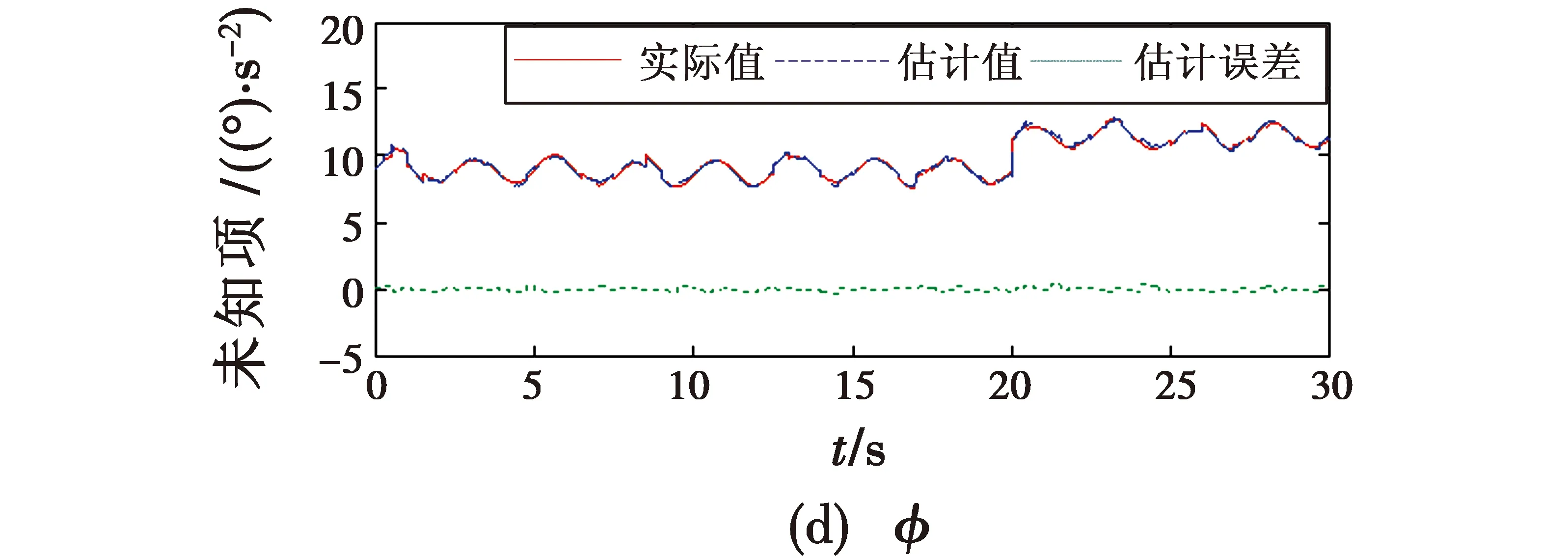


图11 未知项估计结果
从图11可以看出,本文所设计的模糊系统能够准确估计UAV位置模型和姿态模型中的未知项,从估计误差可以明显看出,对未知项的估计效果非常好。
综上所述,本文设计的鲁棒容错控制律能够在输入受限情况下,通过模糊系统准确估计未知项,实现包容外界干扰和执行器故障的UAV鲁棒容错控制,并且控制性能较好。
4 结束语
针对四旋翼UAV在输入受限下的执行器故障,提出了一种鲁棒容错控制方法,经过Matlab仿真验证,可以得到以下结论:
1) 设计的鲁棒容错控制律对外界干扰具有较好的鲁棒性,能够快速、准确跟踪指令信号;
2) 设计的鲁棒容错控制律对执行器故障具有较好的容错性,与积分滑模容错控制律相比具有更好的控制效果;
3) 设计的鲁棒容错控制律能够实现包容执行器故障以及外界干扰的鲁棒容错控制,并且能够确保升力以及力矩满足四旋翼UAV的输入限制。
