基于深度卷积自编码器的短距慢动目标检测

扶 明， 郑 霖， 杨 超， 黄凤青， 邓小芳， 刘争红

(1.桂林电子科技大学广西无线宽带通信与信号处理重点实验室，广西 桂林 541004；2.通信网信息传输与分发技术重点实验室，石家庄 050081)

0 引言

慢速运动目标的有效检测是短距雷达的重要目标之一，实际检测环境中，目标雷达截面积(Radar Cross Section，RCS)小，回波能量微弱，同时接收到的回波信号中包含大量的背景噪声和杂波，其能量往往大于目标信号的能量，导致待检测目标被淹没在这些噪声和杂波中[1]，这些因素都使得短距雷达的慢速目标检测变得困难。传统方法中有基于运动目标指示(Moving Target Indication，MTI)和相参积累，以及子空间投影等目标检测方法被应用于雷达系统。MTI是依据杂波与目标回波多普勒的差异来滤除零频附近的杂波，保留远离零频的运动目标[2-3]。但对慢动目标来说，当运动目标靠近零频时，MTI滤波器对其多普勒成分有极大衰减，使得检测性能并不理想[4]。基于子空间投影的目标检测方法主要是对回波信号特征分解，依据特征值谱的性质分离杂波特征分量并突显目标信号。然而，子空间方法一般要假定杂波子空间的维数[5]以及目标信号子空间与杂波子空间的独立性[3,6]，但在实际情况中杂波子空间具有多维度特性，并且特征空间会出现交叠，导致目标检测性能下降。另外，基于时频分析的目标检测方法，存在时频聚集程度低等缺点[7]，当运动目标的多普勒频移与杂波接近时，这些方法不能有效地检测出目标[8]。

近年来，随着深度学习的迅猛发展，其在雷达信号处理领域也被广泛应用[9-12]。文献[10]中采用超宽带雷达得到不同物体的雷达回波信号，并生成距离—多普勒(Range-Doppler，R-D) 谱图，然后将其送入3种卷积神经网络中对不同目标分类识别以控制机器人的行为；文献[11]则研究一维雷达信号的特性，采用卷积神经网络用于汽车雷达的杂波和噪声分类，以期望实现复杂检测场景的准确分类；文献[12]基于快速的区域卷积神经网络(Faster R-CNN)对R-D谱中的目标特征和杂波特征自动提取，可以避免复杂的手工设计特征，最后完成了对R-D谱中杂波的高精度分类和识别。现有多数利用神经网络的方法大都是如上述实现对被检测目标的分类与识别，抑或基于神经网络学习杂波特征然后对杂波分类。而对于本文场景来说，需要从杂波和噪声干扰严重的复杂背景中检测出目标，并进一步处理获取目标的运动信息，因此，本文期望利用神经网络理论对回波信号的R-D谱中的杂波和目标信号进行特征学习以实现杂波的端到端抑制，最终完成慢动目标的检测。

本文考虑到传统目标检测方法对慢动目标检测存在局限性，依据上述思路，设计了一种深度卷积自编码器网络的目标检测方法。首先，卷积层对R-D谱进行编码以学习相关的杂波信号特性，提取运动目标信号隐含特征，然后反卷积层解码以重构目标信号，最后实现端对端的杂波抑制，并在输出层恢复出相对纯净的运动目标。其中，通过在网络中引入双通道的结构，以同时提取到回波信号的幅度信息与相位信息，以及设计了一种跳跃连接的结构，在减轻梯度消散问题的同时，能有效地提取R-D谱中的目标特征，提高目标检测性能，并能使网络训练更加高效。实验证明了该方法的有效性。

1 回波信号模型

考虑一个单基地脉冲多普勒雷达，设其发射信号为

(1)

式中：uh(t)为第h个发射脉冲的复包络；fc为载波频率；Tr为脉冲重复周期；Tc为Chirp信号扫频时长。则运动目标的回波模型为

x(t,h)=αuh(t-τ(t))exp(j2πfc(t-τ(t)))+c(t)+n(t)

(2)

式中：α为回波信号的衰减系数；τ(t)为目标回波相对于发射信号的延时；c(t)为杂波；n(t)为高斯白噪声。将回波信号x(t)重排成快慢时间维回波矩阵，对快时间维进行脉冲压缩，对慢时间维进行傅里叶变换，可以得到回波信号的R-D谱，通过对R-D谱中的目标进行检测，从中可以提取到目标的距离信息和径向速度信息。

2 基于深度卷积自编码器的目标检测方法

2.1 卷积自编码器

卷积神经网络[13](Convolutional Neural Network,CNN)与其他网络相比，有局部连接与权值共享两个不同之处。局部连接即每个神经元只与上一层网络的一小块区域的部分神经元相连，减少了很多参数且考虑到了像素之间的位置信息；而权值共享使得神经元不再是每个连接都有对应不同的权重，而是一组连接可共享同一权重，减少需要训练的权值个数，降低网络的计算复杂度。

自动编码器(Auto-Encoder，AE)是一种旨在将输入复制到输出的神经网络。AE通过编码器(Encoder)可以学习到输入数据的隐含特征，然后解码器(Decoder)用新学习到的特征重构出原始输入数据，常用于对数据的降维或去噪。而卷积自编码器(Convolutional Auto-Encoder，CAE)主要是利用卷积神经网络中的卷积层与池化层代替AE中的全连接层。

2.2 具有跳跃连接结构的双通道卷积自编码器网络

本文设计了一种如图1所示的双通道卷积自编码器模型，就其中一条通道来说，该模型主要由3层卷积层(Convolution Layer,Conv)、6个残差块，以及3层反卷积层[14](Deconvolution Layer，deConv)组成，其中，3层卷积层为编码器网络，3层反卷积层为解码器网络。

图1 基于跳跃连接的双通道卷积自编码器网络模型

编码器网络中，为了减少计算量，卷积核大小都设置为“3×3”。同时，为了压缩特征图尺寸，卷积核滑动步长依次为1,2,2，卷积核个数依次设置为256,128,64。解码器网络为了恢复被压缩的特征图尺寸，保持输出尺寸与输入相同，其超参数设置与解码器网络正好相反。

深度网络训练时模型参数的不断改变，会造成内部协变量偏移(Internal Covariate Shift)现象，导致网络训练速度慢且效率低下[15]。因此在每一个卷积层和反卷积层后都接一个批标准化(Batch Normalization，BN)层，对网络每一中间层的输入做标准化处理。网络神经元激活函数使用带泄露的修正线性单元 (Leaky Rectified Linear Unit, Leaky ReLU)函数，并设置系数a为0.2，主要是为了防止训练时出现“Dead Neuron”，即ReLU激活函数在输入为负数时输出为零，如

f(x)=max(ax,x)。

(3)

为了更深层地提取回波数据的特征，本文模型增加了卷积层的层数，考虑到这样会带来梯度消散问题，甚至网络的性能退化[16]，因此本文模型使用了一种残差结构块(ResBlock)，如图2所示。残差块的卷积层卷积核大小为[3,3]，滑动步长为1，卷积核的数量为64。

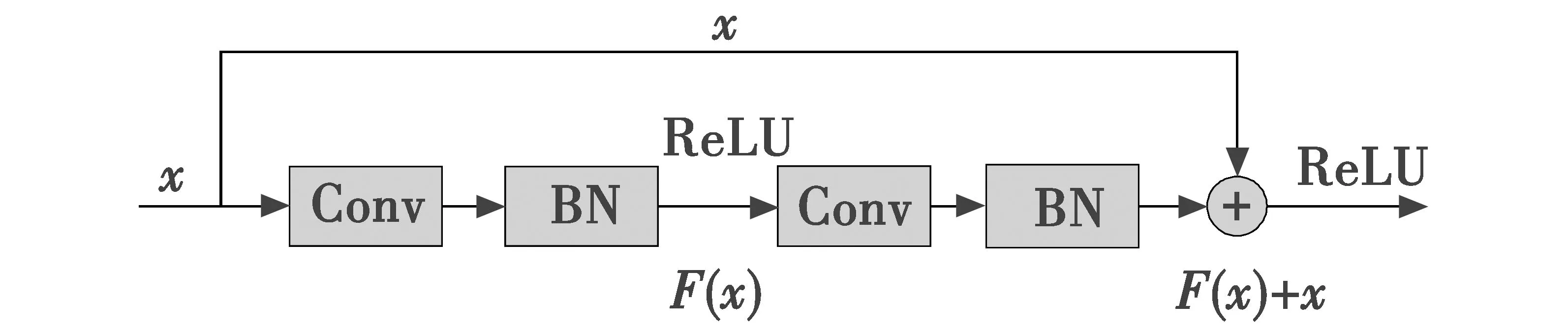
图2 残差块结构

本文检测场景中因探测目标本身的RCS较小，回波能量微弱，并且目标在时频谱上尺度较小，本文网络模型删除了可能降低特征图分辨率的池化层，使用了全卷积网络模型。考虑在低分辨率雷达中，目标在时频谱上成像为点目标，其尺度较小，且解码器网络中的反卷积层可能无法从抽象的特征中很好地恢复目标细节，因此设计了一种跳跃连接结构，即将编码器中的3个卷积层，跳过中间的各层，与解码器中相应的3个反卷积层直接连接，如图1所示，其中连接时将卷积操作后的特征图以特征通道进行串接。当网络很深时，运动目标隐含特征细节尽管会丢失，但是跳跃连接传递的特征包含了很多原始输入的细节，有助于反卷积更好地恢复目标信号特征。而且跳跃连接还有另一个好处是在反向传播时可以将梯度从底层传递到顶层，缓解了整个网络训练时的梯度消散问题。

另外，当雷达接收端接收IQ两路信号时，如果只考虑其中之一，难免会丢失回波信号的部分信息，因此，将回波数据R-D谱的实部矩阵与虚部矩阵分别送入本模型中两个子编码器进行特征学习，以提取到回波信号的幅度与相位特征，然后经过3个残差块以继续进行深层特征的提取，最后将提取的特征进行融合，这样保证了回波信号在输入时的信息完整度，神经网络可以提取到更多特征，有助于后续的目标检测。

3 实验结果与分析

3.1 仿真实验及分析

为验证算法的有效性，本文进行了相应的实验。如式(1)所示回波模型，非平稳回波数据由目标回波、瑞利杂波以及高斯白噪声组成，系统参数如表1所示。

表1 雷达系统参数

实验在Matlab R2016b平台上进行仿真分析，在表1所示系统参数的条件下产生回波信号的R-D谱以及相应纯净目标回波的R-D谱，以构建样本数据集。其中在回波中预先设置运动目标，考虑为近距离慢速目标，从速度取值范围为-3.4～3.5 m/s、距离取值范围为20～50 m随机选取其速度值与距离值，速度的正负值表示运动的方向。

仿真产生回波样本数据共100 000个，并基于TensorFlow框架，搭建出如图1所示的神经网络结构，随后将样本数据送入网络中训练学习。

为检验算法的有效性，设置了相应的对比实验，实验中，采用同样方式生成雷达回波数据，并在其中注入一个距离为40 m、步行速度为2 m/s的运动目标，以检验本文方法，并与传统的杂波抑制目标检测算法进行对比。图3分别为传统目标检测算法与本文方法的检测结果比较。

图3 传统目标检测算法与本文CAE方法检测结果比较

由图3可得，MTI方法与子空间方法虽然抑制掉了部分杂波或干扰，但并不能很好地检测出目标。这是因为MTI的本质是在零多普勒附近产生凹陷来抑制杂波的，所以会同样抑制处于零多普勒频率附近慢动目标的部分能量，特别当杂波能量比较大时，经MTI处理过后的残余杂波仍然会淹没掉目标；而子空间方法一般采用最大的一个或几个特征值对应的特征向量来构建杂波子空间，这样会使杂波成分出现较大残余，并且杂波子空间常常呈现多维度及交织特性，也无法有效地分离出杂波基；本文CAE网络模型检测结果则表现比较好，相对前两者来说杂波抑制得比较干净，能很清晰地分辨出目标在R-D谱上的位置。

模拟多目标检测场景时，雷达回波中预先设置两个运动目标，其中一个距离为40 m，步行速度为2 m/s，另一个距离为30 m，步行速度为-1 m/s。图4为本文基于CAE的检测方法与传统检测方法的检测结果对比。可以看出，本文CAE方法在多目标检测场景中相对于传统方法也有较好的检测效果。

图4 多目标检测场景中传统目标检测算法与本文CAE方法检测结果比较

另外，本文还与基于深度学习的方法进行了对比，主要考虑：基于本文的CAE网络基本结构，其去掉跳跃连接且仅为单通道，并将其命名为CAE-1；以及基于本节的CAE网络基本结构，其具有跳跃连接但仅为单通道，将其命名为CAE-2；与这两者进行对比，对最后的检测结果与网络损失函数的Loss值曲线进行了分析。其中，3种网络模型中除了上述说明的不同，基本的网络超参数，例如卷积核尺寸、滑动步长，网络层数等均为相同的设置。

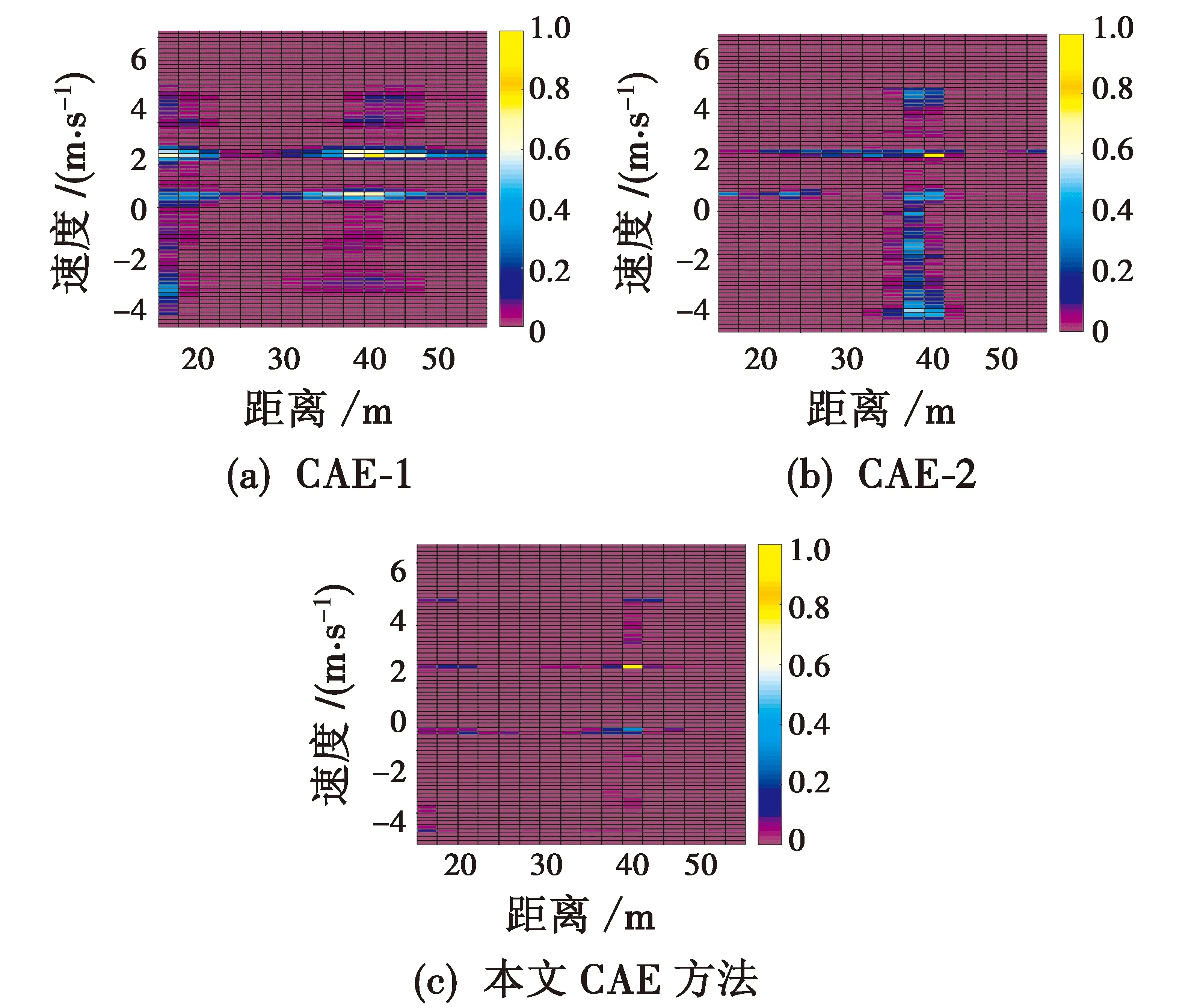
图5 CAE及改进算法的检测性能比较

图5为3种基于神经网络的检测结果。图5(a)中，单通道的CAE网络检测结果显示目标周围有较强的干扰，使得检测效果不佳；图5(b)中单通道CAE网络中加入了跳跃连接结构后，检测效果明显得到了改善，这是因为跳跃连接结构减少了神经网络在训练过程中的信息损失，有利于目标的检测；图5(c)中双通道结构更完整地利用了回波信号的信息，而跳跃连接结构使目标信号在解码器中被更完好地重构，因此与前两种方法相比，该方法能很清晰地检测出目标。分别将图5(a)与图5(b)相对比、图5(b)与图5(c)相对比，验证了网络中跳跃连接结构与双通道结构对于提高目标检测性能的有效性。

图6为3种网络结构中每个Batch在训练时的Loss函数值随训练次数增加的曲线图，表示了神经网络的收敛趋势。由图6中可以看出，具有跳跃结构的CAE网络(红色曲线与蓝色曲线)收敛趋势相差不大，但相比无跳跃连接结构的CAE网络(绿色曲线)，其收敛得更快，且网络收敛曲线趋于平稳时Loss函数的值更小，证明了具有跳跃结构的网络在训练时相比于无跳跃结构的网络更具有高效性。

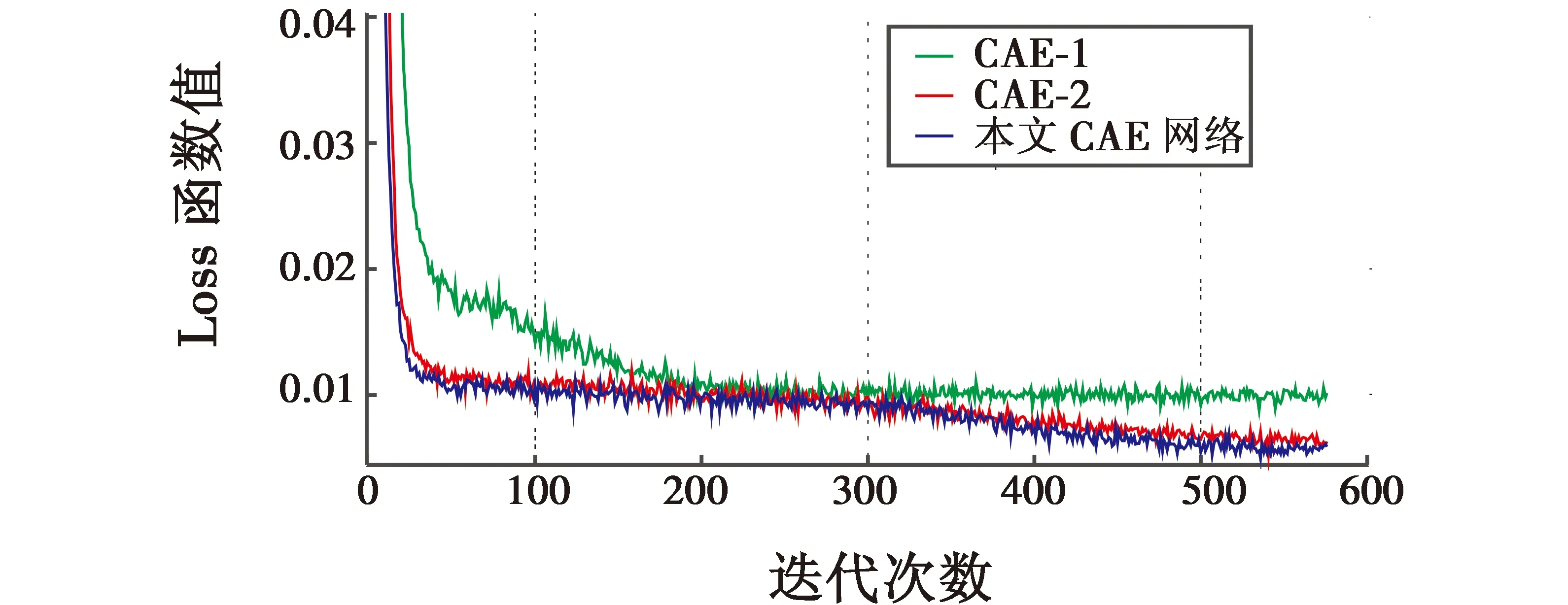
图6 Loss Batch曲线图

3.2 实测数据处理

为了进一步验证本文方法的有效性,采集了实际场景数据进行测试。实验中利用了LabVIEW软件结合通用软件无线电外设(Universal Software Radio Peripheral, USRP)硬件搭建NI USRP-2974数据采集平台。如图7所示，数据采集装置由USRP上位机、USRP、板状天线(RX，TX)等构成，通过上位机编程结合硬件实现雷达波形数据发送与接收，其中，编程中采用的波形参数及硬件射频参数配置与仿真相同, USRP发射功率设为2 dBm。

图7 实测场景

图8所示分别为2阶MTI算法、子空间法以及本文CAE网络对实际场景数据的处理结果。图8(a)所用的传统MTI滤波器，在抑制了杂波成分的同时，也抑制了慢速运动目标的多普勒成分；图8(b)采用子空间方法，在R-D谱中仍有残余部分杂波和噪声；图8(c)为本文方法，从中可以看到目标能被较清晰地检测到，其中，运动人体目标距离大概为35 m，速度为0.6 m/s左右。

图8 实测数据处理时，传统目标检测算法与本文CAE方法检测结果比较

4 结束语

本文针对在低RCS、杂波或干扰严重环境下的短距离慢速目标检测问题，设计了一种具有跳跃连接的双通道卷积自编码器的目标检测算法。利用CAE中编码器对距离-多普勒图中的目标信号成分和杂波成分进行特征学习，并提取运动目标信号隐含特征，然后反卷积层解码以重构目标信号，最后实现端对端的杂波抑制。另外，网络采用了双通道的结构以更完整地提取目标回波特征，并且考虑到网络模型较深，设计了跳跃连接的结构，减少了梯度消散问题，增强了信息在网络中的流动，使网络训练时更高效。实验验证了该算法的有效性及较传统方法有更好的性能表现。