移动空间光通信中光斑中心检测算法分析

沈天浩， 田开坤， 梁赫西， 代永红， 艾 勇

(1.湖北师范大学，湖北 黄石 435002； 2.武汉大学电子信息学院，武汉 430072)

0 引言

高速粗跟踪系统是移动空间光通信系统的核心组成部分，其关键技术在于快速检测光斑中心位置[1-2]。目前，常用的光斑中心检测算法有Hough变换算法、圆拟合算法以及灰度重心算法。在Hough变换算法中，需要逐点投票、记录，其时间复杂度较高,计算所需时间较长[3]；圆拟合算法虽然运算精度高，但其抗干扰能力差，容易受到随机噪声的影响[4]；基于灰度重心算法的结构简单明了，可应用于光斑光强比较均匀的条件下，但在实际测量中，其时间算法复杂度比较大，容易受到光斑形状和背景的限制。

本文在传统灰度重心算法的基础上加以改进，在计算光斑中心前对光斑进行中值滤波和自适应二值化处理，可有效提高系统抗干扰能力，其后粗识别光斑中心位置，最后经过选框重心计算获取光斑精确位置。

1 基于灰度重心的激光光斑检测算法

灰度重心算法是利用灰度为权值的加权型算法[5]。在大小为M·N的灰度图像中，设光斑的灰度权值为S(i,j)，则灰度重心法计算的光斑(x0,y0)为

(1)

该方法受背景灰度值和目标灰度值的影响较大，若目标灰度值较大、背景灰度值较小，使用灰度重心法可以计算得到较为精确的光斑中心坐标。但实际环境中，大部分目标灰度值与背景灰度值相差较小，用灰度值作为权值的计算方法作用有限[6]。

在移动空间光通信中，发射端发射激光受到大气湍流效应的影响容易出现较大散射和干扰[7]，CCD相机接收的光斑形状大小不同，对准确识别光斑中心造成较大困难。传统灰度重心算法要求光斑形状对称性好、时间复杂度高且抗干扰能力差，因此在移动空间光通信系统中不适用。

2 改进重心算法

本文在传统灰度重心算法的基础上加以改进，结合中值滤波和自适应阈值二值化的原理，在计算光斑重心之前将图像进行预处理。改进的灰度重心算法的框图如图1所示。

图1 改进重心算法框图

CCD相机采集光斑图像，中值滤波消除激光光斑的噪声点；图像进行二值化处理分离背景与光斑；然后利用粗识别算法对光斑中心位置进行粗定位，为了提高计算光斑中心位置精度，对可选取光斑的范围进行重心计算，获取精确的光斑中心。

2.1 滤波去噪

激光在自由空间中传输一段距离后会受到尘埃、颗粒等影响，在形成光斑的同时会随机产生一些耀斑和暗斑，这些斑点容易影响识别的精度，可采用一些滤波的方法减少斑点导致的误差。

常用的滤波方法有均值滤波、高斯滤波、中值滤波等[8]。均值滤波利用图像中任意一个像素点是其周围A·B个像素值的均值，主要用于滤除椒盐噪声。高斯滤波主要是对图像进行加权平均处理，每个像素值都由其本身和周围A·B个像素值经过加权平均后计算得到，主要用于滤除高斯噪声。中值滤波是比较A·B区域的像素值大小，将取出的中值作为该区域的中心点像素值，适用于滤除椒盐噪声，同时也能保留图像的细节。本文采用中值滤波的方法滤除光斑中的椒盐噪声。

2.2 自适应二值化处理

图像二值化是将灰度图像中的像素值设置为0或1,一般0代表黑色，1代表白色。图像二值化能够凸显图像中目标的轮廓，使图像变得更加简单，数据量更小。图像二值化常用的有全局二值化、局部二值化和自适应二值化[9]。全局二值化通过设置一个固定的阈值T，将图像分为两个部分，大于T的像素点为1(或者0)，小于T的像素点为0(或者1)，但全局二值化非常容易破坏图像的细节。局部二值化是利用一定规则将图像分为N个区域，在每个区域设置一个阈值T，将该区域内的图像分为两个部分，但该方法阈值T没有经过计算，仍然会出现一些图像细节被破坏。局部自适应二值化可以一定的方法计算出局部的二值化适当阈值，减少对图像细节的破坏。

本文利用自适应二值化法对光斑进行二值化处理分离光斑与背景。局部自适应法主要是对每个像素确定一个以自身为中心的领域窗口，取该领域内像素的最大值和最小值,然后求平均值作为阈值[10]。

2.3 粗识别光斑中心算法

图像在经过滤波处理和二值化后，利用如下算法可计算得到粗识别光斑算法。

1) 将原始图像转化为灰度图像，再利用自适应二值化将图像数字化处理，最后转换为一个二维数组，其中二维数组的元素对应灰度图像的像素值。其转换见图2。

图2 图像数字化处理图

2) 二维数组进行压缩行处理，将二维数组的每一列相加得到一维数组LR。二维数组的每一行相加得到一维数组LC。以图2为例，其一维数组LR和LC分别为LR=(0,0,…,4,5,…,42,56,…,56,42,…,13,8,5,0,…,0,0)，LC=(0,0,…,11,21,…,44,47,…,47,44,…,20,13,11,0,…,0,0)。

3) 取一维数组LR最大值的索引，该索引为光斑中心横坐标x0；取一维数组LC最大值的索引，该索引为光斑中心纵坐标y0。根据上述算法可计算出光斑中心位置为(105.0,95.0)(单位，像素)，时间代价为0.000 62 s。如图3所示。

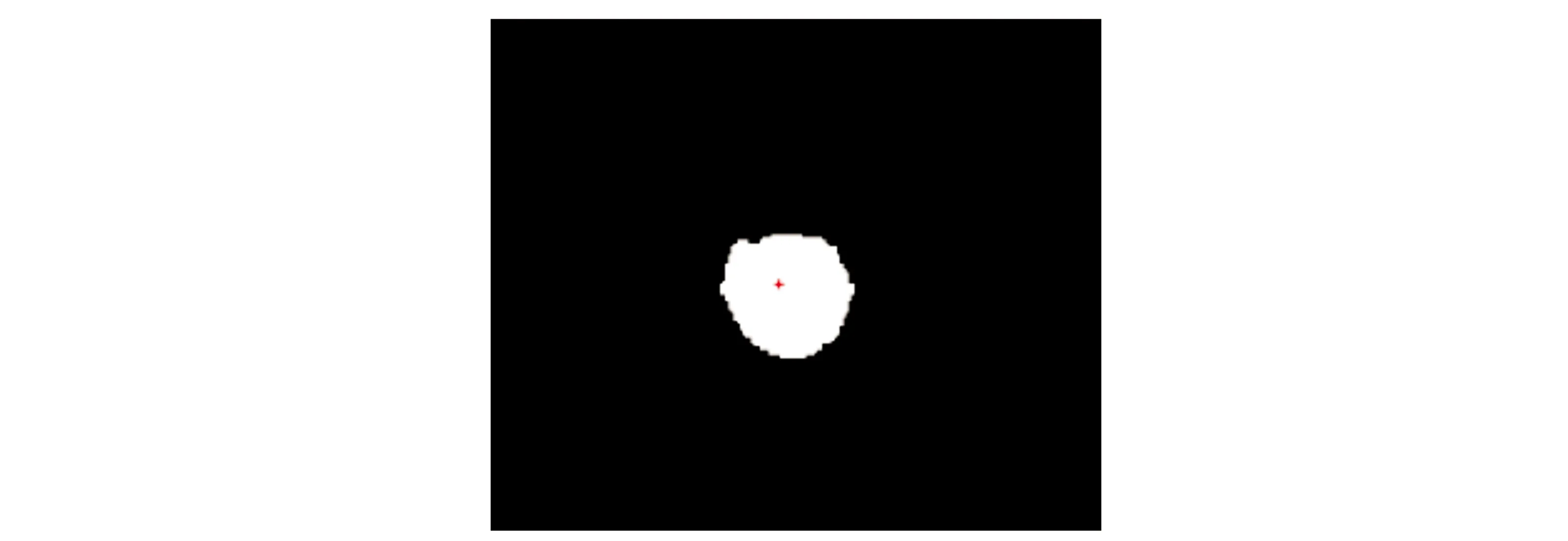
图3 粗识别算法计算的光斑中心

2.4 选框计算

由于粗识别光斑算法中易出现多个最大值，使得光斑识别误差比较大，为了提高光斑中心识别的精度，可根据粗识别的光斑中心位置为中心点，利用边缘检测算法选取光斑的大小[11]，其选框的原则是在确保运算速度的前提下，提高运算精度。最后通过式(1)计算光斑中心位置。

3 实验及结果

激光在空间传输过程中会受到大气湍流和空气中一些微粒的影响，能量分布不均匀，形成形状不规则的光斑，使得不同位置光斑的形状和光斑的亮度有较大区别[12]。将激光器放置在转台上并发射650 nm激光，通过平行光管输出平行激光，在距离激光器10 m处利用CMOS图像传感器接收激光，并利用上述算法计算光斑中心位置。在实验中主要选取3个不同位置的光斑，从时间代价和运算精度两方面与灰度重心算法进行对比,实验如图4～图6所示，实验数据利用Python语言编写程序完成实验分析。

实验利用感光芯片OV5647采集光斑数据，其靶面大小为8.5 mm×8.5 mm,设置CCD相机图像开窗大小为320×240，默认光斑最亮点为光斑中心，对光斑实际测量并估算出光斑中心点坐标。实验选取3个移动光斑的位置，分别得到图4中光斑位于中心右侧,原始光斑最强点估算为(132.983，73.962)(单位，像素)，图5中光斑位于中心上侧,原始光斑最强点估算为(107.489，54.992)(单位，像素)，图6中光斑位于中心,原始光斑最强点估算为(106.996，97.980)(单位，像素)。综合上述实验可对灰度重心算法与改进的重心算法进行对比分析，如表1所示。

图4 光斑位于中心的右侧

图5 光斑位于中心的上侧

图6 光斑位于中心

表1 灰度重心算法与改进的重心算法对比

通过表1可知，灰度重心算法和改进重心算法在光斑中心识别精度相差不大，但在时间代价上改进重心算法更小，提高约一个数量级。

图3的实验数据是利用粗识别算法计算可得光斑中心坐标为(105.0,95.0)(单位，像素),在粗识别光斑算法基础上加入选框计算后，构成改进重心算法,计算其光斑中心坐标为 (107.158,97.857)(单位，像素)，与估算光斑中心坐标(106.996，97.980)(单位，像素)进行对比，改进重心算法在计算精度方面比粗识别算法更高。二者时间代价对比，粗识别算法计算图3的时间代价为0.000 62 s，改进重心算法时间代价为0.004 86 s。粗识别算法计算光斑速度快、精度低。加入选框计算方法后构成改进重心算法可以提高光斑中心计算精度，但时间代价增大。综合对比传统灰度重心算法、粗识别算法和改进重心算法这3种算法，改进重心算法更适用于移动空间光通信领域的光斑中心识别的精度和速度的要求，应用于移动空间光通信领域。

4 结束语

本文提出了一种改进灰度重心算法，在检测光斑中心前加入中值滤波，自适应二值化阈值处理，经过粗识别光斑中心位置后选框计算获取光斑精确位置。实验表明，传统灰度重心算法检测光斑中心的时间代价约为0.024 s，本文提出的改进算法时间代价提高了约一个数量级。改进重心算法计算光斑中心的精度高、速度快，可应用于移动空间光通信系统、激光定位、光斑识别等领域，该算法也可提高光斑识别系统的抗干扰性能。