分数阶Sprott-F不确定混沌系统的适应滑模同步

王东晓,雷腾飞,毛北行

(1. 郑州航空工业管理学院 数学学院,郑州 450015；2. 齐鲁理工学院 机电工程学院,济南 250200)

目前,混沌同步已引起人们广泛关注[1-2],随着分数阶微分建模方法的发展及滑模方法的引入,分数阶混沌系统的滑模控制研究已取得了较多成果[3-4],其中不确定项和外部扰动在实际系统中大量存在,如文献[5-6]分别用自适应滑模和终端滑模方法研究了不确定分数阶Victor-Carmen混沌系统及Duffling混沌系统的同步问题；文献[7]研究了分数阶不确定混沌系统的异结构同步问题；文献[8]研究了不确定分数阶Genesio-Tesi系统的适应转移滑模同步问题；文献[9]用两种方法研究了不确定Newton-Leipnik分数阶系统滑模同步；文献[10]基于滑模控制研究了分数阶不确定超混沌金融系统的同步；文献[11]研究了Bao超混沌分数阶系统的比例积分滑模同步. 由于Sprott混沌系统代表一大类非线性混沌系统,且应用广泛,因此已引起人们广泛关注. 如文献[12]研究了Sprott-Ⅰ混沌系统的动力学解析问题; 文献[13-14]研究了二维Sprott系统的分析、控制和同步问题; 文献[15]研究了Sprott-O含参系统的延迟反馈同步; 文献[16]研究了Sprott-D系统的H∞同步; 文献[17]研究了分数阶Sprott-C系统的适应滑模同步；文献[18]研究了Sprott-F系统的混沌反控制. 但关于不确定分数阶Sprott-F混沌系统滑模同步的研究目前文献报道较少,基于此,本文研究分数阶具有不确定项和外部扰动Sprott-F混沌系统适应滑模同步,通过构造合适的分数阶滑模面和控制律及适应规则,得到不确定分数阶Sprott-F混沌系统取得自适应滑模同步的两个充分条件.

1 主要结果

定义1[19]Caputo分数阶导数定义为

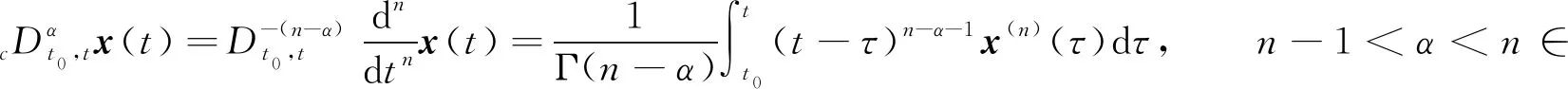
分数阶Sprott-F混沌系统为

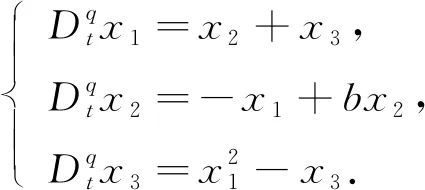
(1)

当b=0.5,q=0.95时,系统(1)的吸引子如图1所示.

以系统(1)为主系统,设计从系统为

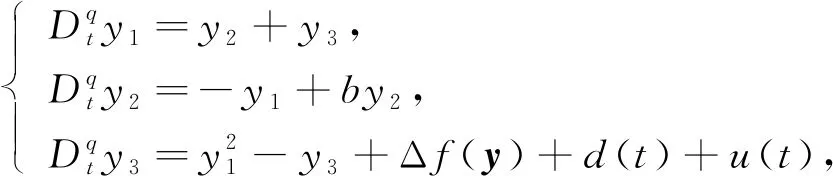
(2)

其中Δf(y)为系统的不确定项,y=(y1,y2,y3),d(t)为有界的外部扰动,u(t)为控制器. 由于系统存在不确定项和外部扰动项,因此系统不是混沌态. 定义ei=yi-xi,可得

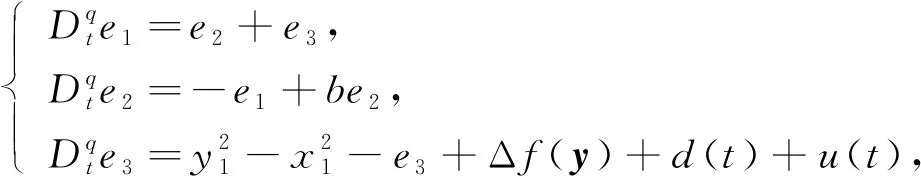
(3)

加上不确定项和扰动后,系统阶数变化下的动力学行为如图2所示.

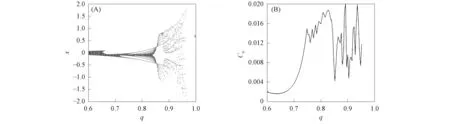
图2 阶数变化下的动力学行为Fig.2 Dynamic behavior under change of order

假设1|Δf(y)|≤m,|d(t)|≤n,其中未知参数m,n>0.

引理1[19]若x(t)为连续可微函数,则对∀t≥t0,有

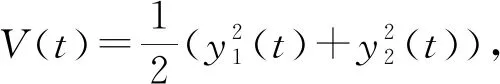
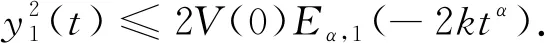
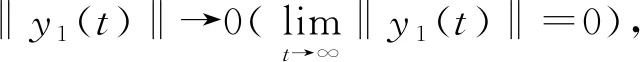
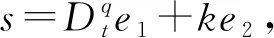
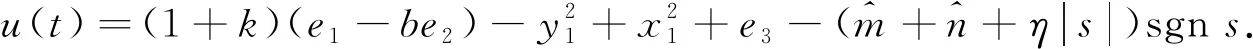
(4)

适应规则为

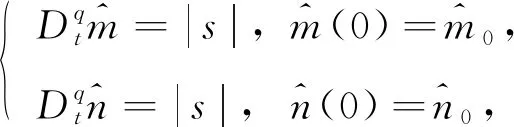
(5)

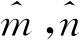
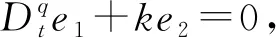
从而得到分数阶微分方程

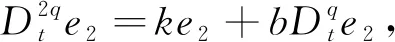
(6)

对式(6)利用Laplace变换,并记E2(s)=L(e2(t)),可得

利用Laplace终值定理得

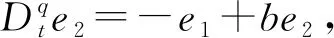
不在滑模面上时,构造函数

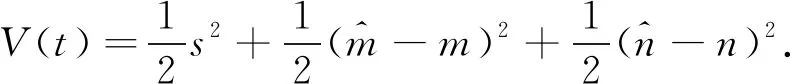
(7)

由引理1,求分数阶导数得

考虑整数阶Sprott-F混沌系统

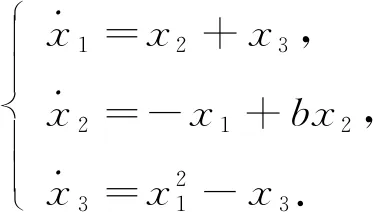
(8)

以系统(8)为主系统,设计从系统为

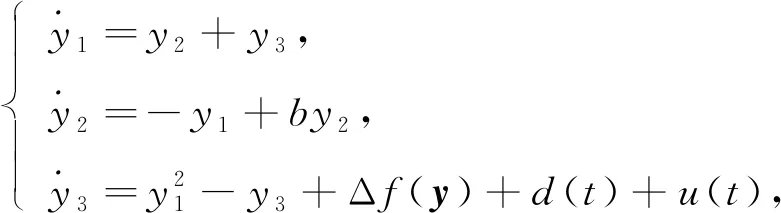
(9)

其中Δf(y)为系统的不确定项,y=(y1,y2,y3),d(t)为有界的外部扰动,u(t)为控制器,定义ei=yi-xi,可得

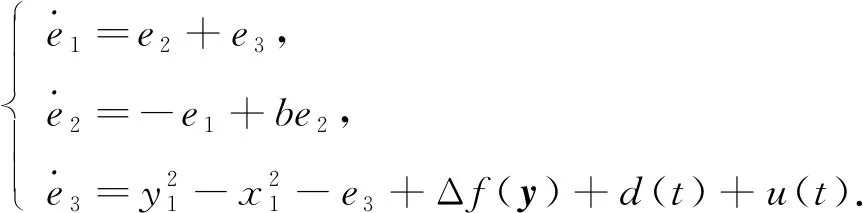
(10)

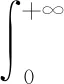
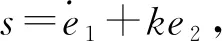
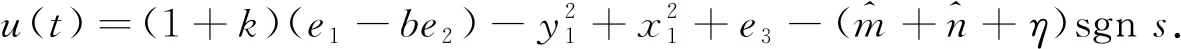
(11)

适应规则为

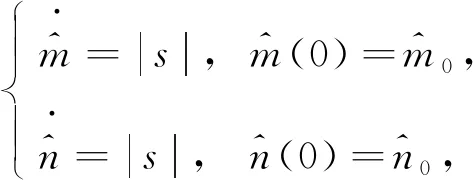
(12)

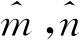
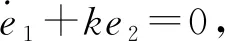
不在滑模面上时,构造函数(7)，由引理1,求分数阶导数得

2 数值仿真

用MATLAB进行数值仿真. 参数分别为

b=0.5,q=0.95, Δf(y)=0.5cos(2πy3),d(t)=0.6sin(t),

初始值设为

(x1(0),x2(0),x3(0))=(0.1,0.2,0.1),η=1,k=3.

加上不确定项和扰动后,系统阶数变化下的动力学行为如图2所示. 由图2可见,加入控制器后,一段时间后系统呈分岔特性,当q>0.95时,定理1和定理2的系统误差曲线分别如图3和图4所示.

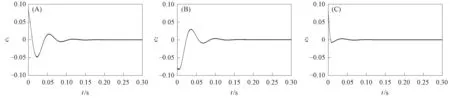
图3 定理1中的系统误差曲线Fig.3 Systematic error curves in theorem 1

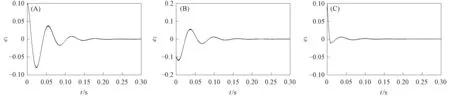
图4 定理2中的系统误差曲线Fig.4 Systematic error curves in theorem 2

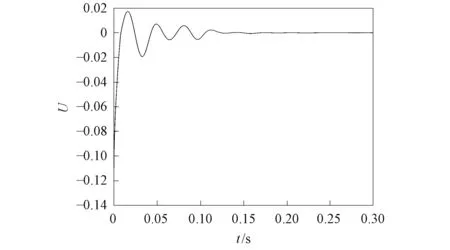
图5 定理1中加入控制器后的变化曲线Fig.5 Change curve after adding controllers in theorem 1

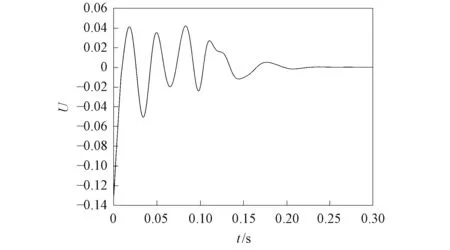
图6 定理2中加入控制器后的变化曲线Fig.6 Change curve after adding controllers in theorem 2

由图3和图4可见,误差动态系统在初始时相差较大,且距原点较远,一段时间后逐渐趋近于坐标原点,表明分数阶Sprott混沌系统的主从系统取得了滑模同步. 在定理1和定理2中加入控制器后的变化曲线分别如图5和图6所示. 由图5和图6可见,当初始时刻未加入控制器时,控制输入量为零,加入控制器后,控制量随时间的增加而发生变化,当系统取得滑模同步时,系统的控制量稳定为常数值. 定理1和定理2的滑模函数变化曲线分别如图7和图8所示. 由图7和图8可见,一段时间后滑模面趋近于坐标原点,系统状态可被驱动到原点并沿滑模面移动到坐标原点,从而达到滑模动态控制的理想效果. 定理1选取分数阶滑模面,定理2选取整数阶滑模面,定理2是定理1的特例. 该研究结果表明,定理1的结论可推广到整数阶系统,因此对定理2也适用. 与用全息的动态误差函数作为滑模面相比,本文用半截误差函数作为滑模面,因而滑模面的形式更简单,用控制输入的方式较易将误差动态系统驱动到滑模面,在滑模趋近阶段可沿滑模面快速趋近于坐标原点,从而达到对分数阶Sprott混沌系统进行同步控制的目的.

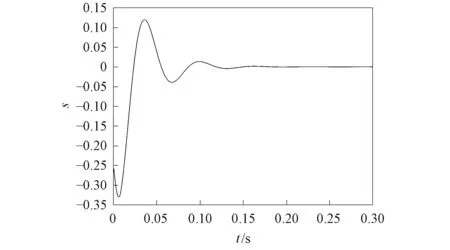
图7 定理1中滑模函数的变化曲线Fig.7 Change curve of sliding mode function in theorem 1

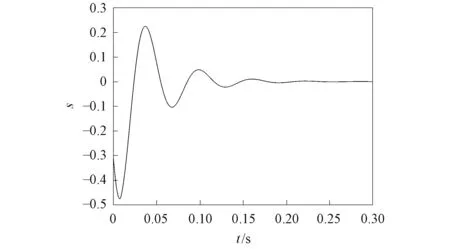
图8 定理2中滑模函数的变化曲线Fig.8 Change curve of sliding mode function in theorem 2

综上,本文研究了具有不确定项和外部扰动分数阶Sprott-F混沌系统的适应滑模同步,通过构造合适的滑模面,得到不确定分数阶Sprott-F混沌系统取得适应滑模同步的两个充分条件. 研究表明,不确定Sprott-F混沌系统在一定假设下是适应滑模同步的,并将分数阶的研究结论推广到整数阶.