基于随机森林优化的自组织神经网络算法

李永丽,王 浩,金喜子

(1. 东北师范大学 信息科学与技术学院,长春 130117；2. 吉林大学 计算机科学与技术学院,长春 130012)

在数据分析处理过程中,数据的影响因素数目和维度会影响后期数据预测与分析的准确性,它们之间存在正相关关系,因此在数据处理过程中应尽可能多地考虑存在的影响因素. 但数据维度和影响因素的增加会导致数据处理过程复杂,提高时间和空间的复杂度,为保证数据的可处理性及可使用性,需在数据挖掘中降低问题的复杂度,因此可引入特征降维的分析方法(如主成分分析(PCA)方法). 在深度学习的数据处理过程中,也需进行数据降维处理,以达到减少运算量和数据降噪的目的. 神经网络的训练集一般具有多组特征,将这些特征作为输入并进行趋势预测前,通常用降维特征向量算法. 如文献[1]提出了一种主成分分析-多层感知器(PCA-MLP)模型；文献[2]将多层感知器(MLP)等多种算法用于高速公路车流量预测；文献[3]提出了一种基于行为的信用卡诈骗预测模型. 虽然去除特征量中的冗余和干扰数据并对数据进行降维处理,在某些应用场景中能显著提高预测准确率[4],但当数据集的多组特征与结果都具有较强的相关性时,降维处理可能会导致预测准确性降低. 针对该问题,本文提出一种基于随机森林算法优化的MLP回归预测模型,该模型在数据预处理后将数据集按数据属性进行划分,并在全连接神经网络的中间层与输出层回归分类器之间,使用随机森林算法对MLP回归模型的隐藏状态进行纠正,该过程主要纠正在降维时被忽略的部分要素.

1 预备知识

1.1 特征降维算法

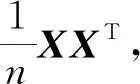
1.2 随机森林算法

随机森林算法是利用多个树型数据结构,对样本进行训练并预测的一种算法,它既可以应用在分类问题中,也可以用于数据的回归分析. 随机森林与传统决策树算法不同,其具有不剪枝也能避免数据过拟合的特点,同时具有较快的训练速度,且参数调整简单,在默认参数下即具有较好的回归预测效果[6-7]. 图1为随机森林模型. 其利用bootstrap方法从原始训练集中随机抽取n个样本(有放回),并构建n个决策树(图1显示了两棵决策树)；在这些样本中选择最好的特征(图1中Feature(f))进行分裂,直至该节点的所有训练样例都属于同一类,然后使每棵决策树在不做任何修剪的前提下最大限度生长,最后将生成的多棵分类树组成随机森林,并用其进行分类和回归. 随机森林算法最终结果由多个分类器投票或取均值确定,即计算每棵树条件概率Pn(c|f)的平均值[8].

1.3 MLP回归模型

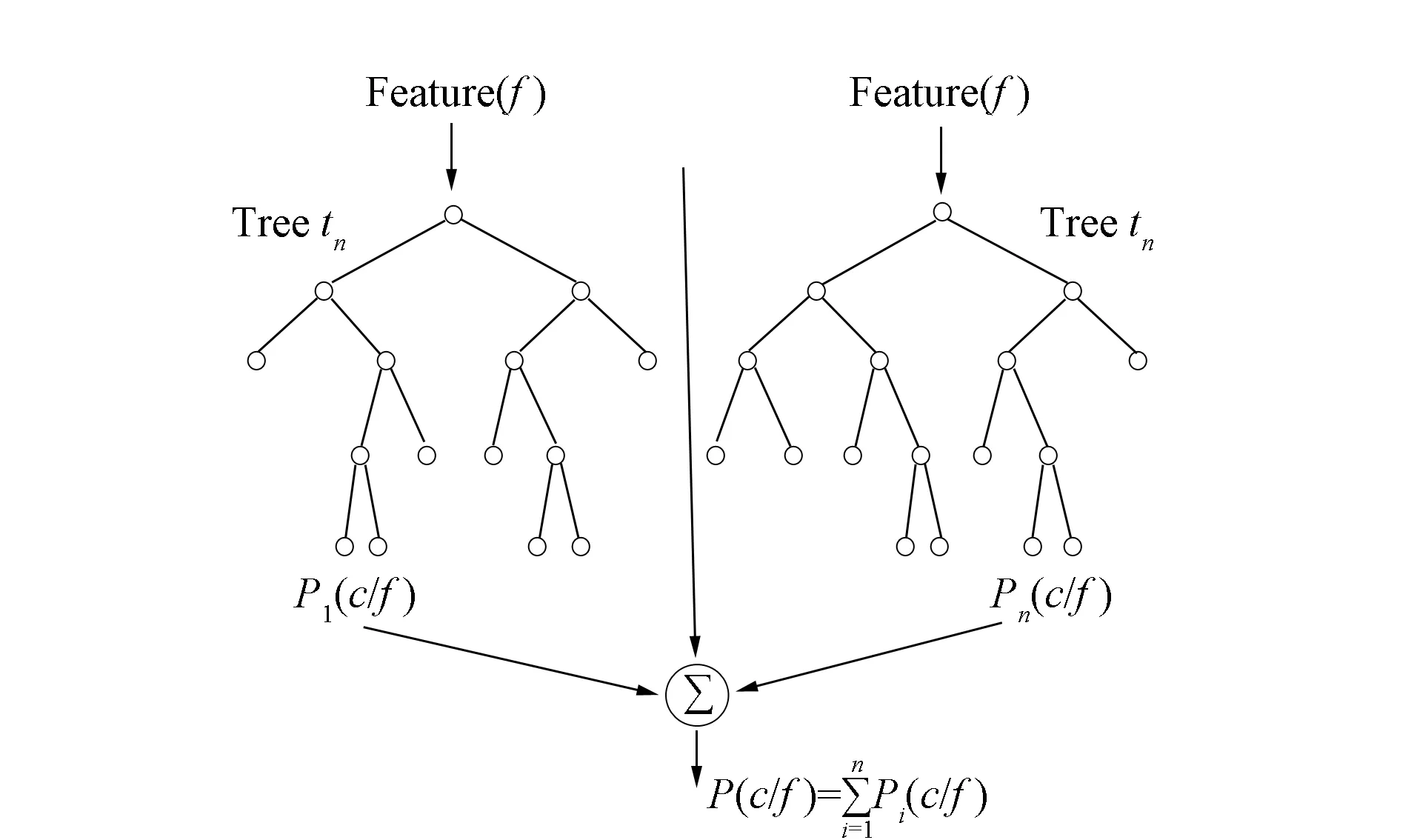
图1 随机森林模型Fig.1 Model of random forest

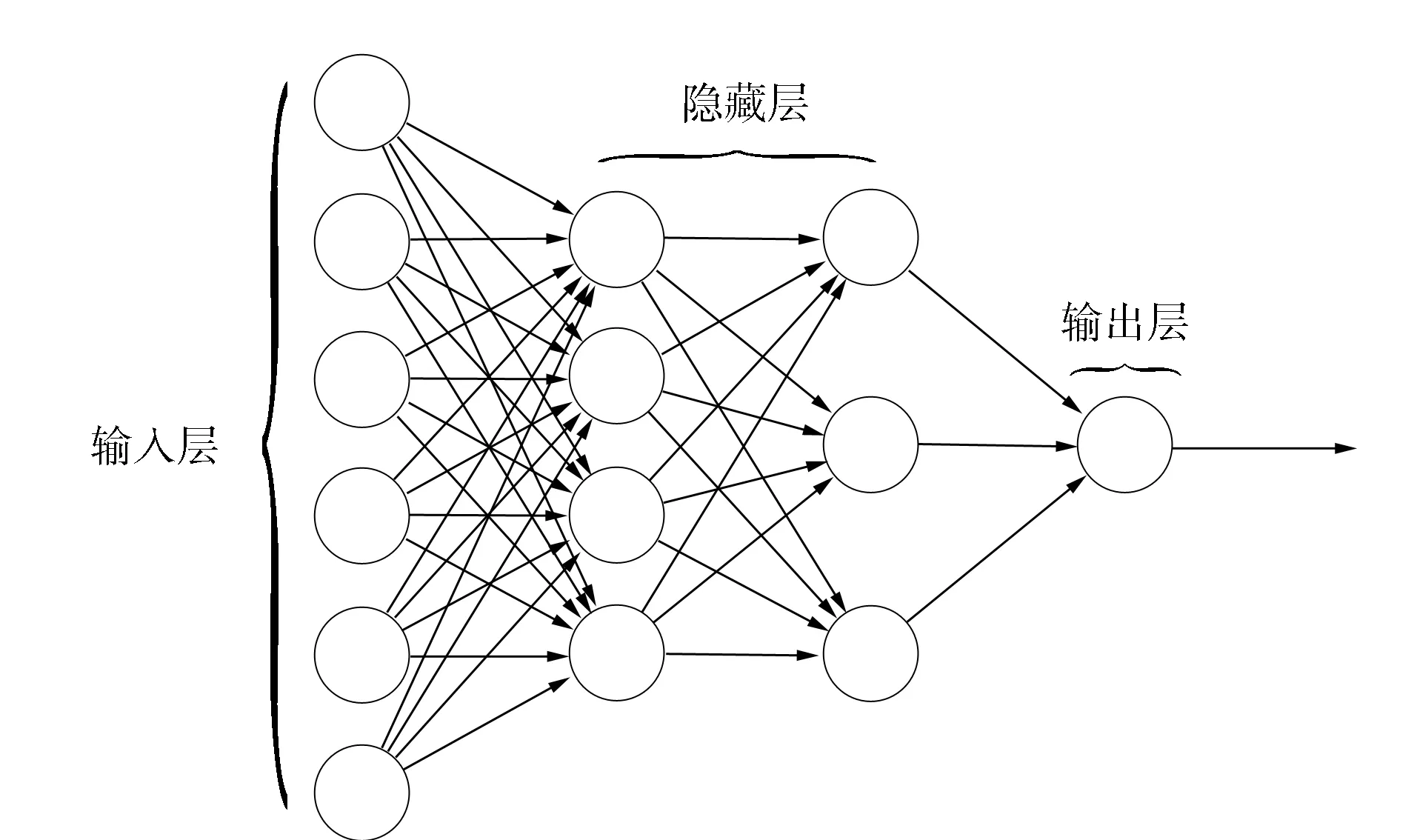
图2 MLP模型Fig.2 Model of MLP

一般的多层全连接神经网络(如MLP)是一种前向结构的人工智能网络. 如图2所示,典型的MLP包括三层：输入层、隐藏层和输出层,MLP神经网络不同层之间是全连接的. 多层全连接神经网络的每一层都由多个节点组成. 除输入层的节点外,每个神经元都带有一个非线性激活函数,通常用反向传播的监督学习方法训练网络[9].

假设输入层用向量X表示,则隐藏层的输出为f(W1X+b1),其中W1是权重(也称为连接系数),b1是偏置,函数f可以是常用的Sigmoid函数或tanh函数,其公式为

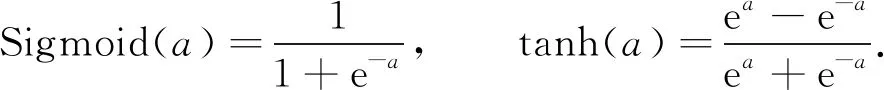
(1)

MLP回归模型的隐藏层到输出层可视为一个多类别的逻辑回归,即Softmax回归,所以输出层的输出就是Softmax(W2X1+B2),其中X1表示隐藏层的输出f(W1X+b1)[10-11]. Softmax公式为

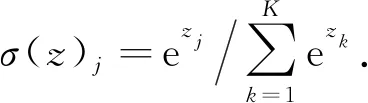
(2)

当在二分类问题上使用Softmax回归时,Softmax即特殊化成了Sigmoid.

2 优化的MLP回归模型

本文提出的优化MLP回归模型流程包括：数据集预处理、数据集分组、建立神经网络模型、获得不确定项以及完善预测结果.

1) 对数据集进行数据预处理. 由于在实际应用中获得的数据多数包含噪声,所以不能将这种数据直接进行数据分析. 为提高数据分析的效率,通常采用数据预处理技术进行数据预处理. 数据预处理有多种方法：数据清洗、数据集成、数据变换等,这些处理方法都可以在一定程度上降低数据分析的成本[12].

2) 根据数据的不同属性,将处理后的数据集按数据属性分为两组数据子集S和Z. 将这两组数据子集定义如下:

S={S1,S2,…,Sn},Si∈[0,1],i∈{1,2,…,n};

Z={Z1,Z2,…,Zn},Zi∈,i∈{1,2,…,n}.

3) 建立模型. 首先用MLP回归模型分析数据集S,并进行训练获得MLP的输出,用随机森林算法预测数据集Z. 将MLP回归模型以及随机森林算法的输出分别记为mlp_predict和forest_predict.

4) 提取不确定项. 得到随机森林的输出后,即可通过对比它们之间的不同输出获得不确定项(当它们对同一个数据项的预测有不同意见时,称该项为不确定项). 如果要得到更高的预测准确率,则需使不确定项最大化. 不确定项提取算法描述如下：

算法1不确定项提取算法.

输入: forest_predict(随机森林算法的输出结果),mlp_predict(MLP层获得的输出结果),y_test(结果集);

输出: DataFrame类型的不确定项集合;

初始化f_m_index(随机森林算法和MLP层的差异项索引)

fm_t_index(随机森林算法或MLP层与y_test的差异项索引)

f_m_diff(随机森林算法和MLP层的差异错误项索引)=[ ],[ ],[ ]

for index∈[0: len(forest_predict[0])] do:

当随机森林算法和MLP层得到的结果不同时

将index记录到f_m_index中

end for

for index∈[0: len(forest_predict或者mlp_predict [0])] do:

如果随机森林算法或者MLP层得到的是错误结果

将index记录到fm_t_index中

end for

for index∈[0: len(f_m_index)] do:

forf_m_index∈[0: len(fm_t_index)] do:

如果所针对的数据在差异项中并与实际不符

将index记录到f_m_diff中

break

end for

returnx_test中索引值为f_m_diff中元素的DataFrame类型的对象.

其中forest_predict和mlp_predict分别表示随机森林和MLP层的输出结果,在算法运行时选择其中正确率较高的输出.

5) 完善预测结果. 获取不确定项集合后,可将其传递给逻辑回归层,需要针对这些不确定项重新训练并更新MLP回归模型中的逻辑回归层参数. 用训练集中的不确定项拟合逻辑回归层,最后用该层预测测试集中的不确定项,再根据之前得到的输出结果得到最终的预测结果. 获得逻辑回归层的训练集过程与获取差异项的过程基本相同. 该神经网络模型结构如图3所示.

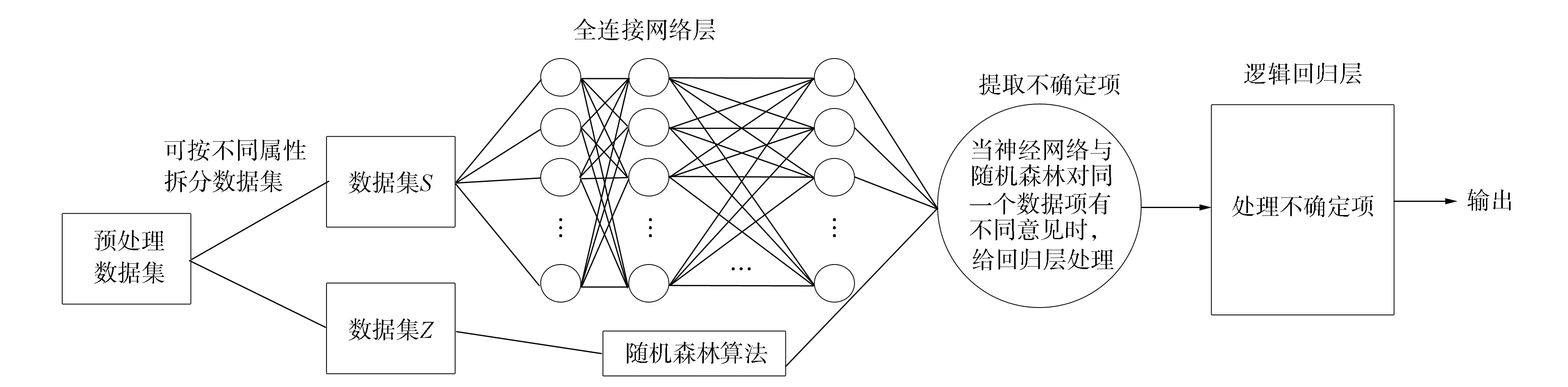
图3 随机森林优化的网络模型Fig.3 Network model for random forest optimization

由图3可见,本文提出的优化算法是在原MLP回归模型中的MLP层与逻辑回归层之间加入了不确定项的析出算法,并使用逻辑回归层处理这些不确定项. 对于MLP层或随机森林的隐藏层状态,用Sigmoid激活函数获得其对应的输出结果,最后用逻辑回归层的结果完善MLP层或随机森林算法的输出结果.

Sigmoid二分类算法本质上是一个基于条件概率的判别模型,通常以0.5为阈值,大于0.5为正样本,小于0.5为负样本,是一个二分类方法. 将Sigmoid回归函数扩展到多维特征空间,即为多维特征空间中的二分类问题[13-14]. 在多维特征空间中的Sigmoid函数公式为

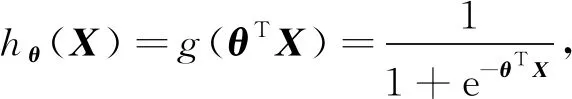
(3)

其中θ表示多维参数,X为特征空间矩阵. 对于二分类问题,样本和参数θ的条件概率函数公式为

P(y|X;θ)=(hθ(X))y(1-hθ(X))1-y,

(4)

其中y表示二分类问题输出. 得到概率函数后,对其进行最大似然估计并对数化,公式如下：

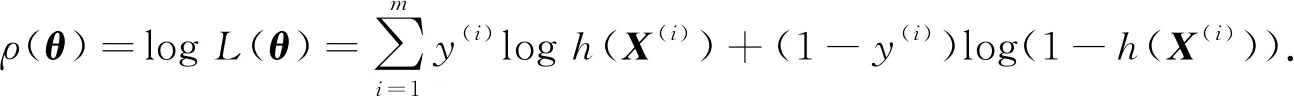
(5)

对式(5)求参数θ的导数,得到参数梯度迭代公式为

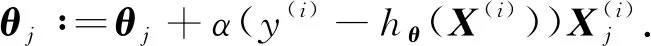
(6)

通过在训练集上的不断迭代,得到导数的近似极值,该过程称为梯度上升,最后获得最佳参数θ和可用模型.

3 实 验

3.1 数据集

表1为2013年和2017年贷款客户数据集,其取自于lend club借贷网站(https://www.lendingclub.com/info/download-data.action)中的贷款客户信息,其中包含客户的静态信息(如收入、工作、家庭条件等)和动态信息(客户的历史信用等).

表1 2013年和2017年贷款客户数据集

本文主要使用该数据集中的loan_amnt,funded_amnt等属性进行随机森林的初次预测,而home_own,desc等属性作为多层感知机初次预测的属性. 由于数据量过大,本文截取了2013年和2017年的数据进行分析,其中LoanStats3a数据集样本数量为42 540个,属性数量为135个,LoanStats_2017Q1数据集样本数量为42 536个,属性数量为66个.

3.2 数据初始化

先用多种数据预处理算法,去除数据的冗余属性,降低特征数量,然后分析数据集中各项属性的相关性,去除分析结果中低的正相关性和负相关性特征(即移除冗余特征),填充与结果相关的残缺属性值. 获得可用的数据集后,对该数据集进行多种算法测试,考察其性能及进行特征提取前后对测试结果的影响,获得的数据结果将作为调整该模型结构的理论依据.

通过下列过程完成对初始数据的预处理：

1) 用统计属性中相同项个数确定是否是唯一属性,删除数据集中的唯一属性,如id,member_id和sub_grade等属性;

2) 处理数据集中的非数值数据,去除int_rate中的“%”,只保留其数值部分并转换成float类型；将loan_status属性中的“fully paid”全部用1代替,“charged off”全部用0代替,其他字段全部用Nan代替；将数据集中“n/a”全部使用Nan值替换,然后删除loan_status属性中为Nan的样本,因为loan_status作为结果集,不允许其值为Nan;

3) 删除数据集中为Nan的属性或样本;

4) 处理数据项中数据类型为object,int,float属性的残缺值,若数据项中的值为0,Nan为空即为缺失项,缺失率(缺失项占总体的百分数)计算公式为

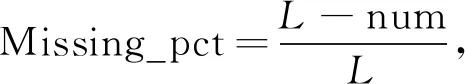
(7)

其中L表示目标属性的长度,num表示目标属性为0的个数；

5) 经过上述对数据的清洗后,计算数据集属性间的线性相关系数,公式为

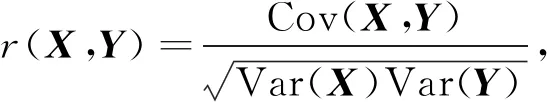
(8)

其中Cov(X,Y)表示X与Y的协方差,Var(X)表示X的方差,Var(Y)表示Y的方差,X和Y是输入的属性特征,最后只保留|r(X,Y)|>0.7,r(X,Y)∈[0,1]的属性; 由式(8)得到一个n×n维的下三角相关性系数矩阵,其中n为数据集属性个数.

6) 填充缺失的数据,数值型或自定义类型的属性填充均值或1,object类型的属性在本属性的定义域中随机选择.

经过处理后可得两个数据集feature1.csv和feature2.csv,其信息列于表2.

表2 预处理后的数据集信息

该模型将数据集按属性分为两组(集合S和Z),实验观察不同算法在数据集Z上的性能,统计其在该数据集中可获得不确定项集合的大小,选择其中最佳的搭配方案. 完成上述工作后,提取出之前在训练集上的不确定项进行训练,更新MLP回归模型的逻辑回归层参数.

3.3 实验分析

构建该模型前,先单独分析了MLP、随机森林、逻辑回归交叉验证(CLF)和逻辑回归(LR)算法在feature1数据集上的性能,因为这些结果有助于更好地调整该模型的结构和参数,最后选择其中一个对MLP回归模型进行优化. 在实验分析中会在数据预处理后加入PCA算法进行对比. 数据统计结果表明,CLF算法和PCA算法对其他算法的最终预测结果具有反作用,所以可考虑在实验中去掉该流程. 上述各算法在训练集、测试集及带有PCA过程的测试集上进行10次预测结果的平均F1值列于表3. 由表3可见,各算法数据之间的差别不明显,所以本文以图的形式(图4)显示它们之间的区别,为增加数据之间的差距,图4中只显示F1值超过0.8的部分.

表3 不同算法在训练集和测试集上的预测平均F1值

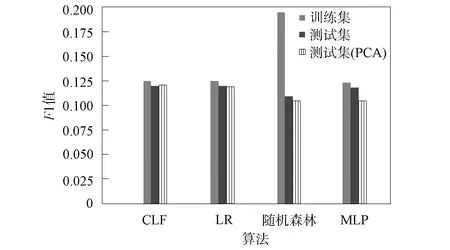
图4 不同算法的平均预测F1值Fig.4 Average prediction F1 value of different algorithms

优化的MLP回归模型进行隐藏层状态纠正要用两种异构算法,在MLP回归模型中,MLP层是经典的神经网络结构,其主要解决分类和预测相关的问题,在本文模型中仍使用MLP层处理数据集S,探索另外一个能与MLP层搭配的其他算法. 对数值型数据集的分析,按无特征提取算法的性能,应采取性能较好的逻辑回归算法. 但在测试中发现,MLP层搭配逻辑回归算法的结构不能获得足够的不确定项,导致无法析出更多的错误以便于纠错(不确定项集合中几乎都是错误项),所以将对处理数据集Z的算法修改为随机森林算法,以得到更大的不确定项集合,因此,MLP层搭配随机森林算法的结构得到的不确定项最多.

实验中发现,使用逻辑回归层的两个条件概率都服从Laplace分布,所以penalty设为l1. 参数C为正则化系数的倒数,表示正则化的程度,纠错模型使用的数据集,样本规模小、随机因素大,导致其正则化程度小,所以参数C应设为1；参数fit_intercept表示是否存在截距或偏差,通常设为true；迭代次数max_iter设为100,其值越大,代价函数收敛程度越高. 模型中MLP层的参数设置如下：隐藏层设为100×200×100,激活函数为ReLU. 图5为ReLU,Sigmoid和tanh函数的曲线. 优化器使用L-BFGS,实验使用的数据集有较多的属性数量,在每次迭代时都要存储近似Hesse矩阵,占用了过多的存储空间,降低了算法效率. L-BFGS算法是BFGS算法的一种改进算法,其只保存最近的m次迭代信息,以降低数据的存储空间,提高算法效率. 使用该优化器训练输入层和输出层的权重和偏置.

经过上述过程,对不确定项的预测即具备了实现的前提条件. 本文引入两个对比模型: 模型1为使用原MLP回归模型中已经训练好的逻辑回归层参数对其进行预测,试验结果表明,预测结果并不理想,准确率多数达不到20%；模型2为将所有训练集中的不确定项作为逻辑回归层的训练集训练并更新逻辑回归层的参数,实验结果表明,参数更新后的逻辑回归层具有良好的预测结果. 图6为上述两个模型的纠错结果对比.

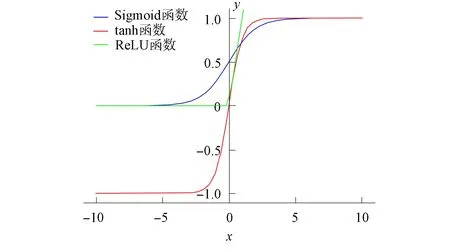
图5 ReLU,Sigmoid和tanh函数曲线Fig.5 Function curves of ReLU,Sigmoid and tanh

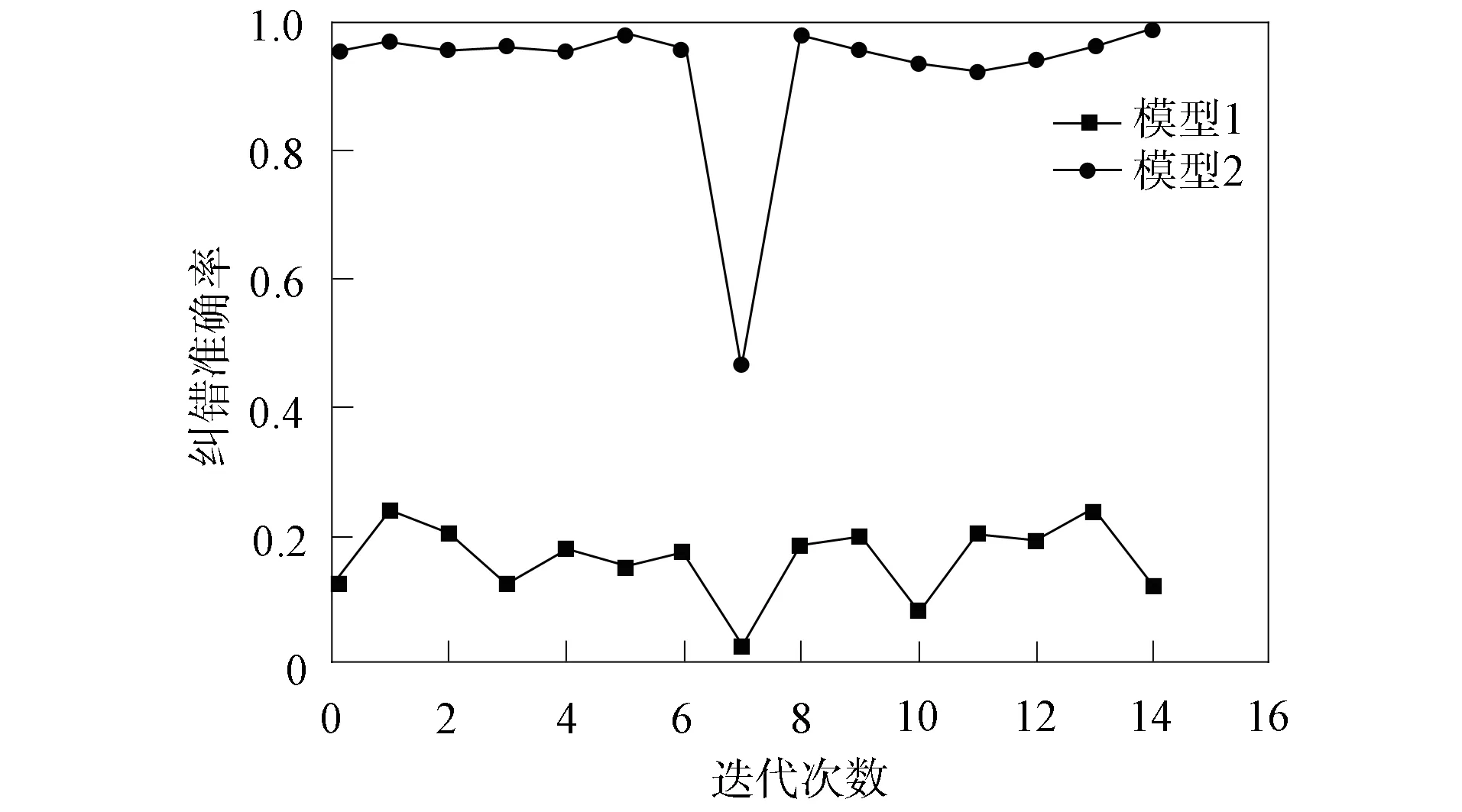
图6 模型1和模型2纠错结果对比Fig.6 Comparison of error correction results of model 1 and model 2

图7为实验的最终结果. 选择实验数据集feature2进行预测,与数据集feature1相比,该数据集有更少的数据属性,对这两个数据集相同部分的预处理使用对feature1数据集的处理方法,只保留feature1数据集实验中用到的属性.

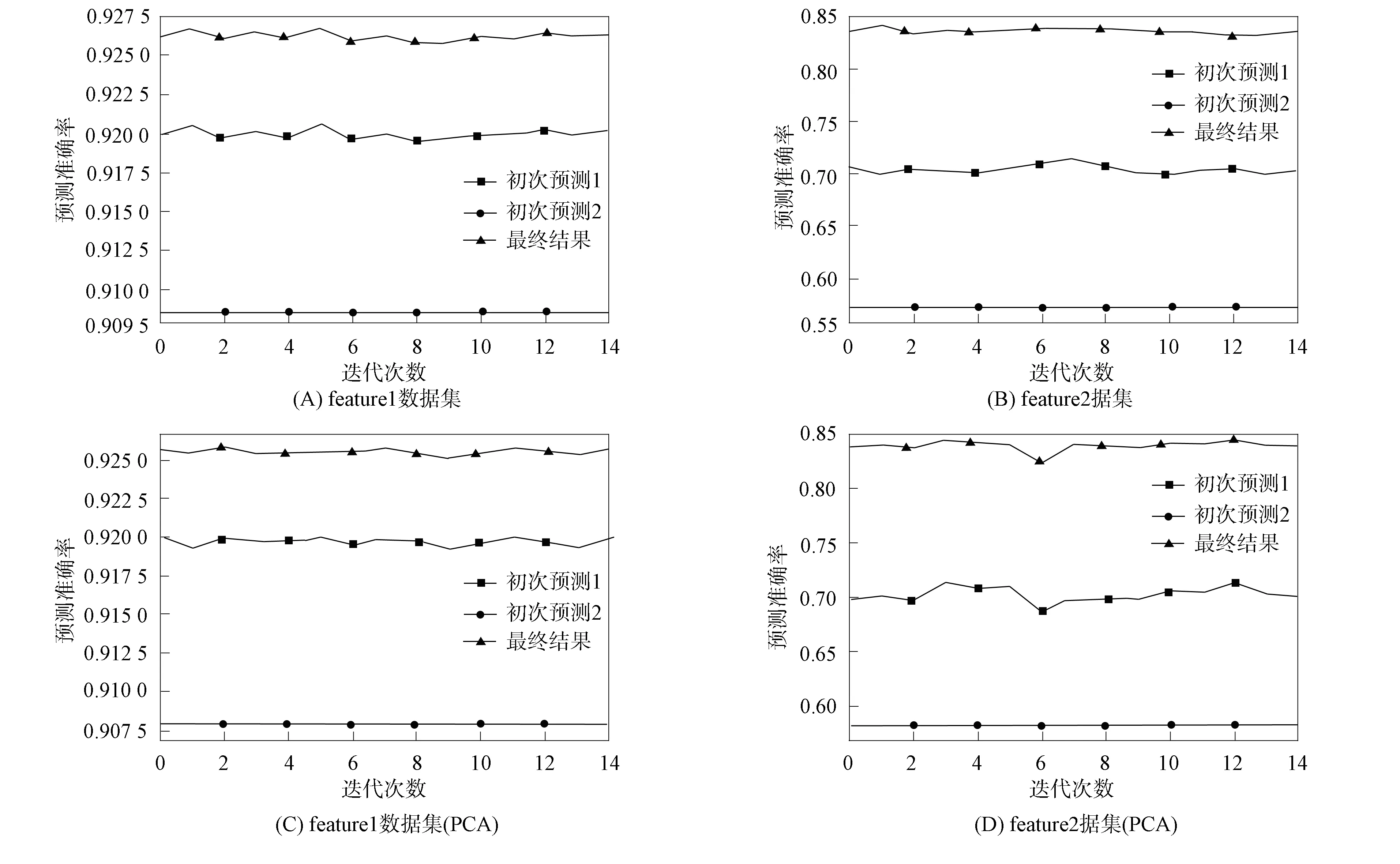
图7 不同数据集上本文算法的实验结果Fig.7 Experimental results of proposed algorithm on different data sets

在使用feature2数据集的实验中发现,如果只使用传统预测方法将获得比初次实验更低的预测率,这是因为数据集维度的降低导致算法不能更大范围地提取影响实验结果. 但在获取不确定项过程中却性能更好,每次测试都会得到很多不确定项,从而有利于纠正大量的错误,纠错率较好. 对于不在不确定项中的错误预测结果,多是来源于采集数据的自身误差或是数据集外的因素,其不属于因为数据集特征属性残缺带来的预测误差. 导致这些错误的因素较复杂,对其纠正存在更高的难度,相对于整个算法的成本不再具有更高的预测价值.

经过一系列的结构调整和局部算法的参数修改,得到最终的模型结构. 该模型总体的实验结果表明,在多种实验数据集中,该算法总能较好地提高最终预测效率. 一般情况下,特征完整的数据集与非特征完整的数据集相比,获得的不确定项数目较少. 在实际数据挖掘中,采集的数据总会存在或多或少的残缺和误差,从而给不确定项的获取提供了条件,所以可证明析出不确定项并对其进行改进的思路可行(在不同的应用领域或数据集表现有差别). 图7是对该模型在feature1和feature2数据集上进行15次测试得到的最终结果(包括预处理后使用PCA重要特征提取算法),在产生不确定项前对MLP层和随机森林算法的初次分类结果在图7中分别用初次预测1和初次预测2表示.

综上所述,相对基于特征降维的神经网络预测模型,本文优化模型能更全面地分析实际问题,获得更合理的预测结果. 本文模型的改进之处是MLP回归模型的逻辑回归层不再用于处理全连接层的输出状态,而是用于获取不确定项的预测结果,这些不确定项中包含了一般神经网络可能忽略的数据特征. 对于数据中显然的特征,都可被MLP回归模型的全连接层或随机森林算分析和处理,只需在输出位置连接一个Softmax或Sigmoid分类器即可获得分类结果. 在很多较复杂的分类问题中,因为大量的属性特征具有错综复杂的相关关系,很多神经网络模型未对其进行完整分析,因此通过某种方式划分数据集并独立分析是一种较好的方法.