光子的量子波动方程

刘 晗,杨涪铨,潘 庆,任明丽,郭义庆,吴向尧

(1. 吉林师范大学 物理学院,吉林 四平 136000；2. 中国科学院 高能物理研究所,北京 100049)

Maxwell方程组是描述光的宏观电磁理论,其满足相对论要求[1]. Dirac首先将电磁场量子化[2],量子化后的电磁场能量为一系列不连续的量,即

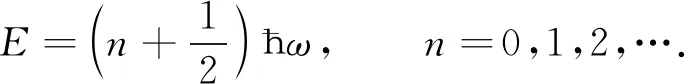
量子化结果表明,宏观电磁场由大量不连续的光子构成,电磁场的最低能量激发对应一个光子态,较高能量激发对应多个光子态. 因此量子化后的电磁场解释了光子的存在. 同时,量子理论认为所有粒子均具有波粒二象性. 文献[3-5]研究表明,由于光子作为相对论性粒子,不具有Schrödinger方程所描述非相对论粒子的波动特性,因此不存在光的波函数和几率密度. 其中,电子与光子间的关键区别在于光子的局域问题,电子可处于位置本征态,而光子不能处于位置本征态,但自由空间电磁场的能量密度可表示为一个局域量E2(x)+c2B2(x). 文献[6-13]通过定义光的波函数

ψ(r,t)=2-1/2(E(r,t)+iH(r,t))

给出了光子的波动方程.

本文给出外场中粒子的Lagrange函数及其Hamilton量的相对论表达式. 令静止质量m0=0,进一步给出光子的Hamilton量及光子在介质中的势能. 由于光子自旋s=1,为矢量粒子,因此其波函数为矢量函数. 在此基础上,通过理论推导给出自由和非自由光子的量子波动方程,用该方程可研究光在光子晶体中的量子色散关系及量子透射等特性.

1 光子的相对论Hamilton量

外场中粒子的Lagrange相对论表达式为

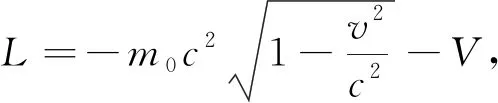
(1)

其中m0为粒子的静止质量,v为粒子速度,c为光速,V为粒子在外场中的势能. 由L可得正则动量p为

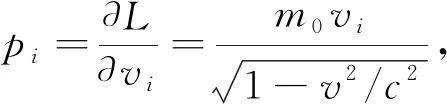
(2)

则

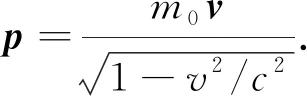
(3)

Hamilton量的表达式为

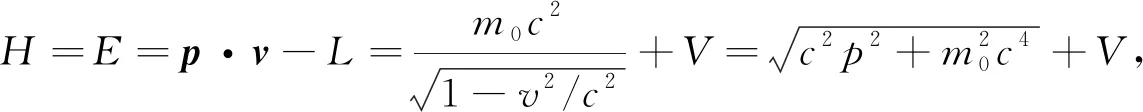
(4)

其中E为粒子的总能量. 对于光子,静止质量为m0=0,则式(4)变为

E=cp+V.

(5)

在介质中,光子的能量、动量和速度分别为

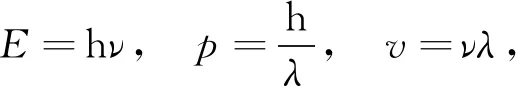
(6)

其中ν为光子频率,λ为光子波长. 将式(6)代入式(5)可得

hv=hc+Vλ,

(7)

由式(7)可得介质中光子的势能为

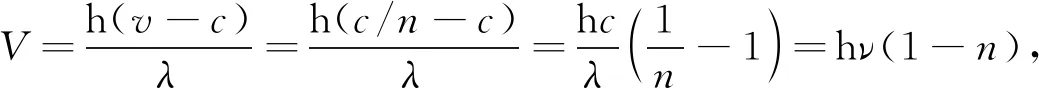
(8)

将式(8)代入式(5)可得介质中光子的能量为

E=cp+V=pv.

(9)

2 介质中光子的量子波方程

利用光子能量方程(5)可研究介质中光子的量子波动方程. 方程(5)可写为

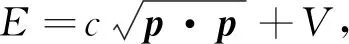
(10)

符合归一化条件的多分量波函数ψ(p,E)满足

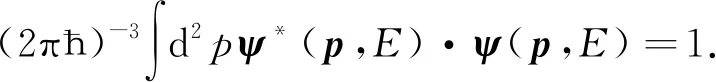
(11)

由于光子自旋s=1,因此其波函数有3个分量,ψ(p,E)=(ψx(p,E),ψy(p,E),ψz(p,E)),用波函数ψ(p,E)乘以方程(10)可得

(12)

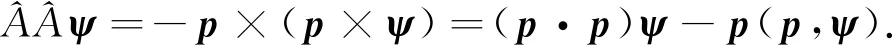
(13)

任何矢量场均可写为两个线性无关部分之和,即ψ=ψT+ψL,其中横向部分ψT和纵向部分ψL满足

p·ψT=0,p×ψL=0,

(14)

式(13)可写为

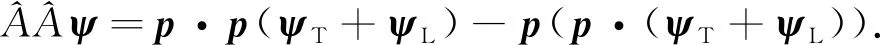
(15)

以横向部分ψT为光子的相关场,对于光子场ψT,将式(15)写为

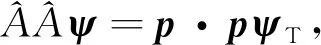
(16)

即

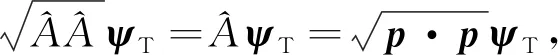
(17)

用光速c乘以式(17),将式(12)代入式(17)可得

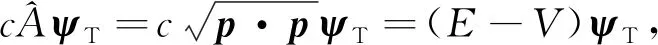
(18)

或

(E-V)ψT(p,E)=cip×ψT(p,E).

(19)

由式(19)知,ψT(p,E)为复矢量,将波函数ψ(p,E)做动量空间到坐标空间及能量到时间的Fourier变换,通过包含一个δ函数表示能量和动量间的约束(E=c|p|). 能量E为一个独立变量,可给出

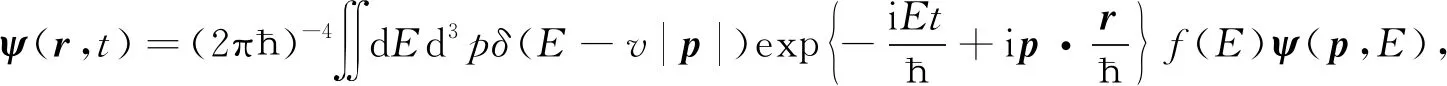
(20)

其中权函数f(E)可允许得到不同形式的归一化波函数ψ(r,t),对于光子,则有

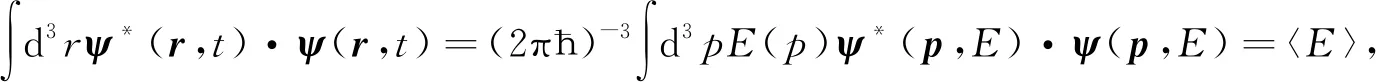
(21)

其中〈E〉表示光子能量的期望值. 对于光子波函数ψT(r,t),存在与ψ(r,t)相同的变换,即

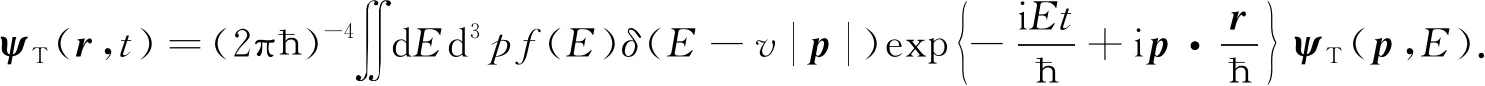
(22)

对式(22),有如下逆转Fourier变换:

同时有

将式(23)～(25)代入式(19)可得

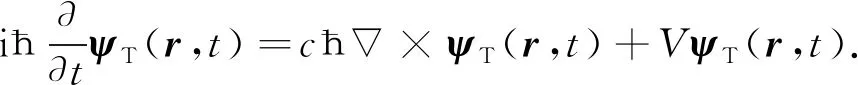
(26)

方程(26)为介质中光子的量子波动方程. 对于自由光子(V=0),有

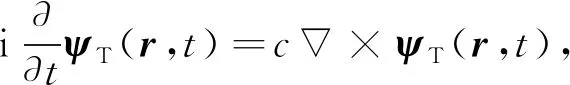
(27)

用方程(27)乘以ħ可得

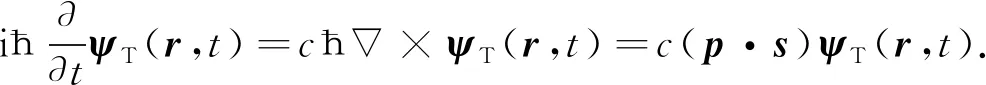
(28)

由

(29)

可得

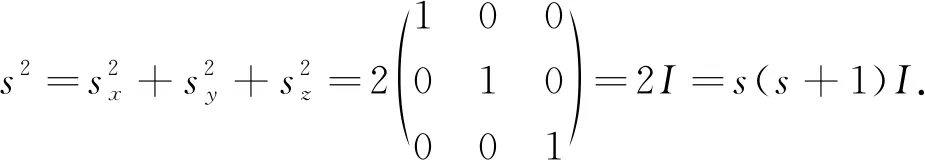
(30)

由方程(30)可得s=1. 因此方程(27)和方程(28)对应于自旋s=1,静止质量m0=0的粒子波动方程,即光子的量子波动方程.

3 光子量子波动方程的应用

下面给出光子量子波动方程的一些应用实例,其中包括研究光在一般介质和光子晶体中的量子性质. 由方程(26)通过分离变量法

ψ(r,t)=ψ(r)f(t)

(31)

可得

即

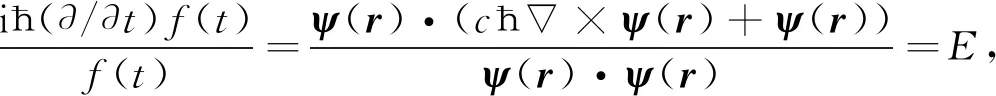
(32)

从而可得光子的能量本征方程

cħ×ψ(r)+ψ(r)=Eψ(r).

(33)

在折射率为n的介质中,光子势能为

V=ħω(1-n),

(34)

将方程(34)代入式(33)即可研究光在介质中的量子特性. 方程(26)的共轭方程为

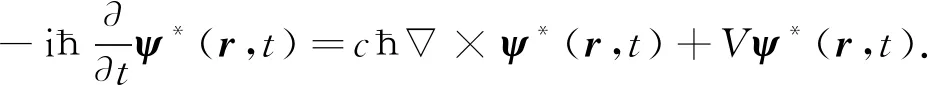
(35)

将方程(26)乘以ψ*与方程(35)乘以ψ后相减可得

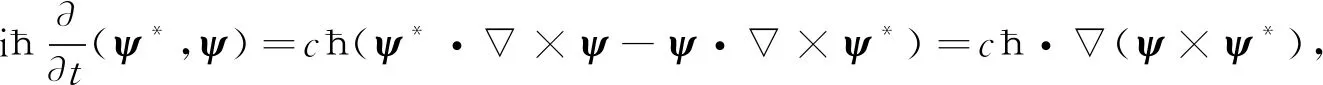
(36)

或

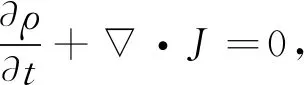
(37)

其中

ρ=ψ*·ψ,J=icψ×ψ*.

(38)

定义量子透射率T和反射率R分别为

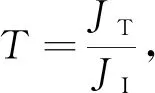
(39)

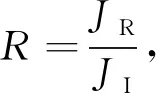
(40)

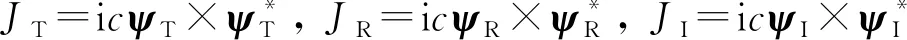
综上,本文给出了外场中粒子的Lagrange函数及其Hamilton量的相对论表达式. 令静止质量m0=0,进一步给出了光子的Hamilton量及光子在介质中的势能. 由于光子自旋s=1,为矢量粒子,因此其波函数为矢量函数. 在此基础上,通过理论推导给出了自由和非自由光子的量子波动方程,用该方程可研究光在光子晶体中的量子色散关系及量子透射等特性.